Что значит углы сонаправлены

Углы с сонаправленными сторонами

Урок 8. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Углы с сонаправленными сторонами»

· введем понятие сонаправленных лучей;

· дадим определение сонаправленных лучей;

· докажем теорему о равенстве углов с сонаправленными сторонами.

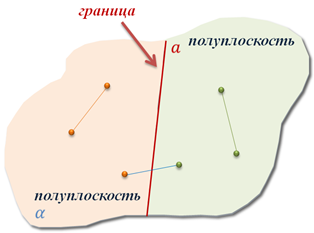
На этом уроке нам понадобится одна из аксиом планиметрии, которая звучит следующим образом: «любая прямая разбивает плоскость на две полуплоскости».

Итак, пусть у нас есть некоторая прямая а, которая лежит в плоскости α. Согласно аксиоме, эта прямая разделяет плоскость α на две части. Каждую из которой, называют полуплоскостью.

Понятно, что наша прямая а разделила плоскость α на две полуплоскости. Одна из которых лежит слева от прямой а, вторая – справа. В свою очередь, прямую а называют границей каждой из этих полуплоскостей.

Обратите внимание, любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а. А вот любые две точки разных полуплоскостей лежат по разные стороны от этой прямой.

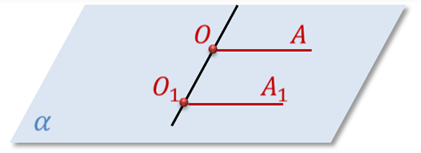
Определение. Два луча ОА и О₁А один в пространстве, не лежащие на одной прямой, называются сонаправленными (т.е. одинаково направленными), если они параллельны и лежат в одной полуплоскости с границей ОО₁.

Напомню, что два луча называются параллельными, если они лежат на параллельных прямых.

Лучи ОА и O₁A₁, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Докажем теорему об углах с сонаправленными сторонами.

Теорема. Если стороны двух углов соответственно сонаправленны, то такие углы равны.

Доказательство. Рассмотрим случай, когда углы О и О₁ с соответственно сонаправленными сторонами лежат в разных плоскостях.

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные лучи ОB и

О₁B₁. Т.е. мы имеем два угла АОB и А₁О₁B₁, стороны которых лежат на сонаправленных лучах. Докажем, что угол АОB равен углу А₁О₁B₁.

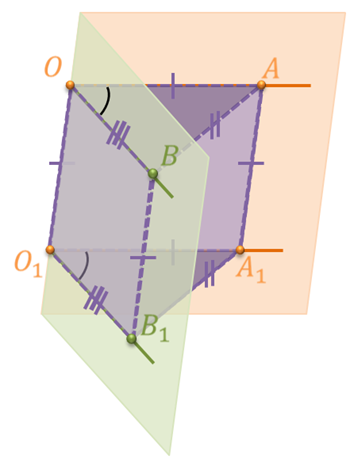
Отметим на сторонах лучей ОА и O₁A₁ точки А и A₁ так, чтобы отрезки ОА и O₁A₁ были равны. На сторонах лучей ОB и O₁B₁ отметим точки B и B₁ так, чтобы отрезки ОB и O₁B₁ были равны.

Рассмотрим четырехугольник ОАA₁O₁. Так как лучи ОА и O₁A₁ параллельны по условию (сонаправленны ) и равны по построению, то четырехугольник ОАА₁О₁ является параллелограммом по признаку параллелограмма. Следовательно, АА₁ параллельно ОО₁ и АА₁ равно ОО₁.

Рассмотрим четырехугольник ОBB₁O₁. Его стороны ОB и O₁B₁ параллельны, т.к. лежат на сонаправленных лучах по условию и равны по построению. Значит, по признаку параллелограмма четырехугольник OBB₁O₁ является параллелограммом. Тогда, стороны BB₁ и OO₁ параллельны и равны.

Обратите внимание, мы получили, что прямая AA₁ параллельна прямой OO₁ и прямая BB₁ параллельна прямой OO₁. Тогда по признаку параллельности прямых в пространстве, прямые AA₁ и BB₁ параллельны.

Рассмотрим четырехугольник BAA1B1. В этом четырехугольнике стороны AA₁ и BB₁ параллельны и равны. А значит, BAA₁B₁ – параллелограмм по признаку параллелограмма. Следовательно, стороны АB и A₁B₁ тоже параллельны и равны.

Теперь рассмотрим треугольники АОB и A₁O₁B₁. Стороны ОА и O₁A₁ равны по построению. Стороны ОB и O₁B₁ также равны по построению. Выше мы доказали, что стороны АB и A₁B₁ равны. Значит, треугольники АОB и A₁O₁B₁ равны по трем сторонам. Напомню, что в равных треугольниках против соответственно равных сторон лежат равные углы. Значит, углы АОB и A₁O₁B₁ равны. Теорема доказана.

Задание. Рассмотрите рисунок и

а) укажите лучи, которые являются сонаправленными;

б) укажите лучи, которые не являются сонаправленными.

Подведем итоги урока. На этом уроке мы ввели понятие сонаправленных лучей. Узнали, что два луча ОА и О один А один в пространстве, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной полуплоскости с границей О О один. Лучи ОА и О один А один, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой. А также доказали теорему о равенстве углов с сонаправленными сторонами.

Источник

2. Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми

Скрещивающиеся прямые

Нам известны два случая расположения прямых в пространстве a ∩ b; а || b. Общее для них: они лежат в одной плоскости (рис. 1, 2).

(по следствию из аксиомы)

(по определению параллельных прямых)

ЗАДАНИЕ №1 в рабочей тетради

Значит, в пространстве есть прямые, которые не пересекаются и не являются параллельными, так как они не лежат в одной плоскости. Такие прямые называются скрещивающимися.

Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости.

Теорема (признак скрещивающихся прямых)

Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, то эти прямые скрещивающиеся.

Дано: АВ ⊂ α, CD ∩ α = С, С ∉ АВ (рис. 4).

Доказать, что АВ скрещивается с CD.

Допустим, что CD и АВ лежит в одной плоскости. Пусть это будет плоскость β.

Плоскости совпадают, чего быть не может, так как прямая CD пересекает α. Плоскости, которой принадлежат АВ и CD не существует и следовательно по определению скрещивающихся прямых АВ скрещивается с CD.

ЗАДАНИЕ №2 в рабочей тетради

Теорема :

Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой плоскости, и притом только одна.

Доказательство: учащиеся разбирают по учебнику самостоятельно с последующей записью на доске и в тетрадях.

Дано: АВ скрещивается CD (рис. 6).

Построить α: АВ ⊂ α, CD || α.

1. Через точку А проведем прямую АЕ, АЕ || CD.

В доказательстве этой теоремы дается способ построения плоскости, проходящей через данную точку и параллельной двум скрещивающимся прямым. Рассмотреть задачу на построение.

Задание №3-№4 в рабочей тетради

Углы с сонаправленными сторонами. Угол между прямыми

Любая прямая а, лежащая в плоскости, разделяет плоскость на 2 части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей.

Источник

Конспект урока по теме «Угол с сонаправленными сторонами»

Геометрия,10 Дата 16.10.2017 Учитель: Чакал Э.М.

Угол с сонаправленными сторонами

1) ввести формулировку и доказательство теоремы о равенстве углов с ««направленными сторонами;

2) научится находить угол между прямыми в пространстве.

1. Организационный момент

2. Актуализация опорных знаний учащихся

а) Подготовить у доски доказательство признака скрещивающихся прямых.

б) Фронтальный теоретический опрос:

1. Верно ли утверждение: если две прямые не имеют общих точек, то они параллельны? (Нет.)

2. Две прямые параллельны некоторой плоскости. Могут ли эти прямые:

б) Быть скрещивающимися? (Да.)

3. Могут ли скрещивающиеся прямые а и b быть параллельными прямой с? (Нет.)

4. Даны две скрещивающиеся прямые а и b. Точки А и А1 лежат на прямой а, точки В и В1 лежат на прямой b. Как будут расположены прямые АВ и А1В1? (Ответ: АВ скрещивается с A1B1.)

6. Каково должно быть взаимное расположение трех прямых, чтобы можно провести плоскость, содержащую все прямые? (Прямые попарно пересекаются или две параллельны, а третья их пересекает.)

Проверка домашнего задания.

3. Изучение нового материала

Ввести понятие сонаправленных лучей и углов с сонаправленными сторонами.

Любая прямая а, лежащая в плоскости, разделяет плоскость на 2 части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей.

Два луча ОА и О1А1 (рис. 1), не лежащие на одной прямой, называются ««направленными, если они параллельны и лежат в одной плоскости с границей ОО1. Два луча ОА и О1А1, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

1. Найти сонаправленные лучи.

2. Указать лучи, которые не являются сонаправленными.

Если стороны двух углов соответственно сонаправлены, то такие углы равны.

Дано: ∠ O и ∠ О1 с сонаправленными сторонами (рис. 2).

Доказательство: На сторонах угла О отметим любые точки А и В и на соответственных сторонах угла О1 отметим точки А1 и В1 такие, что О1А1 = ОА и О1В1 = ОВ.

1. Рассмотрим ОАА1О1. — параллелограмм (по признаку). Значит, АА1 || ОО1 и АА1 = ОО1.

2. Рассмотрим ОВВ1О1. — параллелограмм (по признаку). Значит, ВВ1 || ОО1 и ВВ1 = ОО1.

3. Рассмотрим ΔАВО и ΔA1B1O1. ΔАВО = ΔА1В1О1 (по трем сторонам).

Ввести определение угла между пересекающимися прямыми.

Угол между скрещивающимися прямыми АВ и CD определяется как угол между пересекающимися прямыми А1В1 и C1D1 соответственно параллельными АВ и CD (рис. 3).

Зависит ли величина угла φ от выбора точки М1?

Выбрать (отметим) любую точку М2 и построить А2В2 || АВ и C2D2 || CD.

Ответить на вопросы:

1. Почему А2В2 || A1B1 и C2D21 || C1D1? (По теореме о трех параллельных прямых.)

2. Являются ли углы ∠ A1M1D1 и ∠ A2M2D2 углами с соответственно параллельными сторонами? (Да.)

1) ∠ A1M1B1 = ∠ A2M2B2 (по изученной теореме).

2) Величина угла между скрещивающимися прямыми не зависит от выбора точки.

4. Закрепление изученного материала

1. Устно. Дан куб ABCDA1B1C1D1 (рис. 4).

Найдите угол между прямыми. 1) ВС и СС1 (90°); 2) АС и ВС(45°); 3) D1C1 и ВС(90°). 4) А1В1 и АС(45°).

2. Задача № 44 (на доске и в тетрадях).

Дано: OB || CD; OA и CD скрещиваются;

a) ∠ AOB = 40°; б) ∠ AOB = 135°; в) ∠ AOB = 90° (рис. 5).

Найти: угол между ОА и CD.

a) ∠ AOB = 40°; CD || ОВ, то угол между скрещивающимися прямыми ОА и CD равен 40°.

б) ∠ АОВ = 135°. Угол между пересекающимися прямыми ОА и ОВ равен: 180°- 135° = 45°. Угол между скрещивающимися прямыми ОА и CD равен 45°.

в) ∠ АОВ = 90°. Угол между скрещивающимися прямыми ОА и CD равен 90°. (Ответ: а) 40°; б) 45°; в) 90°.)

3. Дополнительная задача

Определить: взаимное расположение прямых РК и АВ угол между РК и АВ.

1. АВ ∩ (ADC) = А; А ∉ РК, так как РК || АС (по свойству средней линии треугольника) ⇒ АВ и РК скрещиваются.

3. Угол между скрещивающимися прямыми равен 60°. (Ответ: АВ и РК скрещиваются; 60°.)

5. Подведение итогов урока

7.Домашнее задание П. 8; 9 № 40; 42.

Сегодня на уроке было интересно ___________________________________

Сегодня на уроке я научился _______________________________________

Сегодня на уроке мне показалось важным ____________________________.

Дать указание: повторить свойство четырехугольников, описанных около окружности.

№ 40. Дано: а скрещиваются b; (рис. 7).

Определить:

а) а ⊂ α, так как а скрещиваются b, то b ⊄ α.

б)

Определить: взаимное расположение CD и ЕК.

а) ЕК || АВ (по определению трапеции) ⇒ ЕК || CD (по теореме о трех параллельных прямых. CD || АВ (по определению параллелограмма);

б) АВ + ЕК = АЕ + ВК (по свойству четырехугольников, описанных около окружности). РABEK = АВ + ЕК + АЕ + ВК = 2 · (АВ + ЕК) = 2 · (22,5 + 27,5) = 100 (см). (Ответ: ЕК || CD; 100 см.)

Источник

Презентация по геометрии на тему «Углы с сонаправленными сторонами»

Описание презентации по отдельным слайдам:

Скрещивающиеся прямые. Углы с сонаправленными сторонами. Угол между прямыми.

Цели Образоватедьная Ввести формулировку и доказательство теоремы о равенстве углов с сонаправленными сторонами; научить находить угол между прямыми в пространстве. Развивающая Развивать у учащихся умение сравнивать и находить аналогии. Воспитательная Воспитывать самостоятельность, творческое отношение к учебному процессу

Расположение 2-х прямых на плоскости а║b пересекаются параллельны a b a b

Ответьте на вопросы по чертежу: Являются ли параллельными прямые АА1 и DD1; АА1 и CC1, и почему? Каково взаимное расположение прямых AA1 и DС?

Скрещивающиеся прямые скрещивающиеся Определение: Две прямые называются скрещивающимися, если они не лежат в одной плоскости (т.е. не существует плоскости, содержащей эти прямые). a b

Признак скрещивающихся прямых Если одна из двух прямых лежит в некоторой плоскости, а другая прямая пересекает эту плоскость в точке, не лежащей на первой прямой, эти прямые скрещивающиеся. Дано: Доказать: A B D C

Признак скрещивающихся прямых Доказательство: Пусть CD и АВ лежат в одной плоскости β. Тогда Плоскости совпадают, но по условию прямая CD пересекает α. Следовательно, плоскости β не существует и прямые АВ и CD скрещиваются. Дано: Доказать: A B B D C

Ответьте на вопросы по чертежу: Каково взаимное расположение прямых AB1 и DС; прямой DС и плоскости AА1 B1В; прямой AB1 и плоскости DD1 C1C?

Задача № 39 Дано: Доказать: Доказательство: 1) Єα по аксиоме А1 2) В¢α, так как по определению скрещивающихся прямых 3) по признаку скр.прямых

полуплоскость полуплоскость граница Любая прямая а, лежащая в плоскости, разделяет эту плоскость на две части, называемые полуплоскостями. Прямая а называется границей каждой из этих полуплоскостей. а

Сонаправленные лучи Два луча ОА иО1А1, не лежащие на одной прямой, называются сонаправленными, если они параллельны и лежат в одной плоскости с границей ОО1. Два луча ОА иО1А1, лежащие на одной прямой, называются сонаправленными, если они совпадают или один из них содержит другой.

Углы с сонаправленными сторонами A О О1 О2 A1 В2 A2 О3 A3

Если стороны двух углов соответственно сонаправлены, то такие углы равны. Теорема об углах с сонаправленными сторонами

Угол между скрещивающимися прямыми Угол между прямыми – это градусная мера, а не геометрическая фигура. Угол между скрещивающимися прямыми АВ и CD определяется как угол между пересекающимися прямыми А1В1║АВ и C1D1║CD (от выбора точки М1 или М2 величина угла φ не зависит)

Ответьте на вопросы по чертежу: Найдите угол между прямыми ВС и СС1 АС и ВС D1C1 и ВС А1В1 и АС

Задача № 44 Дано: ОВ║CD; а) ﮮАОВ=40º б) ﮮАОВ=135º в) ﮮАОВ=90º Найти: угол между ОА и CD

Подготовка к ЕГЭ Решение задач типа В 6

Домашнее задание п.7-9 № 37 № 40 № 93

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-475301

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

При детском омбудсмене в России создадут платформу для взаимодействия с родителями

Время чтения: 2 минуты

Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»

Время чтения: 1 минута

В России утвердили новый порядок формирования федерального перечня учебников

Время чтения: 1 минута

При засыпании человеческий мозг может решать сложные задачи

Время чтения: 1 минута

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Минпросвещения рассказали о формате обучения школьников после праздников

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Определение сонаправленных лучей.

Тема: « Углы и расстояние в пространстве ».

1. Скрещивающиеся прямые. Теоремы о скрещивающихся прямых.

2. Углы с сонаправленными сторонами.

3. Угол между прямыми.

Скрещивающиеся прямые.

Определение. Две прямые в пространстве называются скрещивающимися, если они не лежат в одной плоскости.

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Две прямые, имеющие лишь одну общую точку, называются пересекающимися.

Итак, возможны три случая взаимного расположения двух прямых в пространстве:

1) прямые пересекаются, т.е. имеют только одну общую точку;

2) прямые параллельны, т.е. лежат в одной плоскости и не пересекаются;

3) прямые скрещиваются, т.е. не лежат в одной плоскости.

AB⊂α, CD α=C, C ∉ AB

Доказать: AB скрещивается с DC

Доказательство.

Доказательство будем вести методом от противного.

Допустим, АВ и CD лежат в некоторой плоскости β.

Тогда плоскость β проходит через прямую AB и точку C.

Через прямую AB и не лежащую на ней точку C можно провести плоскость, и притом только одну (следствие из аксиом).Следовательно, β≡α.

Но это невозможно, т.к. прямая CD пересекает α. Пришли к противоречию, ⇒ AB и CD лежат в разных плоскостях (скрещиваются). Теорема доказана.

Теорема 2.Через каждую из двух скрещивающихся прямых проходит плоскость, параллельная другой прямой, и притом только одна.

Дано: АВ и CD – скрещивающиеся прямые.

Доказать: ∃ α: AB ⊂α, CD∥α

Доказательство.

2) Проведем плоскость α через пересекающиеся прямые AE и CD.

3) CD ∥ AE, AE ⊂ α ⇒ CD ∥ α.

Любая другая плоскость будет пересекать AB, а значит и параллельную ей прямую CD. Поэтому α – единственная. Теорема доказана

2. Углы с сонаправленными сторонами.

Определение сонаправленных лучей.

Любая прямая, например ОО₁, рассекает плоскость на две

полуплоскости. Если лучи ОА и О₁А₁ параллельны и лежат

в одной полуплоскости, то они называются сонаправленными.

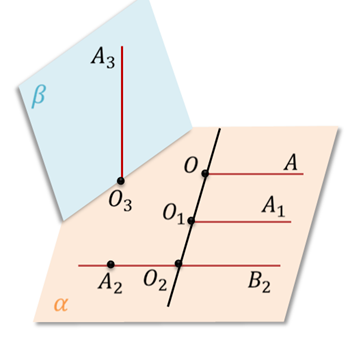
Лучи О₂А₂ и ОА не являются сонаправленными. Они параллельны, но не лежат в одной полуплоскости.

Теорема о равенстве углов с сонаправленными сторонами.Если стороны двух углов соответственно сонаправлены, то такие углы равны.

Пусть нам даны параллельные лучи ОА и О₁А₁ и параллельные

стороны лежат на сонаправленных лучах. Докажем, что эти

На стороне луча ОА и О₁А₁ выберем точки А и А₁так, чтобы отрезки ОА и О₁А₁ были равны. Аналогично, точки В и В₁ выберем так, чтобы отрезки ОВ и О₁В₁ были равны. Рассмотрим четырехугольник А₁О₁ОА. В этом четырехугольнике стороны ОА и О₁А₁ параллельны и равны. По признаку параллелограмма, четырехугольник А₁О₁ОА является параллелограммом. Так как А₁О₁ОА – параллелограмм, то стороны ОО₁ и АА₁ параллельны и равны.

Рассмотрим четырехугольник В₁О₁ОВ. В этом четырехугольнике

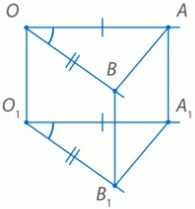
стороны ОВ и О₁В₁ параллельны и равны. По признаку

параллелограмма, четырехугольник В₁О₁ОВ является

параллелограммом. Так как В₁О₁ОВ – параллелограмм, то

стороны ОО1 и ВВ₁ параллельны и равны.

Рассмотрим четырехугольник В₁А₁АВ. В этом четырехугольнике стороны АА₁ и ВВ₁ параллельны и равны. По признаку параллелограмма, четырехугольник В₁А₁АВ является параллелограммом. Так как В₁А₁АВ – параллелограмм, то стороны АВ иА₁В₁ параллельны и равны.

Рассмотрим треугольники АОВ и А₁О₁В₁. Стороны ОА и О₁А₁ равны по построению. Стороны ОВ и О₁В₁ также равны по построению. А как мы доказали, и стороны АВ и А₁В₁ тоже равны. Значит, треугольники АОВ и А₁О₁В₁ равны по трем сторонам. В равных треугольниках против равных сторон лежат равные углы. Значит, углы АОВ и А₁О₁В₁ равны, что и требовалось доказать.

Угол между прямыми.

6.1 Угол между пересекающимися прямыми.

Если прямые пересекающиеся, то мы имеем четыре разных угла.

Углом между двумя прямыми, называется наименьший

из углов между двумя прямыми.

Угол между пересекающимися прямыми а и b обозначим α. Угол α такой, что .

6.2 Угол между скрещивающимися прямыми.

Пусть прямые а и b скрещивающиеся. Выберем произвольную точку О. Через точку О проведем прямую , параллельную прямой а, и прямую , параллельную прямой b. Прямые и пересекаются в точке О. Угол между двумя пересекающимися прямыми и , угол φ, и называется углом между скрещивающимися прямыми.

Решение задач.

Задача 1. Точка D не лежит в плоскости треугольника ABC, точки M, N, и P – середины отрезков DA, DB, и DC соответственно, точка K лежит на отрезке BN. Выясните взаимное расположение прямых:

а) ND и AB; б) PK и BC;

в) MN и AB; г) MP и AC;

д) NK и AC; е) MD и BC.

а) ND ∩ AB = B, поскольку N лежит между B и D;

б) PK пересекается с BC, поскольку PK не является средней линией BCD и поэтому не параллельна BC (PK ∩ BC = P1).

в) MN параллельна AB, т.к. MN – средняя линия ABD. Средняя линия треугольника параллельна основанию (MN AB).

г) MP параллельна AC, т.к. MP – средняя линия ACD (MP AC);

д) NK и AC скрещивающиеся, т.к. они не принадлежат одной плоскости;

е) MD и BC – скрещивающиеся, т.к. не принадлежат одной плоскости.

Задача 2.

Прямая с пересекает прямую а, параллельную прямой b. Докажите, что b и c – скрещивающиеся прямые.

Доказать: с и b – скрещиваются

Доказательство

1. .

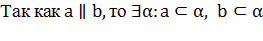
Т.к., по условию задачи, , то через них можно провести плоскость, т.е. существует некоторая плоскость α, содержащая прямые a и b

2.

Прямые a и c пересекаются. Обозначим точку пересечения буквой M. Так как прямые a и b параллельны, то M не принадлежит b.

3. Ч.т.д.

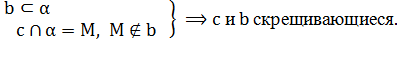
1. Дайте определение скрещивающихся прямых.

2. Дайте определение параллельных прямых.

3. Дайте определение пересекающихся прямых.

4. Какие существуют варианты взаимного расположения двух прямых в пространстве.

5. Сформулируйте теоремы о скрещивающихся прямых.

6. Дайте определение сонаправленных лучей.

7. Сформулируйте теорему о равенстве углов с сонаправленными сторонами.

8. В случае пересекающихся прямых чему равен угол ?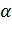

Литература

1. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 классы: учеб. для общеобразоват. организаций : базовый и углубл. уровни / [Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др.].- 3-е изд.- М.: Просвещение, 2016.- 255с.

1. Геометрия. 10-11 класс : учебник для учащихся общеобразовательных учреждений (базовый и профильный уровни) / И. М. Смирнова, В. А. Смирнов. – 5-е издание, исправленное и дополненное – М. : Мнемозина, 2008. – 288 с.

Источник