Что значит тупоугольный треугольник
Тупоугольный треугольник – площадь, определение, свойства
Тупоугольный треугольник мало чем отличается от обычных произвольных остроугольных треугольников, но тупой угол делает треугольник непривычным для восприятия. Это зачастую приводит в недоумение, поэтому стоит рассмотреть различные варианты решения задач на нахождение параметров тупоугольного треугольника.
Определения
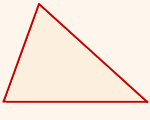
Тупоугольным треугольником будет называться любой треугольник, содержащий тупой угол. Тупоугольный треугольник может быть равнобедренным, но при этом не может быть равносторонним или прямоугольным. Собственно на этом свойства этой фигуры заканчиваются. В остальном это обычный треугольник и подход к решению таких фигур ничем не отличается.
Рис. 1. Тупоугольный треугольник.
В треугольнике сумма углов равна 180 градусам, поэтому только один угол треугольника может быть тупым, два других при этом всегда острые. Площадь тупоугольного треугольника находится так же, как площадь произвольного треугольника.
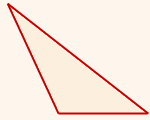
Рис. 2. Высота в тупоугольном треугольнике.
Только в тупоугольном треугольнике высота может лежать за пределами треугольника.
Рассмотрим несколько интересных задач на нахождение данных в тупоугольном треугольнике.
Пример решения задачи
Рис. 3. Рисунок к задаче.
Для решения любой задачи можно найти несколько способов. В данной ситуации можно пойти через площадь треугольников, достроить тупоугольный треугольник до прямоугольного или воспользоваться теоремой косинусов. Каждый из способов дает представление о том, как можно решать задачи с тупоугольным треугольником. Воспользуемся каждым из них.
Ответ в каждом случае должен быть одинаков. Но если округлять неточные ответы, то в одной задаче при одинаковых решениях можно получить разные величины. Будьте внимательны, результат не должен отличаться больше, чем на 1.
Теперь запишем две формулы площади, выразим через них высоту и найдем ее значение.
Тогда синус, как и в первом способе, выразим через основное тригонометрическое тождество.
$$sqrt<13+4+4>=sqrt<21>=sqrt<9*3>=3sqrt<3>$$ – по теореме косинусов.
Значение синуса угла АВС определим по основному тригонометрическому тождеству.
Выразим искомый синус угла АСВ.
Выразим из треугольника АМС и найденного значения синуса сторону АМ.
Ответы всех трех способов совпали, а значит задача решена верно.
Что мы узнали?
Математика. 3 класс
Конспект урока
Виды треугольников по видам углов. Закрепление изученного материала
Перечень вопросов, рассматриваемых в теме:
Какие виды треугольников различают по видам углов?
Как различать треугольники: прямоугольный, тупоугольный, остроугольный?
Геометрия – это раздел математики, изучающий геометрические фигуры и их свойства.
Треугольник – геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
Виды треугольников по величине углов
Остроугольный треугольник – это треугольник, в котором все три угла острые, т.е. меньше 90°.
Прямоугольный треугольник – это треугольник, в котором один угол прямой, т.е. 90º.
Тупоугольный треугольник – это треугольник, содержащий тупой угол, т.е. один из его углов лежит в пределах между 90° и 180°.
Основная и дополнительная литература:
1. Моро М. И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 85-87.
2. Волкова С. И. математика. Тесты. 3 кл. – М.: Просвещение, 2018. С. 60-67.
3. Рудницкая В. Н. Математика. Дидактические материалы. ч.1 3 кл. – М. «Вентана- Граф», 2016, с. 47-53.
Теоретический материал для самостоятельного изучения
Давайте вспомним, что вы уже знаете о видах треугольников.
По длине сторон различают: разносторонние, равнобедренные и равносторонние треугольники.
Но было бы несправедливо разделить все треугольники на 3 вида по длине сторон. Ведь у каждого есть ещё и по три угла.
У вас уже появились идеи?
Острые – меньше прямого
Прямые – угол 90 градусов
Тупые – больше прямого
Оказывается, по величине углов все треугольники тоже можно разделить на 3 вида:
те, у которых все углы острые, – остроугольные,
те, у которых есть прямой угол, – прямоугольные,
те, у которых есть тупой угол, – тупоугольные.
Для того чтобы безошибочно определить вид треугольника по величине углов, необходимо измерить все три угла при помощи транспортира.
Обычно вид треугольника можно определить на глаз.
Попробуйте определить виды треугольников по величине углов без измерений.
тупоугольный– 2, 4, 7, 5
По величине углов различают 3 вида треугольников:
Остроугольные, прямоугольные и тупоугольные
Определить вид треугольника можно тремя способами:
с помощью измерений, на глаз и по условным обозначениям.
Теперь вы можете различать виды треугольников по сторонам и по углам. Эти знания необходимы в геометрии.
Задания тренировочного модуля
Остроугольный треугольник – это треугольник, у которого ……………………
Прямоугольный треугольник – это треугольник, у которого есть ……………………
Тупоугольный треугольник – треугольник, все стороны которого есть ……………………
Правильные варианты ответов:
Остроугольный треугольник — это треугольник, у которого все углы острые.
Прямоугольный треугольник — это треугольник, у которого есть прямой угол.
Тупоугольный треугольник — треугольник, все стороны которого есть тупой угол.
Определите вид треугольника по величине углов и выпишите номера треугольников по порядку:
Тупоугольный треугольник, элементы, свойства, признаки и формулы
Тупоугольный треугольник, элементы, свойства, признаки и формулы.
Тупоугольный треугольник – это треугольник, у которого один угол тупой.
Тупоугольный треугольник (понятие и определение):
Тупоугольный треугольник – это треугольник, у которого один угол тупой, т.е. один из его углов лежит в пределах между 90° и 180°.
Рис. 1. Тупоугольный треугольник
∠ BАC– тупой угол треугольника,
Рис. 2. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника,
Рис. 3. Прямоугольный треугольник
Рис. 4. Равнобедренный треугольник
АВ = AС – боковые стороны, BС – основание,
Хотя в тупоугольном треугольнике тупой угол больше 90 градусов, сумма углов в треугольнике всегда равна 180 градусам.
Элементы тупоугольного треугольника:
Кроме сторон и углов у тупоугольного треугольника также имеются внешние углы. Внешний угол это угол, смежный с внутренним углом треугольника. У любого треугольника, в т.ч. тупоугольного, 6 внешних углов, по 2 на каждый внутренний. Внешний угол тупого угла тупоугольного треугольника всегда будет острым углом. Внешний угол острого угла тупоугольного треугольника всегда будет тупым углом.
Рис. 5. Тупоугольный треугольник и внешний угол
Медиана тупоугольного треугольника (как и любого другого треугольника), соединяющая вершину треугольника с противоположной стороной, делит ее пополам, т.е. на два одинаковых отрезка.
Рис. 6. Тупоугольный треугольник и медиана тупоугольного треугольника
MA – медиана тупоугольного треугольника
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Рис. 7. Тупоугольный треугольник и высота тупоугольного треугольника
MС – высота тупоугольного треугольника
Высота тупоугольного треугольника может лежать за пределами треугольника.
Биссектриса в тупоугольном треугольнике (как и в любом другом треугольнике) делит угол пополам. Биссектрисы пересекаются в точке, которая является центром вписанной окружности.
Рис. 8. Тупоугольный треугольник и биссектриса угла тупоугольного треугольника
MA – биссектриса тупого угла тупоугольного треугольника
Кроме того, биссектриса тупоугольного треугольника (как и любого другого треугольника) делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника
Свойства тупоугольного треугольника:
Свойства тупоугольного треугольника аналогичны свойствам обычного треугольника:
1. Против большей стороны лежит больший угол, и наоборот.
Рис. 9. Тупоугольный треугольник
2. Против равных сторон лежат равные углы, и наоборот.
Рис. 10. Тупоугольный треугольник с равными боковыми сторонами
3. Сумма углов тупоугольного треугольника равна 180°.
4. Любая сторона тупоугольного треугольника меньше суммы двух других сторон и больше их разности:
Виды треугольников
Треугольники бывают остроугольными, тупоугольными, прямоугольными, разносторонними, равносторонними, равнобедренными.
Определение 1. Треугольник называется остроугольным, если все ее углы острые, т.е. меньше 90° (Рис.1).
 |
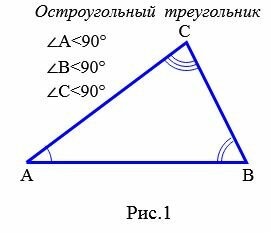Определение 2. Треугольник называется тупоугольным, если один из его углов тупой, т.е. больше 90° (Рис.2).
 |
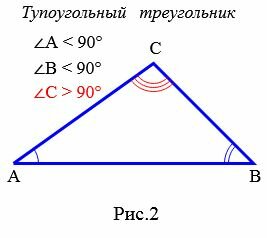Если треугольник тупоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.
Определение 3. Треугольник называется прямоугольным, если один из его углов прямой, т.е. равен 90° (Рис.3).
 |
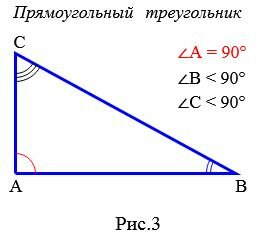Если треугольник прямоугольный, то исходя из того, что сумма всех углов треугольника равна 180°, остальные два угла треугольника будут острыми.
Определение 4. Треугольник называется разносторонним, если длины всех сторон треугольника разные (Рис.4).
 |
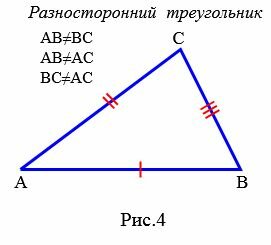Определение 5. Треугольник называется равносторонним или правильным, если длины всех сторон равны (Рис.5).
 |
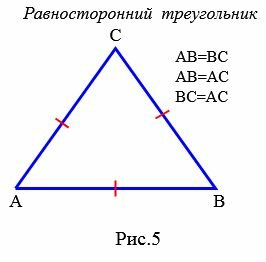Определение 6. Треугольник называется равнобедренным, если длины двух сторон равны (Рис.6).
 |
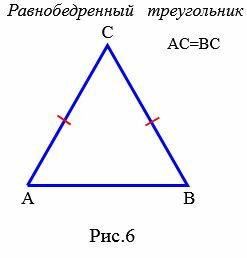В равнобедренном треугольнике равные стороны называются боковыми сторонами треугольника, а третья сторона называется основанием.
Виды треугольников
В зависимости от величин углов и соотношения длин сторон различают следующие виды треугольников.
Виды треугольников по углам:
Остроугольный треугольник — это треугольник, все углы которого острые (то есть градусная мера каждого угла меньше 90º).
Прямоугольный треугольник — это треугольник, у которого один угол прямой (то есть имеет градусную меру 90º).
Тупоугольный треугольник — это треугольник, у которого один угол — тупой (то есть имеет градусную меру больше 90º).
Виды треугольников по сторонам:
Равносторонний треугольник (или правильный треугольник) — это треугольник, у которого все три стороны равны.
Равнобедренный треугольник — это треугольник, у которого две стороны равны.
Разносторонний треугольник — треугольник, все стороны которого имеют разную длину.
Если в задаче ничего не сказано о виде треугольника, его считают произвольным, то есть разносторонним.
Отрезки равной длины на чертеже отмечают равным количеством черточек: