Что значит три черты в таблице истинности
Что значит три черты в таблице истинности
Значения логической функции для разных сочетаний значений входных переменных — или наборов входных переменных — обычно задаются специальной таблицей. Такая таблица называется таблицей истинности (комбинационной таблицей). Количество наборов входных переменных (Q) можно определить по формуле:Q=2n, где n — количество входных переменных.
Простейшим примером логической функции является функция одной переменной:
| Аргумент | Функция | |||
| X | F0(X) | F1(X) | F2(X) | F3(X) |
| 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 |
Тождественно-истинные функции – это логические функции, истинные на всех наборах значений входных переменных.
Тождественно ложные функции – это логические функции, ложные на всех наборах значений входных переменных.
Что значит три черты в таблице истинности
2) Логическое сложение или дизъюнкция:
Таблица истинности для дизъюнкции
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 1 |
| 0 | 1 | 1 |
| 0 | 0 | 0 |
3) Логическое отрицание или инверсия:
Таблица истинности для инверсии
| A | ¬ А |
| 1 | 0 |
| 0 | 1 |
4) Логическое следование или импликация:
«A → B» истинно, если из А может следовать B.
Обозначение: F = A → B.
Таблица истинности для импликации
| A | B | F |
| 1 | 1 | 1 |
| 1 | 0 | 0 |
| 0 | 1 | 1 |
| 0 | 0 | 1 |
5) Логическая равнозначность или эквивалентность:
Информатика
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
Способы решения задач по логике
Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:
Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.
Этапы решения логических задач:
Табличный способ – этапы, особенности
Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.
Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.
Метод таблиц
Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.
Существует общий алгоритм построения таблиц:
Если необходимо перебрать все значения простых выражений, то для задач:
Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.
Обязательно учитывают приоритет операций:
Обозначение логических операций:
Сравнение методов решения
Метод рассуждений
Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.
Пример №1.
Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.
Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:
Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:
Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.
Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.
Такой подход лучше не использовать, если условие сложное или много данных.
Табличный метод
Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).
Чтобы построить таблицу истинности логических выражений, следует:
Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:
Рассмотрим тот же пример.
Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:
Метод компактнее, для некоторых задач нагляднее.
Построение таблиц истинности для различных типов задач
Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.
Пример 2.
Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.
Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:
А — «Первый студент летал в Англию»;
В — «Второй студент летал в Англию»;
С — «Третий студент летал в Англию».
Запишем выясненные данные при помощи логических операций:
Пример 3.
Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:
По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.
Выясним, какие же классы добились высшего бала.
Разбиваем условие задачи на элементарные высказывания:
А – «А добьется высшего бала»;
В – «В добьется высшего бала»;
С – «С добьется высшего бала».
Запишем логические операции, описанные в примере:
Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.
Пример 4.
Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:
Предложенные имена: Арина, Артур, Кэтрин, София.
Решим задачу, используя таблицу.
Сначала решим пошагово, выполняя операции по приоритету:
Указанному условию соответствует первое имя.
Пример 5.
Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.
Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.
Маша Марина: «Саша заняла второе место, а Света – первое».
Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».
Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».
Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».
Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».
Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.
Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.
Построение электронных схем, реализующих логические операции
Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.
Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.
Электросхема с конъюнктором
Рассмотрим все варианты:
Заключение – эта электрическая цепь реализует операцию «И».
Дизъюнктор, схема электропитания
Рассмотрим этот вид электрической цепочки:
Заключение – такой вид электросхем соответствует логической операции «ИЛИ».
Инвертор в электросхемах
В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.
Заключение: схема соответствует логической операции «НЕ».
Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.
Обозначение логических элементов
Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.
Логические выражения и таблица истинности
Логические выражения и таблица истинности
Таблица истинности — таблица, показывающая, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний.
Логическое выражение — составные высказывания в виде формулы.
Равносильные логические выражения – логические выражения, у которых последние столбцы таблиц истинности совпадают. Для обозначения равносильности используется знак «=».
Алгоритм построения таблицы истинности:
1. подсчитать количество переменных n в логическом выражении;
3. подсчитать количество логических операций в формуле;
4. установить последовательность выполнения логических операций с учетом скобок и приоритетов;
5. определить количество столбцов: число переменных + число операций;
6. выписать наборы входных переменных;
7. провести заполнение таблицы истинности по столбцам, выполняя логические операции в соответствии с установленной в пункте 4 последовательностью.
Заполнение таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
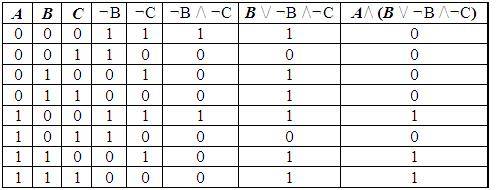
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
Количество логических переменных 3, следовательно, количество строк — 2 3 = 8.
Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов — 3 + 5 = 8.
1. В выражении две переменные А и В (n=2).
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
Таблица истинности логических выражений
Содержание:
Построение таблиц истинности для логических выражений
Для логического выражения можно построить таблицу истинности, показывающую, какие значения принимает выражение при всех наборах значений входящих в него переменных. Для построения таблицы истинности следует:
Построим таблицу истинности для логического выражения 
нём две переменные, две операции, причём сначала выполняется конъюнкция, а затем — дизъюнкция. Всего в таблице будет четыре столбца:
По этой ссылке вы найдёте полный курс лекций по высшей математике:
Заполненная таблица истинности имеет вид:
Обратите внимание, что последний столбец (результат) совпал со столбцом А. В таком случае говорят, что логическое выражение 
равносильно логической переменной А.
Возможно вам будут полезны данные страницы:
Свойства логических операций
Рассмотрим основные свойства логических операций, называемые также законами алгебры логики.
1. Переместительный (коммутативный) закон:
• для логического умножения:
• для логического сложения:
2. Сочетательный (ассоциативный) закон:
• для логического умножения:
• для логического сложения:
При одинаковых знаках операций скобки можно ставить произвольно или вообще опускать.
3. Распределительный (дистрибутивный) закон:
• для логического умножения:
• для логического сложения:
4. Закон двойного отрицания:
Двойное отрицание исключает отрицание.
5. Закон исключённого третьего:
• для логического умножения:
• для логического сложения:
Из двух противоречивых высказываний об одном и том же предмете одно всегда истинно, а второе — ложно, третьего не дано.
6. Закон повторения:
• для логического умножения:
• для логического сложения:
7. Законы операций с 0 и 1:
• для логического умножения:
• для логического сложения:
8. Законы общей инверсии:
• для логического умножения:
• для логического сложения:
Законы алгебры логики могут быть доказаны с помощью таблиц истинности
Докажем распределительный закон для логического сложения:
Совпадение значений в столбцах, соответствующих логическим выражениям в левой и правой частях равенства, доказывает справедливость распределительного закона для логического сложения.
Примеры с решением
Пример 1.
Найдём значение логического выражения 
для числа X = 0.
Решение:
При X = 0 получаем следующее логическое выражение: 
. Так как логические выражения 0
Для решения задач вам понадобится знание таблиц истинности логических операций:
А также, вы должны знать:
Порядок выполнения логических операций задается круглыми скобками
Сначала выполняется операция отрицания НЕ
после И выполняется ИЛИ
и в последнюю очередь — эквивалентность.
Задача 1
Дан фрагмент таблицы истинности выражения F:
Какое выражение соответствует F?
Решение:
Чтобы определить верное выражение, надо значения А,В,С каждой из строк таблицы подставить в очередное выражение, определить его результат выполнения и сравнить со значением F соответствующей строки.
То выражение, значения которого совпадут со значениями столбца F, и будет искомым. Решение:
Задача 2
Дан фрагмент таблицы истинности выражения F:
Каким выражением может быть F?
Решение:
1) В каждом из приведенных выражений логические переменные связывает только один тип логической операции. В 1 и 3 вариантах это операция И (
), во 2 и 4 вариантах это операция ИЛИ (
).
2) По столбцу F видно, что выражение для двух комбинаций данных истинно, а для одной — ложно. Следовательно, выражение не может быть логическим умножением (И), так как логическое умножение истинно только для одной комбинации данных, а в таблице две истины. Следовательно, искомое выражение является логическим сложением (ИЛИ) значений логических переменных.
Поэтому, в качестве ответа может быть 2 или 4 вариант. Рассмотрим их.
1) 2-й вариант: В первой строке таблицы истинности отображены только значения х1, хЗ, х5, и все они равны 0. Но в формуле 2го варианта у нас х5 отрицается, то есть значение х5 будет изменено на 1, и в результате всё выражение должно быть истинным. Что не соответствует заданной таблице. Остаётся 4-й вариант.
2) Как мы видим, переменные х1, хЗ и х5 в 4-м варианте ответа не отрицаются, что соответствует первой строке заданной таблицы.
Задача 4
Какое из приведенных имен сказочных героев удовлетворяет логическому условию:
Решение:
Составим для каждого из предложенных ответов схему соответственно заданной логической формуле. Ищем истинное значение.
И так с каждым вариантом ответа, пока не найдете истину.
Задача 5
Логическая функция F задаётся выражением 
Определите, какому столбцу таблицы истинности функции F соответствует каждая из
переменных X, Y, Z
Решение 1:
Последней операцией выполнения является операция 
. Поэтому выражение 
имеет значение ИСТИНА, когда 
Рассмотрим все случаи, когда F = 1 (это значения в строках 1 и 3):
— не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.
— не рассматриваем, т.к. в табл, нет строки, где все значения логических переменных = 1.
Рассматриваем только 1 и 3 строки таблицы:
Решение 2:
Последней операцией выполнения является операция 
. Поэтому выражение
имеет значение ИСТИНА, когда 
Выражение F равно 1 в 1й и Зй строках, в этих же строках только “Перем.3”=1, следовательно, значение X находится в 3-м столбце.
Теперь рассмотрим построчно значения 1-х двух столбцов:
1 строка: 0 и О, Y = Z. Поэтому Y и Z для столбцов не определить.
2 строка: 0 и 1. Независимо будет ли Y=0 Z=1 или Y=1 Z=0, функция F=0 т.к. уже
Х=0. Поэтому Y и Z для столбцов не определить.
3 строка: 0 и 1. В этой строке функция F=1, значит 
Комбинация 
невозможна, иначе F будет = 0. Комбинация 
то, что надо. Следовательно, значение Y находится в 1-м столбце а значение Z во 2-м.
Присылайте задания в любое время дня и ночи в ➔ 
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.