Что значит сумма цифр числа

Математика для блондинок

Страницы

воскресенье, 18 марта 2018 г.

Сумма цифр числа

Давайте разберемся, что и как мы делаем для того, чтобы найти сумму цифр заданного числа. И так, пусть у нас есть число 12345. Что нужно сделать для того, чтобы найти сумму цифр этого числа? Рассмотрим все шаги по порядку.

1. Записываем число на бумажке. Что же мы сделали? Мы преобразовали число в графический символ числа. Это не математическое действие.

Разрезание графического символа

3. Преобразовываем отдельные графические символы в числа. Это не математическое действие.

Преобразование цифр в числа

4. Складываем полученные числа. Вот это уже математика.

Сложение чисел

Сумма цифр числа 12345 равна 15. Вот такие вот «курсы кройки и шитья» от шаманов применяют математики. Но это ещё не всё.

С точки зрения математики не имеет значения, в какой системе счисления мы записываем число. Так вот, в разных системах счисления сумма цифр одного и того же числа будет разной. В математике система счисления указывается в виде нижнего индекса справа от числа. С большим числом 12345 я не хочу голову морочить, рассмотрим число 26 из статьи про странный значок. Запишем это число в двоичной, восьмеричной, десятичной и шестнадцатеричной системах счисления. Мы не будем рассматривать каждый шаг под микроскопом, это мы уже сделали. Посмотрим на результат.

Сумма цифр числа

Как видите, в разных системах счисления сумма цифр одного и того же числа получается разной. Подобный результат к математике никакого отношения не имеет. Это всё равно, что при определении площади прямоугольника в метрах и сантиметрах вы получали бы совершенно разные результаты.

Полученный результат следует рассматривать как доказательство того, что системы счисления являются единицами измерения чисел. Ведь мы не можем сравнивать числа с разными единицами измерения. Если одни и те же действия с разными единицами измерения одной и той же величины приводят к разным результатам после их сравнения, значит это не имеет ничего общего с математикой.

Что же такое настоящая математика? Это когда результат математического действия не зависит от величины числа, применяемой единицы измерения и от того, кто это действие выполняет.

Источник

О сумме цифр, обобщённом признаке делимости и одной нерешённой задаче

Почему признаки делимости именно такие?

Все знают, что если сумма цифр числа делится на 9, то и сумма его цифр делится на 9. А для определения, делится ли число на 11, нужно сложить его цифры, стоящие на чётных местах и отнять сумму цифр, стоящих на нечётных местах. Если результат будет делиться на 11, то и само число также будет делиться на 11.

Возникает вопрос: почему существуют признаки делимости? Иными словами, почему для ответа на вопрос, делится ли число m на число n, достаточно не выполнять деление, а провести некоторые операции с цифрами числа m? И как вывести признак делимости на произвольное n. К ответу на этот вопрос мы придём, решая одну, казалось бы, пустяковую задачку.

Возьмём какое-нибудь натуральное число, скажем, 17. Сумма его цифр равна 8. Если 17 умножить на 2, получим 34 и сумма цифр этого числа окажется равной 7. А у произведения 17*3=51 сумма цифр равна 6. Вопрос: на какое натуральное число нужно умножить 17, чтобы сумма цифр произведения была наименьшей?

Понятно, что сумма цифр, равная 1 будет только у степеней десятки, которые кратны лишь произведениям степеней двойки и пятёрки. Поэтому попробуем найти кратное 17-ти число вида 100…01 с суммой цифр, равной двум.

Чтобы последней цифрой произведения была единица, последней цифрой неизвестного множителя должна быть тройка. Далее, т.к. 17*3=51, а предпоследняя цифра произведения равна 0, то предпоследней цифрой неизвестного множителя должна быть пятёрка.
17*53=901

Далее находим, последовательно:
17*2353=40001
17*82353=1400001
17*882353=15000001
17*5882353=100000001 (!)

Весь этот процесс представлен на анимированной гиф-иллюстрации

Итак, среди чисел, кратных 17-ти наименьшая сумма цифр, равная 2, будет у числа 100000001=17*5882353.

Ответ: число 17 нужно умножить на 5882353, и тогда сумма цифр произведения будет равна 2.

Возникает вторая задача: а что было бы, если бы потребовалось найти кратное с минимальной суммой цифр для какого-нибудь другого числа? Почти сразу приходят на ум числа 3 и 9, кратные которых, вследствие соответствующих признаков делимости, не могут иметь суммы цифр, меньшие, чем 3 или 9, соответственно. Но оказывается, что и многие другие числа не имеют кратных вида 100…01.

К примеру, попробуем провести операции, аналогичные проведённым с числом 17, для числа 41.

Если существует такой множитель Х, что 41*Х=100…01, то последняя цифра числа Х равна 1.
41*1=41.
Далее, предпоследняя цифра числа Х должна быть равна 6
41*61=2501
Далее получаем, последовательно:
41*561=23001
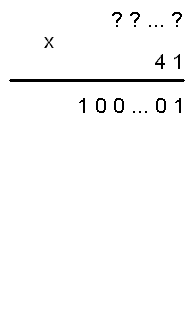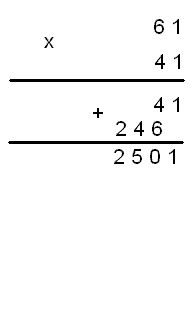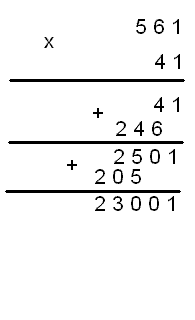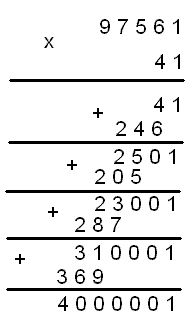
41*7561=310001
41*97561=4000001

И тут мы обнаруживаем, что зациклились: далее неизвестный множитель будет продолжать обрастать цифрами 6, 5, 7 и 9, а сумма цифр кратного, равная 2, достигнута не будет.

Итак, какова же минимальная сумма цифр у числа, кратного 41-му?

Вот тут мы и приходим к проблеме построения обобщённого признака делимости. Почему же для ответа на вопрос, делится ли число m на число n, достаточно не выполнять деление, а провести некоторые операции с цифрами числа m?

Как известно, если число m имеет k цифр, то его можно представить в виде суммы произведений его цифр на соответствующие степени десятки: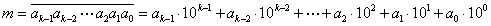

Далее, известно, что сумма остатков равна остатку суммы, а произведение остатков равно остатку произведения. Тогда, если j-я степень десятки даёт остаток 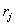при делении на n, то остаток числа m при делении на n будет равен остатку от деления на n выражения

Этот обобщённый признак делимости называется признаком Паскаля.

Докажем теперь с помощью этого признака делимости, что не существует числа вида 100…01, которое делится на 41. Вычислим остатки от деления на 41 степеней десятки:

Источник

Как легко понять знаки Σ и П с помощью программирования

Для тех, кто подзабыл матешу

Вот говорят, что если ты не закончил Физтех, ФПМ или Бауманку, тебе в программировании делать нечего. Почему так говорят? Потому что, дескать, ты не учил сложную математику, а в программировании без неё никуда.

Это всё чушь, конечно. Если вы плохо знаете математику, вы можете быть блестящим разработчиком. Вы вряд ли напишете драйверы для видеокарты, но вы запросто сделаете мобильное приложение или веб-сервис. А это — основные деньги в этой среде.

Но всё же, чтобы получить некоторое интеллектуальное превосходство, вот вам пара примеров из страшного мира математики. Пусть они покажут вам, что не все закорючки в математике — это ад и ужас. Вот две нестрашные закорючки.

Знак Σ — сумма

Когда математикам нужно сложить несколько чисел подряд, они иногда пишут так:

Σ (читается «сигма») — это знак алгебраической суммы, который означает, что нам нужно сложить все числа от нижнего до верхнего, а перед этим сделать с ними то, что написано после знака Σ.

На картинке выше написано следующее: «посчитать сумму всех чисел от 5 до 15, умноженных на два». То есть:

Давайте для закрепления ещё один пример. На картинке ниже будет сказано «Найди сумму квадратов чисел от 5 до 10». То есть «возьми все числа от 5 до 10, каждое из них возведи в квадрат, а результаты сложи».

Но мы с вами как программисты видим, что здесь есть повторяющиеся действия: мы много раз складываем числа, которые меняются по одному и тому же правилу. А раз мы знаем это правило и знаем, сколько раз надо его применить, то это легко превратить в цикл. Для наглядности мы показали, какие параметры в Σ за что отвечают в цикле:

Произведение П

С произведением в математике работает точно такое же правило, только мы не складываем все элементы, а перемножаем их друг на друга:

А если это перевести в цикл, то алгоритм получится почти такой же, что и в сложении:

Что дальше

Сумма и произведение — простые математические операции, пусть они и обозначаются страшными символами. Впереди нас ждут интегралы, дифференциалы, приращения и бесконечные ряды. С ними тоже всё не так сложно, как кажется на первый взгляд.

Источник

Нумерология: никакого гадания, только теория чисел

В данной статье речь пойдёт о таких понятиях теории чисел, как цифровой корень и ведический квадрат.

Данная статья ничего не говорит о нумерологии, кроме того, что это псевдонаучная концепция.

Цель данной статьи: показать математические закономерности вокруг вычисления цифрового корня и его связь с циклическими числами.

Введение

Несколько дней назад я решил написать незатейливую статью про нумерологическое сложение. Моей целью было показать, что даже такая незамысловатая операция может иметь большое количество интересных закономерностей. Многие из этих закономерностей я нашёл ещё в школьное время, когда скучал на уроках географии. При внимательном рассмотрении я нашёл больше закономерностей, чем ожидал, и это привело меня назад к моей любимой теме full reptend prime.

После я внимательно изучил то, что нашёл, узнал, что многие из этих понятий уже существуют, и решил переписать статью заново, чтобы опираться на общеизвестные понятия. Помимо известных понятий я добавил собственные визуализации, чтобы сделать чтение немного более увлекательным.

Сумма цифр и цифровой корень

Аддитивная стойкость натурального числа — это количество итераций, на которых нужно применить операцию суммы цифр, для того чтобы получить цифровой корень.

Пример: Цифровая сумма числа 142857 равна 1 + 4 + 2 + 8 + 5 + 7 = 27

Цифровая сумма числа 27 равна 2 + 7 = 9

Как следствие, цифровой корень числа 142857 = 9, аддитивная стойкость 142857 = 2.

Код для вычисления цифрового корня в произвольной системе счисления на языке Python:

Применение цифровой суммы

Цифровые суммы применялись при расчёте контрольных сумм для проверки арифметических операций ранних компьютеров. Ранее, в эпоху ручного счета, Фрэнсис Исидор Эджуорт предложил использовать суммы 50 цифр, взятых из математических таблиц логарифмов, в качестве формы генерации случайных чисел; если предположить, что каждая цифра случайна, то по центральной предельной теореме эти цифровые суммы будут иметь случайное распределение, близкое к гауссову распределению.

Цифровая сумма двоичного представления числа известна как вес Хэмминга или численность населения. Алгоритмы выполнения этой операции были изучены, и она была включена в качестве встроенной операции в некоторые компьютерные архитектуры и некоторые языки программирования. Эти операции используются в вычислительных приложениях, включая криптографию, теорию кодирования и компьютерные шахматы.

Улучшение алгоритма вычисления цифрового корня

Свойства цифрового корня

Операция сложения

Сделаем небольшую таблицу, для того чтобы изучить закономерности, каким образом вычисляется цифровой корень суммы двух чисел:

Таблица для анализа операции цифрового корня суммы двух чисел.

Код для построения таблицы суммы:

Как можно увидеть, цифровой корень суммы чисел равен цифровому корню суммы цифровых корней этих чисел:

Операция вычитания

Формула похожа на предыдущую, однако совпадает не полностью.

Операция умножения

Выведем вариацию таблицы умножения, для того чтобы исследовать эту операцию:

Расчет цифрового корня от двух множителей

Код для вывода таблицы умножения:

Запишем значения для каждого множителя:

1) [1, 2, 3, 4, 5, 6, 7, 8, 9]

2) [2, 4, 6, 8, 1, 3, 5, 7, 9]

3) [3, 6, 9, 3, 6, 9, 3, 6, 9]

4) [4, 8, 3, 7, 2, 6, 1, 5, 9]

5) [5, 1, 6, 2, 7, 3, 8, 4, 9]

6) [6, 3, 9, 6, 3, 9, 6, 3, 9]

7) [7, 5, 3, 1, 8, 6, 4, 2, 9]

8) [8, 7, 6, 5, 4, 3, 2, 1, 9]

9) [9, 9, 9, 9, 9, 9, 9, 9, 9]

Последовательности для множителей 1, 2, 3, 4. Они же являются зеркальными для 8, 7, 6, 5.

Для нахождения последовательности любой линии можно записать формулу:

Если записать эти значения как множество пересечений всех множителей, мы получим в результате ведический квадрат.

Ведический квадрат для десятичной системы счисления.

Приведение ведического квадрата к латинскому квадрату в десятичной системе счисления.

В результате мы получим:

Подмножество ведического квадрата, составляющее латинский квадрат в десятичной системе счисления.

Если переставить некоторые из его строчек местами, мы получим последовательность циклических чисел. О том, каким образом должны быть осуществлены перестановки строчек, будет рассказано ниже при исследовании других операций с цифровым корнем.

Ведические квадраты для систем счисления 100 и 1000.

Теперь вернемся к произведению. Цифровой корень произведения одиночных цифр в заданной системе счисления вычисляется при помощи соответствующего ведического квадрата.

Для вычисления цифрового корня произведения двух чисел, которые содержат больше одной цифры, для начала нужно вычислить цифровой корень каждой из этих цифр, и после этого воспользоваться ведической площадью.

Операция деления

Рассмотрим те числа, которые дают при делении непериодические дроби, это 2, 5, 4, 8.

Для того чтобы быть уверенными, что мы не допускаем ошибок, воспользуемся уже выведенными правилами и умножим результат деления на 1000; так как цифровой корень 1000 равен 1, то произведение будет иметь тот же самый цифровой корень.

Таблица деления для делителей, которые взаимно просты с десятичной системой счисления.

Тут бросаются в глаза несколько закономерностей. Число 9 не только при умножении, но и при делении приводит к значению цифрового корня, равному 9. Интересное происходит также с числами 3 и 6, эти числа как при умножении, так и при делении дают абсолютно одинаковые значения цифрового корня.

Запишем в таблицу череду делений:

Операция деления для цифрового корня определена только для делителей, которые не являются взаимно простыми с основанием системы счисления.

Операция возведения в степень

Таблица возведения в степень:

Таблица возведения в степень в десятичной системе счисления.

Здесь мы можем наблюдать цикличность.

Рассмотрим систему счисления 8, череда его значений будет равна [1, 3, 2, 6, 4, 5]. Именно такие же остатки от деления мы получаем при делении числа в десятичной системе счисления.

Деление 1 на 7 в столбик. Здесь мы можем наблюдать остатки от деления [1, 3, 2, 6, 4, 5]. Последовательность полученная при возведении в степень, в восьмеричной системе счисления.

Это свойство связано с тем, что вычисление цифрового корня можно осуществить при помощи альтернативной формулы расчета цифрового корня:

Ещё визуализации

Остатки от деления, найденные в 6 системе счисления, связанные с числом 5. Остатки от деления, найденные в 10 системе счисления, связанные с квадратом числа 3. Остатки от деления, найденные в 12 системе счисления, связанные с числом 11. Остатки от деления, найденные в 14 системе счисления, связанные с числом 13. Остатки от деления, найденные в 18 системе счисления, связанные с числом 17. Остатки от деления, найденные в 20 системе счисления, связанные с числом 19. Остатки от деления, найденные в 26 системе счисления, связанные с квадратом числа 5. Остатки от деления, найденные в 28 системе счисления, связанные с кубом числа 3.

Теперь приведём несколько картинок из ведических квадратов, принцип их формирования очень прост, потому ограничимся небольшим количеством:

Замкнутая фигура из 6 системы счисления, связана с числом 5. Замкнутые фигуры из 8 системы счисления, связанные с числом 7. Замкнутые фигуры из 12 системы счисления, связанные с числом 11.

Образование циклических чисел при помощи ведической площади и остатков от деления

После того как мы получили латинский квадрат из ведического квадрата, пронумеруем его строки последовательно:

Пронумерованный латинский квадрат.

Теперь мы можем переставить строки на основании череды остатков от деления, таким образом мы получим последовательность циклических чисел. Напомню, остатки от деления были равны [1, 3, 2, 6, 4, 5]. В результате у нас получится следующая картина:

Перестановки в пронумерованном латинском квадрате, в результате мы получили циклическое число.

Как можно наблюдать, первый столбец теперь представляет собой циклическое число 142857.

Выводы

Несмотря на плохую репутацию нумерологии, операции суммы цифр и цифрового корня имеют пусть не широкое, но всё же практическое применение.

Например, с помощью цифрового корня можно сформировать множество замкнутых n-вершинных звезд, многие из которых очень любят современные рок\метал группы 🙂

Как можно видеть, многие метал группы тоже любят теорию чисел!

Но лично я для своей метал группы решил выбрать анимированный логотип, составленный из одновременной визуализации периодических дробей, образованных из 90 рациональных дробей 1/91..90/91:

Почему я выбрал число 91, которое является произведением 7 и 13? Речь об этом пойдет в следующей статье 🙂

Если у кого-то есть дополнительная информация об описанных выше понятиях, пожалуйста присылайте её в комментарии, я буду очень благодарен!

Надеюсь, что вам было интересно, большое спасибо за внимание!

Источник

Сумма и произведение цифр числа

Найти сумму и произведение цифр, введенного натурального числа. Например, если введено число 325, то сумма его цифр равна 10 (3+2+5), а произведение 30 (3*2*5).

Pascal

Сумма цифр числа паскаль

Язык Си

Python

Сумма цифр числа python (питон)

КуМир

Basic-256

Сумма цифр числа паскаль

var
n, sum: word;
mult: longint;
begin
readln(n);
sum := 0;
mult := 1;
while n > 0 do begin
sum := sum + n mod 10;
mult := mult * (n mod 10);
n := n div 10;
end;
writeln(‘Sum: ‘, sum);
writeln(‘Mult: ‘, mult);
end.

main() <
int n, s, m;
scanf(«%d»,&n);
s = 0;
m = 1;
while (n>0) <
s += n%10;
m *= n%10;
n = n/10;
>
printf(«Сумма: %d\nПроизведение: %d\n», s, m);
>

245
Сумма: 11
Произведение: 40

Сумма цифр числа python (питон)

n = int(input())
s = 0
m = 1
while n>0:
s += n%10
m *= n%10
n = n//10
print(«Сумма:», s)
print(«Произведение:», m)

567
Сумма: 18
Произведение: 210

алг сумма цифр
нач
цел n, s, m
ввод n
s := 0
m := 1
нц пока n>0
s := s + mod(n,10)
m := m * mod(n,10)
n := div(n,10)
кц
вывод s, нс, m
кон

input n
sum = 0
mult = 1
while n > 0
sum = sum + n%10
mult = mult * (n%10)
n = n\10
endwhile
print «Сумма: » + sum
print «Произведение: » + mult

567
Сумма: 18
Произведение: 210

Источник