Что значит сумма квадратов
Сумма квадратов
Сумма квадратов встречается в ходе преобразования числовых и буквенных выражений. Как с ней работать?
Поскольку сумма квадратов является составной частью формул полного квадрата суммы и разности, можно попробовать применить одну из этих формул.
Формула полного квадрата суммы состоит из трёх слагаемых — сумма квадратов двух слагаемых плюс удвоенное произведение этих слагаемых. Следовательно, для получения полного квадрата к сумме квадратов двух выражений следует прибавить удвоенное произведение этих выражений, и, чтобы выражение не изменилось, вычесть это произведение:
Аналогично, для получения полного квадрата разности следует из суммы квадратов двух выражений вычесть удвоенное произведение этих выражений и тут же прибавить его:
Рассмотрим, как эти рассуждения могут быть применены на практике.
Теперь используем данные условия:
Эти рассуждения применяются, например, в приложении теоремы Виета, когда не решая квадратного уравнения, требуется найти сумму квадратов его корней и т.п.
Сумма квадратов всех целых чисел
Сумма квадратов чисел — математическое выражение, для которого не существует формулы сокращенного умножения. На практике иногда требуется быстро прикинуть сумму нескольких квадратов, однако без математических хитростей такое выражение подсчитать достаточно трудно.
Формулы сокращенного умножения
Для упрощения расчетов в математике используются специальные формулы сокращенного умножения, которые, по сути, представляют собой частные случаи бинома Ньютона. При помощи таких формул легко вручную подсчитать, например, квадрат суммы или разности вида:
(a ± b) 2 = a 2 ± 2ab + b 2
в учебниках по математике вы не найдете. Естественно, она есть для комплексных чисел, тех самых, с которыми мы знакомимся в университетском курсе математического анализа. Выглядит эта формула достаточно жутко:
где i – легендарная мнимая единица, которая рассчитывается как квадратный корень из минус единицы.
В школьных примерах продвинутые ребята негласно используют формулу, которая не входит в пантеон формул сокращенного умножения:
a 2 + b 2 = (a + b) 2 − 2ab.
Эта формула идеально подходит только для вычисления суммы квадратов двух целых чисел. Но что делать, если на практике требуется сложить сумму нескольких квадратов или рациональных чисел? Здесь на сцене появляется наша программа.
Наша программа позволяет сложить сколько угодно квадратов целых и рациональных чисел. Для вычислений вам потребуется ввести числа в ячейку, отделив их пробелом. Десятичные дроби записываются и с точкой, и с запятой. Рациональные числа записываются через / (слэш). Итак, вы можете подсчитать сумму нескольких квадратных чисел, но для чего это вообще нужно?
Рассмотрим примеры работы калькулятора
Разложение на квадраты
Зачем складывать квадраты целых чисел? Почему бы не складывать их кубы или 33-е степени? Эти вопросы встают перед каждым математиком, занимающимся теорией чисел. Разложение целых чисел на сумму двух квадратов — классическая задача теории чисел, за которой стоит исследование делимости. В целом задача эта обратна теме данной статьи: вопрос ставится таким образом, что математик должен вычислить, раскладывается ли данное число на сумму двух квадратов. Некоторые ученые идут дальше и пытаются раскладывать числа на суммы квадратов последовательных чисел. Мы же просто попробуем сложить некоторые квадраты и посмотрим, что получится в результате. Итак, введем в калькулятор следующие пары чисел:
Как видите, разные пары чисел дают один и тот же результат. Кроме того, сами числа 25 и 64 являются квадратами 5 и 8 соответственно. Магия теории чисел, которую трудно применить в каких-нибудь бытовых расчетах.
Гипотенуза 5-мерного тетраэдра
Представим еще менее реальную задачу. Пятимерный тетраэдр или 5-мерный симплекс — это обобщение треугольника для пятимерного пространства. Такие причудливые идеи используются в квантовой физике, теории относительности и барицентрическом исчислении, но для решения некоторых задач от вас не потребуется глубоких знаний высшей математики. К примеру, гипотенуза пятимерного тетраэдра рассчитывается по достаточно простой формуле:
где a, b, c, d – стороны симплекса.
Для решения такой задачки достаточно ввести четыре значения в форму онлайн калькулятора и вычислить квадратный корень из результата. Допустим, стороны симплекса в условных единицах имеют следующие значения: 1, 2.3, 3/5, 0,85. Введем этим данные в ячейку через пробел и получим 7,3725. Теперь вычислим квадратный корень и выясним, что гипотенуза пятимерного симплекса равна 2,715.
Заключение
Сумма квадратов нескольких чисел — нестандартная задача, которая вряд ли встретится в обычных бытовых расчетах, как-то вычисление диаметра дачного ограждения или площади пиццы. Для нетривиальных математических расчетов вам пригодится наша программа, которая быстро вычислит сумму квадратов сколько угодно большого количества целых и рациональных чисел.
Что значит сумма квадратов
Введение
ЗАЧЕМ СКЛАДЫВАТЬ КВАДРАТЫ ЦЕЛЫХ ЧИСЕЛ? Почему бы не складывать их кубы или 666-е степени? Вопросы эти весьма серьезны и встают перед каждым, кто начинает изучать математику. Из огромного разнообразия задач не все достойны пристального внимания. Задача о сумме квадратов — в высшей степени достойна. К сожалению для философа, это невозможно объяснить, не рассказав ее решение и не углубившись тем самым в детали.
«Детали» — это критерий того, какие натуральные числа представимы в виде суммы квадратов двух целых чисел. В доказательстве этого критерия будут использованы не только «обычные» целые числа, но и числа комплексные — прекрасный пример применения абстрактной теории к конкретной арифметической задаче! Хотя эта статья содержит лишь малую часть богатейшей теории делимости алгебраических чисел, надеемся, ее очарование никого не оставит равнодушным.
Суммы квадратов
Таблица сумм квадратов
Упражнение 1. Найдите наименьшее число, которое двумя существенно разными (т. е. не получающимися один из другого перестановкой слагаемых) способами представимо в виде суммы двух квадратов а) целых; 6) натуральных чисел.
Остатки от деления на 3
Наименьшее натуральное число, не представимое в виде суммы двух квадратов целых чисел, — это 3. Кратные 3 числа 6, 12, 15, 21 тоже не представимы, а вот числа 9 = 3 2 + 0 2 и 18 =3 2 + 3 2 — представимы. Возникает гипотеза: числа, которые кратны 3, но не кратны 9, не представимы в виде суммы двух квадратов. Эта гипотеза верна. Верно даже более сильное утверждение:
Теорема 1. Если сумма квадратов х 2 + у 2 целых чисел х, у кратна 3, то числа х, у тоже кратны 3.
Доказательство. Выпишем остатки от деления квадратов целых чисел на 3:
| Квадрат | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 |
| Остаток | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 1 |
Закономерность очевидна: остатки периодически повторяются, и никаких остатков кроме 0 и 1 не бывает.
(Точнее говоря, остаток от деления квадрата целого числа х на 3 равен 0, если х кратно 3, т. е. представимо в виде х = 3k, где k — целое число, и остаток равен 1, если x не кратно 3, т. е. представимо в виде х= 

Суммы остатков 0 + 1 и 1 + 1 не кратны 3. Значит, сумма квадратов х 2 + у 2 кратна 3 в том и только том случае, когда х и у кратны 3.
Остатки от деления на 7
Для доказательства составим таблицу остатков от деления квадратов на 7:
| Квадрат | 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 |
| Остаток | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 | 1 | 4 | 2 | 2 | 4 | 1 | 0 |
Остатки, как видите, периодически повторяются. Поскольку сумма никаких двух из остатков 1, 2, 4 не кратна 7, мы доказали нашу гипотезу.
Упражнения
3. Остаток от деления квадрата целого числа х на 7 равен 0, если х = 7k, где k — целое число; равен 1, если 


4. Докажите, что если сумма квадратов двух целых чисел кратна 21, то она кратна и 441.
5. а) Какие остатки дают квадраты целых чисел при делении на 11? б) Докажите, что если сумма квадратов двух целых чисел кратна 11, то она кратна 121. в) Докажите, что если сумма квадратов двух целых чисел кратна 1331, то она кратна и 14641.
Остатки от деления на 19
Например, пусть р = 19. Составим таблицу остатков от деления квадратов на 19:
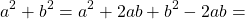
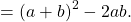
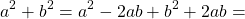
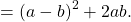
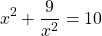



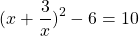
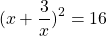
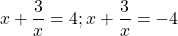

 существует такое целое число m, что m 2 + 1 кратно р.
существует такое целое число m, что m 2 + 1 кратно р.