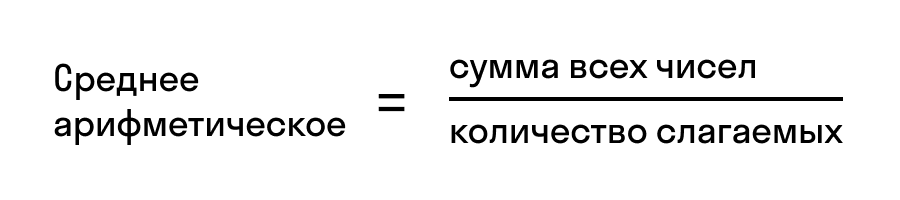Что значит среднее арифметическое
Простая формула, чтобы подсчитать среднее арифметическое
Понятие среднего арифметического
Среднее арифметическое нескольких чисел — это сумма этих чисел, которую разделили на количество слагаемых. Формула среднего арифметического, которую обычно проходят в 5 классе, выглядит так:
Потренируемся использовать формулу среднего арифметического.
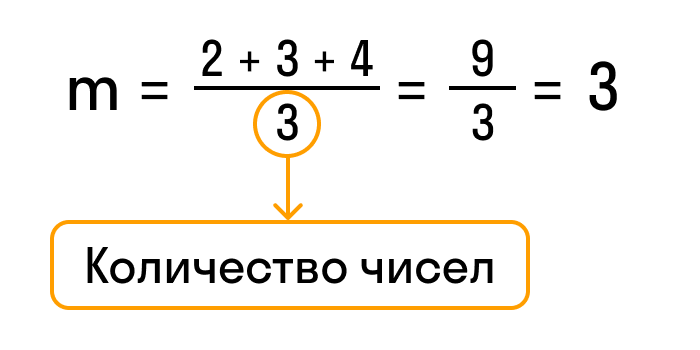
Например, найдем среднее арифметическое чисел 2, 3 и 4. Обозначим среднее значение латинской буквой «m» и посчитаем сумму этих чисел.
Разделим результат на количество чисел в задании, то есть на 3, и получим ответ — 3.
Применить эти знания можно в любой сфере жизни, где нужно обобщить и дать среднюю оценку: узнать среднюю цену товара в разных магазинах, вычислить среднюю зарплату сотрудников компании, сравнить среднюю посещаемость занятий учениками 5А и 5Б.
Средняя скорость движения — это весь пройденный путь, поделенный на время движения. Формула:
Так мы рассмотрели самые основные методы нахождения среднего значения. Теперь осталось попрактиковаться на примерах, чтобы быстро решать задачки на контрольной.
Примеры расчета среднего арифметического
Пример 1. Вычислить среднее арифметическое 33,3 и 55,5.
Чтобы найти среднее арифметическое двух чисел, надо сложить эти числа и результат разделить на 2: (33,3 + 55,5) : 2 = 88,8 : 2 = 44,4.
Пример 2. Подсчитать среднее арифметическое 7,5 и 8 и 0,5.
Чтобы найти среднее арифметическое трех чисел, надо сложить эти числа и результат разделить на 3: (7,5 + 8 + 0,5) : 3 = 16 : 3 = 5,33.
Пример 3. Найти среднее арифметическое 202, 105, 67 и 9.
Чтобы найти среднее арифметическое четырех чисел, надо сложить эти числа и результат разделить на 4: (202 + 105 + 67 + 9) : 4 = 383 : 4 = 95,75.
Пример 4. Сколько в среднем тратит школьник денег в неделю, если в понедельник он потратил 80 рублей, во вторник 75 рублей, в среду и четверг по 100 рублей, в пятницу 50 рублей.
Чтобы найти сколько в среднем школьник потратил за пять дней, надо сложить эти суммы и результат разделить на 5: (80 + 75 + 100 + 100 + 50) : 5 = 405 : 5 = 81.
Ответ: школьник в неделю тратит в среднем 81 рубль.
Еще больше интересных практических заданий — на курсах математики в онлайн-школе Skysmart. Вводный урок — бесплатно!
Среднее арифметическое: физический смысл и визуализация
Переменная величина – атрибут (свойство) системы, меняющий свое числовое значение. Множество значений переменой величины может иметь вид:
Человек анализирует числовые данные такого рода и принимает решения. Знание температуры воздуха помогает правильно одеться. Курс валюты говорит покупать ее или продавать.
Когда значений одно или несколько, то никаких трудностей не возникает. Но когда значений десятки или сотни, то человеку сложно сразу понять, что означают полученные данные. На помощь приходят интегральные характеристики множеств значений и визуализация.
Одна из интегральных характеристик множества значений переменной величины – среднее арифметическое. Посмотрим на него с точки зрения статистики, физики (механики) и эстетики.
Среднее арифметическое двух чисел
Начнем с минимального набора чисел, для которых можно подсчитать среднее арифметическое. Вот два числа:
Их среднее арифметическое:
Физический смысл среднего арифметического
Изобразим два исходных числа и их среднее арифметическое на числовой оси:
Числа помечены черными кружками, а среднее арифметическое красным треугольником. Полученная конструкция – это весы. Для весов в равновесии правило рычага требует, чтобы моменты сил были равны. Весы не наклоняются ни в одну, ни в другую сторону, так как крутящий момент отсутствует.
В механике момент силы – это произведение силы F на расстояние l:
На плечи весов действует сила, создаваемая весом точек-«грузов». Обозначив расстояния от грузов до точки опоры l1 и l2, получим:
Точки-«грузы» отличаются только координатой на оси. Будем считать их вес одинаковым. Тогда:
Обозначив m координату точки опоры весов, получим:
Аналогично из формулы равенства моментов для произвольного количества N точек-«грузов» с одинаковым весом w выводится формула среднего арифметического. Равенство моментов для обоих плеч весов:
Координата опоры весов m:
Формула среднего арифметического дает координату точки опоры весов, находящихся в равновесии.
Визуальное восприятие равновесия
Равновесие в изобразительном искусстве играет важнейшую роль. Если при создании картины не достигнуто равновесие ее элементов, то произведение не будет законченным. В каждой картине художник создает равновесие различных визуальных сил.
Рудольф Арнхейм отмечает, что человеческое зрение способно обнаруживать малейшие отклонения от центра равновесия в изображении:
На приведенном примере слева круг находится в состоянии равновесия, а справа нет. Несмотря на то, что точка равновесия (центр квадрата) никак не отмечена на рисунке, человек с большой точностью может определить, находится ли круг в этой точке или нет.
Несмотря на то, что точка равновесия может быть не изображена, человек воспринимает ее как часть визуальной структуры:
Аналогично и среднее арифметическое: необязательно входит в набор чисел, но значимо для его восприятия и оценки.
Математическое ожидание случайной величины
Для случайной величины аналогом среднего арифметического служит математическое ожидание. Вероятность при этом можно считать весом точки-«груза». Формула равенства моментов с разными весами:
Теперь точка опоры весов в равновесии это μ:
Сумма всех вероятностей равна 1. Следовательно, и сумма весов равна 1. Тогда формула координаты точки весов в равновесии равна:
Это и есть формула математического ожидания.
Гистограмма
Гистограмма – это визуализация (геометрическое изображение) значений переменной величины с учетом вероятностей. Гистограмма показывает для выборки значений, какие из них появляются часто, какие реже, а какие совсем редко.
На гистограмме возможные значения откладываются по горизонтальной оси, а веса – по вертикальной. Диапазон значений по вертикали очевиден – от 0 до 1 (значения вероятности). По горизонтали диапазон должен включать ожидаемые значения переменной.
Гистограмма представляет собой простую картину (экземпляр изобразительного искусства). Зритель ожидает, что точка равновесия множества значений будет ровно посередине гистограммы:
Исходя из этого должен подбираться диапазон значений для горизонтальной оси гистограммы. Тогда сразу будет видно отклонение свойств выборки значений от ожидаемых:
Такого рода отклонение может быть вызвано выбросами. Выбросы – это значения, сильно отличающиеся от остальных. Благодаря правилу рычага, даже небольшое количество выбросов меняет точку равновесия и среднее арифметическое:
Дайте мне точку опоры, и я переверну Землю. Архимед
Общие сведения
Понятие среднеарифметической величины впервые предложил древнегреческий ученый — Пифагор. Позднее этот термин стал использоваться в математике. Чтобы понять его смысл, необходимо получить базовые знания о числовых значениях. Они делятся на 2 вида:
Первый тип — натуральные числа, они применяются при устном счете предметов.
Дробные бывают также двух типов:
Десятичные дроби делятся на конечные, периодические и непериодические бесконечные. Первый тип состоит из целой и дробной частей, разделенных между собой запятыми. Как правило, количество разрядов ограничено определенным значением. Если рассматривать бесконечные периодические десятичные дробные выражения, они состоят из множества элементов. Последние повторяются с определенной периодичностью. Например, 5,(321), где величина периода указывается в круглых скобках.
В случае когда дробное тождество является бесконечным непериодическим, очень часто представление осуществляется в форме обыкновенной дроби. Последняя состоит из делимого и делителя, отделенных друг от друга косой чертой «/». Первый элемент именуется числителем, а второй — знаменателем.
Обыкновенные дробные выражения бывают правильными, неправильными, а также могут записываться в форме смешанного числа, т. е. величины, состоящей из целого компонента и обыкновенной правильной дроби.
Перед подсчетом значения среднего арифметического в 5 классе специалисты рекомендуют ознакомиться с алгоритмом работы со смешанными величинами.
Смешанные числа
Смешанные числа являются промежуточными величинами между обыкновенными дробями и целыми. Не каждое дробное тождество можно представить в таком виде. Для этого подойдет только неправильное выражение. Алгоритм преобразования:
Методика обратной конвертации смешанного числа в неправильное дробное выражение является еще одной операцией, о которой нужно знать. Ее реализация:
Специалисты рекомендуют начинающему математику потренироваться, придумывая различные задания на конвертацию числовых выражений.
Далее необходимо перейти непосредственно к определению, позволяющему расшифровать, что значит среднее арифметическое чисел, а также к самой методике расчета искомой величины.
Алгоритм нахождения среднего значения
Среднее арифметическое — математическая характеристика, позволяющая найти оптимальное значение.
Например, на уроках выставляется оценка за месяц. Для ее вычисления необходимо найти среднее значение всех отметок, полученных учеником.
Кроме того, среднее арифметическое используется при вычислении какой-либо характеристики опытным путем.
Например, при расчете заряда электрона производится определенное количество измерений, а затем рассчитывается средняя величина заряда частицы.
Методика определения среднеарифметического значения:
Для реализации алгоритма на практике необходимо записать несколько чисел — 4, 7, 8, 12, 15. Решение выглядит следующим образом:
В некоторых случаях результат необходимо округлять. Однако этого можно не делать при подсчете какой-либо физической величины.
При проведении опытов необходимо брать больше значений, поскольку это существенно влияет на точность получения данных.
Пример решения
Для закрепления теории необходимо разобрать пример и решить его. Например, нужно найти среднее арифметическое четырех смешанных чисел, а именно: 3 2/3, 4 5/7 и 6 3/8.
Решение выполняется по следующему алгоритму:
При получении результата в виде неправильной дроби, его нужно преобразовать в смешанную величину. Это считается «правилом хорошего тона» в математике, поскольку любой ответ должен переводиться в читабельную сокращенную форму.
Кроме того, можно проверить результат выполнения операции, воспользовавшись онлайн-сервисами. Однако пользоваться ими часто не рекомендуется, поскольку нужно уметь искать ошибки самостоятельно.
Таким образом, для вычисления среднеарифметического значения необходимо знать специальную методику, предложенную специалистами в области математики.
Среднее арифметическое
Среднее арифметическое – это частное от деления суммы чисел на их количество.
Пример 1. Найти среднее арифметическое двух чисел: 4 и 6.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых, то есть на 2:
Значит среднее арифметическое двух чисел (4 и 6) равно 5.
Пример 2. Найти среднее арифметическое чисел 15, 8, 20 и 13.
Решение: Сначала найдём сумму данных чисел:
Затем разделим полученный результат на количество слагаемых:
Из данных примеров можно сделать вывод, что для нахождения среднего арифметического, нужно сложить все числа и поделить их сумму на их количество.
Рассмотрим задачи, в которых требуется найти средне арифметическое нескольких чисел, относящихся к одной величине.
Задача 1. Утром температура была 15 градусов, днём она поднялась до 27 градусов, а вечером опустилась до 19, ночью температура достигла отметки в 11 градусов. Найти среднюю температуру за сутки.
Решение: Сначала найдём общую сумму температур за сутки:
15 + 27 + 19 + 11 = 72,
затем разделим полученную сумму на 4:
Ответ: средняя температура за сутки равна 18 градусам.
Задача 2. В магазине продали 6 килограммов яблок по цене 55 рублей за килограмм и 4 килограмма груш по цене 75 рублей за килограмм. Какая средняя цена 1 килограмма фруктов?
Решение: Сначала посчитаем сколько всего денег получил магазин за фрукты:
55 · 6 = 330 (р) — выручка за яблоки;
75 · 4 = 300 (р) — выручка за груши;
330 + 300 = 630 (р) — общая выручка за фрукты.
Затем найдём общий вес фруктов:
теперь разделим общую выручку на общий вес проданных фруктов и получим среднюю цену за 1 кг:
Ответ: средняя цена 1 килограмма проданных фруктов — 63 рубля.
Среднее арифметическое
Предложена (наряду со средним геометрическим и средним гармоническим) ещё пифагорейцами.
Частными случаями среднего арифметического являются среднее (генеральной совокупности) и выборочное среднее (выборки).
При стремлении количества элементов множества чисел стационарного случайного процесса к бесконечности среднее арифметическое стремится к математическому ожиданию случайной величины.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Центра́льные преде́льные теоре́мы (Ц. П. Т.) — класс теорем в теории вероятностей, утверждающих, что сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
В теории вероятностей два случайных события называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. Аналогично, две случайные величины называют независимыми, если известное значение одной из них не дает информации о другой.
Пропорциональными называются две взаимно зависимые величины, если отношение их значений остаётся неизменным.
В теории вероятностей случайная величина имеет дискретное равномерное распределение, если она принимает конечное число значений с равными вероятностями.
Для определения средних или наиболее типичных значений совокупности используются показатели центра распределения. Основные из них — математическое ожидание, среднее арифметическое, среднее геометрическое, среднее гармоническое, среднее степенное, взвешенные средние, центр сгиба, медиана, мода.