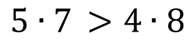Что значит сравнить выражения

Числовые и буквенные выражения

Числовые выражения

В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.

Значение выражения — это результат выполненных действий.

Чтение числовых выражений

Решение числовых выражений

45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13

Сравнение значений числовых выражений

Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.

Для этого найдем значения каждого из них:

Буквенные выражения

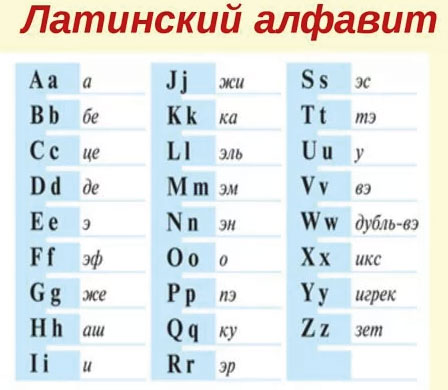
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.

Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.

Чаще всего используются буквы:

a, b, c, d, x, y, k, m, n

Алгоритм решения буквенного выражения

1. Прочитать буквенное выражение

2. Записать буквенное выражение

3. Подставить значение неизвестного в выражении

4. Вычислить результат

Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с

Подставим вместо неизвестного «с» число 4.

У нас получается выражение: 28 – 4

Переменные

Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.

Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства

Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:

Теперь мы можем найти значение этого выражения:

с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7

Поделись с друзьями в социальных сетях:

Источник

Сравнение значений выражений

Урок 3. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Сравнение значений выражений»

· разобрать, каким образом сравнивают выражения;

· показать что такое двойное неравенство;

· ввести понятия «строгое неравенство», «нестрогое неравенство».

Прежде, чем приступить к рассмотрению новой темы, вспомним, что:

Например, выражение 10(2 + 1,5) является числовым.

Выполнив действия этого числового выражения, соблюдая правильный порядок действий, получим число 35, которое называют значением данного числового выражения.

А теперь, чтобы разобраться, каким образом сравнивают значения выражений, решим следующую задачу.

Результат сравнения можно записать в виде следующего неравенства:

Таким образом, для любых двух числовых выражений можно установить, равны их значения или не равны. Если они не равны, то можем определить, какое из них больше и какое меньше.

Мы разобрались, как сравнить два числовых выражения. А как же быть с выражениями, содержащими переменные.

Давайте сравним значения выражений:

Видим, что для разных значений переменных результат сравнения выражений с переменными может оказаться различным.

Иногда перед нами может встать задача установить, между какими числами заключено значение выражения.

Источник

Математика. 2 класс

Конспект урока

Математика, 2 класс

Урок № 14. Числовые выражения. Порядок действий в числовых выражениях. Скобки. Сравнение числовых выражений

Перечень вопросов, рассматриваемых в теме:

— Что такое числовые выражения?

— Как правильно читать и записывать числовые выражения?

— Как выполнять порядок действий, если есть скобки?

— Как сравнить два выражения?

Числовое выражение – это запись, состоящая из чисел и знаков действий между ними.

Значение выражения – это результат выполненных действий.

Сравнить числовые выражения – найти значение каждого из выражений и их сравнить.

Порядок выполнения действий – это последовательность проводимых вычислений в данном выражении.

Основная и дополнительная литература по теме:

1. Моро М. И., Бантова М. А., Бельтюкова Г. В.и др. Математика. 2 класс. Учебник для общеобразовательных организаций. В 2 ч. Ч.1. –8-е изд. – М.: Просвещение, 2017. – с.38-40

2. Волкова А. Д. Математика. Проверочные работы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, 2017, с. 22-27

3. Глаголева Ю. И., Волкова А. Д. Математика. КИМы. 2 кл: учебное пособие для общеобразовательных организаций. М.: Просвещение, Учлит, 2017, с.16

Теоретический материал для самостоятельного изучения

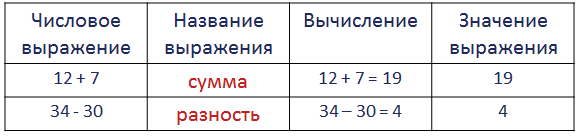
Маша и Миша решали пример: из числа 12 вычесть сумму чисел 7 и 3. Они записали его по-разному и получили разные ответы. Маша сначала из 12 вычла 7 и получила 5, потом прибавила 3, получила 8.

Миша обвёл овалом сумму чисел 7 и 3 и сначала посчитал сумму, получил 10. Затем от 12 отнял 10, получил 2.

Кто из них вычислил верно? Решил верно, Миша.

Запишем пример, который решали дети правильно:

Вычислим. 7 + 3 равно 10, из 12 вычесть 10, получится 2. Запомните: действия, записанные в скобках, выполняются первыми.

Посмотрим на запись.

Запись, в которой разные числа (однозначные и двузначные) соединены знаками «+» и «–» в различных сочетаниях, называется числовым выражением и читается так: «из числа 9 вычесть сумму чисел 6 и 2».

Найти значение выражения – это значит, нужно выполнить все указанные действия в выражении. Значение данного выражения 1.

Теперь мы будем называть примеры числовыми выражениями, а ответы значениями числовых выражений.

К числу 10 прибавить разность чисел 8 и 3.

Как найти значение выражения? Нужно выполнить необходимые действия. Но с какого действия нужно начинать? С того, которое записано в скобках. Находим разность чисел 8 и 3, будет 5, к 10 прибавить 5, получится 15.

Давайте сравним значения двух выражений:

Сначала найдем значение каждого из выражений и их сравним.

Источник

1.1. Методы сравнения. числовых выражений

При сравнении числовых выражений AИ BИспользуют следующие общие методы.

Метод сравнения с нулем
разности выражений

В этом случае сравнивают разность выражений с нулем.

Метод сравнения с единицей
отношения выражений

Если выражения AИ BПоложитель­ны, то для определения большего из них можно сравнить их отношение с едини­цей.

22012+1 22013+1

Метод разделения выражений

Если удается показать, что одно из сравниваемых выражений А больше не­которого числа (или выражения) С, а второе В наоборот меньше него, то пер­вое выражение будет больше второго, т. е. из неравенств A>C>BСледует нера­венство A>B.

Решение. Заметим, что log25 >>log24 = 2, а log36 2 >log3 6 «• log2 5 >log3 6.

Метод использования параметра

Так как A ≠ B, то (A— B)2>0 и тогда V60 >2 + 3/7.

Метод использования свойств функций

В этом случае для сравнения выраже­ний используют монотонность или вы­пуклость функций на промежутках.

Рассмотрим функцию F (X)=

Всей области определения.

Графический метод удобно использо­вать при сравнении двух выражений, ко­торые частично одинаковы (равные пока­затели степеней, равные основания сте­пеней, равные показатели корней, равные подкоренные числа, равные основания логарифмов, равные подлогарифмиче­ские числа и т. д.).

Пример 6. Сравнить числаLog36 И Log46.

Решение. Построим схематично гра­

Фики функций Y = log3XИ Y = log4X(см.

Метод использования
классических неравенств

Обычно достаточно знания следую­щих классических неравенств:

Неравенство между средним арифме­тическим и средним геометрическим неотрицательных чисел A1И A2(слу­чай N = 2 в неравенстве Коши):

Неравенство для суммы двух взаимно обратных чисел:

Решение. а) Заметим, что log5 2 >0 и

Log2 5 log5 2 log5 2

Выражение в правой части равенства представляет собой сумму обратных положительных ных от единицы. Значит,

Двух взаимно
чисел, отлич-

Б) Возводя оба числа в двухсотую сте­пень, получим:

2002 v 1,005 ^ 2 v (1,005)200.

Используя неравенство Бернулли, имеем:

(1,005)200 = (1 + 0,005)200>1 + 200 ∙ 0,005 = 2.

Значит второе число больше первого.

1.2. Сравнение действительных чисел

При сравнении действительных чисел используют следующие правила.

• Всякое положительное число боль­ше нуля и больше отрицательного числа.

• Всякое отрицательное число меньше нуля.

• Из двух положительных действи­тельных чисел больше то, у которого це­лая часть больше. Если целые части рав­ны, большим считается то число, у кото­рого первый из неравных десятичных знаков в их записи в виде десятичной дроби больший, а все предшествующие одинаковы.

• Из двух отрицательных чисел боль­ше то, у которого абсолютная величина меньше.

Замечание. Данный пример приведен для раскрытия правила сравнения дейст­вительных чисел, записанных в виде бес­конечных десятичных дробей до опреде­ленного знака.

1.3. Сравнение выражений,
содержащих дроби

При сравнении двух обыкновенных дробей используют следующие правила.

• Из двух дробей с одинаковыми зна­менателями та дробь больше, у кото­рой больший числитель.

• Из двух дробей с одинаковыми чис­лителями та дробь больше, у которой знаменатель меньше.

При сравнении двух обыкновенных дробей с разными числителями и знаме­нателями их можно привести к общему знаменателю (или умножить обе части сравнения на общий знаменатель).

Решение. Приводя дроби к общему

Знаменателю и используя первое прави­ло, получаем

Источник

Сравнение выражений

Вначале рассматривается сравнение чисел с опорой на множества, и результат фиксируется с помощью знаков «больше», «меньше», «равно». После этого дети сравнивают число и выражение, найдя значение выражения, сравнивают его с данным числом.

Например, 5 ∙ 3 + 4, 5 ∙ 5 – 2. Желательно давать не только готовые выражения, но и составлять их, используя предметные действия с множествами. На третьем этапе дети сравнивают два выражения вида 10 – 5 и 3 + 4; 8 – 3 и 8 – 4. В таких выражениях сравнение можно производить не только нахождением их значений, но и наблюдением за компонентами действия. (Чем большее число мы отнимем от одного и того же числа, тем меньше будет остаток).

Работа по сравнению выражений и составлению верных равенств часто связана с преобразованием выражений на основе изучаемых свойств:

При сравнении выражений дети знакомятся с терминами «равенство» и «неравенство», которые могут быть верными или неверными.

В программе «Школа 2000» алгебраический материал не только связан с арифметическим материалом, но и является материалом для развития учащихся. Он намного богаче содержанием и вводится с первого класса.

Как и в традиции, составляются выражения (по рисункам), причем не только числовые, но и буквенные:

П + К а + б a + б = к, к – а = б

Рано вводятся термины «равенство», «неравенство», «выражение».

Сравнение выражений основано на рассуждении:

Правила о порядке выполнения действий рассматриваются с точки зрения алгоритмов (т.е. составление программ).

Для закрепления правил выполняются такие упражнения

1) расставь скобки по заданной программе;

2) составь выражения по схеме-«дереву»;

3) составь программу действий в выражении

Выражение с переменной

Подготовительная работа заключается в решении задач с недостающими данными, например: Купили несколько дневников по пять рублей. Сколько заплатили за дневники?

Выражения с переменной очень широко используются для обобщения знаний:

1) Все законы и свойства записываются в общем виде:

2) Решения задач (из блиц-турниров) записываются в общем виде, с буквенными данными:

3) Вводятся условные обозначения величин и их формулы:

Вопрос 20. Формирование представлений об уравнении. Методика обучения решению уравнений и задач, решаемых уравнением.

В начальной школе рассматриваются уравнения, содержащие только одно действие. Первоначально они решаются подбором. В дальнейшем уравнения решаются на основе зависимости между компонентами и результатами действий.

В традиционной школе уравнения вводятся во втором классе, а в других системах – с начала обучения. Дети знакомятся с терминами «уравнение» и «решение уравнения». Для закрепления этих понятий предлагаются упражнения: «Выбери среди данных записей уравнения», «Преврати (составь) уравнения». Кроме этого включаются задания такого вида:

«Угадай корни: 7 + х = 7; 7 – у = 0; n – 0 = 7; а – а = 7; b – b = 0».

В «Школе 2000» уравнения вводятся в 3 части 1 класса. Вначале выполняются привычные операции с множествами-«мешками»:

и вводится термин «уравнение».

Опорой для решения уравнений являются понятия части и целого. В течение подготовительного периода учащиеся осваивают эти понятия в операциях с множествами и усваивают их соотношения: чтобы найти одну часть надо от целого отнять другую часть.

Последовательность введения уравнений такая же, как и в традиционной программе, но на одном уроке при закреплении могут встречаться уравнения разных видов, т.к. основа их решения похожа.

Помощниками в решении уравнениях являются:

1) рисунки весов 2 + х = 4

2) схемы 5 – х = 4 х + 3 = 7

3) числовые отрезки

4) уравнения с линиями

Кроме уравнений на нахождение части и целого, включены нестандартные уравнения:

Основой для их решений является зависимость между сторонами прямоугольника и его площадью: чтобы найти сторону

В 3 кл. происходит обобщение знаний по уравнениям: вводится термин „уравнение“, „решение уравнения“ и рекомендуется решать их с комментированием:

1. Неизвестное делимое х+3. Чтобы найти …

При изучении дробей включены уравнения

,которые решаются аналогично.

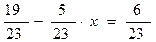
В системе РОЗ (М1А, стр. 19) вводятся термины «равенства», «неравенства», с помощью рисунков составляются верные равенства и неравенства. Неверные неравенства превращаются в верные.

х + 5 = 9, которые вводятся через задачу.

Уравнения могут быть не стандартными:

( 5 + х ) + 2 = 11,где надо догадаться при сравнении равенств,

( 5 + 4 ) + 2 = 11,чему равно неизвестное.

В конце первого класса, дети знакомятся с уравнениями вида:

Все виды этих уравнений даются в сравнении друг с другом:

надо выяснить связь этих уравнений и тогда найти решение.

Во втором классе продолжается работа над уравнениями, где надо найти самое большое число и воспользоваться обратными действиями:

а + 23 = 41 85 – к = 72

Уравнения, связанные с действиями умножения и деления решаются с помощью таблицы умножения (подбором).

Для решения уравнений другим способом изучаются основные свойства равенств:

1) а = b, ó a + c = b + c, ó a– c = b – c.

5 у + 7 = 62 5у + 7 = 62

Вопрос 21. Методика изучения геометрического материала в начальной школе.

Математическое развитие школьников невозможно без приобщения их к геометрии. В начальных классах ставится задача расширить и уточнить представления учащихся о геометрических фигурах, а также развивать их пространственное мышление в процессе выполнения различных практических упражнений.

Для осуществления методической работы, направленной на решение этих задач, учителю необходимо знать, что геометрия как наука строится на базе основных понятий и аксиом, а новые факты вводятся дедуктивным путем. Школьный курс геометрии – это евклидова геометрия на плоскости и в пространстве. Эта геометрия опирается на понятие величины и ее измерения. Формирование представлений о геометрических фигурах в начальной школе связано с изучением длины и площади.

Основой формирования представлений о геометрических фигурах явля­ется способность детей воспринимать форму предмета. Эта способность позво­ляет узнавать, различать и изображать различные геометрические фигуры:

Основными геометрическими фигурами, изучаемыми в начальной школе, являются: точка, прямая и кривая линии, отрезок и ломаная, а затем угол, прямоугольник, квадрат, многоугольник, треугольник.

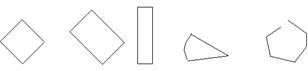Чтобы дети имели представление об этих фигурах, их достаточно показать и назвать термином (остенсивное определение). Но ученик воспринимает фигуру как целостный объект и не выделяет свойства объекта, поэтому не всегда узнает знакомые фигуры, расположенные необычно:

«не «не квадрат» «не прямоугольник» «треугольник» «многоугольник»

В дальнейшем необходимо изучать существенные свойства объектов для точных представлений о них. Для этой цели геометрические фигуры изучают в определенной последовательности, выполняя с моделями различные практические действия.

Точка— след карандаша, ручки, мела. Через точку дети проводят различные линии: прямые и кривые. Убеждаются, что через точку можно провести сколько угодно прямых и кривых, а через две точки – только одну прямую и множество кривых.

Отрезок – это часть прямой между двумя ее точками. Отрезок имеет начало и конец, любая его точка может быть и концом и началом. Отрезок имеет длину. Отрезки можно сравнивать, складывать и отнимать, измерять.

Ученику начальных классов трудно различать такие понятия как «прямая» и «отрезок» и идти к пониманию отрезка от прямой. В просторечии слово «отрезок» почти не употребляется, говорят: «прямая», «идти по прямой», но при этом никто не имеет в виду бесконечную прямую, как принято в геометрии. Бесконечную прямую нельзя изобразить на бумаге. В учебниках математики для начальной школы принято при изображении отрезка отмечать его начало и конец точками или штрихами, чего нет в изображении прямой.

Угол можно ввести как фигуру, образованную двумя лучами, исходящими из одной точки. Такой подход к введению понятия угла возможен там, где вводится понятие луча, как части прямой, имеющей начало, но не имеющей конца. (например, М1А). В учебнике М2П углом называют часть плоскости, заключенной между двумя лучами, исходящими из одной точки, причем называют меньшую часть, т.к. плоскость делится лучами на две части.

Источник