Что значит сравнить выражения по математике 4 класс
Сравнение выражений
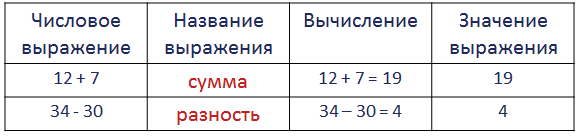
Вначале рассматривается сравнение чисел с опорой на множества, и результат фиксируется с помощью знаков «больше», «меньше», «равно». После этого дети сравнивают число и выражение, найдя значение выражения, сравнивают его с данным числом.
Например, 5 ∙ 3 + 4, 5 ∙ 5 – 2. Желательно давать не только готовые выражения, но и составлять их, используя предметные действия с множествами. На третьем этапе дети сравнивают два выражения вида 10 – 5 и 3 + 4; 8 – 3 и 8 – 4. В таких выражениях сравнение можно производить не только нахождением их значений, но и наблюдением за компонентами действия. (Чем большее число мы отнимем от одного и того же числа, тем меньше будет остаток).
Работа по сравнению выражений и составлению верных равенств часто связана с преобразованием выражений на основе изучаемых свойств:
При сравнении выражений дети знакомятся с терминами «равенство» и «неравенство», которые могут быть верными или неверными.
В программе «Школа 2000» алгебраический материал не только связан с арифметическим материалом, но и является материалом для развития учащихся. Он намного богаче содержанием и вводится с первого класса.
Как и в традиции, составляются выражения (по рисункам), причем не только числовые, но и буквенные:
П + К а + б a + б = к, к – а = б
Рано вводятся термины «равенство», «неравенство», «выражение».
Сравнение выражений основано на рассуждении:
Правила о порядке выполнения действий рассматриваются с точки зрения алгоритмов (т.е. составление программ).
Для закрепления правил выполняются такие упражнения
1) расставь скобки по заданной программе;
2) составь выражения по схеме-«дереву»;
3) составь программу действий в выражении
Выражение с переменной
Подготовительная работа заключается в решении задач с недостающими данными, например: Купили несколько дневников по пять рублей. Сколько заплатили за дневники?
Выражения с переменной очень широко используются для обобщения знаний:
1) Все законы и свойства записываются в общем виде:
2) Решения задач (из блиц-турниров) записываются в общем виде, с буквенными данными:
3) Вводятся условные обозначения величин и их формулы:
Вопрос 20. Формирование представлений об уравнении. Методика обучения решению уравнений и задач, решаемых уравнением.
В начальной школе рассматриваются уравнения, содержащие только одно действие. Первоначально они решаются подбором. В дальнейшем уравнения решаются на основе зависимости между компонентами и результатами действий.
В традиционной школе уравнения вводятся во втором классе, а в других системах – с начала обучения. Дети знакомятся с терминами «уравнение» и «решение уравнения». Для закрепления этих понятий предлагаются упражнения: «Выбери среди данных записей уравнения», «Преврати (составь) уравнения». Кроме этого включаются задания такого вида:
«Угадай корни: 7 + х = 7; 7 – у = 0; n – 0 = 7; а – а = 7; b – b = 0».
В «Школе 2000» уравнения вводятся в 3 части 1 класса. Вначале выполняются привычные операции с множествами-«мешками»:
и вводится термин «уравнение».
Опорой для решения уравнений являются понятия части и целого. В течение подготовительного периода учащиеся осваивают эти понятия в операциях с множествами и усваивают их соотношения: чтобы найти одну часть надо от целого отнять другую часть.
Последовательность введения уравнений такая же, как и в традиционной программе, но на одном уроке при закреплении могут встречаться уравнения разных видов, т.к. основа их решения похожа.
Помощниками в решении уравнениях являются:
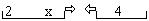
2) схемы 5 – х = 4 х + 3 = 7
3) числовые отрезки
4) уравнения с линиями
Кроме уравнений на нахождение части и целого, включены нестандартные уравнения:
Основой для их решений является зависимость между сторонами прямоугольника и его площадью: чтобы найти сторону
В 3 кл. происходит обобщение знаний по уравнениям: вводится термин „уравнение“, „решение уравнения“ и рекомендуется решать их с комментированием:
1. Неизвестное делимое х+3. Чтобы найти …
При изучении дробей включены уравнения
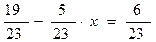
В системе РОЗ (М1А, стр. 19) вводятся термины «равенства», «неравенства», с помощью рисунков составляются верные равенства и неравенства. Неверные неравенства превращаются в верные.
х + 5 = 9, которые вводятся через задачу.
Уравнения могут быть не стандартными:
( 5 + х ) + 2 = 11,где надо догадаться при сравнении равенств,
( 5 + 4 ) + 2 = 11,чему равно неизвестное.
В конце первого класса, дети знакомятся с уравнениями вида:
Все виды этих уравнений даются в сравнении друг с другом:
надо выяснить связь этих уравнений и тогда найти решение.
Во втором классе продолжается работа над уравнениями, где надо найти самое большое число и воспользоваться обратными действиями:
а + 23 = 41 85 – к = 72
Уравнения, связанные с действиями умножения и деления решаются с помощью таблицы умножения (подбором).
Для решения уравнений другим способом изучаются основные свойства равенств:
1) а = b, ó a + c = b + c, ó a– c = b – c.
5 у + 7 = 62 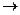
Вопрос 21. Методика изучения геометрического материала в начальной школе.
Математическое развитие школьников невозможно без приобщения их к геометрии. В начальных классах ставится задача расширить и уточнить представления учащихся о геометрических фигурах, а также развивать их пространственное мышление в процессе выполнения различных практических упражнений.
Для осуществления методической работы, направленной на решение этих задач, учителю необходимо знать, что геометрия как наука строится на базе основных понятий и аксиом, а новые факты вводятся дедуктивным путем. Школьный курс геометрии – это евклидова геометрия на плоскости и в пространстве. Эта геометрия опирается на понятие величины и ее измерения. Формирование представлений о геометрических фигурах в начальной школе связано с изучением длины и площади.
Основой формирования представлений о геометрических фигурах является способность детей воспринимать форму предмета. Эта способность позволяет узнавать, различать и изображать различные геометрические фигуры:
Основными геометрическими фигурами, изучаемыми в начальной школе, являются: точка, прямая и кривая линии, отрезок и ломаная, а затем угол, прямоугольник, квадрат, многоугольник, треугольник.
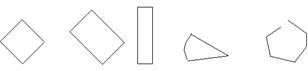 |
Чтобы дети имели представление об этих фигурах, их достаточно показать и назвать термином (остенсивное определение). Но ученик воспринимает фигуру как целостный объект и не выделяет свойства объекта, поэтому не всегда узнает знакомые фигуры, расположенные необычно:
«не «не квадрат» «не прямоугольник» «треугольник» «многоугольник»
В дальнейшем необходимо изучать существенные свойства объектов для точных представлений о них. Для этой цели геометрические фигуры изучают в определенной последовательности, выполняя с моделями различные практические действия.
Точка— след карандаша, ручки, мела. Через точку дети проводят различные линии: прямые и кривые. Убеждаются, что через точку можно провести сколько угодно прямых и кривых, а через две точки – только одну прямую и множество кривых.
Отрезок – это часть прямой между двумя ее точками. Отрезок имеет начало и конец, любая его точка может быть и концом и началом. Отрезок имеет длину. Отрезки можно сравнивать, складывать и отнимать, измерять.
Ученику начальных классов трудно различать такие понятия как «прямая» и «отрезок» и идти к пониманию отрезка от прямой. В просторечии слово «отрезок» почти не употребляется, говорят: «прямая», «идти по прямой», но при этом никто не имеет в виду бесконечную прямую, как принято в геометрии. Бесконечную прямую нельзя изобразить на бумаге. В учебниках математики для начальной школы принято при изображении отрезка отмечать его начало и конец точками или штрихами, чего нет в изображении прямой.
Угол можно ввести как фигуру, образованную двумя лучами, исходящими из одной точки. Такой подход к введению понятия угла возможен там, где вводится понятие луча, как части прямой, имеющей начало, но не имеющей конца. (например, М1А). В учебнике М2П углом называют часть плоскости, заключенной между двумя лучами, исходящими из одной точки, причем называют меньшую часть, т.к. плоскость делится лучами на две части.
Числовые и буквенные выражения
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).
Числовые выражения: что это
Числовое выражение — это запись, которая состоит из чисел и знаков арифметического действия между ними.
Именно числовые выражения окружают нас повсюду — не только на уроках математики, но и в магазине, на кухне или когда мы считаем время. Простые примеры, в которых нужно вычислить разность, сумму, получить результат умножения или деления — это все числовые выражения.
Например:
Это простые числовые выражения.
Чтобы получить сложное числовое выражение, нужно к простому выражению присоединить знаком арифметического действия еще одно простое числовое выражение. Вот так:
Это сложные числовые выражения.
Знать, где простое выражение, а где сложное — нужно, но называть оба типа выражений следует просто «числовое выражение».
Число, которое мы получаем после выполнения всех арифметических действий в числовом выражении, называют значением этого выражения.
Вспомним, какие виды арифметических действий есть.
+ — знак сложения, найти сумму.
— — знак вычитания, найти разность.
* — знак умножения, найти произведение.
: — знак деления, найти частное.
11 — значение числового выражения.
6 * 8 = 48
48 — значение числового выражения.
При вычислении сложных числовых выражений нужно строго соблюдать очередность выполнения арифметических действий:
Онлайн-курсы математики для детей помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.
Пример 2. Найдите значение числового выражения: (6 + 7) * (13 + 2)
Часто бывает нужно сравнить два числовых выражения.
Сравнить числовые выражения — значит найти значения каждого выражения и сравнить их.
Пример 1. Сравните два числовых выражения: 6 + 8 и 2 * 2
14 больше 4
14 > 4
6 + 8 > 2 * 2
Буквенные выражения
Кажется, с числовыми выражениями все достаточно просто. Буквенные выражения немногим сложнее.
В буквенном выражение есть цифры, знаки арифметических действия и буквы.
Получается, что буквенное выражение — это числовое выражение, в котором есть не только числа, но и буквы.
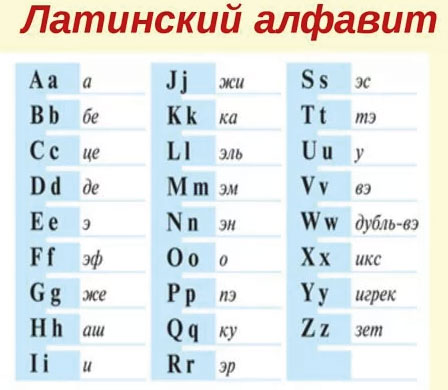
Это буквенные выражения. Для записи буквенных выражений используют буквы латинского алфавита.
У буквенных выражений, как и у числовых, есть определенный алгоритм вычисления:
Пример 1. Найдите значение выражения: 5 + x.
Пример 2. Найдите значение выражения: (4 + a) * (2 + x).
Выражения с переменными
Переменная — это значение буквы в буквенном выражении.
Числа, которые подставляют вместо переменных — это значения переменных. В нашем примере это числа 5 и 10.
Число и переменная записаны без знака арифметического действия. Так коротко записывается умножение.
5x — это произведение числа 5 и переменной x
4a — это произведение числа 4 и переменной a
Числа 4 и 5 называют коэффициентами.
Коэффициент показывает, во сколько раз будет увеличена переменная.
Теперь вы вооружены всеми необходимыми теоретическими знаниями о числовых и буквенных выражениях. Давайте немного поупражняемся в решении задачек и примеров, чтобы научиться применять полученные знания на практике.
Задание раз.
Задание два.
Составьте буквенное выражение:
Сумма разности b и 345 и суммы 180 и x.
Ответ: роллы “Калифорния” и “Филадельфия” вместе стоят 1 000 рублей.
Задание пять.
Составьте выражение для решения задачи и найдите его значение.
Маша посмотрела за день 150 видео в ТикТок, а Лена — на 13 видео больше. Сколько всего видео было просмотрено обеими девочками?
150 + (150 + 13)
Выполняем сначала действие в скобках: 150 + 13 = 163.
150 + 163 = 313.
Ответ: Маша и Лена посмотрели всего 313 видео.
Конспект урока по математике » Сравнение числовых выражений»
Выполнила учитель начальных классов : Нечаева А.А.
Тип урока: открытие новых знаний.
Сравнение числовых выражений.
Числовые выражения. Значение выражения. Сравнение выражений. Компоненты действий сложения и вычитания.
Основные : Учебник М.И. Моро «Математика. 2 класс», тетрадь на печатной основе «Математика. 2 класс, ч. 1»М.И.Моро, С.И. Волкова.
Дополнительные : тетради, карточки с заданиями, листы оценки.
Фронтальная работа, индивидуальная работа, работа в парах.
Обучение сравнению числовых выражений.
Учить сравнивать числовые выражения, оформлять доказательства рассуждений.
Совершенствовать вычислительные навыки и умение решать задачи.
Воспитывать культуру поведения при фронтальной работе, индивидуальной работе, работе в парах.
Воспитывать интерес к предмету, аккуратность и точность в работе.
Развивающие: формировать УУД:
Личностные: определять и высказывать самые простые и общие для всех людей правила поведения; устанавливать связь между учебной деятельностью и её мотивом.
Общеучебные: уметь самостоятельно выделять и формулировать познавательную цель, структурировать знания, выбирать способы решения задач, контролировать и оценивать процесс и результат учебной деятельности.
Знаково-символические: моделирование и преобразование моделей.
Логические: анализировать объекты, осуществлять синтез из частей, выбирать критерии для классификации; устанавливать причинно-следственные связи.
Постановка и решение проблем: учить формулировать проблему, самостоятельно создавать способы её решения.
Регулятивные: учить планировать свою деятельность, прогнозировать результат, осуществлять самооценку и саморегуляцию.
Коммуникативные: планировать учебное сотрудничество совместно с учителем; ставить вопросы, разрешать конфликты, уметь с достаточной полнотой и точностью выражать свои мысли.
Личностные : формирование внутренней позиции школьника, самоуважение и самооценка; морально-этическая ориентация.
Предметные : владение понятиями «выражение», «значение выражений», умением составлять, записывать и сравнивать выражения.
Регулятивные: управление своей деятельностью, инициативность и самостоятельность.
Коммуникативные: владение речевой деятельностью, навыки сотрудничества.
Познавательные: умение работать с информацией, работать с учебными моделями, выполнять логические операции( сравнение, синтез, анализ, классификация), использование знаково-символических средств.
устанавливать связь между учебной деятельностью и её мотивом
Сегодня У нас на уроке гости. Мы все немного волнуемся, но настроены на работу.
Приветствуют гостей в классе
( прикладывают ладони к области сердца, протягивают ладони друг другу и гостям), усаживаются на места, готовятся к работе.
Актуализация опорных знаний.
Воспитывать культуру поведения при фронтальной работе, индивидуальной работе.
Анализировать объекты, осуществлять синтез из частей, выбирать критерии для классификации; устанавливать причинно-следственные связи.
учить формулировать проблему, самостоятельно создавать способы её решения.
На дворе осень… С деревьев облетают последние листья. Некоторые из них оказались у нас в классе и устроили небольшой математический листопад. Они очутились у вас на партах и принесли с собой задания. Те ребята, у кого на партах есть кленовые листочки, начинают решать примеры, записанные на них. Ответы пишите прямо в карточку.
А вот и ещё листья! Я приготовила для вас отрезок числового ряда, но листья, кружась по классу, закрыли некоторые числа.
Назовите число, в котором количество десятков больше количества единиц на 2.
Число, которое при счёте предшествует числу 29
Число, которое при счёте следует за числом 25
Про какое число можно сказать, что в его составе только круглые десятки?
Ребята, работая с отрезком числового ряда, что именно мы повторяли?
Молодцы, вы легко справились с заданием. Думаю, что вам по силам будет следующее задание.
Вспомните, что мы называем выражением? Что значит найти значение выражения?
Сравнение натуральных чисел
Вам уже известно, что натуральные числа используются для обозначения количества тех или иных предметов. Возьмем, к примеру, конфеты. Мама купила шоколадные батончики и высыпала их кучкой на столе. Дети пересчитали, и их оказалось 25 штук.
Пришел с работы папа и высыпает рядом еще конфеты. На первый взгляд, эта кучка не отличается от первой, но пересчитав количество папиных конфет, дети увидели, что их всего 23. Значит, эти кучки разные. Чтобы это выяснить, дети произвели два действия:
Сравнить натуральные числа – это означает узнать, отличаются ли они друг от друга или они одинаковые. Если сравниваемые числа отличаются, тогда мы может узнать, что одно число больше другого, а второе, соответственно, меньше первого.
Как сравнить натуральные числа
Сравнить натуральные числа можно такими способами:
В результате сравнения мы можем получить:
Равенство натуральных чисел
Если два натуральных числа имеют полностью одинаковую запись, то и записанные с их помощью числа одинаковы (говорят просто – они равны). Если их записи отличаются, тогда эти числа не равны.
Если мы определили, что числа не равны, тогда нам необходимо выяснить, какое положение они занимают по отношению друг к другу, большее или меньшее.
Запись и чтение неравенств
Неравенство – это запись чисел или математических выражений, которая содержит знаки неравенства.
Читается подобная запись следующим образом. Первое число называется в именительном падеже (кто? что?), а второе в родительном (кого? чего?). Например, так: «два меньше четырех», «восемьдесят девять больше семидесяти восьми».
Если стрелка смотрит влево: « меньше » и означает, что слева от него находится число меньшее, чем справа.
Если стрелка смотрит вправо: «>», такой знак называется « больше » и означает, что слева от него находится большее число, чем справа.
Стрелка знака всегда указывает на меньшее число, а двойная вилка – на большее!
Например, дано неравенство 5 верным (правильно отмеченным), например, 1 неверным (неправильно отмеченным), например, 5>6.
Сравнение однозначных натуральных чисел с помощью ряда
Этот способ лучше всего подходит для сравнения однозначных натуральных чисел.
Меньшим называют число, которое в натуральном ряду находится раньше другого, а большим – то, которое расположено позже другого.
Например, число 2 в натуральном ряду стоит раньше, чем число 4, значит, 2 8.
Число 1 (единица) – самое меньшее из натуральных чисел, поскольку стоит в натуральном ряду первым.
На координатном луче меньшее число обозначается раньше (левее), а большее число – позже (правее) другого числа.
Рис. 1. Большее и меньшее число на координатном луче.
Действительно, чем больше в числе цифр, тем выше разряд самой первой цифры в этом числе.
К примеру, 123456>12345, потому что в первом числе цифра 1 обозначает сотню тысяч, а во втором – десяток тысяч.
Поэтому, для решения задач на сравнение чисел с разным количеством цифр, из которых они состоят, нам достаточно сравнить эти количества:
123456 – шестизначное число, 6 цифр;
12345 – пятизначное число, 5 цифр;
Например, сравним два числа: 12336 и 12345. Оба числа пятизначные. Значит, сравниваем каждую цифру, начиная с 5 разряда (десятков тысяч):
Сравнение двух, трех, и более чисел
Сравнивать между собой можно не только два натуральных числа.
Вернемся к примеру с конфетами на столе. Бабушка тоже купила конфеты и высыпала их на столе. Дети пересчитали их, и в бабушкиной кучке оказалось 33 штуки. Количество конфет мы можем записать натуральными числами: 25, 23 и 33.
Сравнив их между собой, мы увидим три неравенства:
Гораздо удобнее записать результат сравнения в виде двойного неравенства :
23
Как видите, все неравенства верны.
Чтобы быстро записать двойное, тройное, и т.д. неравенство, нужно расставить данные числа слева направо в порядке возрастания (предварительно сравнив между собой), оставив небольшие промежутки между ними. А после этого в оставленные промежутки записать знаки
Числовые и буквенные выражения
Числовые выражения
В этом разделе мы узнаем, что называют числовым выражением и значением выражения, научимся читать выражения.
Значение выражения — это результат выполненных действий.
Чтение числовых выражений
Решение числовых выражений
45 – (30 + 2) = …
Сначала выполняем действие, записанное в скобках. К 30 прибавляем 2.
30 + 2 = 32
Теперь нужно из 45 вычесть 38.
45 – 32 = 13
45 – (30 + 2) = 13
Сравнение значений числовых выражений
Сравнить числовое выражение – найти значение каждого из выражений и их сравнить.
Для этого найдем значения каждого из них:
Буквенные выражения
Буквенным называется математическое выражение, в котором используются цифры, знаки действий и буквы. Например, (47 + d) – 11.
Для записи буквенных выражений необходимо знать некоторые буквы латинского алфавита. Мы приводим его полностью, чтобы ты знал, с какими буквами можешь встретиться при составлении, решении или чтении буквенных выражений.
Чаще всего используются буквы:
a, b, c, d, x, y, k, m, n
Алгоритм решения буквенного выражения
1. Прочитать буквенное выражение
2. Записать буквенное выражение
3. Подставить значение неизвестного в выражении
4. Вычислить результат
Читаем выражение: Из 28 вычесть с или Найти разность числа 28 и с
Подставим вместо неизвестного «с» число 4.
У нас получается выражение: 28 – 4
Переменные
Буквы, которые содержатся в буквенных выражениях называются переменными. Например, в выражении с + x + 2 переменными являются буквы c и x. Если вместо этих переменных подставить любые числа, то буквенное выражение с + x + 2 обратится в числовое выражение, значение которого можно будет найти.
Числа, которые подставляют вместо переменных называют значениями переменных. Например, изменим значения переменных c и x. Для изменения значений используется знак равенства
Мы изменили значения переменных c и x. Переменной c присвоили значение 2, переменной x присвоили значение 3, тогда выражение с + х + 2 будет выглядеть так:
Теперь мы можем найти значение этого выражения:
с + х + 2 = 2 + 3 + 2 = 5 + 2 = 7
Поделись с друзьями в социальных сетях: