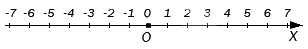Что значит сравнить с нулем
Сравнение числа с плавающей запятой с нулем
обновление
как отметил Даниил Daranas функции наверное, лучше назвать isNearlyEqual (что меня волнует).
кто-то указал этой ссылке, которым я хочу поделиться более заметно.
8 ответов
вы правы в своем наблюдении.
рекомендация FAQ В этом случае имеет ограниченная полезность. нет сравнения с плавающей запятой «один размер подходит всем». вам нужно подумать о семантике ваших переменных, допустимом диапазоне значений и величине ошибки, введенной вашими вычислениями. Даже в FAQ упоминается предостережение, говоря, что эта функция обычно не является проблемой,»когда значения x и y значительно больше, чем epsilon, но ваш пробег может отличаться».
функция, которую вы написали, не будет проверять два двойника на равенство, как обещает ее название. Он будет проверять только, если два двойника «достаточно близки» друг к другу.
Если вы действительно хотите проверить два двойника на равенство, используйте этот:
10.00000000000000001 не равно 10.0, независимо от того, что они вам говорят.
можно использовать std::nextafter фиксированный factor на epsilon стоимостью следующим образом:
2 + 2 = 5(*)
(для некоторых значений с плавающей точностью 2)
эта проблема часто возникает, когда мы думаем о»плавающей точке» как о способе повышения точности. Затем мы сталкиваемся с «плавающей» частью, что означает, что нет никакой гарантии номера могут быть представлены.
с текущими математическими операциями с плавающей запятой,не гарантируется, что (a / b) * b == A.
альтернативный подход заключается в том, чтобы полностью избежать проблемы, используя фиксированный точность точки или с помощью желаемой детализации в качестве базового блока для хранения. Е. Г. если вы хотите раз сохраняется с точностью до наносекунды, используйте наносекунд единицы хранения.
C++11 вводит std:: ratio в качестве основы для преобразования фиксированной точки между различными единицами времени.
if( FP_ZERO == fpclassify(x) ) do_something;
функция кажется совершенно допустимым для нулевого сравнения. Если вы планируете использовать его, я предлагаю вам использовать его везде, где есть поплавки, и не иметь особых случаев для таких вещей, как ноль, просто чтобы было единообразие в коде.
ps: Это аккуратная функция. Спасибо, что указал на него.
простое сравнение чисел FP имеет свою специфику, и его ключом является понимание формата FP (см. https://en.wikipedia.org/wiki/IEEE_floating_point)
когда числа FP вычисляются по-разному, один через sin(), другой, хотя exp (), строгое равенство не будет работать, даже если математически числа могут быть равными. Точно так же не будет работать равенство с константой. Фактически, во многих ситуациях номера FP не должны сравниваться с использованием строгое равенство (==)
Также см. пример, почему 10.0 == 10.0000000000000001
сравнение чисел с плавающей запятой dwo зависит от природы этих чисел, мы должны вычислить DBL_EPSILON для них, что было бы значимым для сравнения. Просто мы должны умножить DBL_EPSILON на одно из этих чисел. Кто из них? Максимум конечно
все другие способы дадут вам ошибки с неравенством, которые могут быть очень трудно поймать
Математика
Именная карта банка для детей
с крутым дизайном, +200 бонусов
Закажи свою собственную карту банка и получи бонусы
План урока:
В кабинет к шестиклассникам вошла Наталья Ивановна, и сообщила,что завтра в школе состоится выступление цирковой труппы, стоимость билета составляет 50 рублей. Желающие посетить представление, должны завтра принести деньги на приобретение билета. Ваня и Игнат очень хотели посмотреть выступление, договорились приобрести билеты. Однако, Игнат забыл деньги дома. Мальчик очень огорчился. Наталья Ивановна заметила грустного ученика и предложила купить билет вместо него, с условием, что мальчик принесет забытую купюру завтра. Друзья с радостью пошли на представление.
Сравнение положительных чисел с нолем
Чтобы не испытывать трудностей при выполнении сравнения положительных чисел и нуля, давайте рассмотрим задачу.
У Марины в кармане было четыре конфеты, а в Наташином кармашке лежало 0 конфет. Подумайте и объясните, у кого из девочек имелось большее количество конфет.
Изучив условие задачи, мы понимаем, что для ответа на главный вопрос задачи нужно выполнить сравнение количества Марининых сладостей с количеством сладостей, имеющихся у Натальи, то есть 4 и 0.
Давайте определим, к каким числам можно отнести значение четыре? К положительным или отрицательным?
Вспомним определение положительного:
Положительными числами называют числа со знаком +.На письме, не принято ставить знак «плюс» перед положительными числами. Считается, что если перед числом не стоит знак «минус», то число является положительным.
Исходя из определения, рассматриваемое значение считается положительным.
Переходим ко второму числу: 0.
Обязательно нужно понимать, что такое 0.
0 является целым числом, но при этом, не обозначает количество предметов.
Если будем рассматривать ноль в обычной жизни, то можно сказать иначе: 0 = «ничего».
в кассе 0 рублей = касса пуста, денег нет;
улов дедушки составил 0 рыб = дедушка ничего не поймал;
мальчик вынес во двор 0 игрушек = мальчик не вынес во двор игрушки.
Делаем вывод, что у Наташи не было конфет, а у Марины было 4 леденца.
Теперь можно выполнить сравнение положительного числа 4 с числом 0.
Даже ребенок понимает, что четыре конфетки больше, чем ничего или 0.
Из рассмотренного пояснения следует:
любое положительное число всегда будет больше, чем ноль!
Сравнение отрицательных чисел с нулем
Теперь, давайте разберемся, как сравнить отрицательное число с нулем. Для начала вспомним, какие числа называют отрицательными.
Чтобы разобрать данную ситуацию, нужно определить, в какой из дней на улице будет теплее, следовательно, температура воздуха будет выше (больше). Для этого необходимо сравнить прогнозируемую температуру четверга и пятницы. По условию, в четверг 0˚C, а в пятницу-2˚C. Получается, что нам нужно сравнить отрицательное число и ноль. А как это правильно сделать? В математике существует правило, которое говорит:
Ноль всегда будет больше любого отрицательного числа.
Исходя из рассмотренного правила, сравним предполагаемые показатели термометра в указанные дни:
0>-2 – ноль больше, чем минус два.
Теперь, мы можем сказать, что в четверг температура воздуха будет больше (выше), а значит, именно в этот день будет теплее.
Выполнять сравнение цифровых записей со знаком «минус» и ноля очень просто, главное помнить, что ноль всегда больше любого отрицательного числа!
Сравнение положительных и отрицательных чисел
Как выполнять сравнение положительных и отрицательных чисел с нолем мы уже знаем, а как же сравнивать числа со знаками «плюс» и «минус» между собой? Математика предусмотрела и этот вариант сравнения чисел. Существует правило сравнения положительных и отрицательных чисел.
При сравнении положительного и отрицательного числа, большим всегда будет положительное число.
Рассмотрим на примере.
Сравнение отрицательных чисел
Теперь давайте рассмотрим, как правильно сравнивать числовые значения со знаком «минус».
Если возникла необходимость сравнить отрицательные числа, то нужно помнить простое правило сравнения отрицательных чисел.
Из двух отрицательных чисел большим будет то число, модуль которого меньше.
Разберем на примере.
Вначале, кажется, что сравнивать такие числа очень просто и с этим заданием справится даже первоклассник. Но на самом деле, для выполнения сравнения данных значений необходимо соблюдать следующий алгоритм:
Модуль любого числа всегда имеет только положительное значение.
Для положительного числа модуль равен этому числу:
3=|3|, 24=|24|.
Так как перед каждой записью стоит знак минус, то числа считаются отрицательными, а модуль отрицательного числа равен противоположному числовому значению самого числа.
Рассмотренное правило, говорит о том, что большим будет то число, которое имеет меньший модуль.
При выполнении сравнения значений со знаком минус важно помнить, большим будет то число, модуль которого меньше!
Сравнение числовых значений с использованием горизонтальной координатной прямой
Ну а теперь, рассмотрим еще одни способ сравнения цифровых записей с разными знаками.
Давайте начертим координатную прямую. Для этого, вспомним, что представляет собой координатная прямая.
Координатная прямая – прямая линия, имеющая направление, точку начала отсчета и единичный отрезок.
Отметим на прямой точки A(-4), C(-2), B(2),D(3).
Помни!Точки с положительным значением координаты расположены справа от точки начала отсчета, точки с отрицательным значением координаты находятся слева от точки начала отсчета.
И теперь, с помощью горизонтальной координатной прямой давайте рассмотрим математическое действие – сравнение чисел.
Мы знаем, что точки с положительными координатами, расположились справа от точки начала отсчета, а с отрицательными слева. На координатную прямую нанесены точки B и D, имеющие координаты со знаком «плюс». Сравним координаты данных точек.
Используя рассмотренное правило, делаем вывод, что точка с любой положительной координатой, находится на координатной прямой, правее точки начала отсчета, а значит, имеет большее числовое значение.
То есть, ноль всегда меньше любого положительного числа.
Любая точка, имеющая отрицательное значение координаты, всегда будет расположена левее точки 0, следовательно, любая числовая запись со знаком «минус» всегда меньше 0.
Сравнивать очень просто и интересно, главное запомнить простые правила сравнения и верно использовать их при выполнении заданий!
JavaScript: загадочное дело выражения null >= 0
Однажды я собирал материалы чтобы устроить ликбез по JavaScript для пары коллег. Тогда я и наткнулся на довольно интересный пример, в котором рассматривалось сравнение значения null с нулём. Собственно говоря, вот этот пример:
На первый взгляд — полная бессмыслица. Как некое значение может быть не больше, чем 0, не равно нулю, но при этом быть больше или равно нулю?
Хотя поначалу я оставил это без особого внимания, решив, что всё дело в том, что JavaScript — это JavaScript, со всеми его странностями, этот пример меня заинтриговал. Связано ли это с типом null и с тем, как он обрабатывается, или с тем, как выполняются операции сравнения значений?
В итоге я решил докопаться до сути происходящего и начал рыться в единственном источнике истины для JavaScript — в спецификации ECMA. Сегодня я хочу рассказать вам о том, в какую глубокую кроличью нору я в результате провалился.
Абстрактный алгоритм сравнения для отношений
Рассмотрим первое сравнение:
Шаги 1 и 2 предлагают нам вызвать оператор ToPrimitive() для значений null и 0 для того, чтобы привести эти значения к их элементарному типу (к такому, например, как Number или String ). Вот как ToPrimitive преобразует различные значения:
| Входной тип | Результат |
| Undefined | Преобразование не производится |
| Null | Преобразование не производится |
| Boolean | Преобразование не производится |
| Number | Преобразование не производится |
| String | Преобразование не производится |
| Object | Возвращает значение по умолчанию для объекта. Значение по умолчанию для объекта получается путём вызова для объекта внутреннего метода [[DefaultValue]] с передачей ему опциональной подсказки ПредпочтительныйТип. |
| Входной тип | Результат |
| Undefined | NaN |
| Null | +0 |
| Boolean | Результат равен 1, если аргумент равен true. Результат равен +0, если аргумент равен false. |
| Number | Преобразование не производится |
| … | … |
Итак, почему null не больше и не меньше нуля мы выяснили. Теперь идём дальше — разберёмся с тем, почему null ещё и не равен нулю.
Абстрактный алгоритм сравнения для равенств
Рассмотрим теперь проверку на равенство null и 0 :
Теперь, когда ещё одна «тайна» JavaScript» раскрыта, разберёмся с оператором «больше или равно».
Оператор больше или равно (>=)
Выясним теперь, почему истинно такое выражение:
Тут спецификация полностью выбила меня из колеи. Вот как, на очень высоком уровне, работает оператор >=:
В результате мы и получаем:
Итоги
Уважаемые читатели! Знаете ли вы о каких-нибудь странностях JavaScript, которые, после чтения документации, уже перестают казаться таковыми?
Сравнение целых чисел: правила, примеры
После того, как получили полное представление о целых числах, можно говорить об их сравнении. Для этого выясняется, какие числа равные и неравные. Разберутся правила, благодаря которым выясняем, какие из двух неравных больше или меньше. Это правило основано на сравнении натуральных чисел. Будет рассмотрено сравнение трех и более целых чисел, нахождение наименьшего и наибольшего целого числа из заданного множества.
Равные и неравные целые числа
Сравнение двух чисел приводит к тому, что они либо равны либо не равны. Рассмотрим определения.
Два целых числа называют равными, когда их запись полностью совпадает. Иначе они считаются неравными.
При сравнивании чисел используется правило модуля числа.
Если два числа имеют одинаковые знаки и их модули равны, то эти два числа считаются равными. Иначе их называют не равными.
Рассмотрим на примере данное определение.
Видно, что числа имеют одинаковый знак, но это не значит, что они равны. Для сравнения используется модуль числа. По модулю первое число оказалось меньше второго. Они не равны ни по модулю, ни без него.
Значит, делаем вывод, что числа не равны.
Рассмотрим еще пример.
Если получаем неравные числа, тогда необходимо уточнение, какое из них меньше и какое больше.
Сравнение произвольных целых чисел с нулем
При сравнении отрицательных чисел с нулем другая ситуация. Все числа, которые меньше нуля, считаются отрицательными. Отсюда делаем вывод, что любое отрицательное число меньше нуля, нуль равен нулю, а любое целое положительное больше нуля. Суть правила заключается в том, что нуль больше отрицательных чисел, но меньше всех положительных.
Сравнение положительных целых чисел
Все целые положительные числа являются натуральными. Значит, равнение положительных чисел аналогично сравнению натуральных.
Рассмотрим еще один пример.
Сравнение целых отрицательных и положительных чисел
Любое целое отрицательное число меньше целого положительного и наоборот.
Сравним несколько чисел и рассмотрим на примере.
Сравнение целых отрицательных чисел
Рассмотрим правило сравнения:
Из двух отрицательных чисел меньшим является то, модуль которого больше и наоборот.
Рассмотрим на примере.
Сравниваемые целые числа на координатной прямой
Рассмотрим целые числа, расположенные на координатной прямой.
Из рассмотренных выше правил получим, что на горизонтальной координатной прямой точки, которым соответствуют большие целые числа, то есть лежат правее тех, которым соответствуют меньшие.
Начало отсчета – это ноль. Он больше всех отрицательных и меньше всех положительных. Также и с точками, находящимися на координатной прямой.
Наибольшее отрицательное и наименьшее положительное целое число
В предыдущих пунктах подробно было рассмотрено сравнение двух целых чисел. В данном пункте поговорим о сравнении трех и более чисел, рассмотрим ситуации.
Когда производится сравнение нескольких чисел, то появляется определение наибольшего и наименьшего значения числа.
Число заданного множества считается наименьшим, если оно меньше любого другого из заданных чисел множества.
Число заданного множества является наибольшим, если оно больше любого другого из заданных чисел множества.
Очевидно, что множество целых чисел огромно и бесконечно, поэтому указать наименьшее или наибольшее число невозможно. Это можно сделать только в заданном множестве чисел. Число, расположенное правее на координатной прямой, всегда считается большим, чем то, которое левее.
Вариант 1. С-20. № 6. ГДЗ Алгебра 7 класс Звавич. Сравните с нулем значение выражения. Поможете?
Say you are fond of both things.
Example: I am fond of both fruit and vegetables. ( Подробнее. )
Завод по плану должен был изготовить 537 000 изделий. План был выполнен на 102,5%. Установите:
1) сколько изделий выпустил ( Подробнее. )
Упростите выражение:
1) а) 2,8 ∙ 5а; б)-3,5а ∙ 4; в) 3,6 ∙ 0,8а; г)-8а ∙ (-12);
2) а) ( Подробнее. )
Решите задачу:
За 3 ч мотоциклист проезжает то же расстояние, что велосипедист за 5 ч. Скорость мотоциклиста на 12 км/ч больше ( Подробнее. )