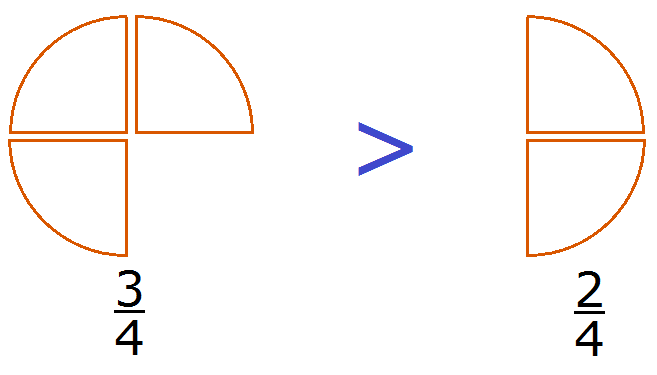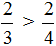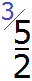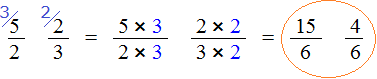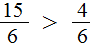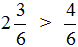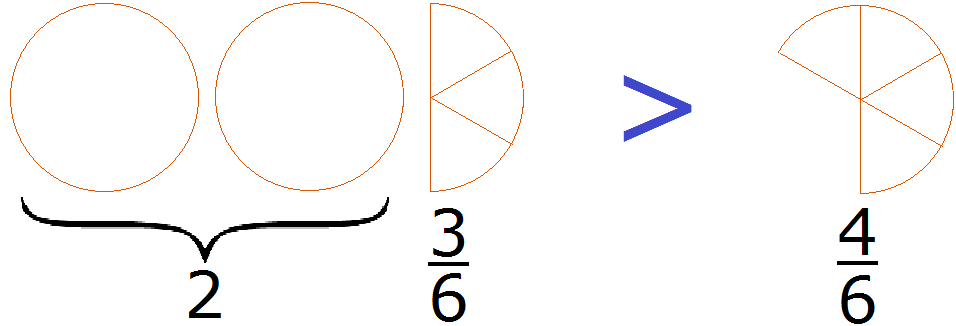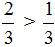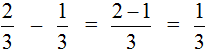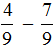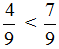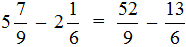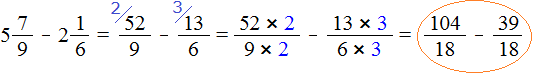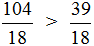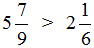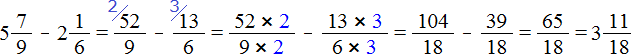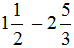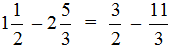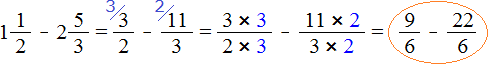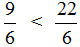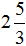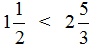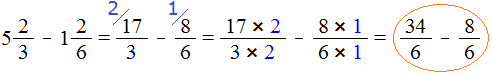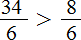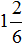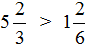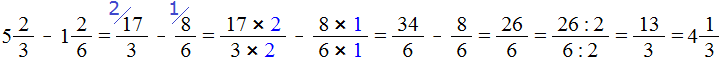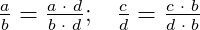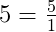Что значит сравнить дроби 6 класс

Сравнение дробей: правила, примеры, решения

Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.

Сравнение дробей с одинаковыми знаменателями

Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.

Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.

Сравнение дробей с разными знаменателями

Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.

Если имеются дроби с разными знаменателями, для их сравнения необходимо:

Рассмотрим данные действия на примере.

Ответ: 5 18 > 23 86 .

Сравнение дробей с одинаковыми числителями

Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.

Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.

Рассмотрим на примере.

Решение

Сравнение дроби с натуральным числом

Источник

Сравнение дробей

Продолжаем изучать дроби. Сегодня мы поговорим об их сравнении. Тема интересная и полезная. Она позволит новичку почувствовать себя учёным в белом халате.

Суть сравнения дробей заключается в том, чтобы узнать какая из двух дробей больше или меньше.

Чтобы ответить на вопрос какая из двух дробей больше или меньше, пользуются операциями отношения, такими как больше (>) или меньше ( )

Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с одинаковыми числителями

Следующий случай это когда числители дробей одинаковые, но знаменатели разные. Для таких случаев предусмотрено следующее правило:

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше. И соответственно меньше та дробь, у которой знаменатель больше.

Например, сравним дроби и . У этих дробей одинаковые числители. У дроби знаменатель меньше, чем у дроби . Значит дробь больше, чем дробь . Так и отвечаем:

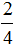
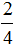
Этот пример можно легко понять, если вспомнить про пиццы, которые разделены на три и четыре части. пиццы больше, чем пиццы:

Каждый согласится с тем, что первая пицца больше, чем вторая.

Сравнение дробей с разными числителями и разными знаменателями

Чтобы ответить на вопрос, какая из этих дробей больше или меньше, нужно привести их к одинаковому (общему) знаменателю. Затем можно будет легко определить какая дробь больше или меньше.

Приведём дроби и к одинаковому (общему) знаменателю. Найдём наименьшее общее кратное (НОК) знаменателей обеих дробей. НОК знаменателей дробей и это число 6.

Теперь находим дополнительные множители для каждой дроби. Разделим НОК на знаменатель первой дроби . НОК это число 6, а знаменатель первой дроби это число 2. Делим 6 на 2, получаем дополнительный множитель 3. Записываем его над первой дробью:

Умножим дроби на свои дополнительные множители:

Мы пришли к тому что дроби, у которых были разные знаменатели, превратились в дроби, у которых одинаковые знаменатели. А как сравнивать такие дроби мы уже знаем. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше:

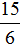
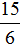
Правило правилом, а мы попробуем разобраться почему больше, чем . Для этого выделим целую часть в неправильной дроби . В дроби ничего выделять не нужно, поскольку эта дробь уже правильная.

После выделения целой части в дроби 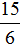, получим следующее выражение:

Теперь можно легко понять, почему 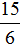больше, чем . Давайте нарисуем эти дроби в виде пицц:

2 целые пиццы и пиццы, больше чем пиццы.

Вычитание смешанных чисел. Сложные случаи.

Вычитая смешанные числа иногда можно обнаружить, что всё идёт не так гладко как хотелось бы.

При вычитании чисел уменьшаемое должно быть больше вычитаемого. Только в этом случае будет получен нормальный ответ.

Уменьшаемое 10 больше вычитаемого 8, поэтому мы получили нормальный ответ 2.

А теперь посмотрим, что будет если уменьшаемое окажется меньше вычитаемого. Пример 5 − 7 = −2

В этом случае мы выходим за пределы привычных для нас чисел и попадаем в мир отрицательных чисел, где нам ходить пока рано, а то и опасно. Чтобы работать с отрицательными числами, нужна соответствующая математическая подготовка, которую мы ещё не получили.

Если при решении примеров на вычитание вы обнаружите, что уменьшаемое меньше вычитаемого, то можете пока пропустить такой пример. Работать с отрицательными числами допустимо только после их изучения.

С дробями ситуация та же самая. Уменьшаемое должно быть больше вычитаемого. Только в этом случае можно будет получить нормальный ответ. А чтобы понять больше ли уменьшаемая дробь, чем вычитаемая, нужно уметь сравнить эти дроби.

Например, решим пример .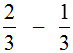

Это пример на вычитание. Чтобы решить его, нужно проверить больше ли уменьшаемая дробь, чем вычитаемая. больше чем

поэтому смело можем вернуться к примеру и решить его:

Теперь решим такой пример

Проверяем больше ли уменьшаемая дробь, чем вычитаемая. Обнаруживаем, что она меньше:

В этом случае разумнее остановиться и не продолжать дальнейшее вычисление. Вернёмся к этому примеру, когда изучим отрицательные числа.

Смешанные числа перед вычитанием тоже желательно проверять. Например, найдём значение выражения .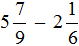

Сначала проверим больше ли уменьшаемое смешанное число, чем вычитаемое. Для этого переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Чтобы сравнить такие дроби, нужно привести их к одинаковому (общему) знаменателю. Не будем подробно расписывать как это сделать. Если испытываете затруднения на этом моменте, обязательно изучите действия с дробями.

После приведения дробей к одинаковому знаменателю, получаем следующее выражение:

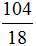
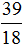
Теперь нужно сравнить дроби и . Это дроби с одинаковыми знаменателями. Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

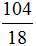
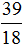
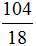
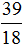
У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит что уменьшаемое 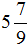больше, чем вычитаемое

А значит мы можем вернуться к нашему примеру и смело решить его:

Пример 3. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем данные дроби к одинаковому (общему) знаменателю:

Теперь сравним дроби и . У дроби числитель меньше, чем у дроби , значит дробь меньше, чем дробь

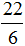
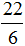
А это значит, что и уменьшаемое 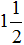меньше, чем вычитаемое

А это гарантировано приведёт нас в мир отрицательных чисел. Поэтому разумнее остановиться на этом месте и не продолжать вычисление. Продолжим его после изучения отрицательных чисел.

Пример 4. Найти значение выражения

Проверим больше ли уменьшаемое, чем вычитаемое.

Переведём смешанные числа в неправильные дроби:

Получили дроби с разными числителями и разными знаменателями. Приведем их к одинаковому (общему) знаменателю:

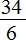
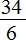
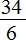
Теперь нужно сравнить дроби и . У дроби числитель больше, чем у дроби . Значит дробь больше, чем дробь .

А это значит, что уменьшаемое 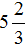больше, чем вычитаемое

Поэтому мы смело можем продолжить вычисление нашего примера:

Сначала мы получили ответ . Эту дробь мы сократили на 2 и получили дробь , но такой ответ нас тоже не устроил и мы выделили целую часть в этом ответе. В итоге получили ответ .

Источник

Сравнение дробей. Как сравнивать дроби с разными знаменателями?

Не только простые числа можно сравнивать, но и дроби тоже. Ведь дробь — это такое же число как, к примеру, и натуральные числа. Нужно знать только правила, по которым сравнивают дроби.

Сравнение дробей с одинаковыми знаменателями.

Если у двух дробей одинаковые знаменатели, то такие дроби сравнить просто.

Чтобы сравнить дроби с одинаковыми знаменателями, нужно сравнить их числители. Та дробь больше у которой больше числитель.

Знаменатели у обоих дробей одинаковые равны 26, поэтому сравниваем числители. Число 13 больше 7. Получаем:

Если мы до решаем эти дроби, то получим числа \(\frac<20> <4>= 5\) и \(\frac<20> <10>= 2\). Получаем, что 5 > 2

В этом и заключается правило сравнения дробей с одинаковыми числителями.

Рассмотрим еще пример.

Так как числители одинаковые, больше та дробь, где знаменатель меньше.

Пример №2:
Сравните правильную дробь с единицей?

Решение:
Любая правильная дробь всегда меньше 1.

Задача №1:
Сын с отцом играли в футбол. Сын из 10 подходов в ворота попал 5 раз. А папа из 5 подходов попал в ворота 3 раза. Чей результат лучше?

Решение:
Сын попал из 10 возможных подходов 5 раз. Запишем в виде дроби \(\frac<5> <10>\).
Папа попал из 5 возможных подходов 3 раз. Запишем в виде дроби \(\frac<3> <5>\).

Сравним дроби. У нас разные числители и знаменатели, приведем к одному знаменателю. Общий знаменатель будет равен 10.

Источник

Сравнение обыкновенных дробей

Сравнить две дроби — значит определить, какая из дробей больше, какая меньше или установить, что дроби равны.

Сравнение дробей с одинаковыми знаменателями

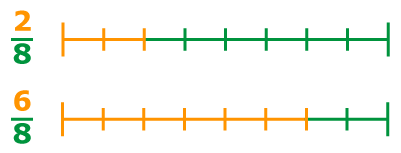
Из двух дробей с одинаковыми знаменателями больше та дробь, у которой числитель больше.

Пример. Дробь 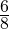больше чем дробь , потому что доли в обеих дробях одинаковы, но в первой дроби их больше, чем во второй.

Если изобразим единицу отрезком и разделим его на 8 долей, то легко увидеть, что дробь 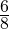больше :

Сравнение дробей с одинаковыми числителями

Из двух дробей с одинаковыми числителями больше та дробь, у которой знаменатель меньше.

Пример. Дробь 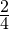больше чем дробь , потому что число долей в обеих дробях одинаково, но в первой дроби доли крупнее, чем во второй.

Изобразим две единицы в виде кругов, один разделим на 4 доли, второй на 6 долей. Теперь можно увидеть, что дробь 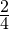больше :

Сравнение дробей с разными знаменателями и числителями

Чтобы сравнить дроби, у которых разные числители и знаменатели, нужно привести их к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дроби: и .

Решение: приводим данные дроби к общему знаменателю:

Теперь сравниваем их по правилу сравнения дробей, у которых одинаковые знаменатели. Так как 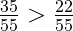, значит .

Приведём ещё один способ сравнения дробей с разными знаменателями и числителями. Рассмотрим сначала числовой пример.

Пример. Сравним дроби и .

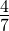
Решение: приводим данные дроби к общему знаменателю:

Решая данный пример можно заметить, что, после приведения дробей к общему знаменателю, задача сравнения свелась фактически к сравнению произведений

Так как 2 · 7 = 14, а 4 · 3 = 12, то

Значит, .

Теперь решим эту же задачу в общем виде, используя буквенную запись.

Пример. Пусть даны дроби и , где a и c — нуль или натуральные числа, b и d — натуральные числа. Приведём дроби к общему знаменателю:

Сравнение неправильной дроби с натуральным числом сводится к сравнению двух дробей.

Чтобы сравнить неправильную дробь с натуральным числом, нужно натуральное число представить в виде неправильной дроби со знаменателем 1, затем их можно сравнить одним из двух способов: используя перекрёстное правило, либо привести дроби к общему знаменателю. После этого их сравнивают по правилу сравнения дробей, у которых одинаковые знаменатели.

Пример. Сравните дробь с числом 5.

Решение: представим число 5 в виде дроби со знаменателем 1:

Приводим дроби к общему знаменателю:

Сравниваем числители, так как 11 Пример.

Онлайн калькулятор сравнения дробей

Источник