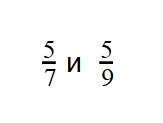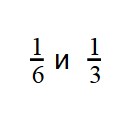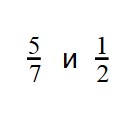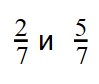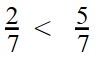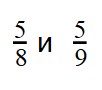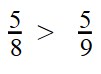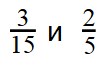Что значит сравнение вычисляя
Сравнение натуральных чисел
Сравнить два числа — это значит определить, равны они или нет, если нет, то определить, какое из них больше, а какое — меньше.
Равные и неравные натуральные числа
Если записи двух натуральных чисел одинаковы, то говорят, что эти числа равны между собой. Числа, которые равны, называются равными. Если записи двух натуральных чисел отличаются, то говорят, что эти числа не равны. Числа, которые не равны, называются неравными.
Пример. Натуральное число 34 равно числу 34 (их записи одинаковы), а натуральные числа 63 и 67 не равны (их записи различны). Следовательно числа 34 и 34 — равные, а 63 и 67 — неравные.
Равенства и неравенства
Для записи результата сравнения чисел используются следующие знаки:
Запись, которая состоит из математических выражений, между которыми ставится знак = называется равенством.
2 + 3 = 5 — равенство.
2 + 2 = 1 + 1 + 2 — равенство (подобные записи представляют собой равенство двух числовых выражений, и означают равенство значений этих выражений).
Равенства могут быть как верными (например, 5 = 5 — верное равенство), так и неверными (например, 11 = 14 — неверное равенство).
Знаки > и должны быть обращены остриём к меньшему числу.
Запись, которая состоит из математических выражений, между которыми ставится знак > или называется неравенством.
2 8 — неверное неравенство).
Правила чтения равенств и неравенств
Равенства и неравенства читаются слева направо. Левая часть равенства читается в именительном падеже, а правая — в дательном.
Пример. 7 = 7 — семь равно семи.
Левая часть неравенства читается в именительном падеже, а правая — в родительном.
Пример. 11 > 9 — одиннадцать больше девяти, 3 Пример. Сравним числа 1 и 3, 7 и 4. Запишем все однозначные натуральные числа в одной строке в следующем порядке:
Число 1 меньше числа 3 (1 4), так как в натуральном ряду число 7 находится правее числа 4.
Для применения правил сравнения чисел по их десятичной записи необходимо принять одну условность: будем считать, что число 0 меньше любого натурального числа, и что нуль равен нулю.
Правила сравнения натуральных чисел по их десятичной записи:
Если записи сравниваемых чисел состоят из одинакового количества цифр, то числа сравниваются поразрядно слева направо. Большим будет считаться то число, у которого первая (слева направо) из неодинаковых цифр больше.
Когда говорят, что цифры равны (или одна цифра больше другой), то имеют ввиду, что соответствующие им числа равны (или одно число больше другого).
Пример. Сравним натуральные числа 4026 и 4019. Для удобства сравнения можно записать их одно под другим:
Сначала сравниваем значения разряда тысяч. Получаем равенство 4 = 4, поэтому переходим к сравнению значений следующего разряда. Опять получаем равенство 0 = 0, переходим к сравнению значений разряда десятков. Теперь имеем неравенство 2 > 1, из которого делаем вывод, что число 4026 больше числа 4019 (4026 > 4019), потому что у первого числа, цифра разряда десятков (2) больше, чем цифра разряда десятков (1) у второго числа.
Если количество цифр в записи сравниваемых чисел разное, то большим будет считаться то число, у которого количество цифр больше.
Пример. Сравним натуральные числа 347 503 и 34 503. Для удобства сравнения можно записать их одно под другим:
Записав числа одно под другим, можно наглядно заметить, что первое число имеет большее количество цифр, чем второе, следовательно 347 503 > 34 503.
Два натуральных числа равны, если у них одинаковое количество цифр и цифры одинаковых разрядов равны.
Пример. Сравним числа 38 526 734 и 38 526 734. Для удобства сравнения можно записать их одно под другим:
38 526 734
38 526 734
Записи данных чисел одинаковы (количество цифр и цифры одинаковых разрядов равны), следовательно эти числа равны.
Двойные неравенства, тройные неравенства и т. д.
Когда нужно записать, что одно число больше другого, но меньше третьего, часто используют двойные неравенства.
В виде двойного неравенства можно записывать результат сравнения трёх натуральных чисел.
Пример. Допустим, нужно сравнить три натуральных числа 11, 34 и 8. Сравнивая данные числа между собой, получим три неравенства 11 8, которые можно записать как двойное неравенство:
Сравнение натуральных чисел
Вам уже известно, что натуральные числа используются для обозначения количества тех или иных предметов. Возьмем, к примеру, конфеты. Мама купила шоколадные батончики и высыпала их кучкой на столе. Дети пересчитали, и их оказалось 25 штук.
Пришел с работы папа и высыпает рядом еще конфеты. На первый взгляд, эта кучка не отличается от первой, но пересчитав количество папиных конфет, дети увидели, что их всего 23. Значит, эти кучки разные. Чтобы это выяснить, дети произвели два действия:
Сравнить натуральные числа – это означает узнать, отличаются ли они друг от друга или они одинаковые. Если сравниваемые числа отличаются, тогда мы может узнать, что одно число больше другого, а второе, соответственно, меньше первого.
Как сравнить натуральные числа
Сравнить натуральные числа можно такими способами:
В результате сравнения мы можем получить:
Равенство натуральных чисел
Если два натуральных числа имеют полностью одинаковую запись, то и записанные с их помощью числа одинаковы (говорят просто – они равны). Если их записи отличаются, тогда эти числа не равны.
Если мы определили, что числа не равны, тогда нам необходимо выяснить, какое положение они занимают по отношению друг к другу, большее или меньшее.
Запись и чтение неравенств
Неравенство – это запись чисел или математических выражений, которая содержит знаки неравенства.
Читается подобная запись следующим образом. Первое число называется в именительном падеже (кто? что?), а второе в родительном (кого? чего?). Например, так: «два меньше четырех», «восемьдесят девять больше семидесяти восьми».
Если стрелка смотрит влево: « меньше » и означает, что слева от него находится число меньшее, чем справа.
Если стрелка смотрит вправо: «>», такой знак называется « больше » и означает, что слева от него находится большее число, чем справа.
Стрелка знака всегда указывает на меньшее число, а двойная вилка – на большее!
Например, дано неравенство 5 верным (правильно отмеченным), например, 1 неверным (неправильно отмеченным), например, 5>6.
Сравнение однозначных натуральных чисел с помощью ряда
Этот способ лучше всего подходит для сравнения однозначных натуральных чисел.
Меньшим называют число, которое в натуральном ряду находится раньше другого, а большим – то, которое расположено позже другого.
Например, число 2 в натуральном ряду стоит раньше, чем число 4, значит, 2 8.
Число 1 (единица) – самое меньшее из натуральных чисел, поскольку стоит в натуральном ряду первым.
На координатном луче меньшее число обозначается раньше (левее), а большее число – позже (правее) другого числа.
Рис. 1. Большее и меньшее число на координатном луче.
Действительно, чем больше в числе цифр, тем выше разряд самой первой цифры в этом числе.
К примеру, 123456>12345, потому что в первом числе цифра 1 обозначает сотню тысяч, а во втором – десяток тысяч.
Поэтому, для решения задач на сравнение чисел с разным количеством цифр, из которых они состоят, нам достаточно сравнить эти количества:
123456 – шестизначное число, 6 цифр;
12345 – пятизначное число, 5 цифр;
Например, сравним два числа: 12336 и 12345. Оба числа пятизначные. Значит, сравниваем каждую цифру, начиная с 5 разряда (десятков тысяч):
Сравнение двух, трех, и более чисел
Сравнивать между собой можно не только два натуральных числа.
Вернемся к примеру с конфетами на столе. Бабушка тоже купила конфеты и высыпала их на столе. Дети пересчитали их, и в бабушкиной кучке оказалось 33 штуки. Количество конфет мы можем записать натуральными числами: 25, 23 и 33.
Сравнив их между собой, мы увидим три неравенства:
Гораздо удобнее записать результат сравнения в виде двойного неравенства :
23
Как видите, все неравенства верны.
Чтобы быстро записать двойное, тройное, и т.д. неравенство, нужно расставить данные числа слева направо в порядке возрастания (предварительно сравнив между собой), оставив небольшие промежутки между ними. А после этого в оставленные промежутки записать знаки
Сравнение дробей: как правильно
Сравнение дробей с одинаковыми знаменателями
Как и при любом другом сравнении, суть сравнения дробей — в том, чтобы определить меньшую и большую дроби.
Нет ситуации более благоприятной для сравнения, чем дроби с одинаковыми знаменателями. Если вся разница между дробями только в числителях, пользуемся следующим правилом:
Из двух дробей с одинаковыми знаменателями больше дробь с большим числителем. А меньше будет та дробь, числитель которой меньше.
А теперь на примерах.
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Как видите, нет ничего сложного в сравнении дробей, если знаменатели равны. Вся задача заключается в том, чтобы определить больший и меньший числитель.
Давайте разберем наглядный пример сравнения дробей. Еще больше наглядных примеров — на курсах по математике в онлайн-школе Skysmart!
Допустим, в торте 6 кусков. Если от целого торта отрезать один кусок — в торте останется 5 кусков.
Понять, что целый торт больше, чем торт без одного куска, можно и без сравнения дробей. Но это же самое правило можно применить и при менее очевидных сравнениях, которые часто встречаются в повседневной жизни.
Сравнение дробей с одинаковыми числителями
Вы уже разобрались со сравнением дробей с одинаковыми знаменателями. Теперь задача чуть усложняется — научимся сравнивать дроби с разными знаменателями, но с одинаковыми числителями.
Если у двух дробей одинаковые числители, то больше будет та дробь, чей знаменатель меньше. А меньше будет дробь с большим знаменателем.
А теперь наши любимые примеры. Погнали!
Пример 1. Сравните дроби:
Пример 3. Сравните дроби:
Сравнение дробей с разными числителями и разными знаменателями
Нет ничего хитрого в сравнении дробей с одинаковыми числителями или знаменателями. Чуть больше усилий потребуется при сравнении дробей, в которых нет ничего одинакового.
Сначала вспомним, как привести дроби к общему знаменателю.
Рассмотрим пример дробей с разными знаменателями.
Давайте потренируемся в сравнении дробей.
Пример 1. Сравните дроби:
При сравнении неправильных дробей с правильными помните, что неправильная дробь всегда больше правильной.
Пример 2: Сравните дроби:
Вычитание смешанных чисел
Вычитание проходит гладко, когда уменьшаемое больше вычитаемого.
В случае, если вычитаемое больше уменьшаемого, разность оказывается отрицательной. В этом нет ничего страшного. Но математика в 5 классе — «положительная», поэтому научимся находить разность смешанных чисел, не скатываясь «в минусы».
При вычитании дробей действует тот же самый принцип: вычитаемое должно быть меньше уменьшаемого. Вот здесь то вам и пригодится навык сравнивать дроби.
Пример 1. Вычислите:
Вычитаемая дробь меньше уменьшаемой
Пример 2.Найдите разность:
Примеры для самопроверки
Теория — это, конечно, хорошо. Но без практики — никуда. Пора потренироваться в решении примеров и закрепить тему сравнения дробей.
Пример 1. Сравните дроби:
Ответ: по правилу сравнения дробей с одинаковыми знаменателями, больше та дробь, у которой числитель больше. Это значит, что
Пример 2. Сравните дроби:
Ответ: по правилу сравнения дробей с разными знаменателями и одинаковыми числителями, больше та дробь, чей знаменатель меньше. Это значит, что
Пример 3. Сравните дроби:
Ответ: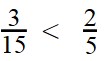
Урок 30 Бесплатно Сравнение чисел
В этом уроке мы научимся сравнивать числа как с разными, так и c одинаковыми знаками.
Узнаем, что такое быстрое сравнение с нулем, а также поговорим про то, что касается сравнения чисел и модулей.
Сравнение чисел с одинаковым знаком
Со сравнением двух чисел, оба из которых больше нуля, вы уже знакомы: для этого мы просто смотрим на числа, их разряды и понимаем, какое из них больше. Для нас очевидно еще с начальной школы, что 3 больше, чем 2, 154 больше, чем 145, 1428 больш,е чем 425, и так далее.
Если говорить про отрицательные числа, то для начала приведем аналогию из реальной жизни.
То есть, казалось бы, 10 больше, чем 7, но при этом -10°С меньше, чем -7°С.
Чтобы сравнить два числа, оба из которых отрицательные, надо сравнить их модули, тогда меньше будет то число, у которого модуль больше.
Это же работает и в обратную сторону.
Если два числа отрицательны и модуль первого меньше модуля второго, то первое число больше второго.
Если оба числа отрицательны и их модули равны, то и сами числа равны.
Пример:
Допустим, необходимо сравнить \(\mathbf<-324>\) и \(\mathbf<-245>\)
Первым делом находим модули:
Также сравним \(\mathbf<-5>\) и \(\mathbf<-5>\)
Мы видим, что модули чисел равны, к тому же, они оба отрицательны, значит эти числа равны.
Пройти тест и получить оценку можно после входа или регистрации
Сравнение чисел с разными знаками
Сейчас мы познакомимся с одним интересным свойством сравнения, которое позволит нам сравнивать числа с разными знаками вообще без каких-либо усилий с нашей стороны.
Задумывались ли вы раньше, почему если мы знаем, что Борис выше Анны, а Сергей выше Бориса, мы сразу сделаем вывод, что Сергей выше и Анны тоже?
Или если мы знаем, что Ваня пришел раньше Пети, а Петя раньше Ильи, то мы делаем вывод, что Ваня пришел раньше Ильи.
Это свойство называется транзитивностью.
Если говорить абстрактно, то это свойство говорит о следующем: если между объектом А и объектом Б есть транзитивное отношение и между объектом Б и объектом В тоже есть это же транзитивное отношение, то это значит, что это отношение есть между А и В.
Звучит может немного непонятно, но на примере со сравнением сейчас все встанет на свои места.
Отношения «быть больше», «быть равным» и «быть меньше» обладают свойством транзитивности.
Поэтому если мы знаем, что 2 меньше, чем 3, а 3 меньше, чем 4, то мы можем утверждать, что 2 меньше, чем 4.
Зафиксируем эти правила коротко и емко.
1. Если а меньше b и b меньше с, то а меньше с
2. Если a больше b и b больше с, то а больше с
3. Если а равно b и b равно с, то а равно с
Более подробно про отношения говорят на курсах высшей математики, дискретной математики или математической логики, но при этом бояться таких абстрактных понятий не стоит.
Теперь мы можем применить это мощное свойство к сравнению чисел с разными знаками.
Мы знаем, что отрицательные числа меньше нуля.
Также мы знаем, что положительные числа больше или, другими словами, нуль меньше положительных чисел.
Тогда, зная транзитивность отношения «меньше», мы можем прийти к выводу, что a меньше с.
Заметьте, что мы нигде ни для а, ни для с не предполагали конкретных значений, а значит, любое отрицательное число меньше любого положительного.
Те же самые рассуждения можно провести в обратную сторону и получить, что любое положительное число больше любого отрицательного.
Итак, посмотрим, как происходит процесс сравнения чисел с разными знаками на практике.
Пример 1
Сравним \(\mathbf<-5>\) и \(\mathbf<3>\).
\(\mathbf<-5>\)- отрицательное число, \(\mathbf<3>\)— положительное.
Пройти тест и получить оценку можно после входа или регистрации
Сравнение дробей: правила, примеры, решения
Данная статья рассматривает сравнение дробей. Здесь мы выясним, какая из дробей больше или меньше, применим правило, разберем примеры решения. Сравним дроби как с одинаковыми, так и разными знаменателями. Произведем сравнение обыкновенной дроби с натуральным числом.
Сравнение дробей с одинаковыми знаменателями
Отсюда следует правило сравнения дробей с одинаковыми знаменателями: из имеющихся дробей с одинаковыми показателями считается большей та дробь, у которой числитель больше и наоборот.
Это говорит о том, что следует обратить внимание на числители. Для этого рассмотрим пример.
Сравнение дробей с разными знаменателями
Сравнение таких дробей можно соотнести со сравнением дробей с одинаковыми показателями, но имеется различие. Теперь необходимо дроби приводить к общему знаменателю.
Если имеются дроби с разными знаменателями, для их сравнения необходимо:
Рассмотрим данные действия на примере.
Ответ: 5 18 > 23 86 .
Сравнение дробей с одинаковыми числителями
Если дроби имеют одинаковые числители и разные знаменатели, тогда можно выполнять сравнение по предыдущему пункту. Результат сравнения возможет при сравнении их знаменателей.
Имеется правило сравнения дробей с одинаковыми числителями: из двух дробей с одинаковыми числителями больше та дробь, которая имеет меньший знаменатель и наоборот.
Рассмотрим на примере.
Решение