Что значит совместные события
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.
Что значит совместные события
Рассмотрим два случайных события A и B. И определим третье событие C как
Тогда событие C можно трактовать как или появление события A или появление события B в ходе эксперимента. Вообще союз «или» в теории вероятностей можно (но очень внимательно) трактовать как сложение в математическом смысле. Рассмотрим примеры суммы двух случайных событий. Допустим, бросается игральный кубик и рассматриваются события
Тогда событие C=A+B будет трактоваться как выпадение или числа 2 или числа 5 при бросании игрального кубика. Здесь следует отметить один важный момент: число 2 и 5 одновременно выпасть на одном игральном кубике не могут, а следовательно, и события A и B одновременно не могут произойти. В теории вероятностей события, которые не могут произойти одновременно в ходе эксперимента, называют несовместными.
Второй пример. Бросаются два игральных кубика и рассматриваются такие же события:
В этом случае событие A и B могут произойти одновременно в эксперименте, поэтому такие события называются совместные. Совместные и несовместные события можно условно изобразить графически следующим образом:
Эти рисунки наглядно показывают особенность расчета суммы вероятности двух совместных и несовместных событий. Вероятность суммы событий A и B условно будет равна доли площади, занимаемой множествами A и B, по отношению к общей площади всех возможных исходов опыта. Тогда получается, что для несовместных событий


Что значит совместные события
Давайте вернемся к нашей игре в дартс «в слепую», когда игрок бросает дротики с закрытыми глазами в мишень на стене так, что они равномерно распределяются по всей ее поверхности и не вылетают за пределы. Но теперь мишеней будет две (рис. 5), для которых определим два таких случайных события:
A: дротик попал в первую мишень;
B: дротик попал во вторую мишень.
Рис. 5. Красные точки – следы от дротиков; синий круг (A) – первая мишень; синий круг (B) – вторая мишень; прямоугольник (W) – фрагмент стены.
Из рисунка наглядно видно, что бросая дротик, он может попасть или в мишень A, или в мишень B, или в стену. И не может возникать ситуаций, когда дротик одновременно попадает и в мишень A и в мишень B. То есть, события A и B не могут происходить одновременно при однократном бросании дротика. В теории вероятностей такие события называют несовместными.
Итак, события называются несовместными, если в ходе проведения эксперимента они не могут происходить одновременно.
Теперь повесим мишени так, чтобы они пересекались (рис. 6). И если дротик попадает в их пересечение, то это будет означать, что он попал в обе мишени. Это означает, что те же два события A и B здесь уже могут происходить одновременно, а значит, они становятся совместными.
События называются совместными, если в ходе проведения эксперимента они могут происходить одновременно.
Рис. 6. Красные точки – следы от дротиков; синий круг (A) – первая мишень; синий круг (B) – вторая мишень; прямоугольник (W) – фрагмент стены.
Обратите внимание на слово «могут». Совместные события не обязательно происходят одновременно в каждом эксперименте. Они, также как и несовместные, могут появляться и по отдельности. И, как правило, лишь в некоторых случаях происходят совместно.
Чтобы лучше понять, какие события следует относить к совместным, а какие – к несовместным, приведем несколько примеров из задач по ЕГЭ.
Пример 1. Предположим, однократно бросается игральный кубик и рассматриваются два события:
A: выпадение числа 2;
B: выпадение числа 5.
Очевидно, что когда кубик бросается один раз, то сразу две его грани выпасть не могут, значит, события A и B не происходят одновременно, следовательно, они несовместные.
А вот если в эксперименте бросаются сразу два игральных кубика, то на одном из них вполне может выпасть число 2, а на другом – число 5. Значит, при такой постановке задачи события A и B становятся совместными.
Пример 2. Имеется фонарь с тремя одинаковыми лампами. Требуется найти вероятность того, что все три лампы не перегорят в течение года. Для решения вводятся три случайных события:
A: первая лампа перегорит в течение года;
B: вторая лампа перегорит в течение года;
C: третья лампа перегорит в течение года.
Являются ли эти события совместными или несовместными? Конечно, они совместные, так как в течение года могут перегореть все три лампы, а значит, произойдут все три события. Но если события сформулировать вот так:
A: первая лампа перегорит в течение первого года;
B: вторая лампа перегорит в течение второго года;
C: третья лампа перегорит в течение третьего года.
То при рассмотрении периода в один год события становятся несовместными, так как в течение года может произойти только событие A.
Обратите внимание, как изменение формулировок событий одной и той же задачи приводит к кардинальному изменению их свойств. Это одна из многих причин, по которой задачи по теории вероятностей нужно очень внимательно читать и также внимательно прописывать ход их решения.
1.2.2. Совместные и несовместные события.
Противоположные события. Полная группа событий
События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий. Простейшим примером несовместных событий является пара противоположных событий. Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой наверху:
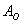
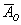
Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.
Противоположные события легко формулируются из соображений элементарной логики:
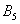
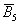
Либо 5, либо не 5, т.е. данные события несовместны и противоположны.
Аналогично:
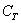
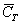
Множество несовместных событий образуют полную группу, если в результате отдельно взятого испытания обязательно появится одно и только одно из этих событий. Очевидно, что любая пара противоположных событий, например, 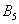
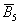
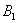
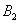
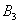
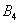
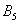
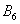
События 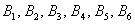
И из этих двух примеров вытекает ещё одно важное понятие, которое нам потребуется в дальнейшем – это элементарность исхода (события). Если совсем просто, то элементарное событие нельзя «разложить на другие события». Например, события 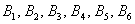
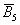
В примере с картами события 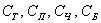
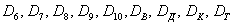
Таким образом, элементарным исходом здесь считается лишь извлечение какой-то конкретной карты, и 36 несовместных элементарных исходов тоже образуют полную группу событий.
И коротко о событиях совместных. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого. Например:
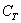
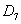
– данные события совместны, т.к. при излечении семёрки треф одновременно имеют место оба события.
Понятие совместности охватывает и бОльшее количество событий:
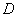
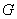
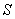
Ситуация, конечно, редкая, но совместное появление всех трёх событий, не исключено. Следует отметить, что перечисленные события совместны и попарно.
Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!
С наилучшими пожеланиями, Александр Емелин
Теория вероятности. Часть 2
В заданиях ЕГЭ по математике встречаются и более сложные задачи на вероятность (нежели мы рассматривали в части 1), где приходится применять правило сложения, умножения вероятностей, различать совместные и несовместные события.
Совместные и несовместные события
События называются несовместными, если появление одного из них исключает появление других. То есть, может произойти только одно определённое событие, либо другое.
Например, бросая игральную кость, можно выделить такие события, как выпадение четного числа очков и выпадение нечетного числа очков. Эти события несовместны.
События называются совместными, если наступление одного из них не исключает наступления другого.
Например, бросая игральную кость, можно выделить такие события, как выпадение нечетного числа очков и выпадение числа очков, кратных трем. Когда выпадает три, реализуются оба события.
Сумма событий
Суммой (или объединением) нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий.
При этом сумма двух несовместных событий есть сумма вероятностей этих событий:
Например, вероятность выпадения 5 или 6 очков на игральном кубике при одном броске, будет , потому что оба события (выпадение 5, выпадение 6) неовместны и вероятность реализации одного или второго события вычисляется следующим образом:
Вероятность же суммы двух совместных событий равна сумме вероятностей этих событий без учета их совместного появления:
Например, в торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдем вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов (то есть или в одном, или в другом, или в обоих сразу).

Вероятность совместной реализации первых двух событий по условию равна 0,12.
Значит, вероятность того, что к концу дня кофе закончится хотя бы в одном из автоматов есть
Зависимые и независимые события
Два случайных события А и В называются независимыми, если наступление одного из них не изменяет вероятность наступления другого. В противном случае события А и В называют зависимыми.
Например, при одновременном броске двух кубиков выпадение на одном из них, скажем 1, и на втором 5, – независимые события.
Произведение вероятностей
Произведением (или пересечением) нескольких событий называется событие, состоящее в совместном появлении всех этих событий.
Если происходят два независимых события А и В с вероятностями соответственно Р(А) и Р(В), то вероятность реализации событий А и В одновременно равна произведению вероятностей:
Например, нас интересует выпадение на игральном кубике два раза подряд шестерки. Оба события независимы и вероятность реализации каждого из них по отдельности – . Вероятность того, что произойдут оба эти события будет вычисляться по указанной выше формуле:
.
Подборку задач на отработку темы смотрите здесь.




