Что значит совместить наложением отрезки

Сравнение отрезков

Одной из простейших геометрических фигур является отрезок. Для того чтобы сравнивать отрезки, можно использовать два способа:

Метод наложения:

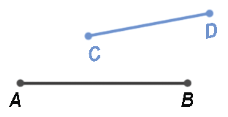
Пусть нам даны два отрезка AB и СD:

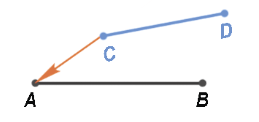
Совместим начало отрезка AB и СD (точки A и С).

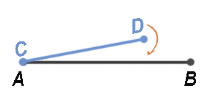
Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок ST так, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

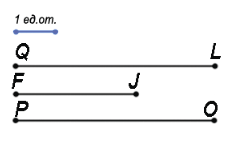
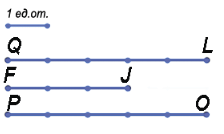
Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

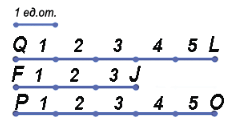
Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Поделись с друзьями в социальных сетях:

Источник

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (&gt,, &lt,, =). Например, длина отрезка АБ — 2 см, а ВГ — 8 см, записываем результат сравнения так: АБ &lt, ВГ или ВГ &gt, АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Бывает так, что при наложении одного отрезка на другой ровно половина одного из них будет совмещена с другим. Точку, которая делит его на две равные части, называют серединной точкой. И если у нас есть серединная точка В, то АВ=ВБ.

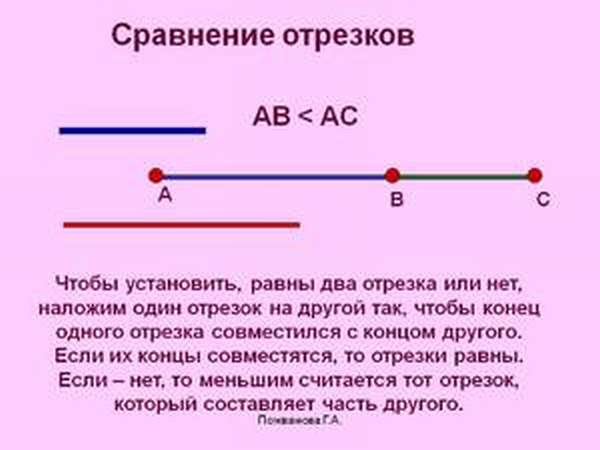
Примерно так же наложением сравнивают не только прямые, но и другие геометрические фигуры, а также углы.

Можно сделать «линейку» из полоски бумаги, при этом такую линейку не нужно линовать, достаточно отметить на ней начало и конец одного из отрезков. Затем вы прикладываете импровизированную линейку ко второму, совмещая его начало с первой отметкой и, сравниваете расположение второй отметки по отношению к его концу. Таким способом можно сравнивать и довольно большие фигуры, например, расстояние между столбиками забора, но использовать при этом лучше не бумажную полоску, а веревку.

Два отрезка называются равными, если их можно совместить методом наложения. Если есть возможность приложить их друг к другу, просто посмотрите, какой из них длиннее. Но так можно сделать не всегда.

Если под рукой имеется циркуль, поставьте одну ножку циркуля в начало, а другую в конец первого отрезка. Затем не сдвигая ножки циркуля, установите одну из них в начало второго и посмотрите, если вторая ножка циркуля в точке, обозначающей конец — они равны. Если вторая ножка на самой прямой — первый отрезок меньше, если за ним — первый больше.

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1, Х2, Y2) и b (Х3, Y3, X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 &gt, √ 73, значит, Da &gt, Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

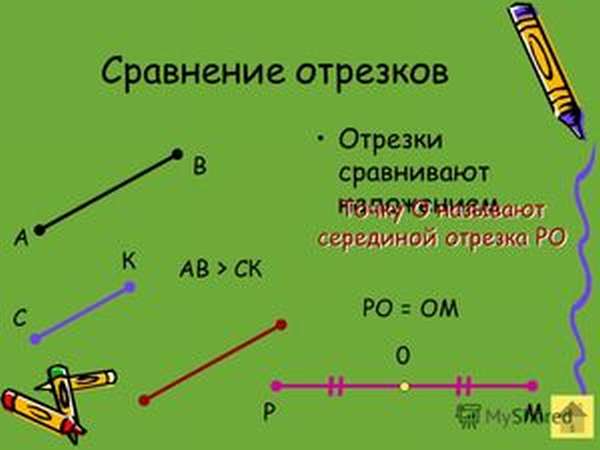
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ&lt, ВГ, а если при наложении оба конца отрезков совмещаются — значит, они равны.

Теперь рассмотрим сравнение отрезков путем измерения. При помощи линейки вычисляем длину каждого отрезка. Например, длина AB = 2 см, а CD = 8 см. 8&gt,2, значит, CD&gt,AB, то есть отрезок CD длиннее AB.

Источник

Как сравнить два отрезка: способы и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Обратите внимание: что такое луч в геометрии.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Сравнение в координатной сетке

Допустим, что у нас есть два отрезка, координаты которых мы знаем — а (Х1, Y1; Х2, Y2) и b (Х3, Y3; X4, Y4).

Первое, что нужно сделать — придать координатам числовые значения:

Da = √ ((-7 — 3) ² + (4 — (-4)) ²) = √ (-10 ² + 8 ²) = √ 100 + 64 = √ 164

Db = √ ((-3 — 0) ² + (-5 — (-3)) ²) = √ (-3 ² + (-8) ²) = √ (9+ 64) = √ 73

√ 164 > √ 73, значит, Da > Db.

Также можно сравнить отрезки, находящиеся в трехмерной системе координат, надо учитывать не две, а три координаты каждого из них.

Примеры

Рассмотрим сравнение методом наложения. У нас имеется два отрезка — АБ и ВГ.

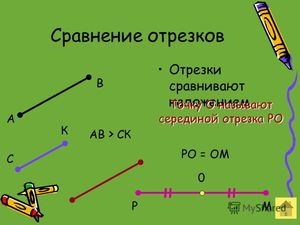
Чтобы узнать, равны они или нет, просто приложим их друг к другу так, чтобы их «начала» были в одной точке, то есть совместим точки, А и В.

Если мы видим, что АБ получается частью ВГ, значит, он меньше, то есть АБ 2, значит, CD>AB, то есть отрезок CD длиннее AB.

Источник

Наложения и движения

При наложении различные точки отображаются в различные точки.

Доказательство:

Из этого утверждения мы можем сделать вывод, что при наложении отрезок отображается на равный ему отрезок. Пусть при наложении концы А и В отрезка АВ отображаются в точки А₁ и В₁. Тогда отрезок АВ отображается на отрезок А₁В₁ (т.к. согласно аксиоме, если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки), и, следовательно, АВ=А₁В₁. Так как равные отрезки имеют равные длины, то наложение является отображением плоскости на себя, которое сохраняет расстояния, то есть любое наложение является движением плоскости.

Теорема

Доказательство

Дано: движение , АВС отображается в А₁В₁С₁, АВС=А₁В₁С₁

Доказать: движение — наложение

Доказательство:

Так как АВС=А₁В₁С₁ , то по определению существует наложение , при котором точки А, В и С отображаются в точки А₁, В₁ и С₁ соответственно. Докажем, что совпадает с .

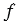
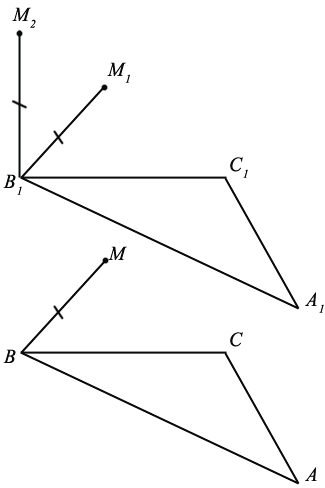
Предположим обратное. Тогда найдется хотя бы одна точка М, которая при движении отображается в точку М₁, а при наложении отображается в другую точку М₂. При отображениях и сохраняются расстояния, поэтому ВМ=В₁М₁, ВМ=В₁М₂, отсюда В₁М₁=В₂М₂, то есть точка В₁ равноудалена от точек М₁ и М₂.

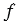
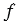
Аналогично можно доказать, что точки А₁ и С₁ равноудалены от точек М₁ и М₂. Следовательно, точки А₁, В₁, и С₁ лежат на серединном перпендикуляре к отрезку М₁М₂, но это не возможно, так как вершины А₁В₁С₁ не лежат на одной прямой. Значит, наше предположение неверно и отображение совпадает с , другими словами, движение является наложением. Теорема доказана.

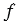
Следствие

Поделись с друзьями в социальных сетях:

Источник

Как сравнить длины отрезков?

Сравнить 2 отрезка на плоскости — это типичная задача по геометрии для учеников 7 класса. Существует несколько разных методов выполнения данного сравнения, и мы подробно расскажем о каждом из них.

Подобного рода задачи выполняются элементарно и являются основой для изучения дальнейшего материала. Стоит один раз запомнить этот несложный процесс, и в дальнейшем уже не возникнет никаких трудностей с аналогичными заданиями.

Метод наложения

Пусть нам даны два отрезка AB и СD:

Совместим начало отрезка AB и СD (точки A и С).

Затем повернем отрезок СD так, чтобы он совпал с отрезком AB.

Мы видим, что отрезок СD составляет часть отрезка AB, следовательно, мы можем сделать вывод, что отрезок AB больше отрезка СD.

Если точка делит отрезок на равные отрезки, то эту точку называют серединой отрезка.

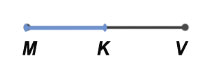
MK = KV, K — середина отрезка.

Рассмотрим еще одну пару отрезков HG и ST.

Совместим начало отрезка HG и ST.

Затем повернем отрезок STтак, чтобы он совпал с отрезком HG.

В данном случае мы видим, что совпали не только точки S и H (начала отрезков HG и ST), но и точки G и T (концы отрезков HG и ST), то есть отрезки совпадают, а нам известно, что две геометрические фигуры называются равными, если их можно совместить наложением.

Вывод:

Измерение длин:

Для измерения отрезков, необходимо наложить на него единичные отрезки, и длиннее будет считаться тот отрезок, которому соответствует большее число единичных отрезков.

Пример: Пусть у нас есть единичный отрезок. Рассмотрим три отрезка QL, FJ и PO.

Наложим единичный отрезок на данные.

Посчитаем, какое количество единичных отрезков накладывается на каждый из отрезков, получаем: QL = 5 ед.от., FJ = 3 ед.от., PO = 5 ед. от.

Сравним отрезки: QL > FJ (т.к. 5 > 3), FJ https://budu5.com/manual/chapter/3301

Как сравнить 2 отрезка: способы решения задачи

Что такое отрезок

Прежде чем рассказать, как сравнить 2 отрезка, давайте разберем, что такое отрезок на плоскости.

Определение из учебника по геометрии гласит, что отрезок — это часть прямой, которая с двух сторон ограничивается двумя точками.

Если рассматривать одну прямую, отрезком будет считаться множество, которое состоит из двух разных точек этой прямой (собственно, концов отрезка), а также остального множества из всех точек, которые располагаются между ними (так называемых внутренних точек).

Сравнение двух отрезков

Итак, в вопросе о том, как сравнить 2 отрезка, можно выделить следующие методы:

В том случае, если разность составит положительное число, значит, первый отрезок длиннее второго на соответствующее количество единиц. Если в результате получено нулевое значение — отрезки равны. А если в ответе отрицательное число, следовательно, второй отрезок длиннее первого.

Вывод

Итак, мы выяснили, как сравнить 2 отрезка. Первый способ указывает только на то, какой из них будет длиннее, а какой — короче, а второй показывает числовое значение разницы в длине.

Прямая и отрезок, измерение и сравнение отрезков

Понятие прямой, также как и понятие точки является основными понятиями геометрии. Как известно основные понятия не определяется. Это не является и исключением для понятия прямой. Поэтому рассмотрим суть этого понятия через его построение.

Возьмем линейку и, не отрывая карандаша, проведем линию произвольной длины.

Полученную линию мы и будем называть прямой. Однако тут необходимо отметить, что это не вся прямая, а только её часть. Всю же прямую построить не имеется возможным, она является бесконечной на обоих своих концах.

Прямые будем обозначать маленькой латинской буквой, либо двумя её точками в круглых скобках.

Понятия прямой и точки связаны тремя аксиомами геометрии:

Для двух прямых актуально их взаимное расположение. Возможны три случая:

В этой статье мы не будем подробно останавливаться на этих понятиях.

Отрезок

Пусть нам дана произвольная прямая и две точки, принадлежащие ей. Тогда отрезком будет называться часть прямой, которая ограничена двумя ее произвольными различными точками. Точки, которыми ограничен отрезок в рамках определения 1 называются концами этого отрезка.

Отрезки будем обозначать двумя её точками концов в квадратных скобках.

Сравнение отрезков

Рассмотрим два произвольных отрезка. Очевидно, что они могут быть либо равными, либо неравными. Чтобы разобраться в этом, нам нужна следующая аксиома геометрии.

Аксиома 4: Если оба конца двух различных отрезков совпадут при их наложении, то такие отрезки будут равными.

Итак, для сравнения выбранных нами отрезков (обозначим их отрезок 1 и отрезок 2) наложим конец отрезка 1 на конец отрезка 2, так, чтобы, отрезки оставались по одну сторону от этих концов. После такого наложения возможны два следующих случая:

Как сравнить длины отрезков: наложение и измерение, объяснение и примеры

Отрезок — часть прямой, ограниченная двумя точками, кратчайшее расстояние между этими точками. Существует несколько способов сравнения геометрических фигур, выбор такого способа зачастую зависит не только от условия задачи, но и от возможностей. Как же сравнивать отрезки, расскажем в этой статье.

Способы сравнения двух отрезков

В геометрии две фигуры, имеющие одинаковый размер и форму, называются равными. Сравнение фигур дает возможность сказать, одинаковы ли они. Одним из способов является наложение. Если фигуры удается совместить наложением, они считаются равными.

Сравнить фигуры — значит, определить, которая из них длиннее или короче. Ответ должен быть определенным, нельзя сказать, что один отрезок длиннее или равен второму. В математике такой ответ неправилен, его можно приравнять к отсутствию ответа.

Записывают результат сравнения с помощью знаков больше, меньше и знака равенство (>; АБ.

Это интересно: как разложить на множители квадратный трехчлен?

Сравнивать фигуры можно разными способами, выбор которых зависит от возможностей или условий:

Лучше всего, если они различаются по длине визуально, и, просто посмотрев на них, вы можете сказать, который длиннее. Но так бывает не всегда.

Измерение длины

Самый простой способ — измерение. Для этого можно использовать линейку, просто измерив длину отрезка, мы поймем, который из них длиннее. Если нет линейки, но они начерчены на листе в клетку, для измерения их длин можно посчитать клетки. В одном сантиметре две клетки. Это метод сравнения измерением длин, но есть еще метод сравнения наложением.

Наложение друг на друга

Как происходит совмещение АБ и ВГ:

Источник