Что значит составить подмножество чисел
Множества,их элементы,поджмножества
Вы будете перенаправлены на Автор24
В математике совокупности объектов, объединяющие ряд объектов называют множество. Данное понятие является первичным, значит, к более простым понятиям оно не сводится.
Термин множество употребляется тогда, когда речь идет о нечисловых множествах. Например, говорят о множестве диагоналей многоугольника, о множестве точек на координатной прямой, о множестве прямых, проходящих через точку.
Виды множеств
Множества могут быть конечными и бесконечными, пустыми.
Конечным называют множество, состоящее из конечного числа элементов, но при этом конечное множество может иметь любое количество элементов.
Среди конечных множеств выделяют множество, не имеющее ни одного элемента. Такое множество называется пустым множеством.
Множество, не являющееся конечным, называют бесконечным множеством.
Подмножества
Если некоторое множество не является пустым, то из него можно выделить другие множества, которые будут являться его частями.
Например, из множества натуральных чисел можно выделить множество четных.
Обозначение множеств, подмножеств и их элементов
Готовые работы на аналогичную тему
\[38\notin А, 74\notin А,934\notin А ; 12\in A,\ <\rm :\ >54\in A.\]
Способы задания множеств
Существует два глобально различных способа задания множеств.
Первый заключается в том, что множество задается указанием всех его элементов. В таком случае говорят, что множество задано перечислением всех своих элементов или списком своих элементов. Перечислением элементов можно задать только конечные множества и при небольшом количестве элементов, входящих в него
При таком способе задания множеств говорят, что множество задано перечислением его элементов.
Равенство множеств
Множества равны в том случае, если равны их элементы. При этом если множества состоят из одних и тех же элементов, но записанных в разном порядке то эти множества различны, хотя и равны.
Например, рассмотрим множества
Эти множества будут, состоят из равных элементов, значит, они будут равны, но при этом элементы расположены в разном порядке, т.е. множества различны
Пересечение множеств
Если даны два множества, то можно образовать новое множество, составленное из общих элементов этих множеств.
Например, рассмотрим два множества:
Объединение множеств
Математически это можно обозначить так:$\ А\ \cup B$
Разность множеств
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 27 05 2021
Множество и его элементы. Подмножества
Понятие множества
Что такое «множество», мы понимаем интуитивно. В этом смысле это понятие первично, так же как «точка» или «плоскость».
Создатель теории множеств Г.Кантор описывал множество как «многое, мыслимое нами как единое».
Приведём примеры множеств:
Множество людей в салоне самолёта
Множество деревьев в парке
Множество планет Солнечной системы
Множество электронов в атоме
Множество натуральных чисел
Множество «синих-синих презелёных красных шаров»
Конечное, бесконечное и пустое множества
Людей в салоне самолёта легко посчитать, это множество конечно.
С деревьями в парке, планетами и электронами – сложней. Скорее всего, мы не сможем назвать точное количество элементов этих множеств в данный момент времени. Однако, и эти множества конечны.
Натуральное число – это идеальный объект, абстракция. Множество натуральных чисел бесконечно. Как оказалось, человек может оперировать и абстракциями, и бесконечностями.
Можно себе представить даже то, «чего на свете вообще не может быть». Поскольку таких объектов нет, их множество будет пустым. Пустое множество является частью любого другого множества.
Помидоры на грядке
Числа (натуральные, рациональные, действительные и т.д.)
Количество рациональных чисел на отрезке [0;1]
Полосатые летающие слоны
Все точки пересечения двух параллельных прямых на плоскости
Способы задания множеств
1) Перечисление – в списке задаются все элементы множества.
Множество всех континентов Земли:
Множество букв слова «математика»:
Множество натуральных чисел меньших 5:
2) Характеристическое свойство – указывается особенность элементов множества.
D =
3) Графическое изображение – визуальное моделирование с помощью различных диаграмм (круги Эйлера, интервалы, графики и т.п.)
Подмножества
Говорят, что B содержит A, или B покрывает A.
Пустое множество является подмножеством любого множества.
Множество людей является подмножеством приматов, живущих на Земле.
Множество квадратов является подмножеством прямоугольников.
Множество всех подмножеств данного множества A называют булеаном или степенью множества A.
Примеры
Пример 1. Запишите данное множество с помощью перечисления элементов:
Задано множество целых чисел, квадрат которых меньше 5. Перечисляем:
Задано множество целых чисел, модуль которых не больше 3. Перечисляем:
Задано множество рациональных чисел, являющихся корнями уравнения
(x-1)(2x+5) = 0. Перечисляем:
Пример 2. Запишите данное множество с помощью характеристического свойства:
а) Множество всех натуральных чисел меньше 10
б) Множество всех действительных чисел, кроме 0
в) Множество всех точек с целыми координатами, принадлежащих прямой y = 2x+1
Пример 3. Изобразите на графике в координатной плоскости данное множество:
Задано конечное множество точек, которое можно представить перечислением:
Пример 4. Укажите и запишите с помощью перечисления одно из непустых конечных подмножеств для данного множества:
Множества
Множество — это совокупность любых объектов. Множества обозначают большими буквами латинского алфавита — от A до Z.
Основные числовые множества: множество натуральных чисел и множество целых чисел, всегда обозначаются одними и теми же буквами:
N — множество натуральных чисел,
Z — множество целых чисел.
Множества делятся на конечные и бесконечные. Конечное множество — множество, содержащее определённое (конечное) количество элементов. Бесконечное множество — множество, содержащее бесконечно много элементов. К бесконечным множествам можно отнести множества натуральных и целых чисел.
Для определения множества используются фигурные скобки, в которых через запятую перечисляются элементы. Например, запись
означает, что множество L состоит из четырёх чётных чисел.
Термин множество употребляется независимо от того, сколько элементов оно содержит. Множества не содержащие ни одного элемента называются пустыми.
Подмножество
Подмножество — это множество, все элементы которого, являются частью другого множества.
Визуально продемонстрировать отношение множества и входящего в него подмножества можно с помощью кругов Эйлера. Круги Эйлера — это геометрические схемы, помогающие визуализировать отношения различных объектов, в нашем случае, множеств.
Рассмотрим два множества:
Каждый элемент множества L принадлежит и множеству M, значит, множество L является подмножеством множества M. Такое соотношение множеств обозначают знаком ⊂ :
Рассмотрим два множества:
Так как оба множества состоят из одних и тех же элементов, то L = M.
Пересечение и объединение множеств
Из данного примера следует, что пересечением множеств называется множество, которое содержит только те элементы, которые встречаются во всех пересекающихся множествах.
При объединении равных множеств объединение будет равно любому из данных множеств:
Разнообразие бесконечностей
Бесконечные множества содержат неограниченную последовательность элементов, объединенных общим признаком. Самые часто используемые из них в математике:
Все они бесконечны, вовсе не означает, что они равномощны.
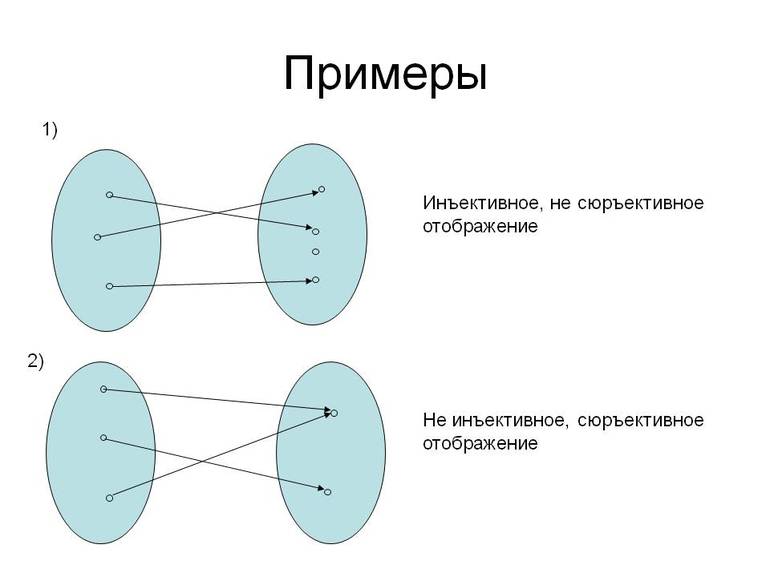
Сравнение и отображение
Числа в математике можно сравнивать друг с другом и выяснять, какое из них больше. С множествами можно производить аналогичные действия. Это будет называться их отображение друг в друга. Оно может быть дизъюнктивно, конъюнктивно и биективно. Это аналог числовых понятий «больше», «меньше» и «равно». Для того чтобы разобраться, как происходит это сравнение, нужно понятие подмножества.
Подмножеством некоторого набора компонентов называется любая часть компонентов этого набора. То есть, совокупность состоящее из чисел 1 и 3 является подмножеством множества чисел 1, 3 и 5. А они оба, в свою очередь, являются подмножествами совокупности нечётных чисел и т. д.
Если каждому компоненту множества A можно сопоставить какой-то элемент подмножества совокупности В, то отображение А в В конъюнктивно или А меньше, чем В. Если при этом нельзя найти в наборе А подмножество, которое можно сопоставить с совокупностью В, то отображение В в А дизъюнктивно. Если же каждому компоненту из комплекса А можно сопоставить элемент из совокупности В и каждому компоненту из набора В можно сопоставить элемент из совокупности А, то эти множества отображаются друг в друге биективно. В таком случае говорят, что они эквивалентны.
Для сравнения совокупностей можно использовать их мощность. Если мощность А меньше мощности В, то и множество А меньше, чем В. Если мощности равны, то сами наборы элементов эквивалентны.
Сопоставление наборов элементов
Казалось бы, используя свойства сравнения наборов элементов, можно найти соотношение мощностей бесконечных совокупностей. Ведь очевидно, что множество N является подмножеством совокупности Z, они оба являются подмножеством Q, а множества Q и I вместе составляют R. И отсюда, по определению, следует, что мощности соотносятся так: |N| |I|, и загадкой остается только соотношение совокупностей Q и I. Но всё не так просто.
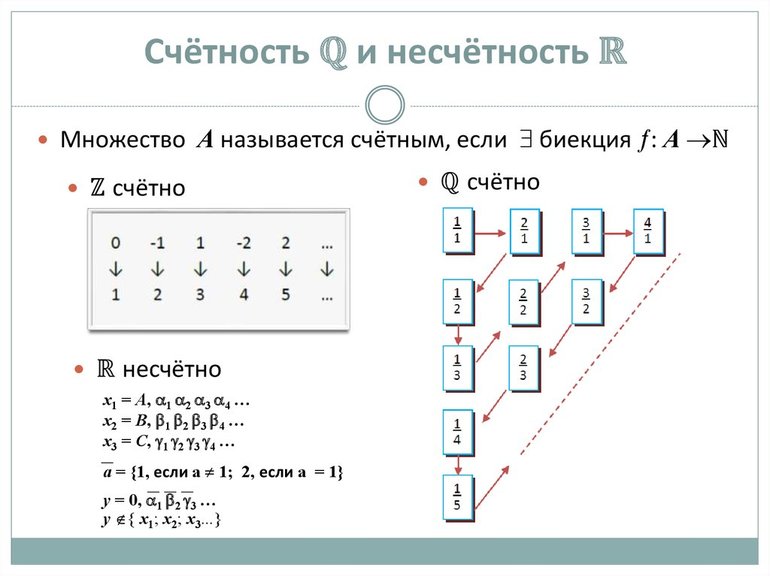
Выяснение размера бесконечного комплекса компонентов — такая же задача, как определение размера конечной совокупности — пересчёт компонентов. Возможность посчитать и пронумеровать элементы бесконечной совокупности называется счётностью. Совокупность натуральных чисел — счётная. Элементам в этом случае легко присвоить порядковые номера. И все множества, которые эквивалентны N, тоже будут счётными. Его размер |N| = a.
Но если взять R, то его элементы пронумеровать не получится. Ведь между любыми двумя точками, а прямой всегда можно поставить ещё одну. То есть, совокупность R «бесконечна вглубь»: каждый промежуток между бесконечным количеством точек содержит в себе бесконечное количество точек. Значит, свойство R — несчётность. Такие «бесконечные вглубь» множества называют континуальными. И их мощность обозначается как |R| = c.
Ещё одно важное свойство бесконечных множеств заключается в том, что если из бесконечной совокупности удалить (или добавить к ней) подмножество меньшей мощности, то размер исходной совокупности сохранится. Если из N убрать все числа от 1 до 10, то его мощность не уменьшится на 10, а останется прежней. Множество останется бесконечным и счётным: a — 10 = a.
Бесконечная мощность счётных и несчётных множеств может быть описана тремя формулами. Это два равенства и одно неравенство:
Совокупность всех точек интервала или отрезка на прямой тоже будет континуальна, так как на неё можно спроецировать всю совокупность точек действительной прямой R.
Соотношение мощностей
Континуальное множество больше счётного. Но какова их разница? Чтобы это вычислить, потребуется понятие булеан.
Что такое булеан
Есть некий набор компонентов V. Булеаном V будет называться комплекс всех его подмножеств. Как будут соотноситься размер булеана и самого V? Если V состоит из одного элемента, то его булеан будет состоять из двух элементов: пустого набора компонентов и самого V. Если V состоит из двух элементов, то булеан содержит 4 элемента: пустое множество, V и каждый из двух элементов. Если V содержит 3 элемента, то булеан содержит 8: пустое, само V, каждый из трёх его элементов в отдельности и каждую пару элементов (которых тоже три).
То есть мощность булеана — это 2 в степени размера самого V. Булеан так и записывается 2^|V|. Размер булеана всегда будет больше, чем мощность самой совокупности.
Результат сопоставления
Размер булеана любой счётной совокупности будет 2^a. Если рассматривать N, то его булеан будет состоять из пустоты, бесконечного числа элементов N, бесконечного числа пар элементов, бессчётного числа сочетаний элементов по 3, 4, 5 и так до бесконечности. Какому известному множеству можно сопоставить этот булеан?
Так как это N — натуральные числа, то каждый элемент булеана — это последовательность чисел. Если представить каждую такую последовательность в виде знаков после запятой в десятичной дроби, то получатся координаты точек в интервале от 0 до 1, который эквивалентен R. Так как булеан N содержит бесконечное количество комбинации бесконечных десятичных дробей, то он покрывает все точки в этом интервале. Это нестрогое доказательство уравнения c = 2^a.
Обозначения мощностей а и c происходят от слов account и continum, но именно такая последовательность букв порождает вопрос: а есть ли бесконечное множество мощностью b, которое меньше c, но больше a. Если и есть, то пока они неизвестны. А вот комплекс больший по мощности, чем c, есть. Это булеан континуального множества с мощностью 2^c. А у этого булеана тоже есть булеан с ещё большей мощностью.
Бесконечные множества бывают счётными и несчётными. Счётными называют те, элементы в которых можно пересчитать, то есть эквивалентные совокупности натуральных чисел. К ним относятся само множество натуральных, а также целых и рациональных чисел. Среди несчётных выделяют континуальные множества, эквивалентные совокупности всех точек на прямой. К ним относятся действительные и иррациональные числа. Континуальность является булеаном счётного набора.
Как найти все подмножества множеств
На простом примере напомним, что называется подмножеством, какие бывают подмножества (собственные и несобственные), формулу нахождения числа всех подмножеств, а также калькулятор, который выдает множество всех подмножеств.
Пример 1. Дано множество А = <а, с, р, о>. Выпишите все подмножества
данного множества.
Решение:
Несобственные: <а, с, р, о>, Ø.
Всего: 16 подмножеств.
Пояснение. Множество A является подмножеством множества B если каждый элемент множества A содержится также в B.
• пустое множество ∅ является подмножеством любого множества, называется несобственным;
• любое множество является подмножеством самого себя, также называется несобственным;
• У любого n-элементного множества ровно 2 n подмножеств.
Последнее утверждение является формулой для нахождения числа всех подмножеств без перечисления каждого.
Для математиков сформулируем теорему и приведем строгое доказательство.
1. Для n = 1 (база индукции) (и даже для n = 2, 3) теорема доказана.
Следовательно, всех подмножеств множества B: 2 k + 2 k = 2 ⋅ 2 k = 2 k+1 штук.
Теорема доказана.
В примере 1 множество А = состоит из четырех элементов, n=4, следовательно, число всех подмножеств равно 2 4 =16.
Если вам необходимо выписать все подмножества, или составить программу для написания множества всех подмножеств, то имеется алгоритма для решения: представлять возможные комбинации в виде двоичных чисел. Поясним на примере.