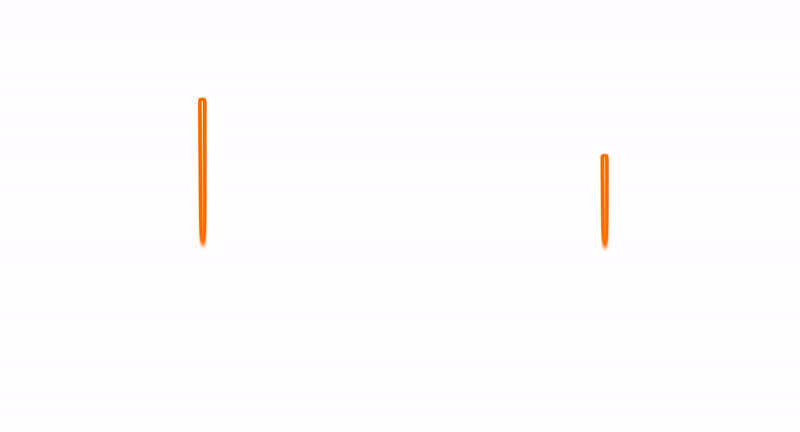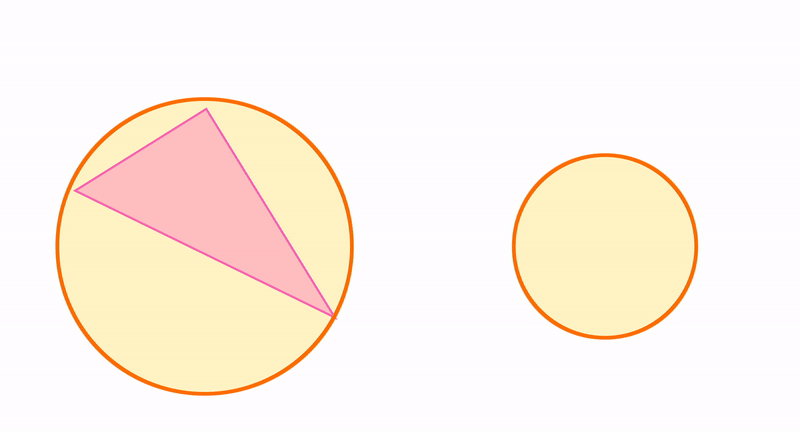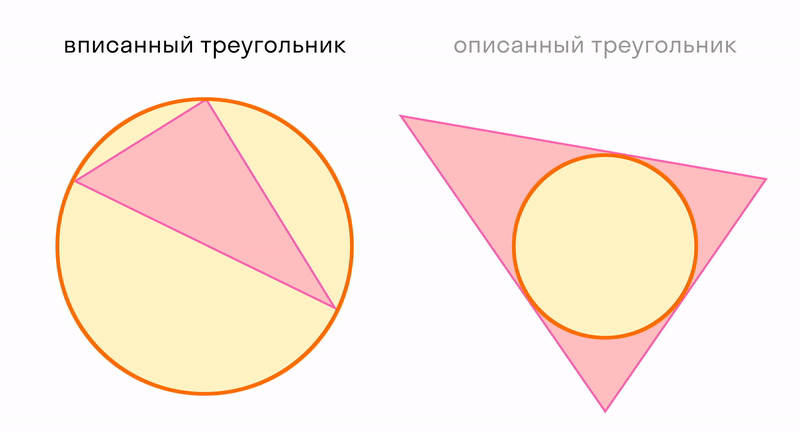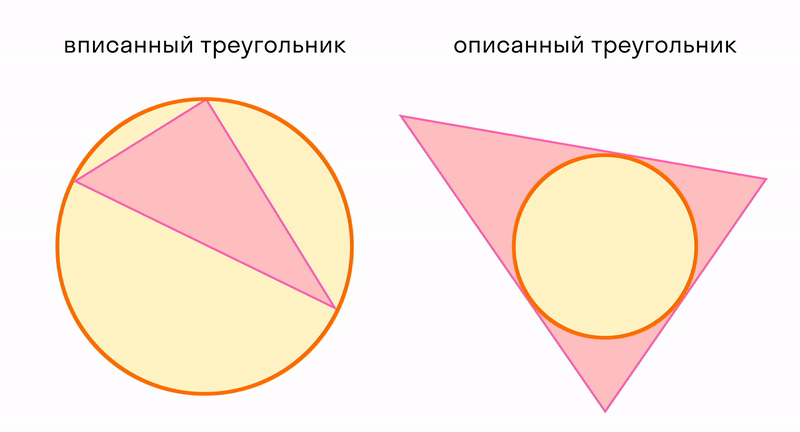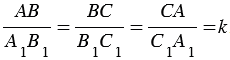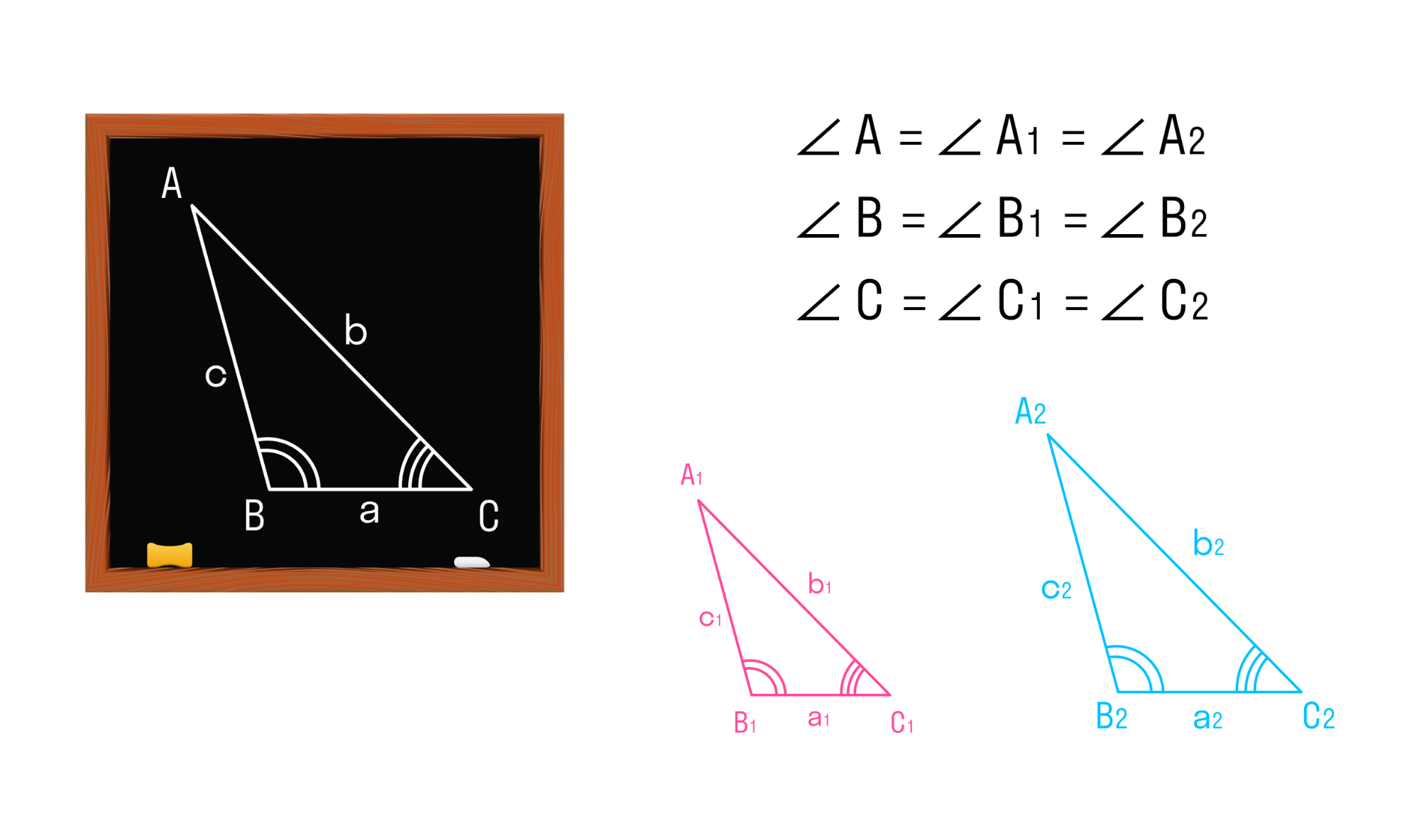Что значит смм в геометрии
Основы геометрии
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Идеальные объекты
Геометрия — раздел математики, который изучает пространственные структуры и отношения, а также их обобщения.
Основные геометрические объекты: окружность, квадрат, ромб, прямоугольник, равносторонний треугольник, равнобедренный треугольник, правильный многоугольник, эллипс и другие.
Все эти фигуры обладают двумя свойствами:
Равенство частей можно заметить у квадрата, ромба или равностороннего треугольника — равенство сторон. Также у них есть одна или несколько линий симметрии.
У шара бесконечное количество осей симметрии и плоскостей симметрии, но отсутствует равенство или подобие составных частей.
Все типы правильных многогранников обладают симметрией, при этом составлены из некоторого количества одинаковых фигур (треугольников, квадратов, пятиугольников).
Из всего этого можно сделать вывод, что отличить правильную геометрическую фигуру от произвольной совсем не сложно. Достаточно выяснить, имеет ли данная фигура оси или плоскости симметрии, а также из каких повторяющихся частей она состоит.
Таким образом, именно по наличию или отсутствию симметрии и равенства или подобия составных частей можно оценивать различные объекты окружающего мира на соответствие правильному геометрическому виду.
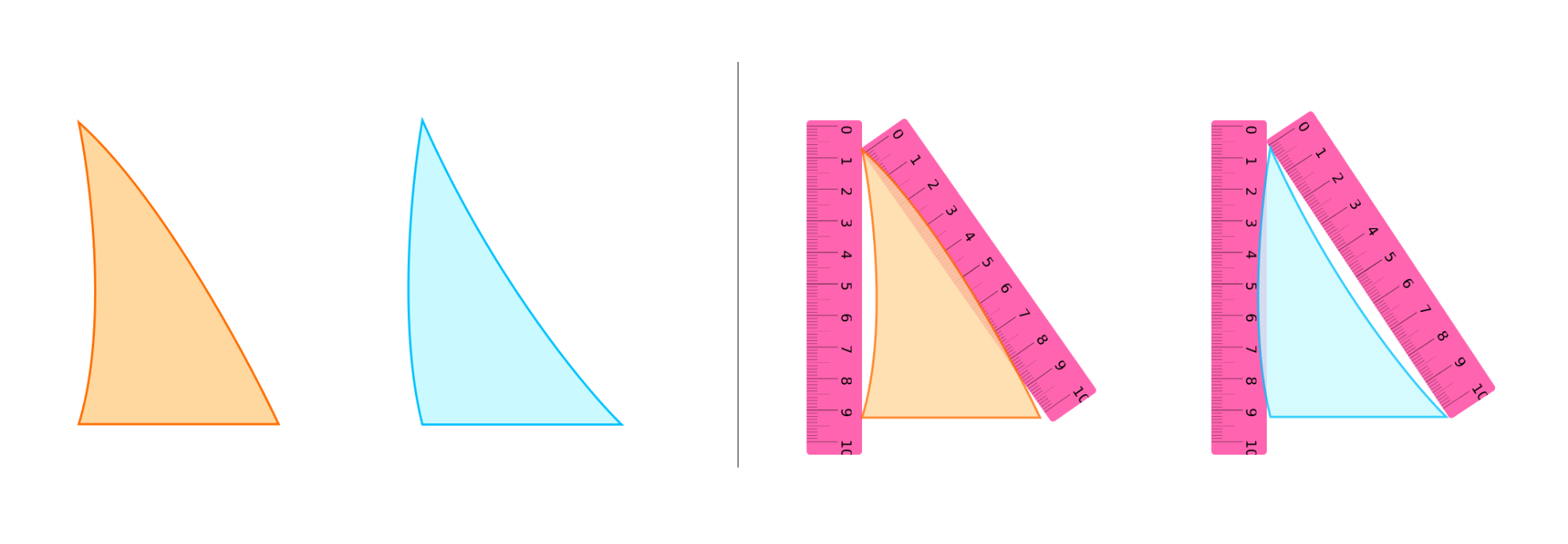
Например, возьмем два треугольника. На первый взгляд, они похожи, но у одного из них одна сторона вогнутая, вторая — выпуклая. А у другого наоборот.
Математика занимается идеальными объектами и делает о них некие заключения, которые называют теоремами. Эти треугольники похожи, и о них можно сделать близкое заключение, которое будет описывать свойства обоих.
Например, теорема Пифагора звучит так: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов. А затем это свойство можно применять при решении задач и составлении чертежей.
Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.
Базовые геометрические объекты
Базовые геометрические фигуры — это точки, отрезки, лучи, прямые, плоскости.
Точка — это идеальный математический объект, у которого нет длины и ширины.
Отрезок — это часть прямой, у которого есть начало и конец.
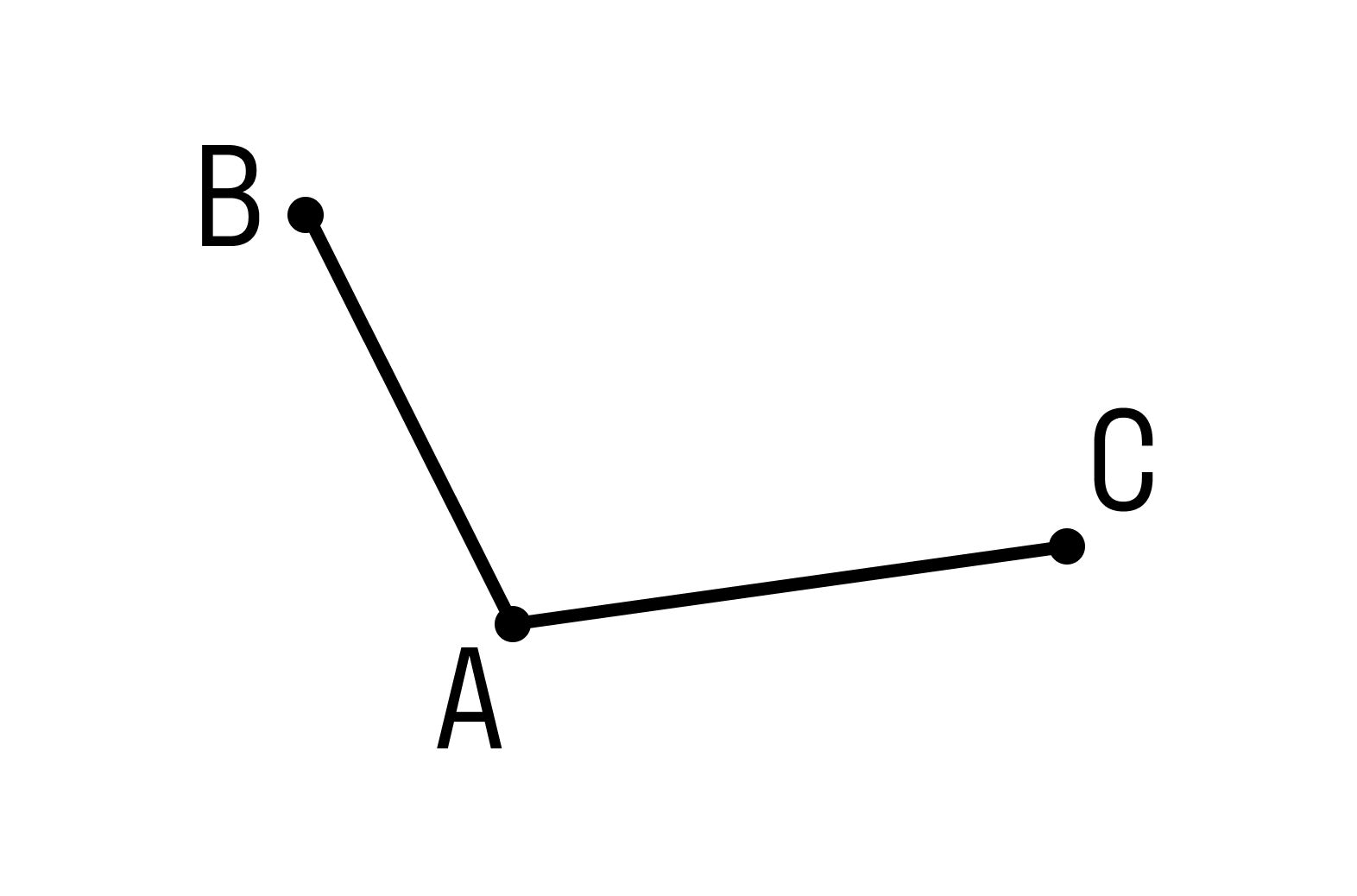
Смежные отрезки — это отрезки, которые не лежат на одной прямой и имеют один общий конец. На рисунке изобразили смежные отрезки АВ и АС, где точка А — общий конец.
Прямая — это «не кривая». Более точное определение вряд ли можно сформулировать.
Когда мы рисуем прямую на листе бумаги, мы изображаем только ее часть, потому что прямая не имеет начала и конца.
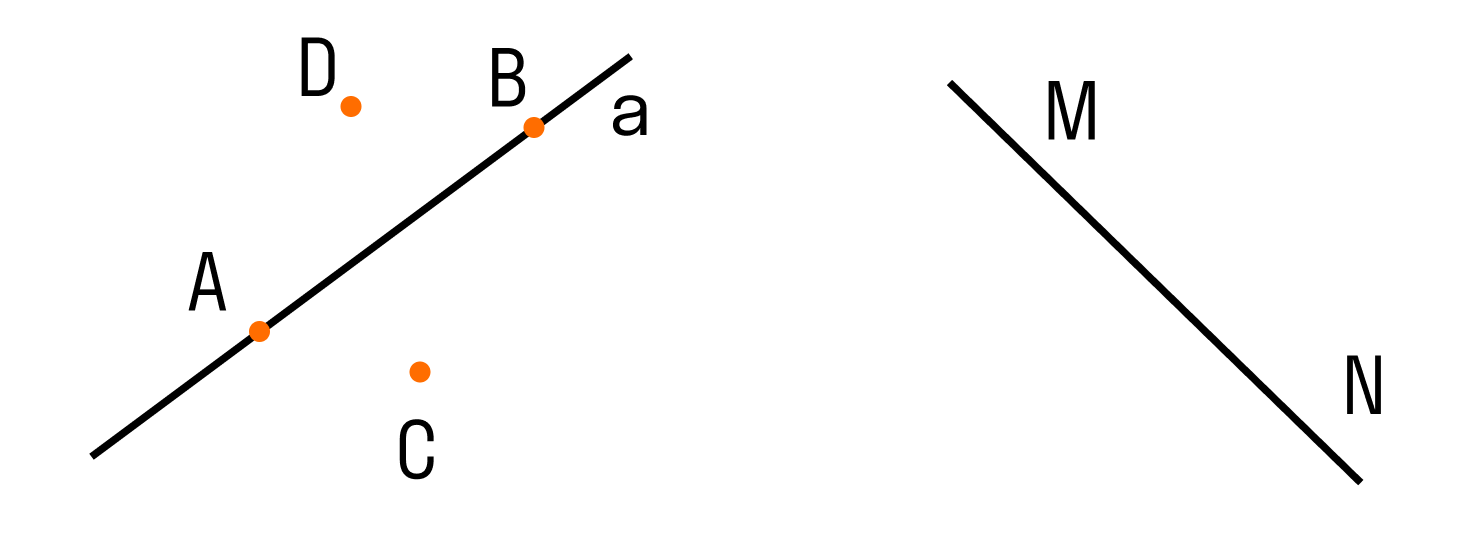
Обозначать прямые принято малыми латинскими буквами (a, b,c), но можно и большими латинскими буквами (АВ, CD, MN). Точки всегда обозначают большими латинскими буквами (А, В, С).
Два варианта расположения точек относительно прямой:
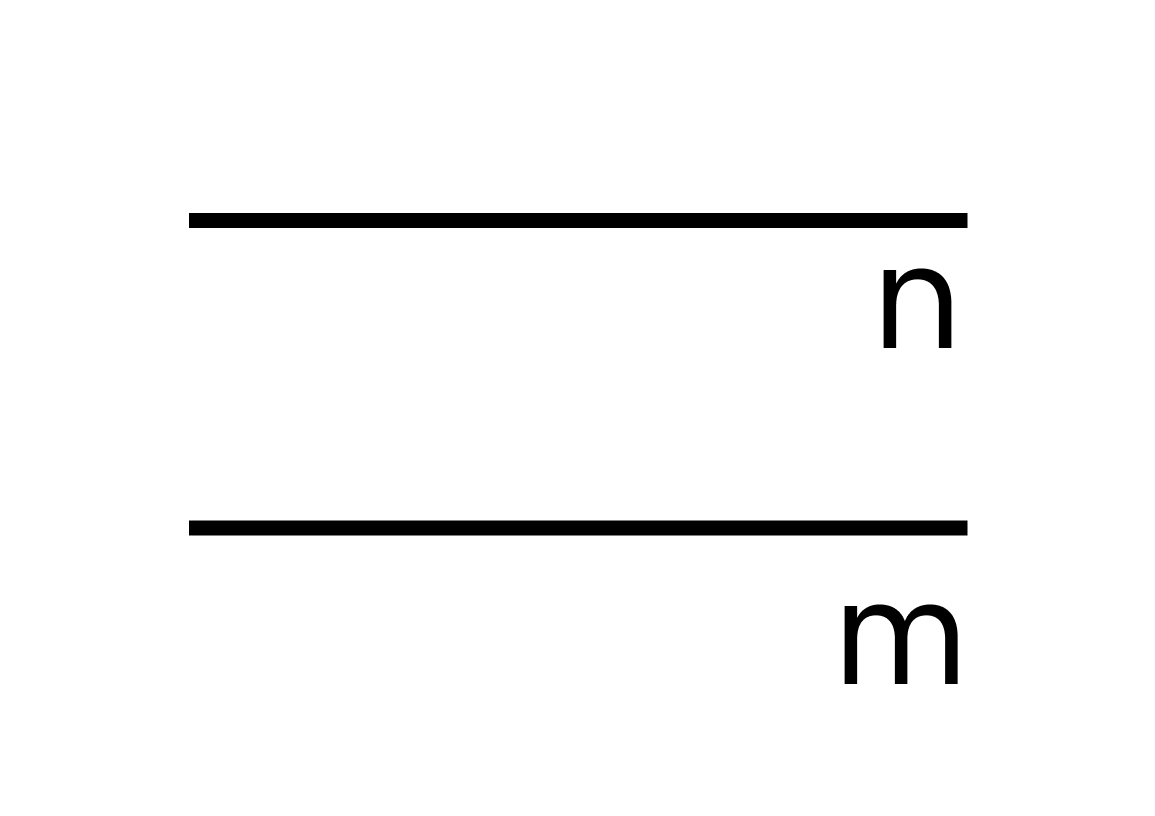
Если рассмотреть две прямые, то возможны два варианта их расположения:
Для записи не пересекающихся прямых используют специальный знак — 
то есть m 
Луч — это часть прямой, ограниченная с одной стороны. Луч имеет начало, но не имеет конца.
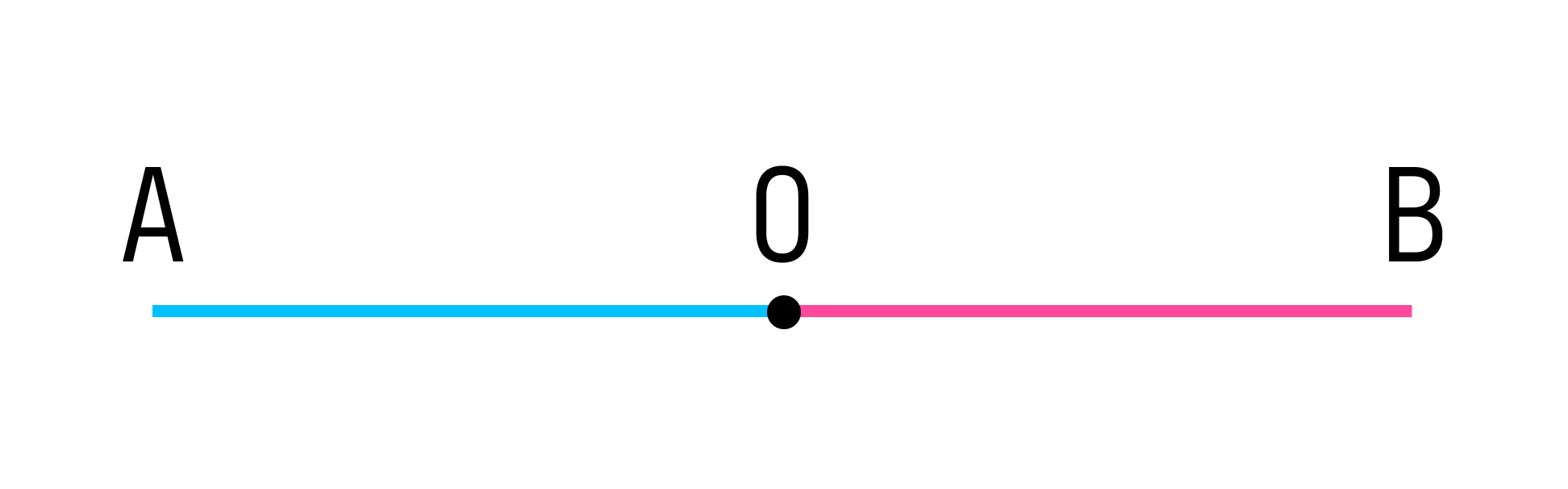
На рисунке точка О разбивает прямую АВ на две части:
Каждая из этих частей называется лучом, а точка О является началом одного и другого луча.
Назовем получившиеся лучи:
Лучи ОА и ОВ принадлежат одной прямой АВ. Лучи ОА и ОВ имеют общее начало (точка О). Лучи ОА и ОВ противоположно направлены. При таких условиях лучи ОА и ОВ называются дополнительными.
Плоскость — это бесконечная поверхность, к которой принадлежат все прямые, которые проходят через какие-либо две точки плоскости
Комбинации простейших объектов
Поговорим про комбинации простейших объектов. Например, две прямые, которые мы уже разглядели — либо пересекаются на плоскости, либо нет (тогда они параллельны).
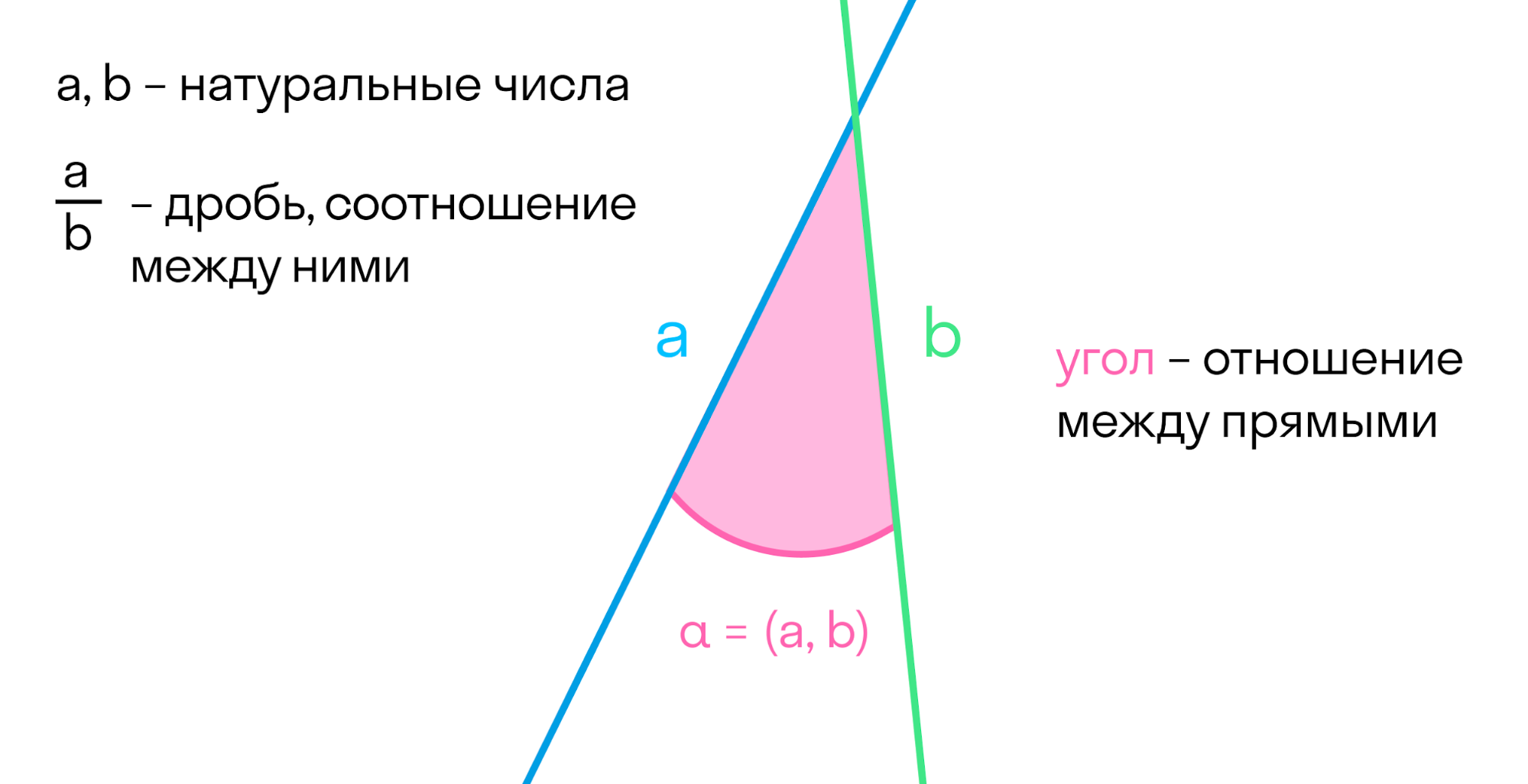
Когда прямые пересекаются, можно ввести понятие отношения между двумя прямыми. Аналогично мы поступали с числами: ввели натуральные числа — количество предметов в множестве. А после этого изучали отношения между этими числами: дроби, возведение в степень.
Точно так же мы изучали множества, а после — отношения между множествами, функции.
Две прямые образуют углы. По сути, угол — это отношение между прямыми. Если один из них нулевой, то прямые параллельны. Если нет — прямые пересекаются.
Максимальный угол – это полный оборот, он составляет 360 градусов.
Угол — это часть плоскости, ограниченная двумя лучами, которые выходят из одной точки. Углы измеряются в градусах. Углов бесконечно много, так как от 0° до 360° угол может принимать бесконечное множество значений.
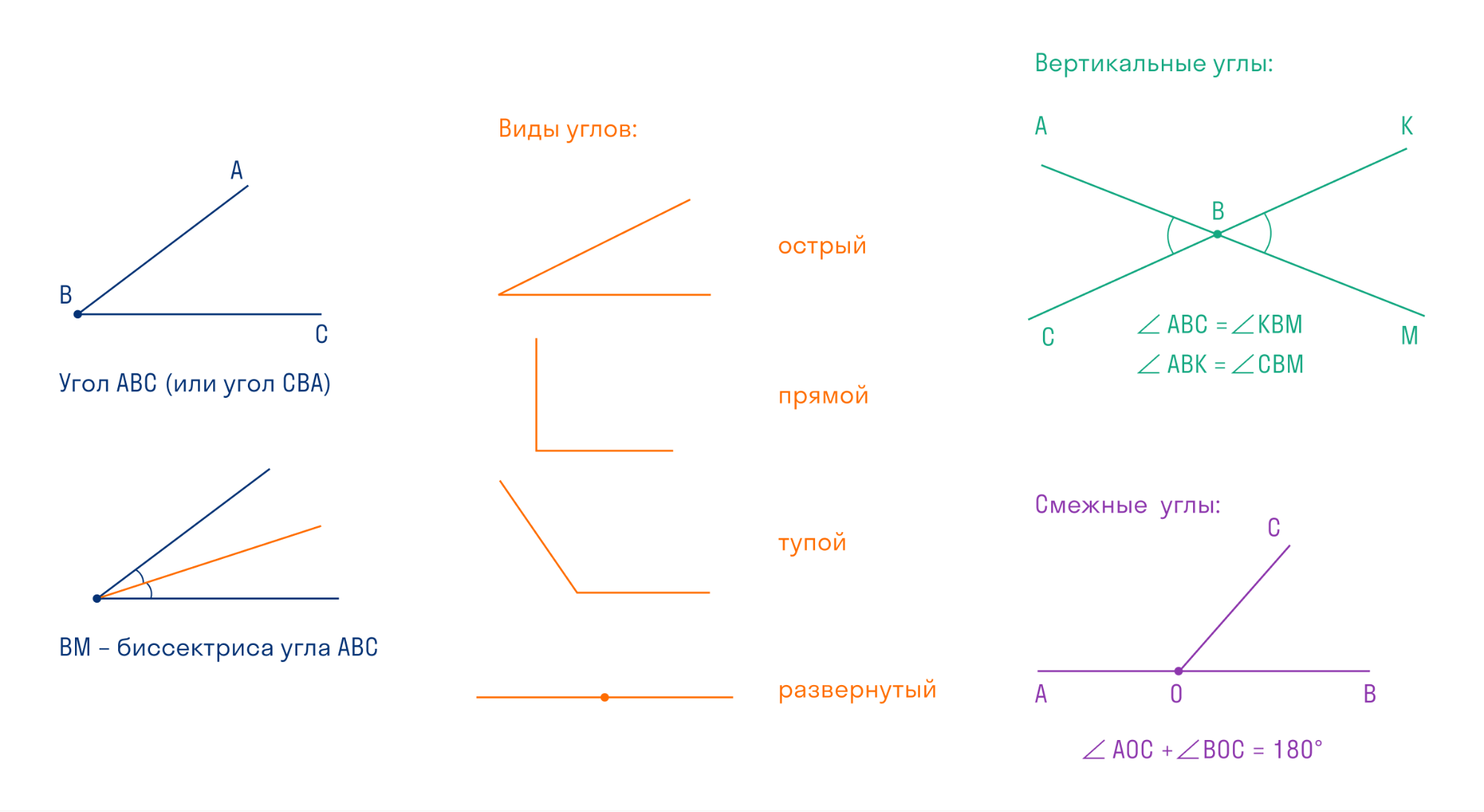
Есть разные виды углов, выделим самые часто встречающиеся:
Точка называется вершиной угла, а лучи — сторонами угла.
Два угла называются вертикальными, если их стороны являются дополнительными лучами. Свойство вертикальных углов звучит так: вертикальные углы равны.
Два угла называются смежными, если одна сторона у них общая, а две другие являются дополнительными лучами. Свойство смежных углов: сумма смежных углов равна 180°.
Биссектриса угла — это луч с началом в вершине угла, который делит угол на две равные части.
А теперь посмотрим на взаимное расположение трех прямых.
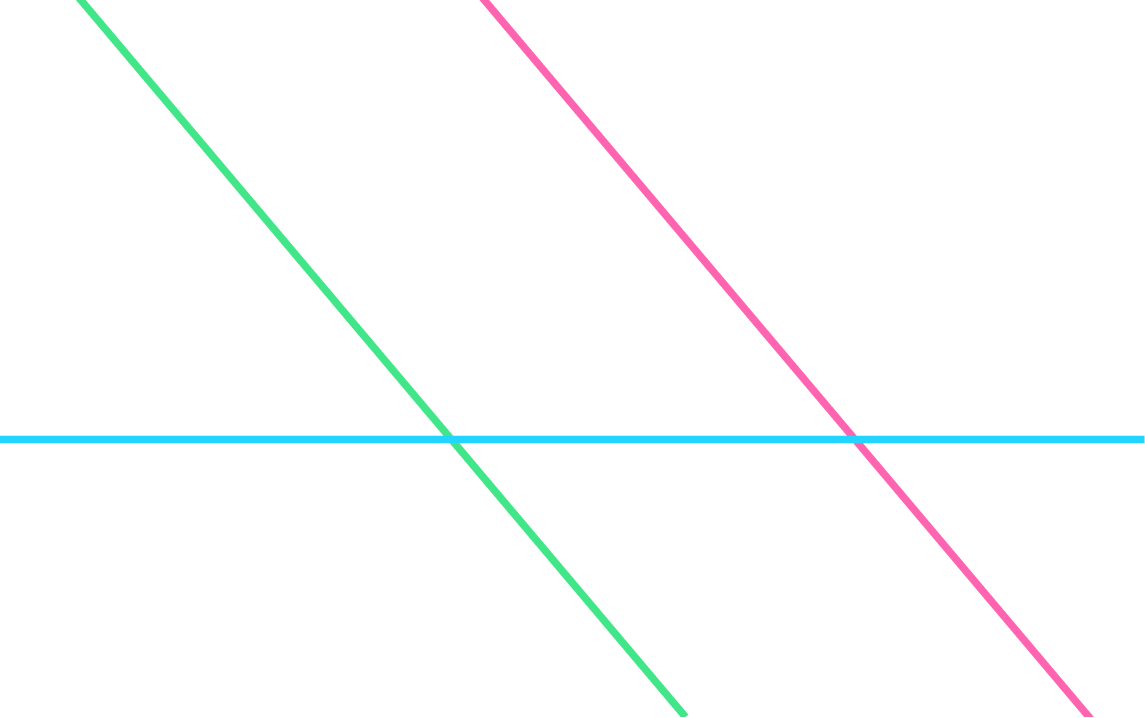
Первый случай: все три прямые параллельны.
Второй случай: две прямые параллельны, а третья их пересекает.
Третий случай: если провести три прямые на плоскости случайным образом, велика вероятность образования треугольника. Поэтому этой фигуре мы уделяем так много времени в школе на уроках геометрии.
Треугольник
Треугольник образуют три прямые. Но на треугольник также можно посмотреть, как на фигуру, которая состоит из трех отрезков.
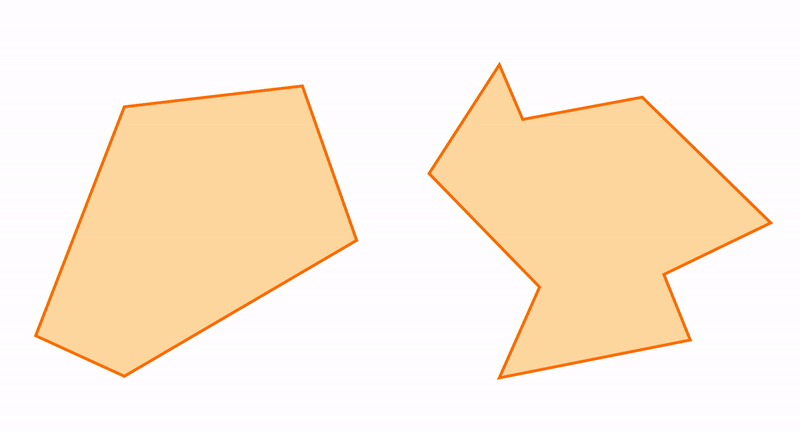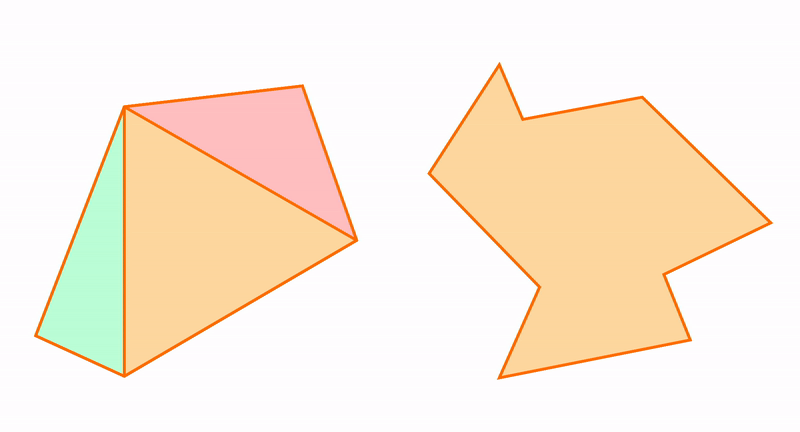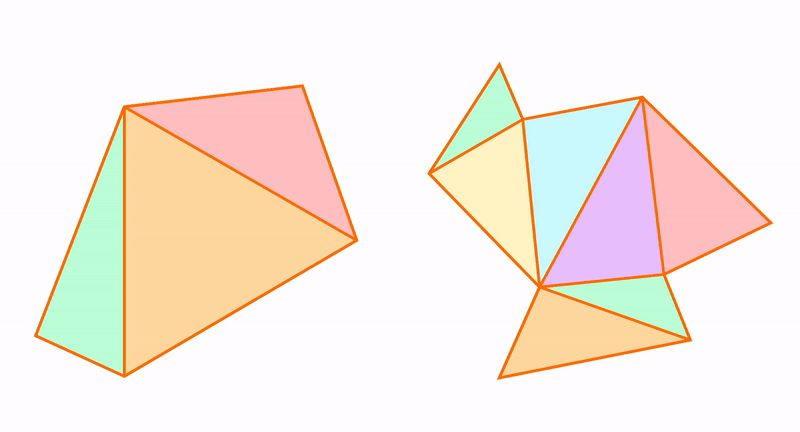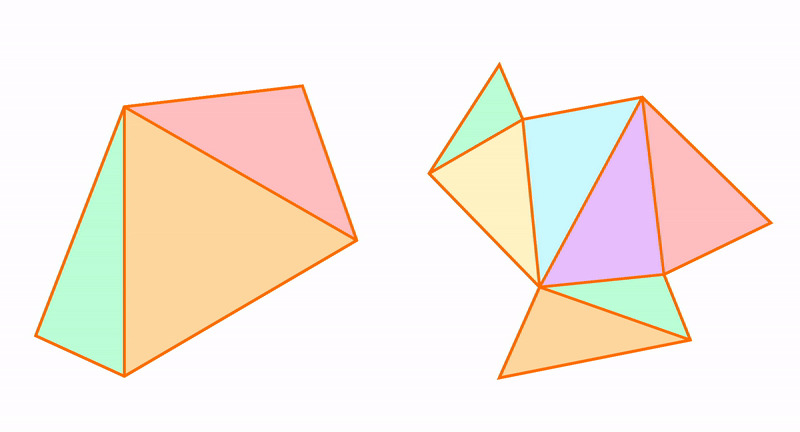
Из треугольников можно получить остальные многоугольники и к треугольникам можно приближать другие фигуры. Например, пятиугольник состоит из трех треугольников.
Треугольник можно использовать для измерения расстояний. А еще треугольник можно рассматривать в отношениях с окружностью, которая тоже является элементарной конструкцией. Читайте про вписанные и описанные углы.
Треугольник можно легко вычислить, то есть найти его площадь по трем элементам:
Приходи на наши онлайн уроки по математике с лучшими препадавателями! Для учеников с 1 по 11 классы!
Свойства треугольников
Раз треугольник можно задать тремя элементами, значит их можно классифицировать. Если два треугольника похожи, значит у них есть общие свойства.
Треугольник можно составить совсем не из любых трех отрезков: они должны удовлетворять важному свойству — неравенству треугольника.
Кратчайшее расстояние между двумя точками — это длина отрезка, который их соединяет. Из этого следует, что любой другой путь между двумя точками будет длиннее, чем этот отрезок.
Сумма любых двух сторон треугольника больше его третьей стороны.
Еще одно свойство верное для всех треугольников: сумма всех углов треугольника составляет половину полного оборота. Или по-другому: сумма углов треугольника — два прямых угла.
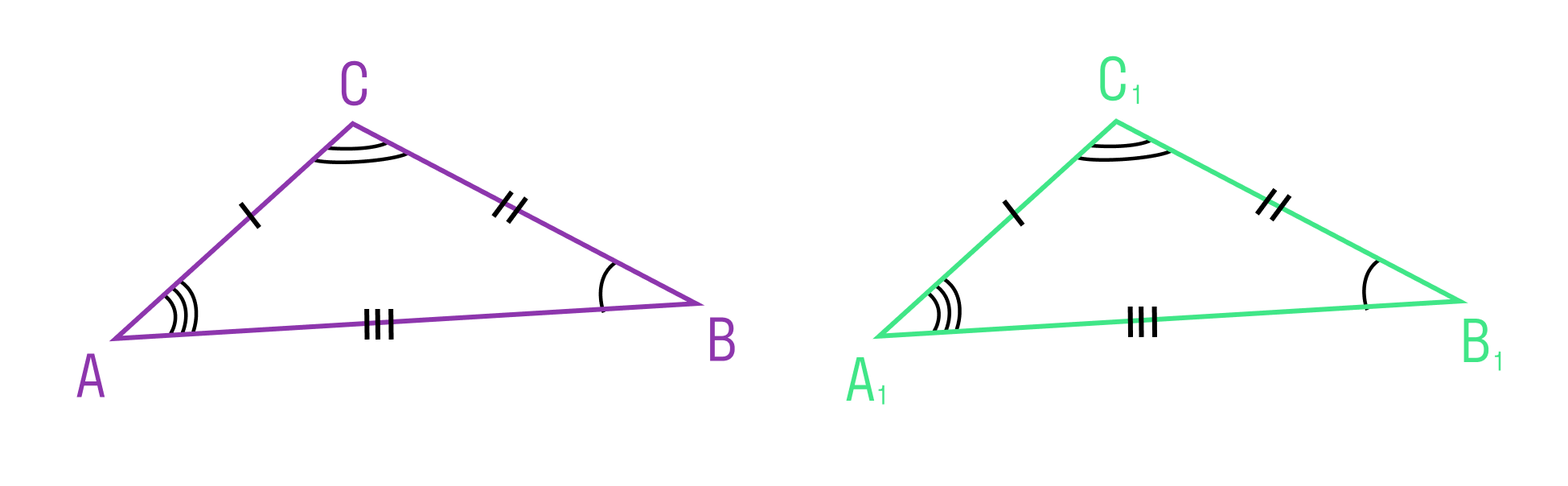
Мы знаем, что две геометрические фигуры считают равными, если их можно совместить наложением. Это справедливо и для треугольников. Равные фигуры имеют равные размеры и формы. Значит, если два треугольника равны — элементы одного треугольника соответственно равны элементам другого треугольника.
Равенство треугольников ABC и A1B1C1 обозначается так: ΔABC = ΔA1B1C1.
Есть даже специальные теоремы про равенство треугольников.
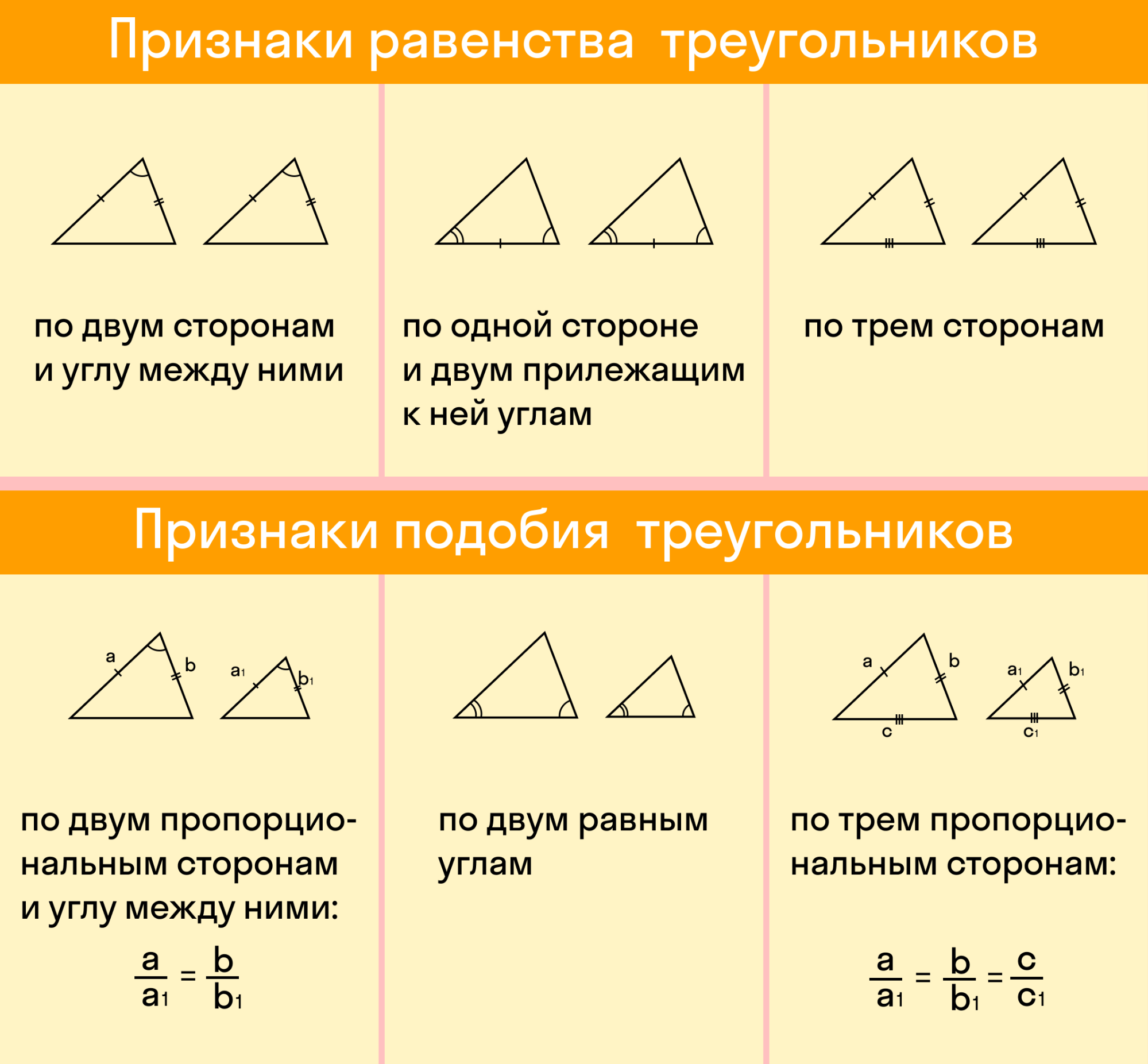
Первый признак равенства треугольников звучит так:
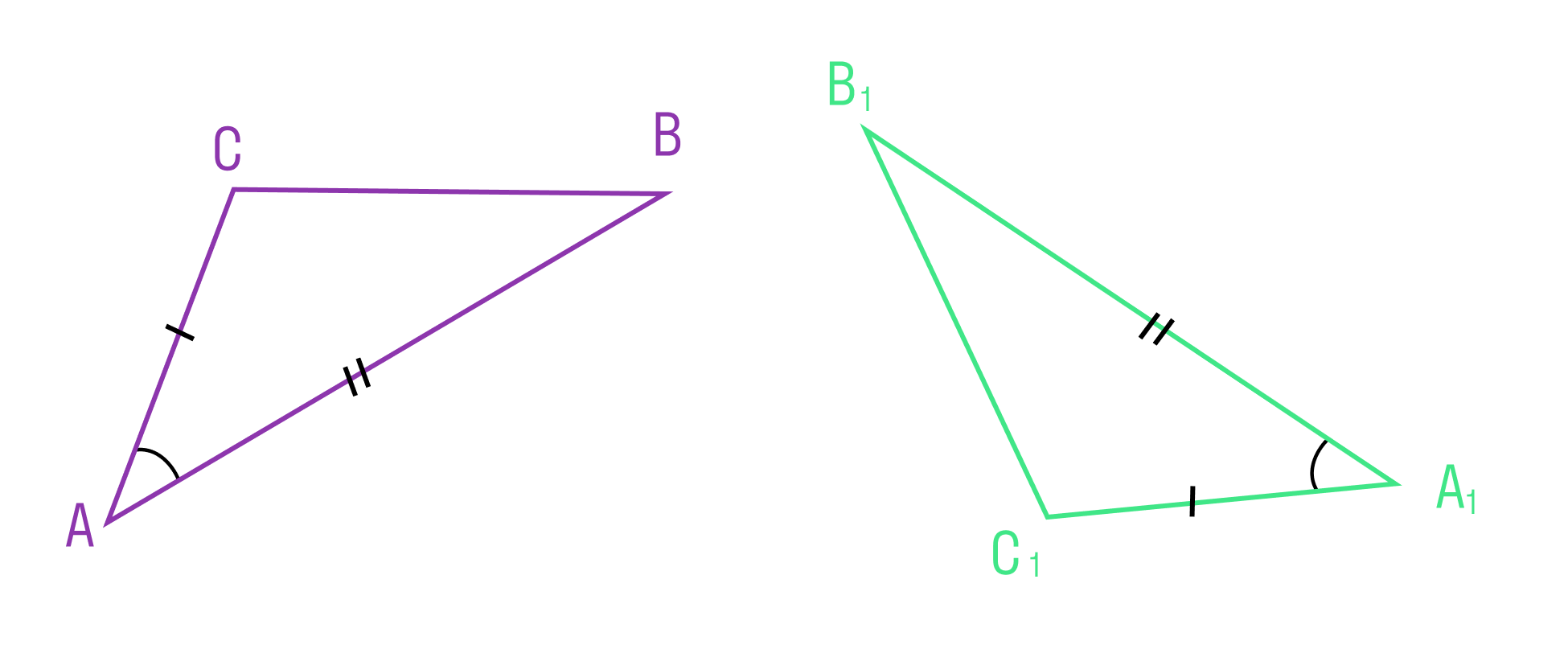
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны
Второй признак равенства треугольников
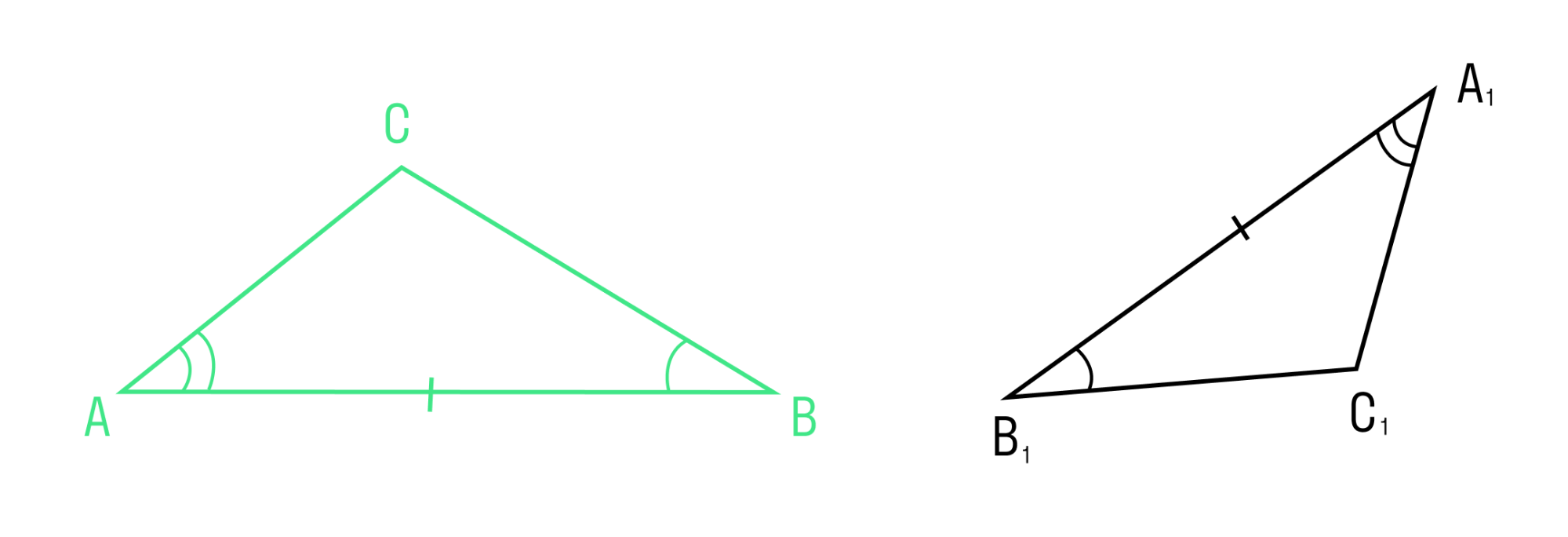
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Третий признак равенства треугольников
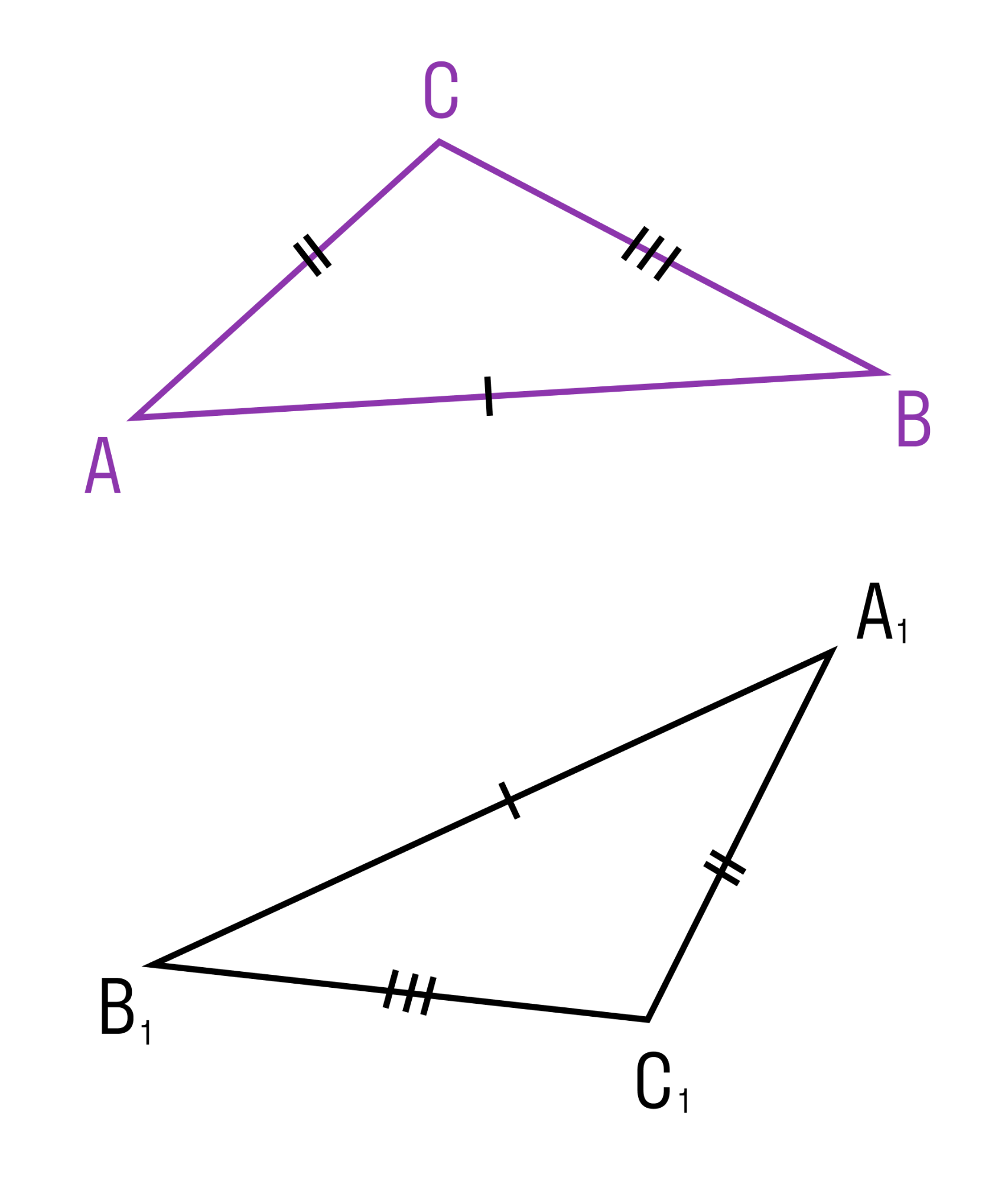
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Из теоремы следует, что треугольник — жесткая фигура, то есть фигура, которую невозможно деформировать.
Подобные треугольники
Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника пропорциональны сходственным сторонам другого треугольника.
Треугольники АВС и A1B1C1 будут подобны, если
Число k, которое равно отношению сходственных сторон подобных треугольников, называется коэффициентом подобия.
Подобие треугольников обозначают специальным символом — ∾. На рисунке треугольники АВС и A1B1C1 подобны, это можно записать так: ΔАВС ∾ ΔA1B1C1.
Теорема о первом признаке подобия треугольников
Если два угла одного треугольника соответственно равны двум углам другого, то такое треугольники подобны.
Второй признак подобия треугольников
Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника и углы, заключенные между этими сторонами, равны — такие треугольники подобны.
Третий признак подобия треугольников
Если три стороны одного треугольника пропорциональны трем сторонам другого, то такие треугольники подобны.
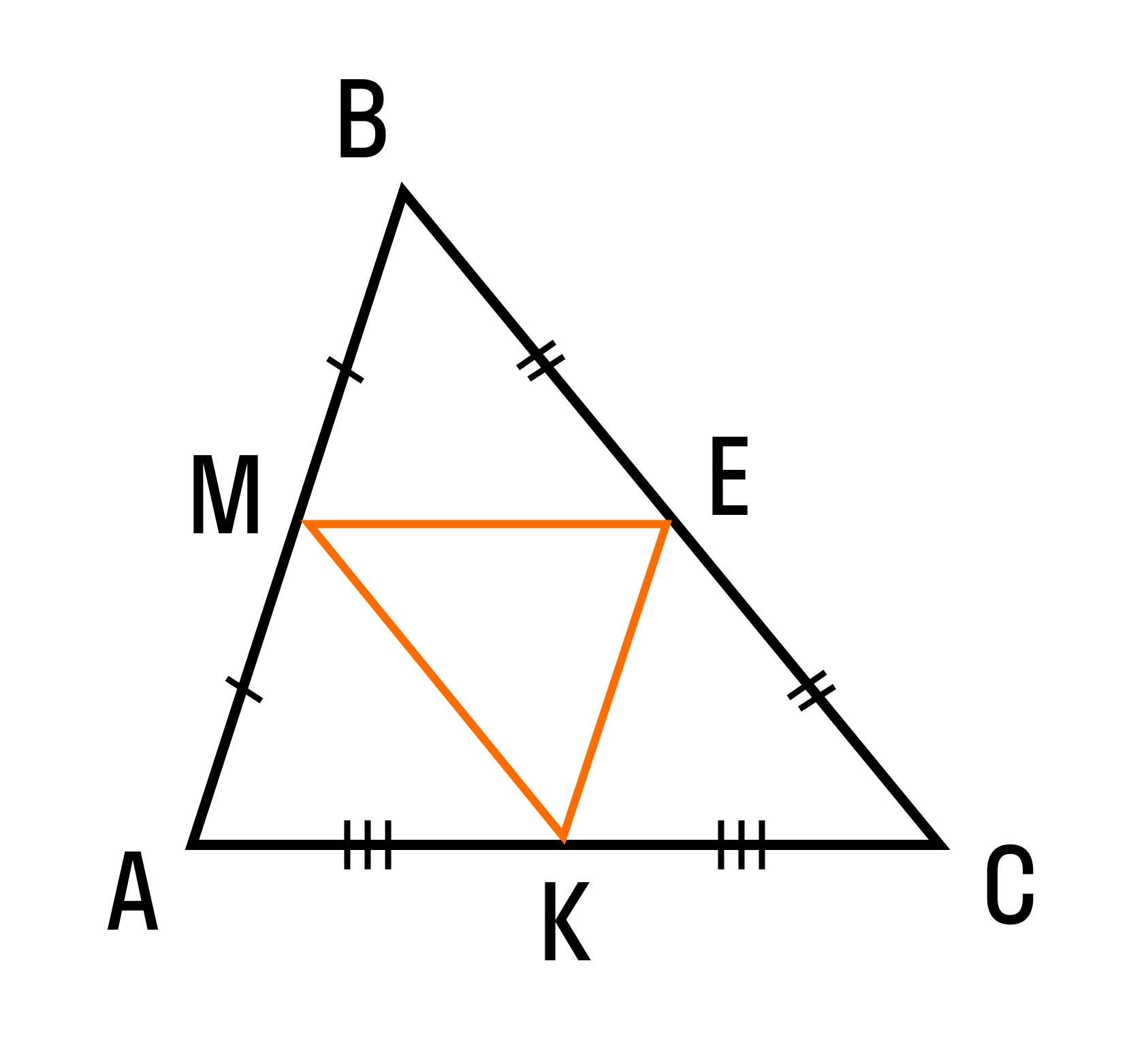
Средняя линия треугольника — это отрезок, который соединяет середины двух его сторон. В каждом треугольнике можно провести три средних линии, при пересечении которых получается четыре равных треугольника, подобных исходному с коэффициентом подобия 1/2.
На рисунке изображен треугольник АВС. Отрезки МЕ, МК и КЕ — средние линии данного треугольника, ΔВМЕ = ΔАМК = ΔСЕК = ΔМЕК.
Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.
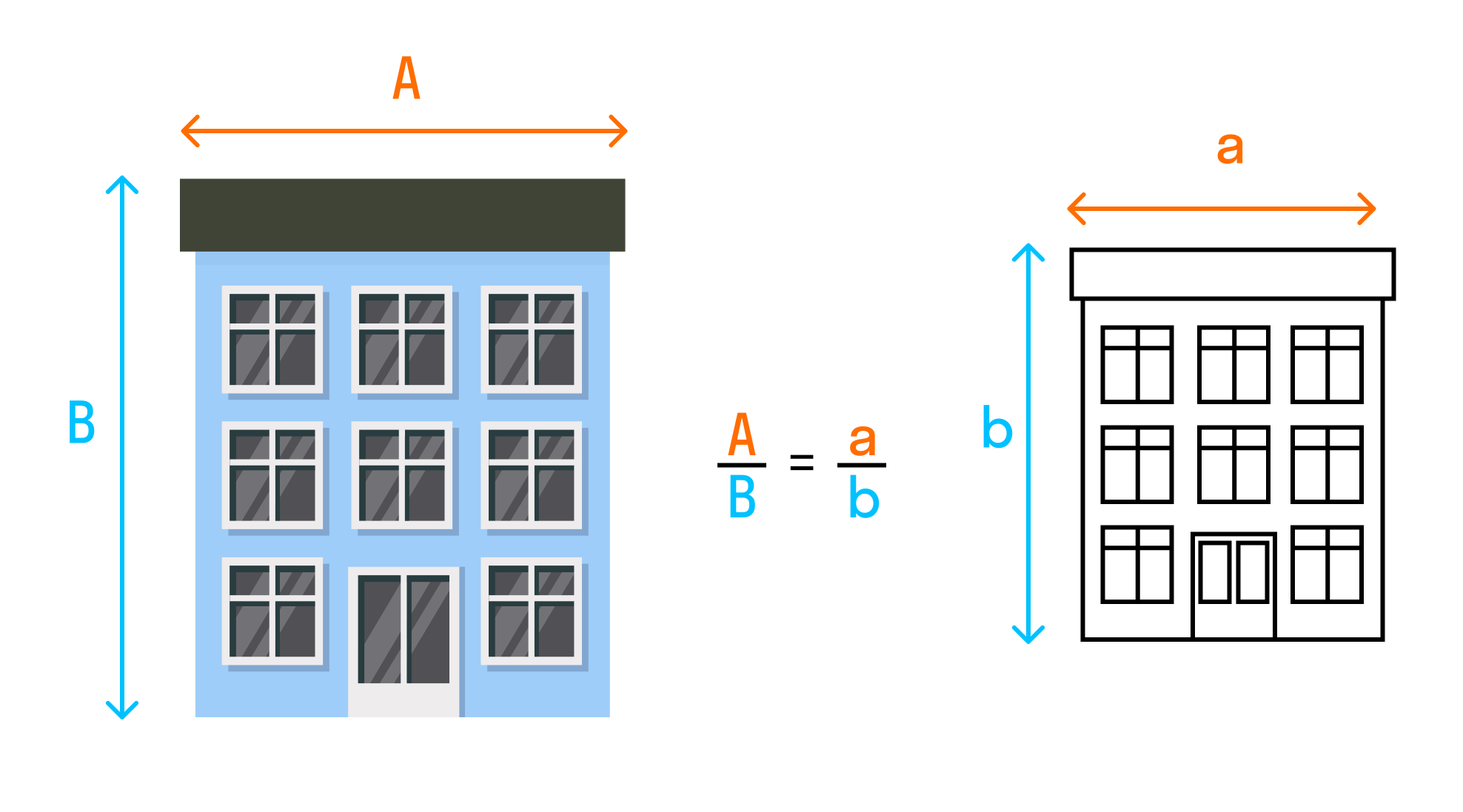
Важно понимать, что подобие в математике — это то, что в обычной жизни мы называем схожестью. Нарисовали треугольники или прямоугольники и говорим, что они похожи потому, что их стороны пропорциональны.
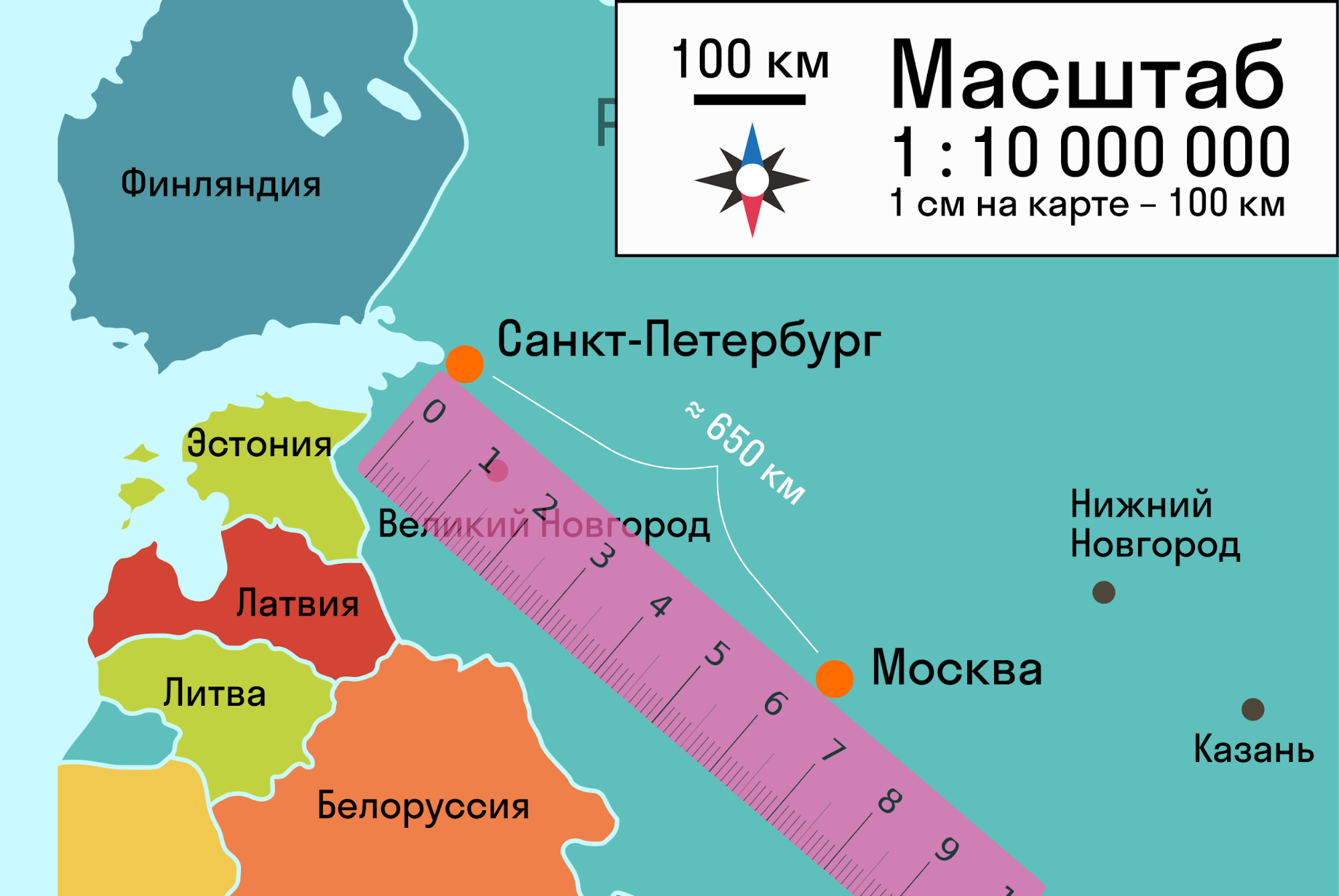
Пример подобия — карта. Она подобна местности, которую отражает. А масштаб — это и есть коэффициент подобия. С треугольниками или другими фигурами точно также.
Классификация треугольников по их сторонам
Для классификации треугольников можно использовать их типологию.
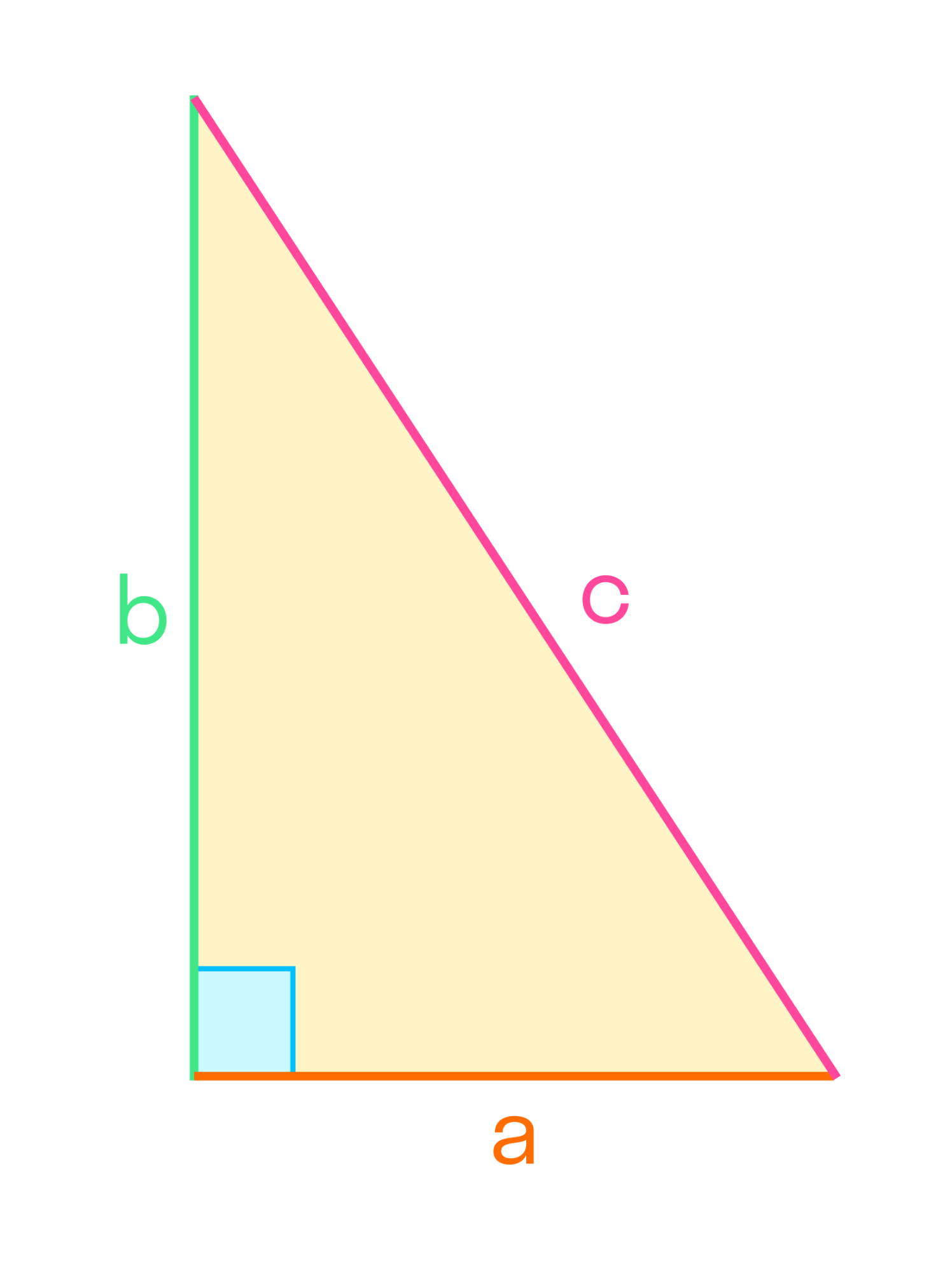
Один из распространенных типов — прямоугольный треугольник. Если один из углов прямой, то это накладывает определенные свойства на треугольник. Прямоугольный треугольник — это также половина прямоугольника.
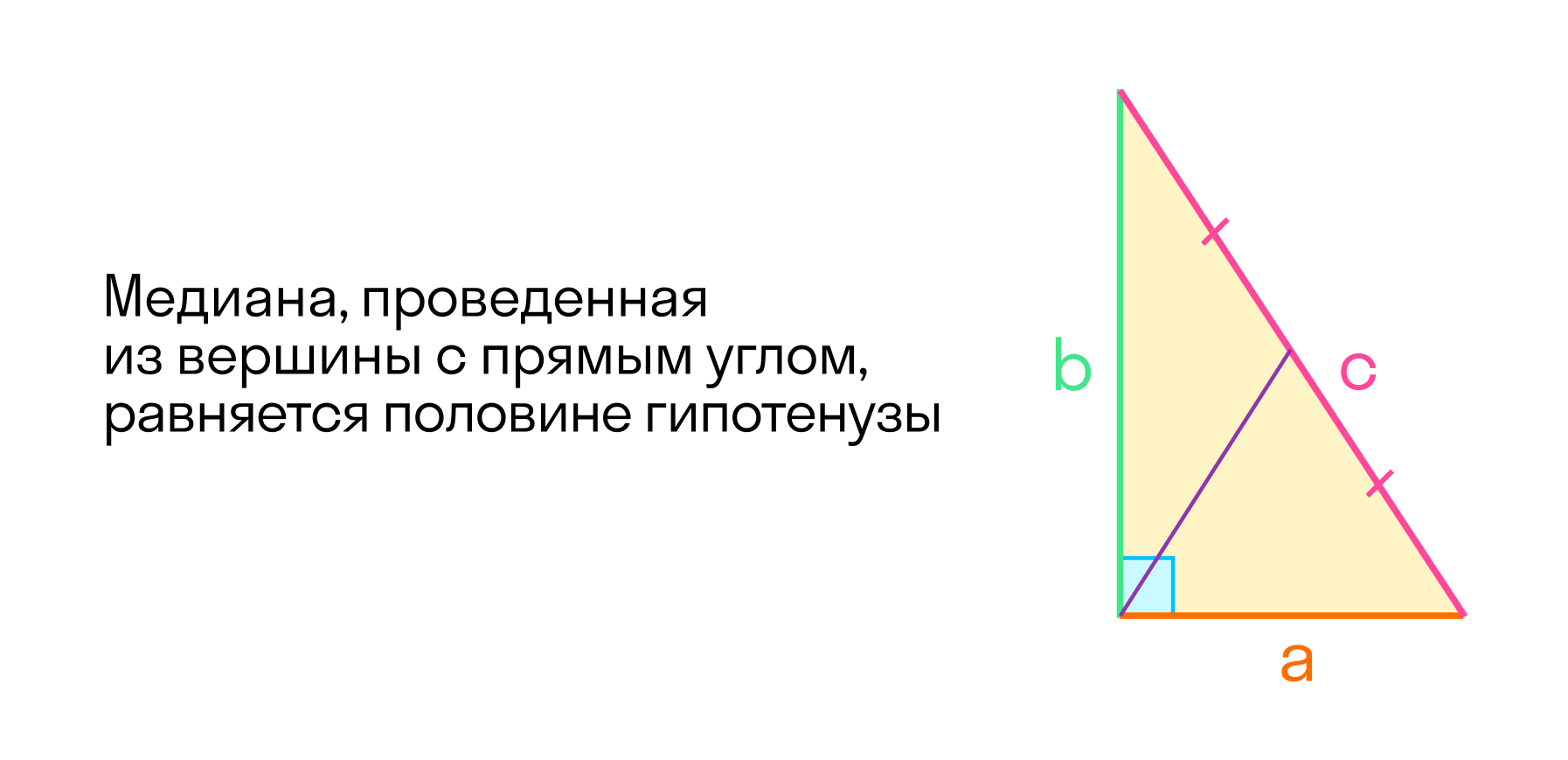
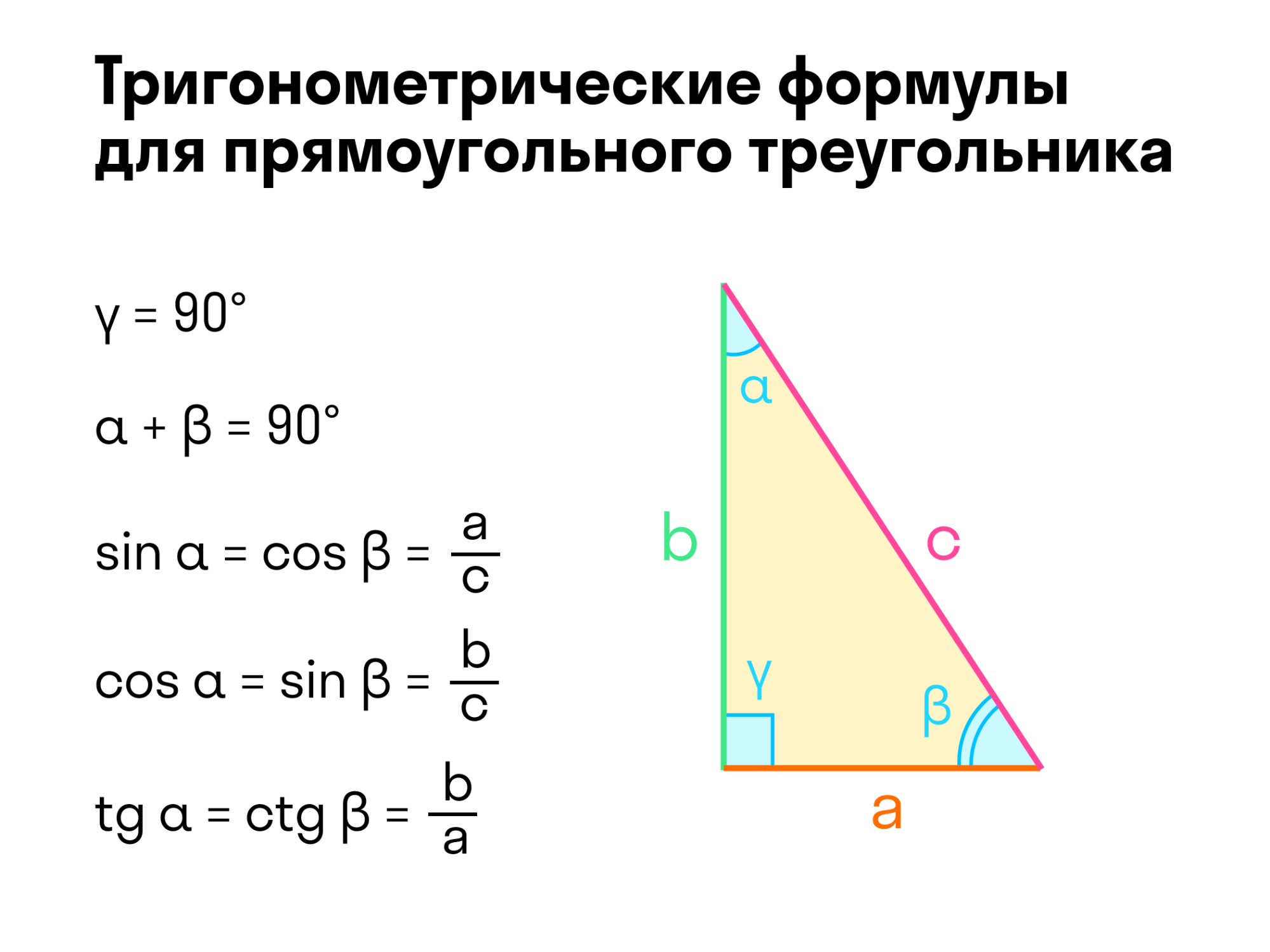
Свойства прямоугольного треугольника
С прямоугольных треугольников начинается изучение тригонометрии. Можно измерять углы с помощью отношений, использовать понятия синуса, косинуса. Помним, что угол можно задать двумя числами, их отношением.
Если две стороны треугольника равны, то это равнобедренный треугольник — и тогда у него есть ось симметрии. Если нарисовать такой треугольник и сложить лист пополам, то две части треугольника совпадут. Эта особенность дает треугольнику определенные свойства.
Симметричный треугольник, у которого все углы и стороны равны — это равносторонний треугольник. У таких треугольников три оси симметрии. Это значит, что если мы повернем треугольник на 60 градусов, то получим точно такой же треугольник.
Такой треугольник задается одним параметром — длиной стороны. Она полностью определяет все другие значения и размеры в этом треугольнике.
От правильного треугольника может плавно перейти к правильным многоугольникам. У треугольника 3 угла, у четырехугольника — 4, а у пятиугольника — 5 углов. У многоугольника много углов🙃
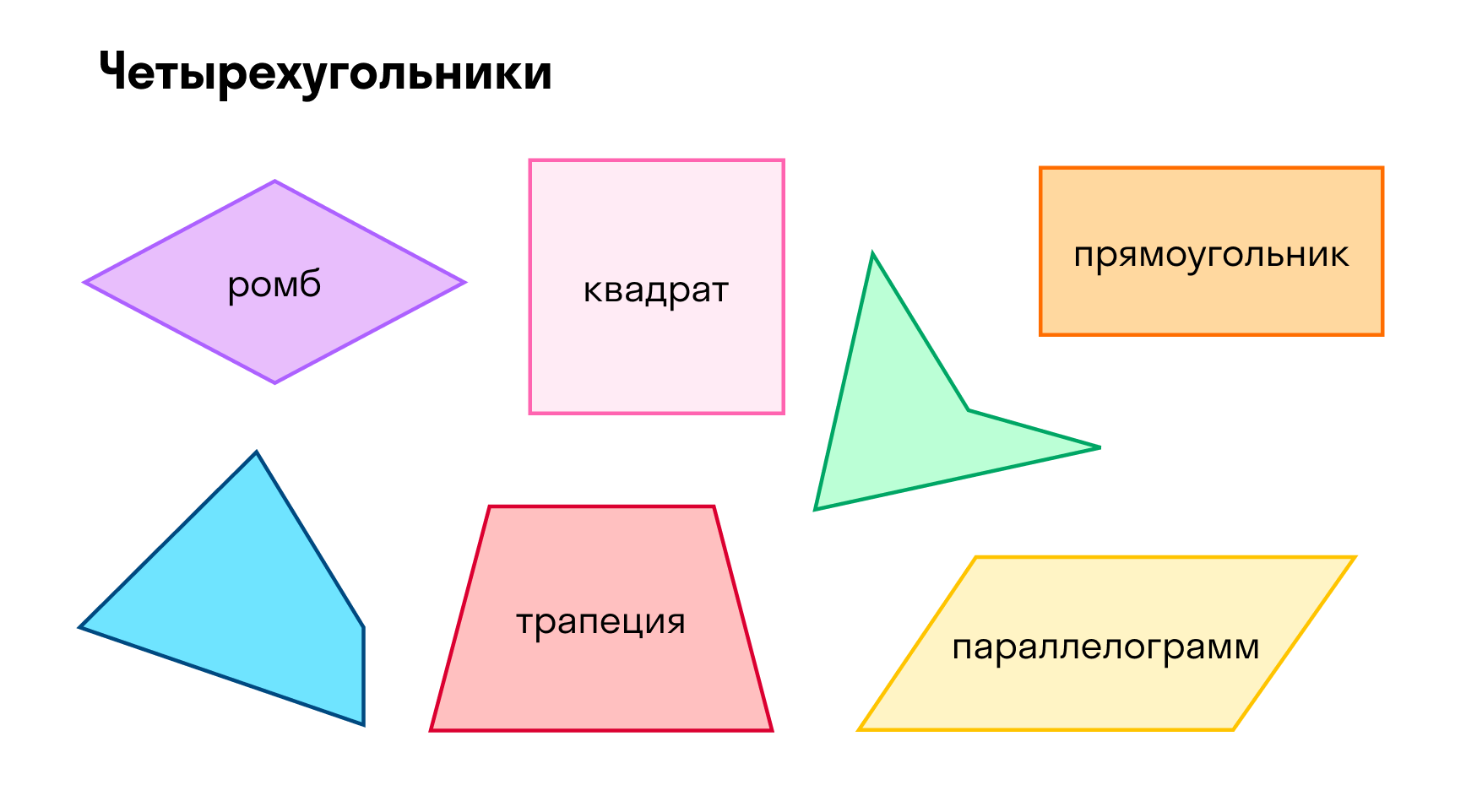
Четырехугольники
Про четырехугольники мы много говорим на уроках в школе: прямоугольник, квадрат, ромб.
Но говорим о них не в общем случае, как для треугольников (такие вещи, как теорема синусов, косинусов), а можем формулировать только какие-то свойства для определенных видов четырехугольников.
Четырехугольникам лучше уделить побольше времени — у каждого из них есть особые свойства, которые не пригодятся для других фигур. Поэтому каждый четырехугольник лучше внимательно изучить на уроке или почитать в наших материалах:
Окружность
Окружность — это еще один объект, который полезно изучить. Ее легко описать, она задается одним параметром — радиусом. А еще часто встречается в физике и в обычной жизни. Например, когда капля падает в воду, от нее остаются следы — маленткие окружности.
Взаимодействие объектов
Следующий уровень — это взаимодействие всех-всех объектов, о которых мы говорили раньше.
Например, окружность и прямая. Прямая может находиться где-то в стороне от окружности, может ее пересекать, а может касаться, то есть пересекать в одной точке.
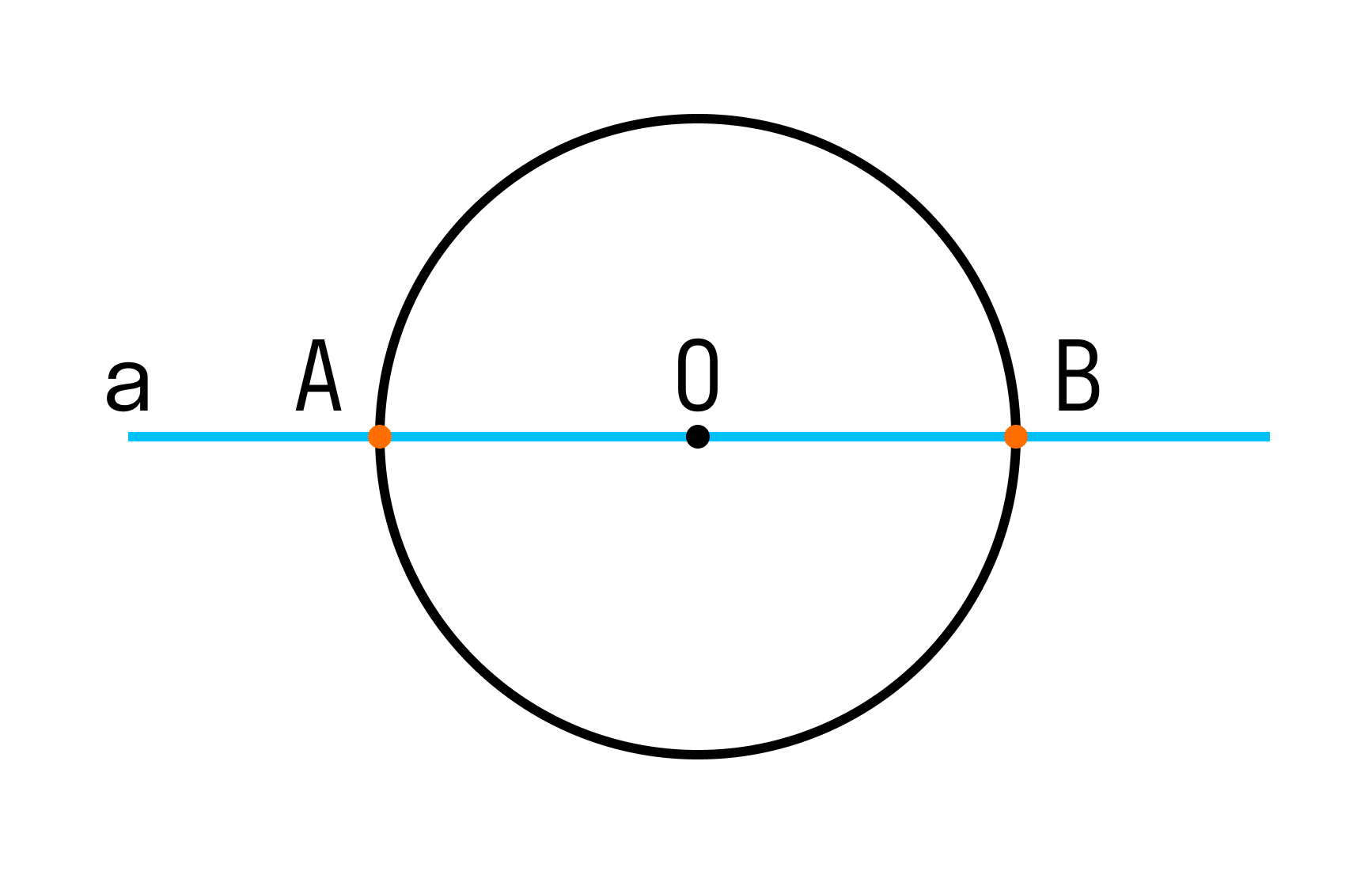
Если прямая проходит через центр окружности, то она пересекает окружность в двух точках — концах диаметра, который лежит на на этой прямой.
На рисунке прямая a проходит через центр окружности (точку О) и пересекает ее в двух точках А и В, которые являются концами диаметра АВ данной окружности.
Если прямая a не проходит через центр О окружности радиуса r, то возможны три случая взаимного расположения прямой и окружности — в зависимости от соотношения между радиусом r этой окружности и расстоянием d от центра окружности до прямой a. Вот эти случаи:
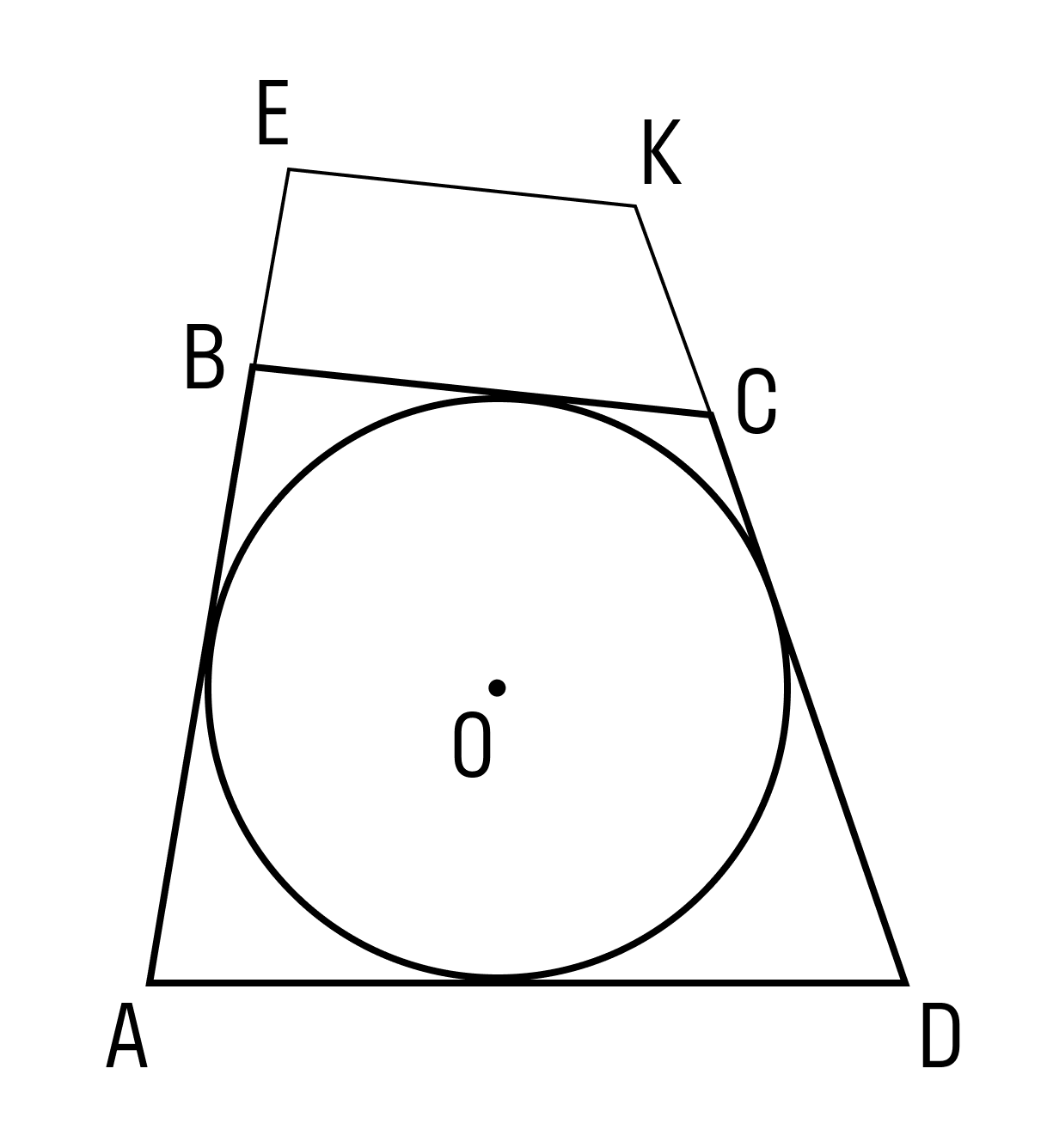
Окружность вписанная в многоугольник — это окружность, которая касается всех сторон многоугольника. Центр вписанной окружности лежит внутри многоугольника, в который она вписана. Описанный около окружности многоугольник — это многоугольник, в который вписана окружность.
На рисунке четырехугольник АВСD описан около окружности с центром О, а четырехугольник АЕКD не является описанным около этой окружности, так как сторона ЕК не касается окружности.
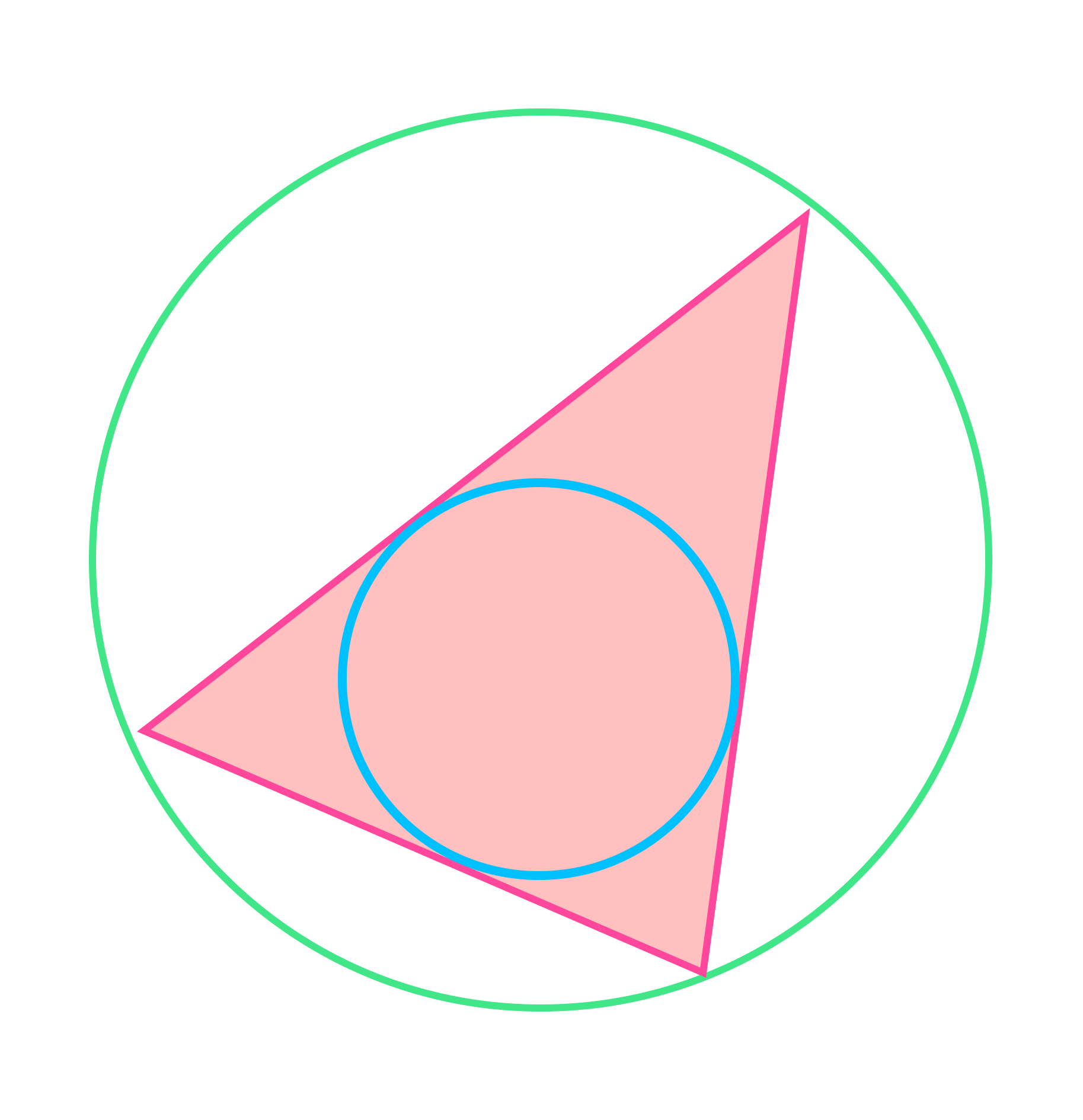
В любой треугольник можно вписать только одну окружность, и вокруг любого ее можно описать.
Все это верно только для треугольников. Не в любой четырехугольник можно вписать окружность, и не вокруг любого можно описать. Более подробно эту тему можно изучить на уроках математики: признаки, теоремы и правила.
Практическая сторона геометрии
Название «геометрия» переводится с греческого, как «гео» — земля и «метрео» — мерить. Изначально геометрию использовали для разметки земли и других работ с землей. Но, оказалось, что сфера ее влияния безгранична.
Чтобы понять, зачем нам нужны знания по геометрии, просто оглянитесь вокруг: геометрия окружает нас в предметах разных форм. Взять хотя бы круг: его используют в искусстве, строительстве, технике. То же самое и с другими фигурами: чтобы сконструировать автомобиль или айфон, сшить одежду или построить дом — не обойтись без геометрии.
А еще геометрия помогает научиться рассуждать логически, искать связи и противоречия — полезный навык в диджитал-мире, когда информация окружает нас повсюду.
Вот, в каких профессиях пригодится геометрия: архитектор, айтишник, дизайнер, инженер, конструктор, строитель, smm-менеджер, декоратор, летчик, водитель, художник, проектировщик, астроном, спортсмен, музыкант и другие.
Почему изучать геометрию просто: мы видим объемный мир каждый день и регулярно прикасаемся к предметам, строим планы, размышляем и считаем в уме. В геометрии все знания подкреплены научными теориями — это помогает взаимодействовать с пространством по-другому, более осознанно.
Почему изучать геометрию сложно: некоторые правила придется учить наизусть.
Чтобы понять геометрию, двигайтесь от простого к сложному. Многие теоремы могут показаться очевидными. Но эта видимость может быть верной только для одного рисунка. Невозможно нарисовать все ситуации, ведь их их бесконечное множество. Именно поэтому важно доказать истину, чтобы никогда не сомневаться в ней.
Чему равен R в геометрии?
Что означает буква R в геометрии?
В математике: R — в математике: обозначение множества всех вещественных чисел. R или r — в геометрии: обозначение радиуса.
Как найти R маленькую в геометрии?
R = S : p, где S — площадь треугольника, p — полупериметр треугольника.
Что такое A в геометрии?
Для обозначения геометрических фигур и их проекций, для отображения отношения между геометрическими фигурами, а также для краткости записей геометрических предложений, алгоритмов решения задач и доказательства теорем используются символьные обозначения. … А`≡ В` – горизонтальные проекции точек А и В совпадают.
Как найти C в геометрии?
Чем R отличается от R в геометрии?
Чем отличается r от R (в геометрии)?
Двумя этими буквами в геометрии обычно обозначается радиус окружности. маленькая r — радиус вписанной в фигуру окружности (окружность внутри фигуры); большая R — радиус описанной около фигуры окружности (фигура внутри окружности).
Что обозначается буквой R?
латинская буква R в окружности — ® словесное обозначение «товарный знак» словесное обозначение «зарегистрированный товарный знак»
Как найти длину круга?
Каким значком обозначается пересечение в геометрии?
Теория множеств и теория чисел
| Символ TeX (Команда TeX) | Символ (Юникод) | Название |
|---|---|---|
| Произношение | ||
| (cap) | ⋂ | Пересечение |
| «Пересечение … и …», «…, пересечённое с …» | ||
| (setminus) | Разность множеств |
Как обозначается в геометрии?
А. Обозначение геометрических фигур
| № по пор. | Обозначение | Пример символической записи |
|---|---|---|
| 1 | ≡ | (АВ)≡(CD) — прямая, проходящая через точки А и В, совпадает с прямой, проходящей через точки С и D |
| 2 | ≅ | ∠ABC≅∠MNK — угол АВС конгруентен углу MNK |
| 3 | ∼ | ΔАВС∼ΔMNK — треугольники АВС и MNK подобны |
| 4 | || | α||β — плоскость α параллельна плоскости β |
Что значит две полоски в геометрии?
Тильда используется и в сочетании с другими знаками: тильда над знаком равенства в геометрии обозначает конгруэнтность; две тильды (≈) — приближённое равенство; тильда под знаками «больше» и «меньше» означает, что одна функция растёт асимптотически не меньше (не больше) другой и т. п.
Как найти длину окружности зная площадь?
Формула вычисления площади круга
Как найти с в математике?
В 4 классе ученики решают много задач по математике с примением формулы нахождения скорости, времени или расстояния при равномерном движении. Эта формула выглядит так: S = V×t. В данной формуле S — это путь, V — скорость, а t — время.
Как найти H в геометрии?
h = 2/a √p(p-a)(p-b)(p-c), где h — длина высоты треугольника, p — полупериметр, a — длина стороны, на которую падает высота (основание), b и c — длины двух других сторон треугольника.
19 метрик, которые играют решающую роль в социальных сетях
Что такое метрики социальных сетей? И почему специалисту по социальным сетям важно уметь их измерять и интерпретировать? В первую очередь, это шанс продемонстрировать и доказать ценность проделанной работы и результат принятых решений.
Если ваш начальник попросит обсудить с ним данные, воспользуйтесь возможностью выглядеть профессионалом и выходите за рамки поверхностных, «тщеславных» метрик ー лайков, репостов и ретвитов. Вместо этого сосредоточьтесь на данных, которые действительно важны ー цифрах, доказывающих, что ваши усилия как маркетолога положительно повлияли на бизнес.
Объективные данные убедят руководителей в том, что их инвестиции в социальные сети окупаются. Цифры также помогут вам в будущем продолжать принимать более разумные решения.
В этой статье рассматриваются метрики социальных сетей, которые действительно имеют большое значение. Мы поговорим о том, почему они важны и как их отслеживать.
Готовы произвести впечатление на босса?
Оглавление
Социальная воронка: распределение
Социальная воронка: распределение
Прежде чем углубляться, давайте рассмотрим, где каждая из метрик располагается в социальной воронке.
Мы разделим воронку на четыре ключевых этапа, через которые проходит пользователь:
На каждом этапе присутствует собственный набор обязательных для измерения показателей, KPI, которые проливают свет на эффективность маркетинга в социальных сетях.
Метрики узнавания
Эти цифры объясняют, кто ваша текущая и потенциальная аудитория.
Узнаваемость бренда
Узнаваемость бренда ー это внимание аудитории, которое ваш бренд получает во всех социальных сетях в течение отчётного периода или определённого времени, за которое можно собрать статистически значимые данные.
Интерес аудитории можно измерить с помощью различных показателей социальных сетей, в том числе количества @упоминаний, репостов, ссылок на посты и показов. Периоды отчётности также можно изменять. Обычно они длятся неделю, месяц или квартал.
Коэффициент роста аудитории
Коэффициент роста аудитории измеряет скорость, с которой увеличивается число подписчиков вашего бренда в социальных сетях. То есть насколько быстро вы набираете подписчиков.
Поскольку во всём мире доступ к интернету всё легче получить, в социальных сетях число подписчиков компаний-брендов также будет увеличиваться.
Примечание: таким же образом вы можете отслеживать прогресс ваших конкурентов.
Охват поста
Охват поста обозначает, сколько людей увидели пост с момента его публикации.
Этот показатель легко найти и ещё проще интерпретировать. Самое главное, на него можно повлиять, поскольку охват зависит от времени выхода поста (т.е. когда ваша аудитория онлайн) и содержание материала (т.е. что ваша аудитория считает ценным в посте).
ШАГ 1. Измерьте охват любого поста.
ШАГ 2. Чтобы получить процент охвата поста, разделите охват на общее число подписчиков и умножьте на 100.
Примечание. На Facebook функция «Когда ваши подписчики онлайн» покажет вам оптимальное время для публикации. Используйте эти данные, чтобы увеличить охват.
На рис. Когда ваши подписчики онлайн. Данные отображаются за последнюю неделю. Время суток показано для зоны тихоокеанского времени.
Потенциальный охват
Потенциальный охват измеряет количество людей, которые действительно могут увидеть сообщение в течение отчётного периода.
Другими словами, если один из подписчиков сделает репост вашей публикации у себя в аккаунте, примерно от 2% до 5% его подписчиков будут составлять потенциальную аудиторию этого поста.
Понимание этого показателя важно, потому что как SMM-маркетолог, вы всегда должны работать над расширением аудитории. Зная потенциальный охват, вы сможете оценить прогресс.
Потенциальный охват составляет от 2% до 5% теоретического охвата.
Доля голоса в соц сетях (SSoV)
Доля голоса в соц сетях показывает, сколько людей упоминают ваш бренд в социальных сетях по сравнению с вашими конкурентами.
Упоминания могут быть:
Метрики вовлечения
Эти цифры показывают, как люди взаимодействуют с вашим контентом.
Степень одобрения
Степень одобрения ー это количество действий по одобрению (например, лайков, сохранений в избранном), которые получает публикация относительно общего числа подписчиков.
Когда подписчик ставит лайк или сохраняет в избранные ваш пост, он признаёт, что информация ценна для него. Знание того, какой процент вашей аудитории признаёт ценными ваши посты, может и должно влиять на создание вашего будущего контента.
Примечание. Используйте инструмент воздействия на социальные сети, чтобы отслеживать действия по одобрению и упростить процесс.
Средний уровень вовлечённости
Средний уровень вовлечённости ー это количество действий, указывающих на вовлечение в контент (например, лайки, репосты, комментарии) относительно общего количества подписчиков.
Это важный показатель, потому что более высокая вовлечённость означает, что ваш контент резонирует с аудиторией. Чтобы доказать это, отследите уровень вовлечённости каждого поста. Если у вас высокий уровень вовлечённости, фактическое количество лайков, репостов и комментариев не имеет значения.
Примечание. Оценка этого показателя отличается на каждой платформе.
Например, Facebook и Twitter обычно имеют более низкий уровень вовлечённости (например, от 0,5% до 1%). Instagram, с другой стороны, известен своими относительно высокими показателями вовлечённости (например, от 3% до 6%).
Коэффициент распространения
Коэффициент распространения ー это отношение количества репостов публикации к общему количеству подписчиков.
Термин придумал Авинаш Кошик, автор и евангелист цифрового маркетинга в Google. Распространение ー «скорость, с которой ваши подписчики берут ваш контент и делятся им со своими подписчиками».
По сути, чем выше коэффициент распространения, тем больше желание ваших подписчиков ассоциировать себя с вашим брендом.
Показатель вирусности ー это количество людей, которые поделились вашим постом, относительно количества уникальных просмотров (т. е. показов) за отчётный период.
Как и другие показатели в этом списке, показатель вирусности не лежит на поверхности. Он означает больше, чем просто лайки. «Пост, который получает 17 000 лайков, может получить только 0,1% вирусности, ー пишет Николас Гремион, ー в то время как другой пост, который получает 10 000 лайков, получает 9,97% вирусности ー и это намного лучше».
Метрики конверсии
Эти цифры демонстрируют эффективность вовлечённости в соцсетях.
Коэффициент конверсии
Коэффициент конверсии ー это число посетителей, которые после нажатия на ссылку в вашем посте предпринимают действия на странице (например, подписываются на рассылку новостей, скачивают контент с ограниченным доступом, регистрируются на вебинар) относительно общего количества посетителей этой страницы.
Высокий коэффициент конверсии означает, что ваш контент является ценным и привлекательным для целевой аудитории. С точки зрения социальных сетей, это признак того, что ваш пост был релевантен предложению. Другими словами, он сдержал своё обещание.
Примечание. Коэффициент конверсии поста может быть высоким, даже если трафик низкий. Две метрики являются взаимоисключающими.
Показатель кликабельности (CTR)
Показатель кликабельности (CTR) ー говорит о том, как часто люди нажимают на ссылку с призывом к действию в вашей публикации.
Чтобы не смешивать его с другими действиями по вовлечению (например, репост, лайк, комментарий), CTR специально связан со ссылкой, которая ведёт аудиторию на дополнительный контент.
Частое и точное отслеживание CTR даст вам бесценное представление о том, насколько привлекательно ваше предложение для целевой аудитории.
Примечание. Не забывайте измерять клики и показы за один и тот же отчётный период.
Показатель отказов
Показатель отказов ー это процент посетителей страницы, которые нажимают на ссылку в вашем сообщении и быстро покидают целевую страницу без каких-либо действий.
Показатель отказов позволяет измерить ваш трафик в социальных сетях и рентабельность инвестиций ROI в сравнении с другими источниками трафика (например, трафик с поста Facebook против трафика из органической выдачи Google).
Если показатель отказов для людей, пришедших из социальных сетей, ниже, чем для трафика из других источников, это свидетельствует о том, что ваши кампании в социальных сетях нацелены на нужную аудиторию и, в свою очередь, стимулируют высокий трафик.
Цена за клик
Цена за клик ー это сумма, которую вы платите за каждый клик по рекламному сообщению в социальных сетях.
Выбираете ли вы рекламу в Facebook, Instagram, Twitter или LinkedIn, не думайте об общих расходах. Вместо этого посмотрите на цену за клик. Это поможет вам оценить, выгодны ли ваши инвестиции в привлечение внимания аудитории или не выгодны.
Примечание. Никогда не позволяйте кампаниям с ценой за клик оставаться без присмотра в течение длительного периода времени.
Стоимость тысячи показов или CPM
Стоимость тысячи показов или CPM ー это сумма, которую вы платите каждый раз, когда тысяча человек прокручивает ваш пост в социальных сетях.
В отличие от кампании с ценой за клик, публикация с ценой за тысячу показов необязательно побуждает людей к действию. Она только создаст показы, просмотры. Следовательно, CPM ー это более быстрый и менее дорогой способ провести сплит-тест.
ШАГ 1. Зайдите в Менеджер рекламных объявлений на вашей платформе.
Примечание. Никогда не позволяйте кампаниям CPM оставаться без присмотра в течение длительного периода времени.
Коэффициент конверсии в социальных сетях
Коэффициент конверсии в социальных сетях ー это общее количество конверсий из социальных сетей, выраженное в процентах.
Показатель обсуждения
Показатель обсуждения ー это отношение количества комментариев под публикацией к общему количеству подписчиков.
Это ещё одна метрика, придуманная Авинашем Каушиком. И она лучше, чем отслеживание комментариев без какого-либо контекста. В конце концов, получение в среднем 20 комментариев на пост намного более впечатляюще, если у вас только 200 подписчиков.
Отслеживание показателя обсуждения поможет вам понять, какая часть аудитории хочет добавить свой голос в контент, который вы публикуете в социальных сетях. Или, как говорит Каушик: «То, что вы пишете, достаточно интересно, чтобы зажечь самое социальное из всего ー разговор?»
Метрики клиентов
Эти цифры показывают, что ваши активные клиенты думают и как относятся к вашему бренду.
Отзывы клиентов
Отзывы клиентов ー это любые отзывы, оценки, комментарии, поддержка или интервью клиентов, касающиеся бренда.
В конечном счёте отличные отзывы являются результатом восхищения клиентов. Если ваш бренд делает людей счастливыми, они с большей вероятностью поделятся своим опытом с другими.
Преимущества очевидны: непрерывный поток искренних отзывов в социальных сетях заслужит доверие и авторитет, одновременно усиливая присутствие вашего бренда.
Хотите больше отзывов клиентов?
Степень удовлетворённости клиентов (CSAT)
Степень удовлетворённости клиентов или CSAT ー это метрика, показывающая, насколько люди довольны вашим продуктом или услугой.
Обычно оценка CSAT является ответом на один простой вопрос: насколько полно этот продукт удовлетворяет ваши потребности?
Затем клиентов просят оценить удовлетворённость продуктом по линейной шкале, численно (например, от 1 до 10) или эмоционально (например, плохо, удовлетворительно, хорошо, отлично, превосходно).
Показатель CSAT стал почти повсеместным способом понять, как клиенты относятся к бренду, главным образом потому, что он понятен, лаконичен и прост в управлении, особенно в социальных сетях.
Net Promoter Score (NPS)
Net Promoter Score (NPS) ー это показатель, который измеряет лояльность клиентов.
В отличие от CSAT, NPS хорошо предсказывает будущее взаимодействие с клиентами, поскольку этот показатель является ответом на один конкретно сформулированный вопрос: насколько вероятно, что вы порекомендуете нашу [компанию / продукт / услугу] другу?
Затем клиентов просят ответить по шкале от 0 до 10. На основании ответа каждый клиент заносится в одну из трёх категорий:
NPS уникален тем, что он измеряет удовлетворенность клиентов, а также будущие продажи. Это делает его ценным, необходимым показателем для компаний всех размеров.
«Да, конечно», ー говорите вы, ー я бы хотел поговорить о данных».
Независимо от того, встречаетесь ли вы с начальником раз в месяц или раз в день, ваши разговоры о данных будут более содержательными и результативными, если вы выделите метрики социальных сетей, которые демонстрируют эффект ваших усилий.
Так что копайте глубже и выходите за рамки легкодоступных “показателей тщеславия”, о которых может сообщить буквально каждый. Продемонстрируйте свои навыки, представив аналитику в социальных сетях, рассказывающую историю. Рассказ, который по своей сути полезен для вашей организации.
Придется уделить работе больше времени, но взамен вы получите несравнимо больше!
Перевела Татьяна Пушкина специально для Сonvert Monster. Использовать материал разрешено только с активной ссылкой на перевод.
Подпишись и следи за выходом новых статей в нашем монстрограмме
Остались вопросы?
Не нашли ответ на интересующий Вас вопрос? Или не нашли интересующую Вас статью? Задавайте вопросы и темы статей которые Вас интересуют в комментариях.