Что значит сместиться на вектор в чертежнике
§ 18. Управление исполнителем Чертёжник
Знакомимся с Чертёжником
Исполнитель Чертёжник предназначен для построения рисунков на координатной плоскости.
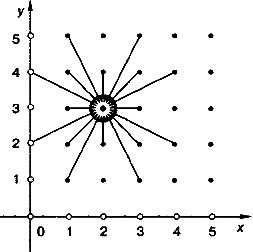
При задании точек этой координатной плоскости, в отличие от того, как это принято в математике, координаты хну разделяются запятой. Например, координаты выделенной на рис. 63 точки будут записаны так: (1, 1).
Чертёжник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остаётся след — отрезок от предыдущего положения пера до нового. При перемещении поднятого пера никакого следа на плоскости не остаётся. В начальном положении перо Чертёжника всегда поднято и находится в точке (0, 0).
По команде поднять перо Чертёжник поднимает перо. Если перо уже было поднято, Чертёжник игнорирует эту команду: он не меняет положение пера и не сообщает об отказе. Иначе говоря, каким бы ни было положение пера до команды поднять перо, после этой команды оно будет поднятым.
Точно так же, независимо от первоначального положения, после выполнения команды опустить перо оно оказывается опущенным, т. е. готовым к рисованию.
Рисунки Чертёжник выполняет с помощью команд сместиться в точку и сдвинуться на вектор.
По команде сместиться в точку (а, b) Чертёжник сдвигается в точку с координатами (а, b). На рисунке 64 показаны результаты выполнения команды сместиться в точку (2, 3) при различных положениях пера до этой команды. Видно, что, независимо от предыдущего положения, перо оказывается в точке (2, 3), но длина и направление отрезка, который при этом чертится, могут быть различны. Команду сместиться в точку называют командой абсолютного смещения.
Назовите координаты точек, в которых находился Чертёжник до выполнения команды сместиться в точку (2, 3) (см. рис. 64).
В каком случае в результате выполнения команды сместиться в точку (2, 3) из некотрого показанного на рис. 64 начального положения не будет прочерчен ни один отрезок?
Пусть перо Чертёжника находится в точке (x, у). По команде сместиться на вектор (а, b) Чертёжник отсчитывает а единиц вправо вдоль горизонтальной оси (оси абсцисс), b единиц вверх вдоль вертикальной оси (оси ординат) и сдвигает перо в точку с координатами (х + а; у + b). Таким образом, координаты, указанные в команде, отсчитываются не от начала координат, а относительно текущего положения пера Чертежника. Поэтому команду сместиться на вектор называют командой относительного смещения.
На рисунке 65 показаны результаты выполнения команды сместиться на вектор (2, 3) при различных положениях пера до этой команды. Из рисунка видно, что положение пера после этой команды зависит от его предыдущего положения, зато в результате получаются отрезки, длина и направление которых одинаковы.
В математике направленные отрезки называются векторами, отсюда и происходит название команды.
Назовите координаты точек, в которых находилось перо Чертёжника до выполнения команды сместиться на вектор (2, 3) и куда оно переместилось после выполнения этой команды.
Как будет выполняться команда сместиться на вектор (а, b), если:
Служебные слова нц и кц пишутся одно под другим. Чуть правее между ними записывается повторяющаяся последовательность команд (тело цикла). Число повторений — произвольное целое число. Именно столько раз при выполнении алгоритма будут повторены команды, образующие тело цикла.
Предложите вариант решения задачи о почтовом индексе Красноярска с использованием конструкции повторения.
Можно ли обойтись без вспомогательного алгоритма в следующих ситуациях (рис. 72)?
Исполнитель Чертёжник. Пример алгоритма управления Чертёжником
Урок 29. Информатика 6 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Исполнитель Чертёжник. Пример алгоритма управления Чертёжником»
· алгоритм под управлением чертёжника.
На прошлых уроках мы узнали, что существует множество исполнителей и различные формы записи алгоритмов. Для формальных исполнителей алгоритмы записывают в виде программ.
На этом уроке мы познакомимся с исполнителем Чертёжник. С его помощью можно изображать рисунки на координатной плоскости.
Рассмотрим рабочее поле чертёжника.
Рабочим полем чертёжника является декартова система координат, координаты точек, в которой задаются, как и в математической, но разделяются при этом запятой, т.е. точка с координатами (2;3) у чертёжника будет записываться следующим образом.
Если координата точки имеет дробную часть, она отделяется от целой точки. Главным инструментом чертёжника является перо. В начале работы оно находится в точке (0,0), и поднято.
Существует 4 основных команды исполнителя «Чертёжник»:
сместиться в точку;
сместиться на вектор.
Рассмотрим каждую из них.
По команде «опустить перо» цвет пера чертёжника изменится на чёрный. А при перемещении оно начнёт чертить прямую линию от своего предыдущего положения до нынешнего. Если до этого перо было опушено, команда игнорируется.
Есть и противоположная команда.
По команде «поднять перо» перо чертёжника становится белым. И при перемещении перо не оставляет следов. Если до этого перо было поднято – команда игнорируется.
Посмотрим, как выполняются эти команды. Вот что происходит, если опустить перо и переместить его в точку (3,3). Поднять перо и переместить его в точку (6,6).
Так же чертёжник может выполнять 2 команды перемещения
На пример: результатом выполнения команд:
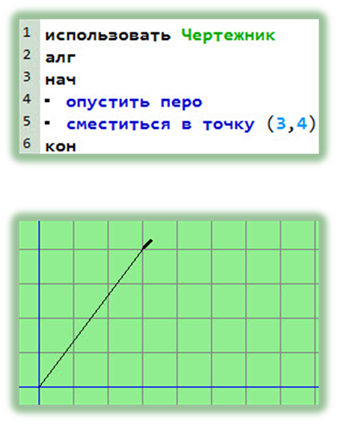
сместиться в точку (3,4)
Будет следующий рисунок.
Ещё одна команда для перемещения: «сместиться на вектор».
Вектор – это отрезок, заданного направления и длины
По этой команде чертёжник перемежается из текущего положения на заданное количество единиц по оси абсцисс и оси ординат. Так, находясь в точке с координатами (x,y) при выполнении команды «Сместиться на вектор (i,j)»
чертёжник переместиться в точку с координатами (x+i, y+j). Данную команду так же называют командой относительного смещения.
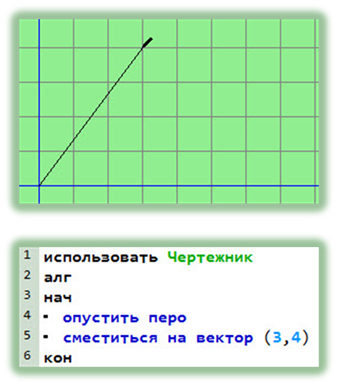
Так уже знакомый нам рисунок можно изобразить, задав другую программу:
сместиться на вектор (3,4)
Чертёжник выполняет только команды, которые записаны правильно.
В ходе написания программы могут быть допущены синтаксические ошибки и логические ошибки.
При логических ошибках команды могут быть записаны правильно, их выполнение не будет приводить к нужному результату.
А теперь сами попробуем составить несколько алгоритмов для чертёжника:
Изобразим ромб с вершинами в точках (1,3), (2,5), (3,3), (2, 1).
Так как, в начале работы, чертёжник находится в точке (0, 0) и его перо поднято, для выполнения данной задачи необходимо сначала, установить чертёжника в одну из вершин ромба, и опустить перо. Зададим Чертёжнику соответствующие команды.
сместиться в точку (1,3)
Далее мы будем рисовать стороны ромба, обходя его вершины. Для этого нам достаточно задать Чертёжнику команды:
сместиться в точку (2,5)
сместиться в точку (3,3)
сместиться в точку (2,1)
сместиться в точку (1,3)
Запустим программу на выполнение
Так мы составили программу, для рисования фигуры по фиксированным точкам, теперь рассмотрим другую задачу.
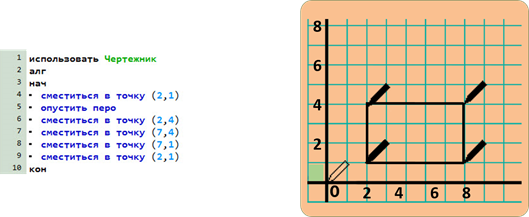
Изобразим прямоугольник, длиной 5 и шириной 3, со сторонами параллельными осям координат.
На координатной плоскости данный прямоугольник должен выглядеть так.
Мы можем зафиксировать одну из вершин прямоугольника в точке (2, 1), рассчитать расположение остальных его вершин, после чего нарисовать стороны прямоугольника путём обхода его по вершинам. Можно записать этот алгоритм для чертёжника в виде программы:
сместиться в точку (2,1)
сместиться в точку (2,4)
сместиться в точку (7,4)
сместиться в точку (7,1)
сместиться в точку (2,1)
Результатом ее выполнения будет рисунок…
Но данный алгоритм будет работать лишь до тех пор, пока первая вершина прямоугольника находится в точке (2, 1). Если зафиксировать первую вершину в другом месте, то и остальные вершины должны изменить своё положение.
Поэтому данную задачу мы будем решать иначе.
Обозначим данный прямоугольник ABCD, где А – его первая вершина. Пусть она имеет координаты (x,y), так как ширина прямоугольника 3, вершина B должна находиться на 3 единицы выше вершины А, следовательно, она будет иметь координаты (x, y+3). Так как длина прямоугольника 5, вершина C – должна находиться на 5 единиц правее вершины B, тогда её координаты (x+5, y+3). Так как вершина D должна быть на 3 единицы ниже вершины С, ее координаты (x+5, y).
Для примера мы установим первую вершину прямоугольника в точке (1, 1)
Теперь для изменения положения прямоугольника достаточно изменить первую команду.
Из решённых задач можно сделать вывод:
Команда абсолютного смещения служит для привязки рисунка, к определённым точкам координатной плоскости. Обычно ее используют для установки начального положения чертёжника.
Команда относительного смещения используется, когда положение рисунка не важно.
На этом уроке мы познакомились с исполнителем Чертёжник. Напомним наиболее важные моменты урока:
С помощью Чертёжника можно строить рисунки на координатной плоскости.
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
Управление исполнителем Чертёжник
§ 18. Управление исполнителем Чертёжник
ИНФОРМАТИКА. 6 КЛАССА. БОСОВА Л.Л. ОГЛАВЛЕНИЕ
Знакомимся с Чертёжником
Ключевые слова:
• исполнитель Чертёжник
• абсолютное смещение
• относительное смещение
• вспомогательный алгоритм
• основной алгоритм
• цикл п раз
Исполнитель Чертёжник предназначен для построения рисунков на координатной плоскости.
При задании точек этой координатной плоскости, в отличие от того, как это принято в математике, координаты х и у разделяются запятой. Например, координаты выделенной на рис. 63 точки будут записаны так: (1, 1).
Чертёжник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остаётся след — отрезок от предыдущего положения пера до нового. При перемещении поднятого пера никакого следа на плоскости не остаётся. В начальном положении перо Чертёжника всегда поднято и находится в точке (0, 0).
По команде поднять перо Чертёжник поднимает перо. Если перо уже было поднято, Чертёжник игнорирует эту команду: он не меняет положение пера и не сообщает об отказе. Иначе говоря, каким бы ни было положение пера до команды поднять перо, после этой команды оно будет поднятым.
Точно так же, независимо от первоначального положения, после выполнения команды опустить перо оно оказывается опущенным, т. е. готовым к рисованию.
Рисунки Чертёжник выполняет с помощью команд сместиться в точку и сдвинуться на вектор.
По команде сместиться в точку (а, Ь) Чертёжник сдвигается в точку с координатами (а, Ь). На рисунке 64 показаны результаты выполнения команды сместиться в точку (2, 3) при различных положениях пера до этой команды. Видно, что, независимо от предыдущего положения, перо оказывается в точке (2, 3), но длина и направление отрезка, который при этом чертится, могут быть различны. Команду сместиться в точку называют командой абсолютного смещения.
Назовите координаты точек, в которых находился Чертёжник до выполнения команды сместиться в точку (2, 3) (см. рис. 64).
В каком случае в результате выполнения команды сместиться в точку (2, 3) из некотрого показанного на рис. 64 начального положения не будет прочерчен ни один отрезок?
Пусть перо Чертёжника находится в точке (х, у). По команде (а, Ь) Чертёжник отсчитывает а единиц вправо вдоль горизонтальной оси (оси абсцисс), Ъ единиц вверх вдоль вертикальной оси (оси ординат) и сдвигает перо в точку с координатами (х + а; у + Ъ). Таким образом, координаты, указанные в команде, отсчитываются не от начала координат, а относительно текущего положения пера Чертежника. Поэтому команду сместиться на вектор называют командой относительного смещения.
На рисунке 65 показаны результаты выполнения команды сместиться на вектор (2, 3) при различных положениях пера до этой команды. Из рисунка видно, что положение пера после этой команды зависит от его предыдущего положения, зато в результате получаются отрезки, длина и направление которых одинаковы.
В математике направленные отрезки называются векторами, отсюда и происходит название команды.
Назовите координаты точек, в которых находилось перо Чертёжника до выполнения команды сместиться на вектор (2, 3) и куда оно переместилось после выполнения этой команды.
Чертёжник может исполнять только правильно записанные команды. Например, если вместо команды сместиться на вектор написать сдвинь на вектор, то Чертёжник эту запись не поймёт и сразу же сообщит об ошибке. Ошибки в записи команд называются синтаксическими.
Алгоритм может содержать логические ошибки. Например, все команды могут быть записаны правильно, но в результате логической ошибки последовательность их выполнения не будет приводить к поставленной цели или выполнение некоторых команд приведёт к отказу.
Пример алгоритма управления Чертёжником
Изобразим с помощью Чертёжника треугольник, положение вершин которого на координатной плоскости определяется парами чисел (1, 1), (3, 5), (5, 2) (рис. 66).
Так как в начале работы перо Чертёжника всегда поднято, то для рисования треугольника с заданными координатами достаточно выполнить следующую последовательность команд:
сместиться в точку (1, 1) опустить перо
сместиться в точку (3, 5)
сместиться в точку (5, 2)
сместиться в точку (1, 1)?
Предложите другие варианты выполнения этого задания. При этом число команд не должно превышать пяти (есть пять других вариантов).
А теперь составим такой алгоритм управления Чертёжником, чтобы с его помощью в произвольном месте координатной плоскости можно было нарисовать прямоугольник со сторонами, параллельными координатным осям, длины которых равны 2 и 4 единицам.
Зафиксируем одну из вершин прямоугольника в точке (1, 1). Нужный рисунок на координатной плоскости может выглядеть, как показано на рис. 67.
Предложите другой вариант рисунка, удовлетворяющий заданным условиям: одна из вершин прямоугольника расположена в точке (1, 1), а длины его сторон равны 2 и 4 единицам. (Существуют ещё семь вариантов.)
Можно определить координаты каждой из вершин этого прямоугольника и для его изображения составить следующую программу:
сместиться в точку (1, 1)
сместиться в точку (1, 3)
сместиться в точку (5, 3)
сместиться в точку (5, 1)
сместиться в точку (1, 1)
Этот алгоритм не будет решать поставленную задачу, если изменить координаты начальной точки (рис. 68). Изменение координат одной из вершин повлечёт за собой пересчет координат всех вершин прямоугольника. Причём это придется делать самому разработчику алгоритма.
Воспользуемся для рисования прямоугольника командой относительного смещения.
Пусть (х, у) — координаты вершины А прямоугольника ABCD (рис. 69).
Тогда координаты вершины В можно записать как (х, у + 2), вершины С — как (х + 4, у + 2), вершины D — как (х + 4, у) (см. рис. 69).
Чтобы изобразить отрезок АВ, воспользуемся командой сместиться на вектор (0, 2).
В результате Чертёжник сдвинет перо из точки с координатами (х, у) в точку с координатами (х + 0, у + 2).
Если в качестве вершины А зафиксировать точку с координатами (1, 1), то программа будет выглядеть так:
сместиться в точку (l, 1)
сместиться на вектор(0, 2)
сместиться на вектор(4, 0)
сместиться на вектор(-4, 0)?
Для того чтобы нарисовать прямоугольник в другом месте координатной плоскости, например в точке с координатами (5, 5), достаточно изменить в этой программе только первую строку:
сместиться в точку (5, 5)
С помощью команды абсолютного смещения рисунок «привязывается» к строго определенным точкам координатной плоскости. Она используется чаще всего для установки начального положения пера Чертёжника.
Команды относительного смещения применяются для создания рисунков, у которых точное место не важно или которые нужно воспроизводить в разных местах.
Чертёжник учится, или Использование вспомогательных алгоритмов
Чертёжник может рисовать любые фигуры из отрезков, например цифры почтового индекса. Как известно, каждая такая цифра вписана в прямоугольник (рис. 70).
Условимся при рисовании каждой цифры за начальную точку брать левую нижнюю вершину соответствующего прямоугольника.
Для чего нужна последняя команда?
Для чего нужна первая команда? Для чего нужна последняя команда?
А теперь представьте, что для Чертёжника необходимо разработать алгоритм рисования почтового индекса города Красноярска — 660000.
Самый простой вариант — составить очень длинный алгоритм, в котором дважды повторить рисование цифры 6 и четырежды — цифры 0.
Но есть и другой способ. Оказывается, Чертёжник может «запомнить», как рисуется та или иная цифра. Для этого алгоритм рисования цифр 0 и 6 нужно оформить в виде вспомогательного алгоритма.
Вспомогательный алгоритм
Строка алг цифра_О называется заголовком алгоритма. Имя алгоритма — цифра О. Алгоритм рисования буквы помещается чуть правее между служебными словами нач и кон.
Вспомогательный алгоритм рисования цифры 6 оформите самостоятельно.
Приказ на выполнение вспомогательного алгоритма записывается в основном алгоритме.
В среде КуМир основной алгоритм для изображения индекса 660000 будет выглядеть так:
использовать Чертежник
алг индекс Красноярска
нач
цифра_6
цифра_6
цифра_0
цифра_0
цифра_0
цифра_0
кон
К какому типу алгоритмов относится этот основной алгоритм?
Цикл ПОВТОРИТЬ n РАЗ
При составлении алгоритмов довольно часто встречаются случаи, когда некоторую последовательность команд нужно выполнять несколько раз подряд. Для упрощения записи алгоритма в таких случаях можно использовать специальную конструкцию повторения.
Тогда основной алгоритм будет выглядеть так:
использовать Чертежник
алг ряд ромбов_1
нач
сместиться в точку (1,2)
нц 5 раз
опустить перо
ромб
поднять перо
сместиться на вектор (3, 0)
кц
кон
В общем виде конструкция повторения записывается так:
нц раз
Служебные слова нц и кц пишутся одно под другим. Чуть правее между ними записывается повторяющаяся последовательность команд (тело цикла). Число повторений — произвольное целое число. Именно столько раз при выполнении алгоритма будут повторены команды, образующие тело цикла.
Предложите вариант решения задачи о почтовом индексе Красноярска с использованием конструкции повторения.
Можно ли обойтись без вспомогательного алгоритма в следующих ситуациях (рис. 72)?
Вопросы и задания
1. Охарактеризуйте исполнителя Чертёжник.
2. Составьте для Чертёжника алгоритм рисования прямоугольника со сторонами, параллельными осям координат, если известны координаты его двух вершин: (2, 1) и (7, 5).
3. Составьте алгоритм управления Чертёжником, в результате выполнения которого в произвольном месте координатной плоскости будет нарисован квадрат, длина стороны которого равна 2 единицам.
4. Составьте алгоритм управления Чертёжником, в результате выполнения которого в произвольном месте координатной плоскости будет нарисован прямоугольник, длины сторон которого равны 3 и 4 единицам.
5. Составьте алгоритм рисования изображенных ниже фигур так, чтобы в процессе рисования перо не отрывалось от бумаги и ни одна линия не проводилась дважды.
6. Оформите вспомогательные алгоритмы для рисования букв «М», «И», «Р». Составьте алгоритмы рисования слов «МИР», «РИМ», «МИМ».
7. Разработайте вспомогательный алгоритм рисования домика. На его основе составьте основной алгоритм рисования улицы из пяти домиков.
8. Составьте алгоритмы управления Чертёжником, после исполнения которых будут получены следующие рисунки:
9. Составьте алгоритмы управления Чертёжником, после исполнения которых будут получены следующие рисунки:
10. Придумайте свои задачи для Чертёжника.
§ 18. Управление исполнителем Чертёжник
Что значит сместиться на вектор в чертежнике
Исполнитель Чертёжник предназначен для построения рисунков на координатной плоскости.
При задании точек этой координатной плоскости, в отличие от того, как это принято в математике, координаты х и у разделяются запятой.
Чертёжник имеет перо, которое можно поднимать, опускать и перемещать. При перемещении опущенного пера за ним остаётся след — отрезок от предыдущего положения пера до нового. При перемещении поднятого пера никакого следа на плоскости не остаётся. В начальном положении перо Чертёжника всегда поднято и находится в точке (0, 0).
По команде поднять перо Чертёжник поднимает перо. Если перо уже было поднято, Чертёжник игнорирует эту команду: он не меняет положение пера и не сообщает об отказе. Иначе говоря, каким бы ни было положение пера до команды поднять перо, после этой команды оно будет поднятым.
Точно так же, независимо от первоначального положения, после выполнения команды опустить перо оно оказывается опущенным, т. е. готовым к рисованию.
Рисунки Чертёжник выполняет с помощью команд сместиться в точку и сдвинуться на вектор.
По команде сместиться в точку (а, b ) Чертёжник сдвигается в точку с координатами (а, b ).
На рисунке показаны результаты выполнения команды сместиться в точку (2, 3) при различных положениях пера до этой команды. Видно, что, независимо от предыдущего положения, перо оказывается в точке (2, 3), но длина и направление отрезка, который при этом чертится, могут быть различны. Команду сместиться в точку называют командой абсолютного смещения.
Команду СМЕСТИТЬСЯ НА ВЕКТОР (а, b ) называют командой относительного смещения.
По команде сместиться на вектор (а, b ) Чертёжник отсчитывает а единиц вправо вдоль горизонтальной оси (оси абсцисс), b единиц вверх вдоль вертикальной оси (оси ординат) и сдвигает перо в точку с координатами (х + а; у + b ). Таким образом, координаты, указанные в команде, отсчитываются не от начала координат, а относительно текущего положения пера Чертежника.
На рисунке показаны результаты выполнения команды сместиться на вектор (2, 3) при различных положениях пера до этой команды. Из рисунка видно, что положение пера после этой команды зависит от его предыдущего положения, зато в результате получаются отрезки, длина и направление которых одинаковы.
В математике направленные отрезки называются векторами, отсюда и происходит название команды.
Чертёжник может исполнять только правильно записанные команды. Например, если вместо команды сместиться на вектор написать сдвинь на вектор, то Чертёжник эту запись не поймёт
и сразу же сообщит об ошибке. Ошибки в записи команд называются синтаксическими.
Алгоритм может содержать логические ошибки. Например, все команды могут быть записаны правильно, но в результате логической ошибки последовательность их выполнения не будет приводить к поставленной цели или выполнение некоторых команд приведёт к отказу.
А теперь составим такой алгоритм управления Чертёжником, чтобы с его помощью в произвольном месте координатной плоскости можно было нарисовать прямоугольник со сторонами, параллельными координатным осям, длины которых равны 2 и 4 единицам.
Зафиксируем одну из вершин прямоугольника в точке (1, 1). Нужный рисунок на координатной плоскости может выглядеть, как показано
Предложите другой вариант рисунка, удовлетворяющий заданным условиям: одна из вершин прямоугольника расположена в точке (1, 1), а длины его сторон равны 2 и 4 единицам. (Существуют ещё семь вариантов.) Можно определить координаты каждой из вершин этого прямоугольника и для его изображения составить следующую программу:
Предложите другой вариант рисунка, удовлетворяющий заданным условиям: одна из вершин прямоугольника расположена в точке (1, 1), а длины его сторон равны 2 и 4 единицам. (Существуют ещё семь вариантов.) Можно определить координаты каждой из вершин этого прямоугольника и для его изображения составить следующую программу:
Изменение координат одной из вершин повлечёт за собой пересчет координат всех вершин прямоугольника. Причём это придется делать самому разработчику алгоритма. Воспользуемся для рисования прямоугольника командой относительного смещения.
Пусть (х, у) — координаты вершины А прямоугольника ABCD. Тогда координаты вершины В можно записать как (х, у + 2), вершины С — как (х + 4, у + 2), вершины D — как (х + 4, у) смотрите рисунок ниже
Чтобы изобразить отрезок АВ, воспользуемся командой сместиться на вектор (О, 2).
Начертить цифру ноль.
Цикл ПОВТОРИТЬ n РАЗ
Необходимо нарисовать вот такой рисунок из пяти одинаковых ромбов
Рисование ромба можно оформить в виде вспомогательного алгоритма:
Тогда основной алгоритм будет выглядеть так:
СМЕСТИТЬСЯ В ТОЧКУ (1, 2)
СМЕСТИТЬСЯ НА ВЕКТОР (1, 2)
СМЕСТИТЬСЯ НА ВЕКТОР (-1, 2)
СМЕСТИТЬСЯ НА ВЕКТОР (3, 0)
Служебные слова нц и кц пишутся одно под другим. Чуть правее между ними записывается повторяющаяся последовательность команд (тело цикла). Число повторений — произвольное целое число. Именно столько раз при выполнении алгоритма будут повторены команды, образующие тело цикла.