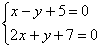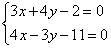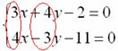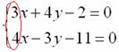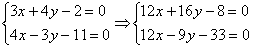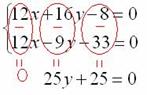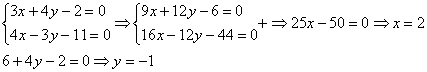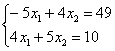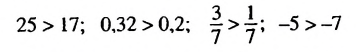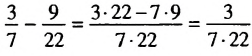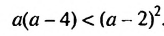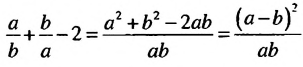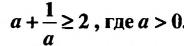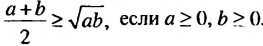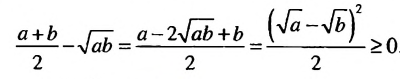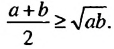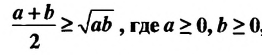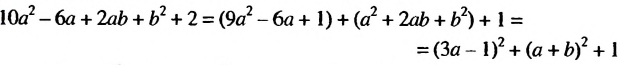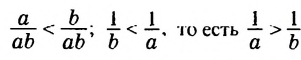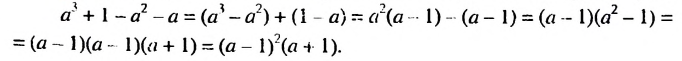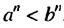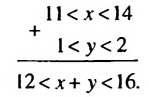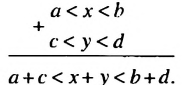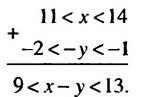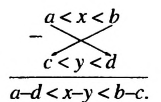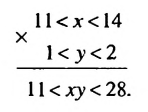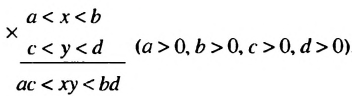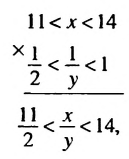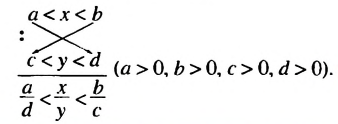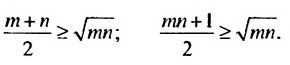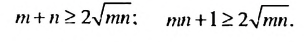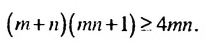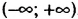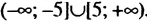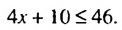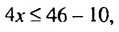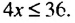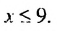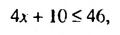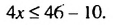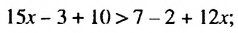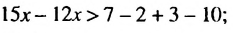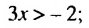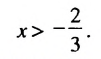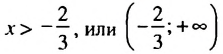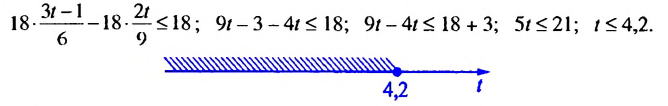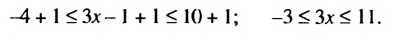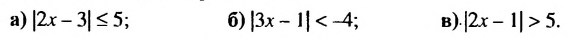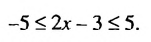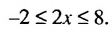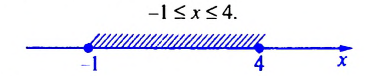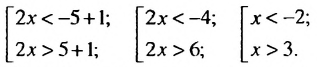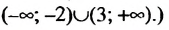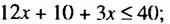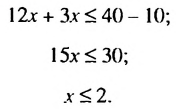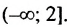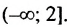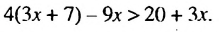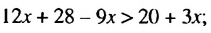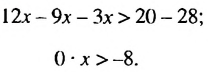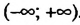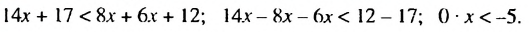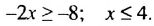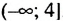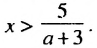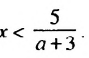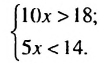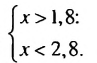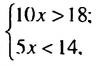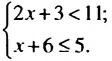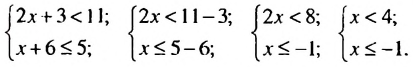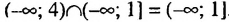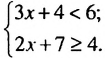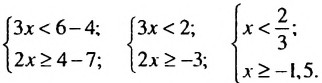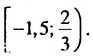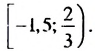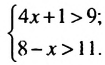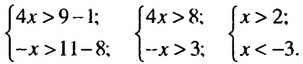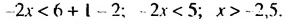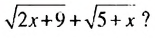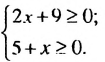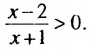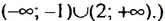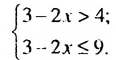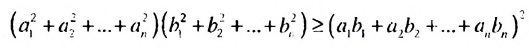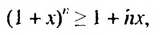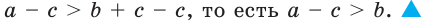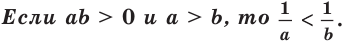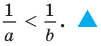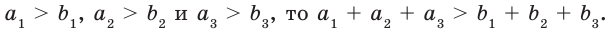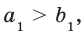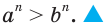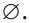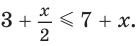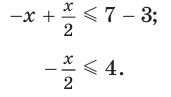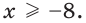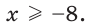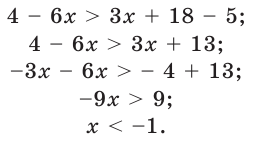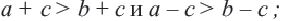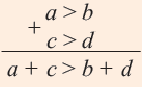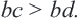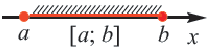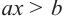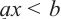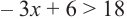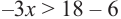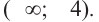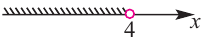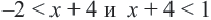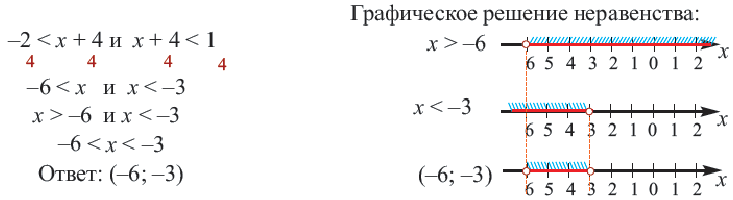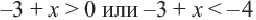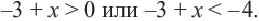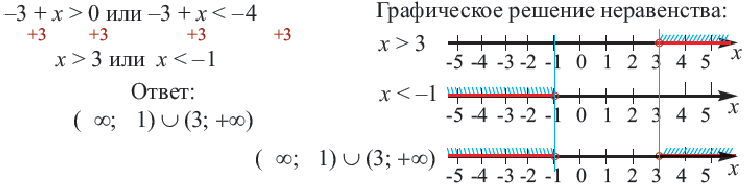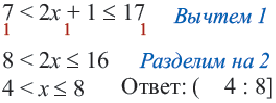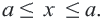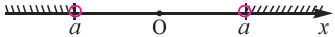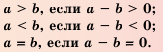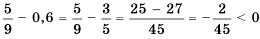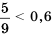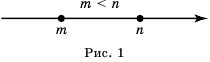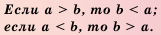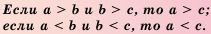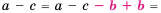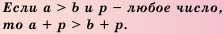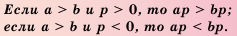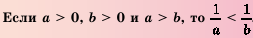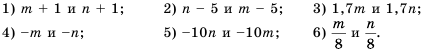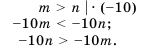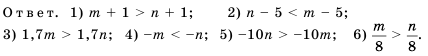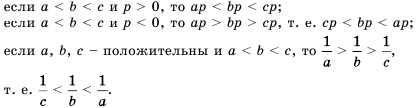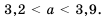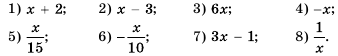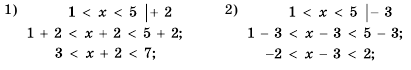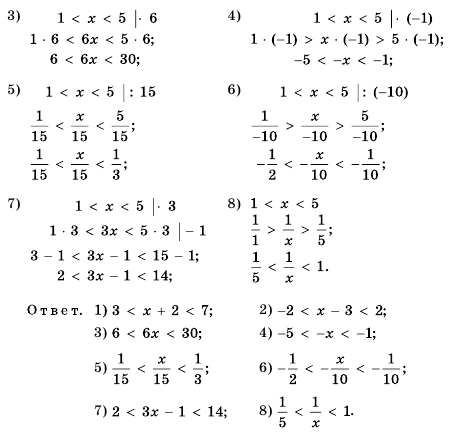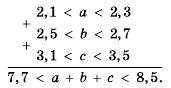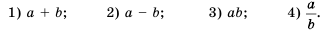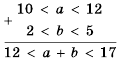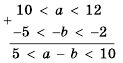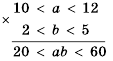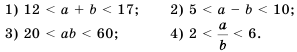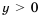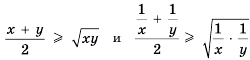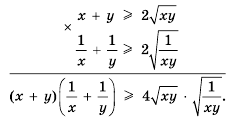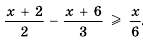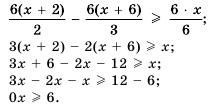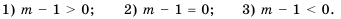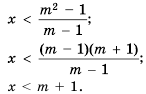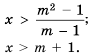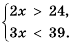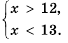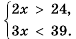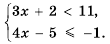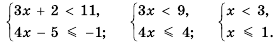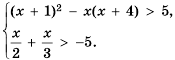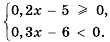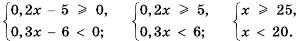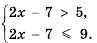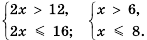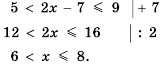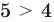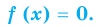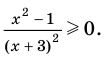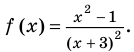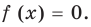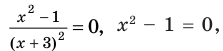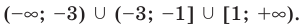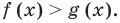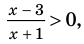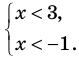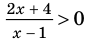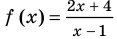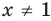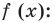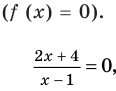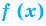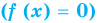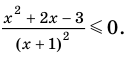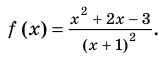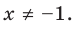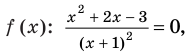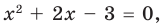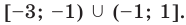Что значит сложить почленно
Решение системы методом почленного сложения (вычитания) уравнений системы
В ходе решения систем линейных уравнений нужно стараться использовать не «школьный метод», а метод почленного сложения (вычитания) уравнений системы. Почему? Это экономит время и упрощает вычисления, как сейчас увидите.
Пример 4:
Решить систему линейных уравнений:
Мы взяли ту же систему, что и в первом примере.
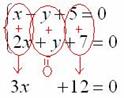
Анализируя систему уравнений, замечаем, что коэффициенты при переменной y одинаковы по модулю и противоположны по знаку (–1 и 1). В такой ситуации уравнения можно сложить почленно:
Действия, обведенные красным цветом, выполняются МЫСЛЕННО. Как видите, в результате почленного сложения у нас пропала переменная y.
В этом и состоит суть метода – избавиться от одной из переменных.
Теперь всё просто: 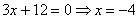
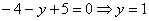
В чистовом оформлении решение должно выглядеть примерно так:
Пример 5:
Решить систему линейных уравнений:
В данном примере можно использовать «школьный» метод, но большой минус состоит в том, что когда мы будем выражать какую-либо переменную из любого уравнения, то получим решение в обыкновенных дробях. А возня с дробями займет время, к тому же, если у Вас не «набита рука» на действиях с дробями, то велика вероятность допустить ошибку.
Поэтому целесообразно использовать почленное сложение (вычитание) уравнений. Анализируем коэффициенты при соответствующих переменных:
Как видим, числа в парах (3 и 4), (4 и –3) – разные, поэтому, если сложить (вычесть) уравнения прямо сейчас, то от переменной мы не избавимся. Хотелось бы видеть в одной из пар одинаковые по модулю числа, например, 20 и 20 либо 20 и –20.
Будем рассматривать коэффициенты при переменной x:
Подбираем такое число, которое делилось бы и на 3 и на 4, причем оно должно быть как можно меньше. В математике такое число называется наименьшим общим кратным. Если Вы затрудняетесь с подбором, просто перемножьте коэффициенты: 3∙4 = 12.
Далее первое уравнение умножаем на число
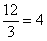
Второе уравнение умножаем на число 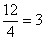
Вот теперь из первого уравнения почленно вычитаем второе.
На всякий случай приведём еще раз действия, которые проводятся мысленно:
Следует отметить, что можно было бы сделать и наоборот – из второго уравнения вычесть первое, это ничего не меняет. Начисто запишем:

Теперь подставим вычисленное значение переменной (y) в одно из уравнений системы. Например, в первое:
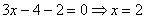
Ответ: 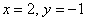
Решим систему другим способом. Рассмотрим коэффициенты при переменной (y):
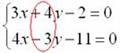
Очевидно, что вместо пары коэффициентов (4 и –3) нам нужно получить 12 и –12.
Для этого первое уравнение умножаем на 3, второе уравнение умножаем на 4:

Почленно складываем уравнения и находим значения переменных:
Ответ:
Пример 6:
Решить систему линейных уравнений:
Это пример для самостоятельного решения (ответ в конце урока).
Содержание:
Неравенства
Существует много задач, при решении которых нужно сравнить некоторые числа или величины, найти значения переменной, удовлетворяющие некоторому неравенству.
В этом параграфе мы выясним свойства числовых неравенств, как доказывать неравенства, что такое неравенство с переменной и система неравенств с переменной, как решать неравенства и их системы.
Числовые неравенства
Вы знаете, что записи
являются примерами числовых неравенств. Вы научились сравнивать натуральные числа, дроби, рациональные и действительные числа.
Известно, что 25 > 17. Найдем разность левой и правой частей этого неравенства:
Найдем разность левой и правой частей неравенства 7 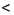
Из равенства 15=15 имеем:
15-15 = 0 — разность равна нулю.
Следовательно, существует зависимость между соотношениями «>», «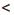
Определение:
Так как разность чисел а и b может быть либо положительной, либо отрицательной, либо равна нулю, то для любых чисел а и b выполняется одно и только одно из трех соотношений: а > b, a 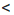
Используя данное определение, сравним числа 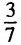
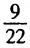
Разность данных чисел — число положительное, поэтому 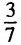
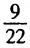
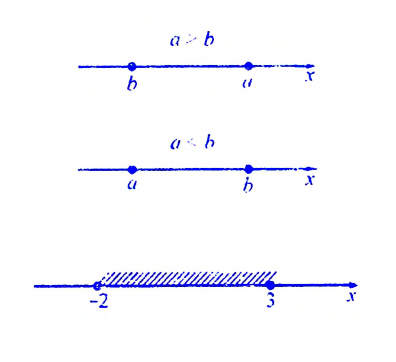
На координатной прямой большее число изображают точкой, которая лежит правее точки, изображающей меньшее число (см. рис. 1).
Рис. 1
В неравенствах используют знаки: «>» — меньше, «>» — больше, «≤ »— меньше или равно (не больше), «≥» — больше или равно (не меньше).
Неравенства, образованные при помощи знаков «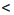
Числовые неравенства могут быть верными и неверными. Например, 5 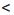
Доказательство неравенств
Докажем, что при любом значении а справедливо неравенство
Для этого образуем разность левой и правой частей неравенства и преобразуем ее:
Пример:
Доказать неравенство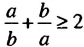
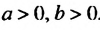
Решение:
Образуем разность левой и правой частей неравенства и преобразуем ее:
Разность мы представили в виде дроби, числитель которой неотрицателен, так как он является квадратом некоторого числа, а знаменатель положителен как произведение положительных чисел. Поэтому эта дробь, а значит и разность, неотрицательны: 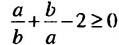
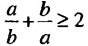
Если в доказанном неравенстве принять, что b = 1, то получим верное неравенство:
Итак, сумма двух положительных взаимно обратных чисел не меньше 2.
Пример:
Доказать неравенство
Решение:
Образуем разность левой и правой частей неравенства и преобразуем ее:
Следовательно,
Для положительных чисел а и b число 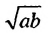
справедливо и при любых положительных числах а и b. 11оэтому среднее арифметическое двух положительных чисел не меньше их среднего геометрического.
Пример:
Решение:
Примечание. При доказательстве неравенства при помощи определения соотношений «больше», «меньше» или «равно» разность левой и правой части неравенства нужно преобразовать так, чтобы можно было определить знак разности.
Выражение, полученное после преобразований, принимает неотрицательные значения, если оно является, например, суммой, произведением или частным неотрицательных чисел, четной степенью некоторого выражения и т. п.
Выражение принимает отрицательные значения, если оно является суммой отрицательных чисел, произведением или частным чисел разных знаков и т. п.
Свойства числовых неравенств
Свойство 1 | Если а > b, то b 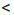
Свойство 2 | Если а 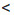
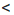
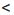
Геометрическая иллюстрация свойства 2 представлена на рисунке 3.

Аналогично можно доказать утверждение: если а > b и b > с, то а > с.
Свойство 3 | Если к обеим частям верною неравенства прибавить одно и то же число, то получим верное неравенство.
Аналогично проводится доказательство для случая а > b и любого числа с.
Следствие. Если некоторое слагаемое перенести из одной части верного неравенства в другую, изменив при этом знак слагаемого на противоположный. то получим верное неравенство.
Свойство 4 | Если обе части верною неравенства умножить или разделить на одно и то же положительное число, то получим верное неравенство. Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получим верное неравенство.
Доказательство: Пусть а 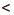
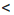
Аналогично проводится доказательство, если имеем неравенство а > b.
Справедливой является и часть свойства, касающаяся деления обеих частей неравенства на некоторое число, так как деление можно заменить умножением на число, обратное делителю.
Следствие. Если a и b — положительные числа и а 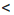
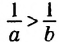
Доказательство: Разделим обе части неравенства а 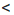
Это следствие можно использовать при сравнении чисел, обратных данным. Например, поскольку 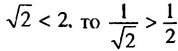
Замечание. Двойное неравенство а 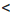
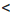
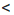
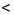
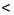
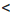
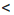
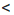
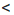
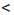
Итак, если ко всем частям верного двойною неравенства прибавить одно и то же число, то получим верное двойное неравенство.
Аналогично можно обосновать утверждения:
Пример:
Известно, что —1 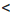
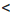
Решение:
Пример:
Решение:
Образуем разность левой и правой частей неравенства и преобразуем её:
Сложение и умножение числовых неравенств. Оценка значений выражений
Рассмотрим действия, которые можно выполнять над верными числовыми неравенствами.
Сложение числовых неравенств
Свойство 5 | Если почленно сложить верные неравенства одного знака, сохранив их общий знак, то получим верное неравенство.
Доказательство: Пусть а 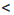
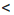
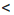
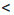
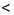
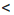
Аналогично можно доказать, что если а > b и с > d, то а + с > b + d.
Умножение числовых неравенств
Возьмем верные неравенства: 7 > 2 и 5 > 3. Почленно перемножим их. Получим верное неравенство 7 • 5 > 2 • 3 или 35 > 6.
В первом случае все числа данных неравенств были положительными, во втором — положительными и отрицательными. Докажем следующее свойство.
Свойство 4 | Если почленно перемножить верные неравенства одного знака, левые и правые части которых — положительные числа, сохранив при этом их общий знак, то получим верное неравенство.
Доказательство: Пусть а 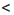
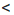
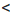
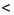
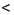
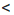
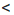
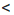
Аналогично можно доказать, что если а > b и с > d, где а, b, с и d — положительные числа, то ас > bd.
Следствие. Если а 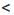
При доказательстве следствия достаточно взять н неравенств а 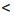
Оценка значений выражений
Пример:
Решение:
а) Оценим сумму х + у.
Применим к неравенствам 11 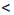
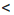
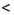
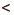
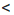
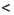
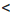
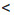
Сокращенно эти преобразования записывают так:
Общая схема оценки суммы имеет такой вид:
Общая схема оценки разности имеет такой вид:
в) Оценим произведение ху.
Поскольку 11 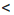
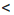
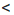
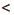
Сокращенно эти преобразования записывают гак:
Общая схема оценки произведения имеет такой вид:
г) Оценим частное 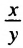
Представим частное 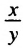
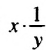
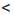
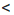
то 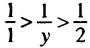
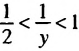
то есть 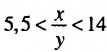
Общая схема оценки частного имеет такой вид:
Пример:
Доказать неравенство (m + n)(mn + l) ≥ 4mn, где m ≥ 0, n ≥ 0.
Решение:
Используем известное неравенство 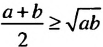
Запишем это неравенство для чисел m и n, а потом — для чисел mn и 1. Получим два верных неравенства:
Умножим обе части каждого неравенства на 2:
Почленно перемножив эти неравенства, получим:
Примечание. При доказательстве неравенства из примера 1 мы использовали известное неравенство, доказанное ранее. Особенность использованного способа доказательства неравенств состоит в том, что:
Неравенства с одной переменной. Числовые промежутки
Понятие о неравенстве с одной переменной и его решении
Рассмотрим неравенство 2х + 5 > 11. При одних значениях x данное неравенство превращается в верное числовое неравенство, при других — в неверное. Например, при х = 5 получим верное числовое неравенство 2 • 5 + 5 > 11; 15 > 11, а при х = 1 получим неверное числовое неравенство 2 • 1 + 5 > 11; 7 > 11.
Если нужно найти все значения х, при которых неравенство 2х + 5 > 11 является верным, то говорят, что нужно решить неравенство 2х + 5 > 11, содержащее одну переменную х.
При х = 5 неравенство 2х + 5 > 11 является верным. Говорят, что число 5 является решением данного неравенства или удовлетворяет данному неравенству.
Определение: Решением неравенства с одной переменной называют значение переменной, превращающее его в верное числовое неравенство.
Решить неравенство значит найти все его решения или доказать, что решений нет.
Неравенство с одной переменной преимущественно имеет бесконечное множество решений. Так, решениями неравенства 2х + 5 > 11 являются числа
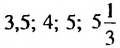
Числовые промежутки
Рассмотрим несколько примеров.

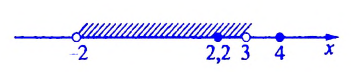


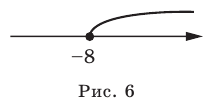
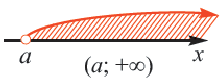
4) Неравенству х >4 удовлетворяют все действительные числа больше 4. На координатной прямой чти числа изображают точками, лежащими справа от точки с координатой 4. Множество чисел, удовлетворяющих неравенству х > 4, изображают полупрямой, находящейся справа от точки с координатой 4 без этой точки (см. рис. 8). Такое множество называют промежутком от 4 до плюс бесконечности и обозначают (4; 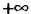

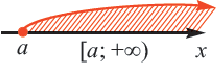
Множество чисел, удовлетворяющих неравенству х ≥ 4, изображают полупрямой (см. рис. 9). Это множество обозначают [4; 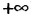

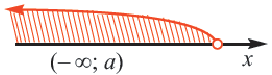
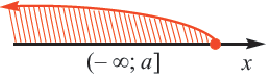
5) Множество чисел, удовлетворяющих неравенству х 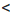
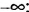
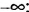


6) Множество всех действительных чисел изображают всей координатной прямой и обозначают так:
Объединение и пересечение числовых промежутков
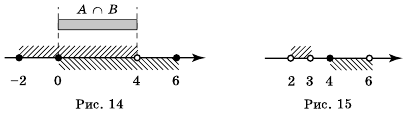
Рассмотрим два промежутка: [-1; 4) и (2; 7).

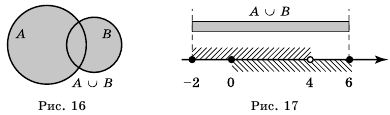
Промежуток [-1; 7) образуют все числа, принадлежащие промежутку [-1; 4) или промежутку (2: 7). Говорят, что промежуток [-1; 7) является объединением промежутков [-1;4) и (2; 7). Записывают: 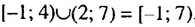
Определение: Объединением числовых промежутков называют множество всех чисел, принадлежащих хотя бы одному из этих промежутков.
Промежуток (2; 4) образуют все общие числа из промежутков [-1; 4) и (2; 7), то есть все числа, принадлежащие каждому из промежутков [-1; 4) и (2; 7). Говорят, что промежуток (2; 4) является пересечением промежутков [-1; 4) и (2; 7). Записывают: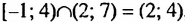
Определение: Пересечением числовых промежутков называют множество всех чисел, принадлежащих каждому из этих промежутков.
Для тех, кто хочет знать больше.
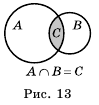
Объединением и пересечением двух числовых промежутков могут быть не числовые промежутки. Рассмотрим, например, промежутки [-2; 1] и (3;4). Чисел, принадлежащих обоим этим промежуткам, пет (см. рис. 12). Поэтому говорят, что пересечением этих промежутков является пустое множество. Его обозначают символом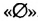
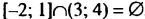
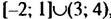
Для промежутков 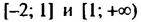
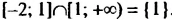
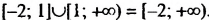

Пример:
Указать наименьшее и наибольшее действительные числа, принадлежащие промежутку:
Решение: а) 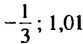
в) наименьшего числа нет; 4,8;
г) ни наименьшего, ни наибольшего чисел нет.
Пример:
Отметить на координатной прямой множество чисел, удовлетворяющих неравенству, и записать это множество в виде промежутка или объединения промежутков: а) 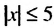
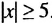
Решение:
а) Модулем числа х является расстояние от начала отсчета до точки, изображающей число х на координатной прямой. Поэтому решениями данного неравенства являются числа, соответствующие тем точкам координатной прямой, которые лежат от начала отсчета на расстоянии не больше 5.
Следовательно, решениями неравенства 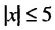
б) Решениями неравенства 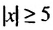
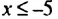
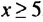
Следовательно, множеством решений неравенства 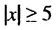
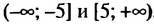
Решение неравенств с одной переменной. Равносильные неравенства
Пример:
Одна сторона участка прямоугольной формы на 5 м длиннее другой. Какими могут быть стороны участка, чтобы для его ограждения хватило сетки длиной 46 м?
Решение:
Пусть длина меньшей стороны участка равна х м, тогда длина большей —
(х + 5 )м, а периметр участка — 2(х + х + 5) = (4х + 10) (м). По условию периметр не превышает 46 м. поэтому 4х + 10 ≤ 46.
Чтобы найти стороны участка, нужно решить неравенство 4х + 10 ≤ 46 с одной переменной х.
При решении неравенства его преобразуют, заменяя более простыми неравенствами с теми же решениями.
Неравенства, имеющие одни и тс же решения, называют равносильными. Неравенства, не имеющие решений, также называют равносильными.
Замену неравенства равносильным» ему неравенствами выполняют на основании таких свойств:
Используя эти и свойства, решим неравенство:
Перенесем слагаемое 10 из левой части неравенства в правую с противоположным знаком, получим неравенство
равносильное заданному неравенству.
Разделив обе части последнего неравенства на 4, получим неравенство
Следовательно, неравенство 4х + 10 ≤ 46 равносильно неравенству х ≤ 9, и ему удовлетворяют все числа не больше 9 (см. рис. 16). Множество решений данного неравенства можно записать в виде числового промежутка 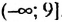

Вернемся к задаче. Длину меньшей стороны участка мы обозначили через х м. Поскольку длина стороны выражается положительным числом, то х может принимать значения из промежутка (0; 9|. Итак, меньшая сторона участка не должна превышать 9 м, большая же сторона на 5 м длиннее нее.
Для тех, кто хочет знать больше.
мы перенесли слагаемое 10 из левой части неравенства в правую с противоположным знаком и получили неравенство
Докажем, что неравенства (1) и (2) равносильны.
Пусть х = а — любое решение неравенства (1), тогда 4а + 10 ≤ 46 — верное числовое неравенство. Перенесем слагаемое 10 из левой части неравенства в правую, изменив его знак на противоположный, получим верное числовое неравенство 4а ≤ 46- 10. Из того, что последнее неравенство является верным, следует, что число а является решением неравенства (2).
Мы показали, что любое решение неравенства (1) является решением неравенства (2) и любое решение неравенства (2) является решением неравенства (1). Поэтому эти неравенства имеют одни и те же решения, то есть являются равносильными.
Пример:
Решение:
перенесем слагаемые, содержащие переменную, в левую часть неравенства, а остальные — в правую часть:
приведем подобные слагаемые:
разделим обе части неравенства на 3:
Ответ.
Пример:
Решить неравенство 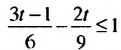
Решение:
Умножим обе части неравенства на наименьший общий знаменатель дробей, входящих в неравенство, то есть на 18. Получим:
Ответ, (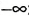
Пример:
Решить неравенство 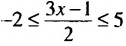
Решение:
Разделим все части неравенства на 3, получим: 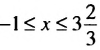
Ответ. 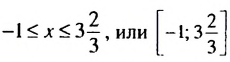
Пример:
Решить неравенство:
Решение:
а) Решениями неравенства |2х-3| ≤ 5 являются числа, удовлетворяющие двойному неравенству
Прибавим ко всем частям неравенства число 3, получим:
Разделим все части неравенства на 2:
Решая каждое неравенство совокупности, получим:
Решениями совокупности являются значения х, удовлетворяющие неравенству х 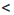
Ответ. х 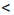
Линейные неравенства с одной переменной
Рассмотрим несколько примеров.
Пример:
Решить неравенство 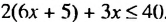
Решение:
Множеством решений неравенства является числовой промежуток
Ответ.
Пример:
Решить неравенство
Решение:
Ответ.
Пример:
Решить неравенство 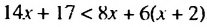
Решение:
Неравенство 0 • х 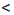
Неравенства вида ах > b, ax>b, ах 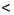
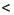
Если 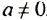
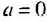
Пример:
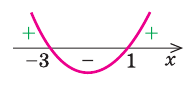
Найти область определения функции 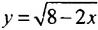
Решение:
Областью определения функции является промежуток 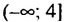
Ответ.
Пример:
Решить неравенство (а + 3)х 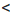
Решение:
Рассмотрим три случая: 1) а + 3 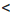
1) Если а + 3 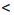
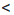
3) Если а + 3 > 0. то есть а > —3, то
Системы линейных неравенств с одной переменной
Понятие системы неравенств с одной переменной и ее решения
Пример:
Одна хозяйка купила на рынке 10 кг помидоров и заплатила за них больше 18 руб. Вторая хозяйка купила такие же помидоры и заплатила за 5 кг меньше 14 руб. По какой цене покупали помидоры хозяйки?
Решение:
Пусть цена 1 кг помидоров х руб., тогда 10 кг стоят 10х руб., что по условию задачи больше 18 руб., то есть 10х > 18.
5 кг помидоров стоят 5х руб., что по условию задачи меньше 14 руб., то есть 5х 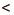
Чтобы решить задачу, нужно найти те значения х, при которых верным будет как неравенство 10х > 18, так и неравенство 5х 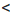
Если нужно найти те значения переменной, которые удовлетворяют двум неравенствам, то говорят, что нужно решить систему неравенств. Для нашей задачи систему записывают так:
Решив каждое из неравенств системы, получим:
Следовательно, значения х должны удовлетворять условию 1,8 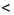
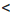
Значение х = 2 является решением обоих неравенств системы
поскольку каждое из числовых неравенств 10 • 2 > 18 и 5 • 2 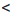
верным. Такое значение х называют решением системы неравенств.
Определение: Решением системы неравенств с одной переменной называют значение переменной, при котором выполняется каждое из неравенств системы.
Решить систему неравенств значит найти все ее решения или доказать, что их нет.
Решение систем линейных неравенств с одной переменной
Пример:
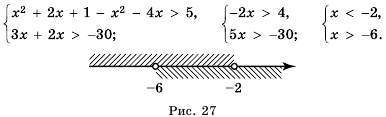
Решить систему неравенств
Решение:
Решим каждое из неравенств системы:
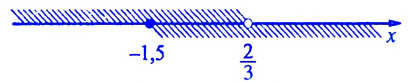
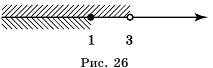
Отметим на координатной прямой множество чисел, удовлетворяющих первому неравенству последней системы, — промежуток 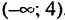
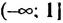
Общими решениями неравенств являются значения х, принадлежащие обеим промежуткам, то есть их пересечению:
Пример:
Решить систему неравенств
Решение:
На координатной прямой отметим множество чисел, удовлетворяющих неравенству 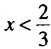
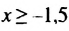
Общими решениями неравенств являются значения х, принадлежащие промежутку
Ответ.
Пример:
Решить систему неравенств
Решение:
На координатной прямой отметим множество чисел, удовлетворяющих неравенству х > 2, и множество чисел, удовлетворяющих неравенству х 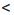
Общих решений неравенства не имеют.
Следовательно, систему линейных неравенств с одной переменной можно решить, используя следующую схему:
Примечание.
Пример:
Решить неравенство 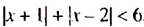
Решение:
Найдем значения х, при которых значения выражений, стоящих под знаком модуля, равны нулю:
Раскроем модули на каждом из промежутков и решим соответствующие неравенство.
Решим полученное неравенство:
Кроме того, значения х должны удовлетворять неравенству х 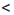
Значения х должны удовлетворять двум неравенствам: 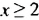
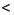
системе 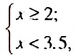
Пример:
При каких значениях х имеет смысл выражение
Решение:
Данное выражение имеет смысл при тех значениях х, при которых каждое из выражений 2х + 9 и 5 + х принимает неотрицательные значения. Поэтому искомые значения л должны удовлетворять систему неравенств
Решим полученную систему:
Пример:
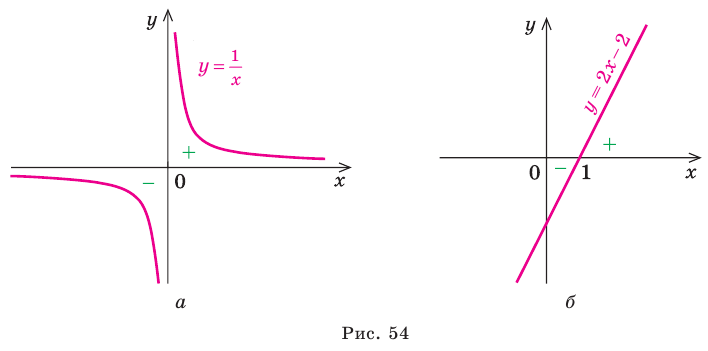
Решить неравенство
Решение:
Дробь положительна только тогда, когда ее числитель и знаменатель положительны или когда они оба отрицательны. Поэтому решение данного неравенства сводится к решению двух систем неравенств:
Решениями первой системы являются значения х, удовлетворяющие неравенству х > 2, а второй — неравенству х 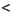
Ответ, х 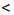
Пример:
Решить двойное неравенство 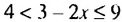
Решение:
Данное двойное неравенство можно записать в виде системы
Заметим, что двойное неравенство в упражнении 3 можно решать и на основании свойств равносильности неравенств (см. пункт 5, упражнение 3).
Как известно, возникновение чисел обусловлено потребностями практической деятельности человека. Применение чисел требовало умения их сравнивать. Делать это люди научились много тысячелетий назад.
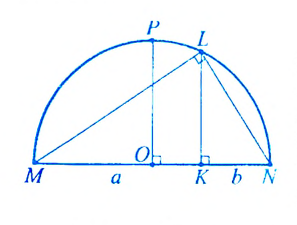
Где в «Началах» Евклида сугубо геометрически было обосновано неравенство 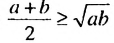
Рассмотрим геометрическую иллюстрацию неравенства
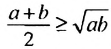
Отрезок РО — радиус полуокружности, поэтому 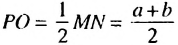
Поскольку 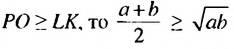
Это известное неравенство между средним арифметическим и средним геометрическим двух положительных чисел, которое можно распространить па случай большего количества чисел, называют еще неравенством Коши.
Огюстен Луи Коши — известный французский математик. Он является автором более 800 работ по арифметике и теории чисел, алгебре, математическому анализу, теоретической и небесной механике, математической физике и т. п. Были периоды, когда Коши каждую неделю подавал в Парижскую Академию наук новую математическую работу. Скорость, с какой Коши переходил от одного предмета к другому, позволила ему проложить в математике немало новых путей. Многие теоремы, определения, признаки носят его имя.
Приведем еще два известных неравенства, которые, как и неравенство Коши, используют для доказательства многих математических утверждений, в частности, для доказательства других неравенств.
Неравенство Коши — Буняковского:
где 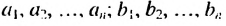
О В. Я. Буняковском читайте в рубрике «Отечественные математики».
где 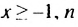
Якоб Бернулли — швейцарский математик, профессор Базельского университета. Основные его работы посвящены математическому анализу, но особое внимание ученый уделял теории вероятностей. Немало теорем названы его именем. Бернулли положил начало одному из разделов прикладной математики — математической статистике.
Неравенства
На практике вам часто приходится сравнивать величины. Например, площадь России (603,7 тыс. км2) больше площади Франции (551 тыс. км2), высота горы Роман-Кош (1545 м) меньше высоты горы Говерлы (2061 м), расстояние от Киева до Харькова (450 км) равно 0,011 длины экватора.
Когда мы сравниваем величины, нам приходится сравнивать числа. Результаты этих сравнений записывают в виде числовых равенств и неравенств, используя знаки =, >, b; если число а меньше числа b, то пишут а b и b > с, то а > с.
Аналогично доказывают свойство: если а b и с — любое число, то а + с > b + с.
Аналогично доказывают свойство: если а b + с верно. Вычтем из обеих его частей число с. Получим:
Поскольку деление можно заменить умножением 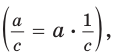
Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получим верное неравенство.
Если обе части верного неравенства умножить или разделить на одно и то же отрицательное число и изменить знак неравенства на противоположный, то получим верное неравенство.
Следствие:
Доказательство: 
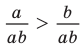
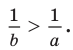
В теоремах этого пункта шла речь о строгих неравенствах. Нестрогие неравенства также обладают аналогичными свойствами. Например, если 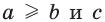
Сложение и умножение числовых неравенств. Оценивание значения выражения
Выводы из этих примеров интуитивно очевидны. Их справедливость подтверждают следующие теоремы.
Теорема: (о почленном сложении неравенств).
Аналогично доказывается свойство: если а b и с > d (или а b и с d) — неравенствами противоположных знаков.
Говорят, что неравенство а + с > b + d получено из неравенств а > b и с > d путем почленного сложения.
Теорема: означает, что при почленном сложении верных неравенств одного знака результатом является верное неравенство того же знака.
Отметим, что теорема 3.1 справедлива и в случае почленного сложения трех и более неравенств. Например, если
Теорема: (о почленном умножении неравенств). Если а > Ь, с > d и а, и, с, d — положительные числа, то ас > bd.
Аналогично доказывается свойство: если а bd получено из неравенств а > b и с > d путем почленного умножения.
Теорема: означает, что при почленном умножении верных неравенств одного знака, у которых левые и правые части — положительные числа, результатом является верное неравенство того же самого знака.
Заметим, что теорема 3.2 справедлива и в случае почленного умножения трех и более неравенств. Например, если 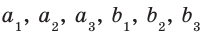
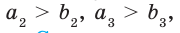
Следствие: Если 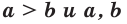
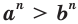
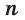
Доказательство: 
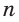
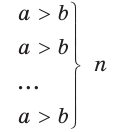
Так как а и b — положительные числа, то можем перемножить почленно 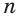
Заметим, что все рассмотренные свойства неравенств справедливы и в случае нестрогих неравенств:
Часто значения величин, являющихся результатами измерений, не точны. Измерительные приборы, как правило, позволяют лишь установить границы, между которыми находится точное значение.
Пусть, например, в результате измерения ширины х и длины у прямоугольника было установлено, что 2,5 см 44 является математической моделью задачи о периметре параллелограмма.
Если в это неравенство вместо переменной х подставить, например, число 16, то получим верное числовое неравенство 14 + 32 > 44. В таком случае говорят, что число 16 является решением неравенства 14 + 2х > 44.
Определение: Решением неравенства с одной переменной называют значение переменной, которое обращает его в верное числовое неравенство.
Так, каждое из чисел 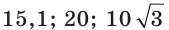
Замечание. Определение решения неравенства аналогично определению корня уравнения. Однако не принято говорить «корень неравенства».
Решить неравенство означает найти все его решения или доказать, что решений не существует.
Все решения неравенства образуют множество решений неравенства. Если неравенство решений не имеет, то говорят, что множеством его решений является пустое множество. Пустое множество обозначают символом
Например, в задаче «решите неравенство 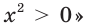
Очевидно, что неравенство 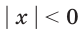
Определение: Неравенства называют равносильными, если они имеют одно и то же множество решений.
Приведем несколько примеров.
Неравенства 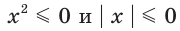
Неравенства 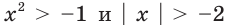
Так как каждое из неравенств 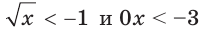
Решение линейных неравенств с одной переменной
Свойства числовых равенств помогали нам решать уравнения. Точно так же свойства числовых неравенств помогут решать неравенства.
Решая уравнение, мы заменяли его другим, более простым уравнением, но равносильным данному. По аналогичной схеме решают и неравенства.
При замене уравнения на равносильное ему уравнение используют теоремы о перенесении слагаемых из одной части уравнения в другую и об умножении обеих частей уравнения на одно и то же отличное от нуля число.
Аналогичные правила применяют и при решении неравенств.
С помощью этих правил решим неравенство, полученное в задаче о периметре параллелограмма (см. п. 4).
Разделим обе части неравенства на 2:
Заметим, что полученное неравенство равносильно исходному неравенству. Множество его решений состоит из всех чисел, которые больше 15. Это множество называют числовым промежутком и обозначают (15; +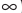
Точки координатной прямой, изображающие решения неравенства х > 15, расположены справа от точки, изображающей число 15, и образуют луч, у которого «выколото» начало (рис. 5).
Ответ может быть записан одним из способов: (15 ; + 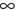
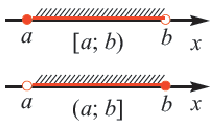
Заметим, что для изображения на рисунке числового промежутка используют два способа: с помощью либо штриховки (рис. 5, а), либо дуги (рис. 5, б). Мы будем использовать второй способ.
Пример:
Решите неравенство
Решение:
Перенесем слагаемое х из правой части неравенства в левую, а слагаемое 3 — из левой части в правую и приведем подобные члены:
Ответ можно записать одним из способов: 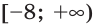
Пример:
Решите неравенство
Решение:
Запишем цепочку равносильных неравенств:
Неравенства
В этом разделе вы научитесь:
Это интересно!
Великий Азербайджанский мыслитель, философ, математик, астроном Насреддин Туси создал научные труды, которые внесли большой вклад в историю человечества. В письменных источниках его называют «Отецом тригонометрии». В своём труде «Об измерении круга» он впервые доказал теорему синусов и применил их для астрономических расчетов.
Неравенства:
Неравенства записываются при помощи знаков 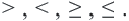
Для сравнения чисел и выражений применяются различные методы. Одним из них является метод оценки разности.
Пример:
Сравним выражения 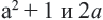
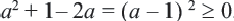
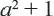
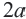
Свойства неравенств
Доказательство 3-го свойства: если 
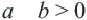

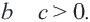
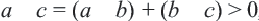
Исследование
Рассмотрим неравенство
При значении переменной меньше 7, значение суммы 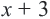
При значении переменной равной 7, значение суммы 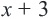
При значении переменной больше 7, значение суммы 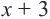
Неравенство 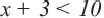
Свойства неравенств
Теорема. Если неравенство верное, то прибавив или отняв от обеих частей данного неравенства одно и то же число, получим верное неравенство.
Если 
Если 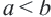
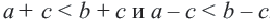
Пример:
Масса морского тюленя может достигать максимально 650 кг. В настоящее время тюлень весит 398 кг. Как при помощи неравенства можно записать массу, которую еще сможет набрать тюлень?
Свойства неравенств
Если обе части верного неравенства умножить или разделить на одно и то же положительное число, то получим верное неравенство.
Для любых чисел 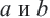

Если обе части верного неравенства разделить или умножить на одно и то же отрицательное число и поменять знак неравенства на противоположный, то получим верное неравенство.
Для любых чисел 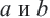

Сложение и вычитание неравенств
Теорема. Если
Если к обеим частям неравенства 
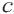
Если к обеим частям неравенства 
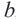
Из 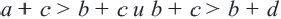
Данная теорема верна при сложении двух и более неравенств. Если почленно сложить верные неравенства одного знака, то получится верное неравенство.
Если 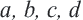



Если в неравенстве 
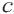

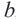

Отсюда следует что, 
Следствие. Если 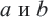


Числовые промежутки
При 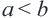
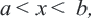
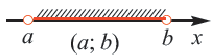
Если в множество точек интервала 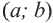
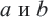
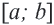
Множество всех чисел 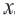
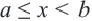
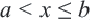
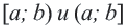
Множество всех точек, удовлетворяющих условию 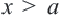
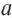
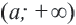
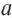
Если точка 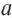
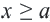
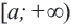
Множество всех чисел, удовлетворяющих условию 
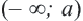
Если точка 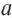
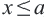
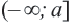
Решение линейных неравенств с одной переменной
Определение. Решением линейною неравенства с одной переменной называется множество всех значений переменной превращающих данное неравенство в верное.
Решить неравенство, значит найти все его решения или докатать, что решений нет. Неравенства, имеющие одинаковые множества решений, называются равносильными. Неравенства, не имеющие решения, также называются равносильными. При решении неравенств используются следующие следствия, полученные из свойств числовых неравенств:
1) Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.
2) Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство. Например, неравенство 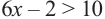


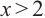
3) Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
Неравенства вида 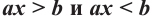
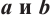
Решение неравенства
Решение неравенства
Пример:
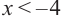
Графическое представление решения:
Решение двойных неравенств
Двойные неравенства
Пример 1. Запишем неравенство 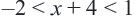
Надо найти такие значения 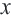
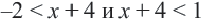
Пример 2.
Надо найти такие значения х, которые будут удовлетворять неравенствам
Решаем каждое неравенство и находим объединение множеств.
Пример 3. Двойное неравенство 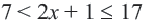
Простые неравенства с переменной, входящей под знаком модуля
Геометрически решением неравенства 
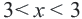
При 

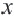
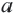
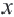
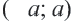
Поэтому неравенство 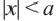
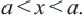
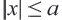
При 

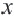
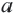
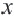
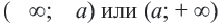
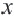
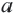

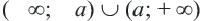
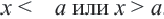
Множество решений неравенства 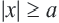
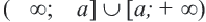
Неравенства
Числовые неравенства
Для любых двух чисел 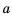
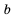
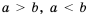
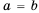
Известно, что 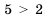
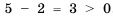
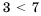
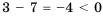
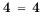
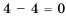
Приходим к определению сравнения чисел:
Пример №285
Сравнить 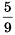
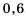
Решение:
Рассмотрим разность чисел 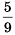
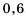
Разность отрицательна, значит 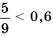
Ответ.
Напомним, что на координатной прямой точка, соответствующая меньшему числу, лежит левее точки, соответствующей большему числу. На рисунке 1 точка, соответствующая числу 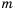
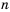
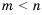
Числовые неравенства бывают верные и неверные.
Например, 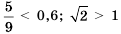
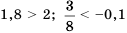
Кроме знаков 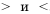
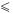
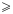
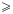
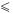
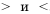
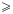
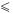
Из определения соотношений «больше», «меньше» и «равно» получаем, что 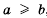
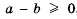
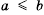
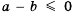
Рассмотрим, как с помощью определения сравнения чисел можно доказывать неравенства.
Пример №286
Доказать, что при любом значении 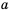
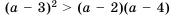
Доказательство: Рассмотрим разность левой и правой частей неравенства и упростим ее:
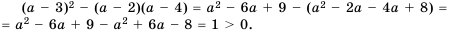
Так как 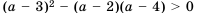
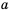
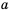
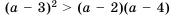
Условие для примера 2 можно было сформулировать проще, например: доказать неравенство 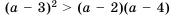
Пример №287
Доказать неравенство 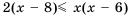
Доказательство: Рассмотрим разность левой и правой частей неравенства и упростим ее:
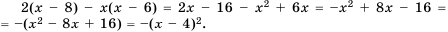
Так как 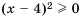
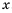
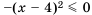
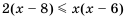
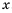
Пример №288
Доказать неравенство 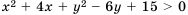
Доказательство: В левой части неравенства выделим квадраты двучленов:
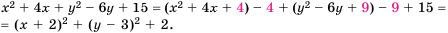
При любых значениях 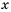
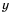
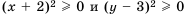
А значит, 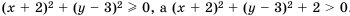
Следовательно, 
Напомним, что число 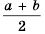
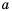
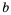
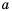
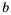
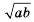
Пример №289
Доказать, что среднее арифметическое двух неотрицательных чисел 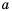
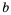
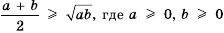
Доказательство: Рассмотрим разность левой и правой частей неравенства и преобразуем ее, учитывая, что 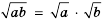
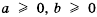
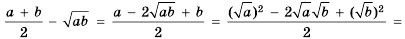
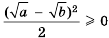
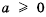
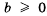
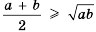
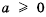
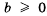
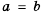
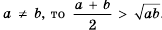

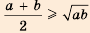
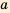
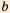
Чтобы оценить отношение длины круга 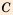
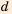
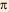
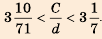
Привычные нам символы для записи неравенств появились лишь в XVII—XVIII в. Знаки 



Кроме неравенства Коши отметим еще и такие известные неравенства:
1) Неравенство Бернулли.

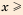
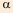
2) Неравенство Чебышёва.
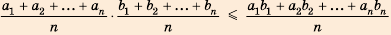
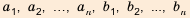
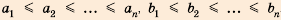
3) Неравенство Коши-Буняковского.
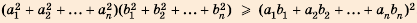
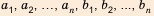
Основные свойства числовых неравенств
Рассмотрим свойства числовых неравенств.
Свойство 1.
Доказательство: Поскольку 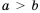
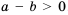
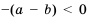
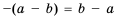
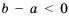
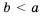
Аналогично будем рассуждать и в случае, когда 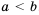
Свойство 2.
Доказательство: По условию 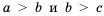
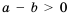
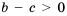
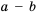

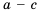
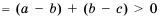
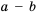

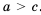
Аналогично рассуждаем, когда 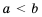
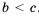
Геометрическая иллюстрация свойства 2 представлена на рисунках 2 и 3.
Свойство 3.
Доказательство: По условию 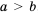
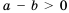
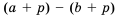
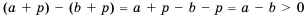
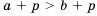
Следствие: 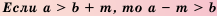
Доказательство: Так как 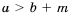
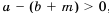


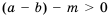
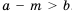
Из этого следствия имеем:
если некоторое слагаемое перенести из одной части верного неравенства в другую, изменив при этом его знак на противоположный, то получим верное неравенство.
Свойство 4.
Доказательство: Пусть 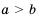
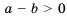

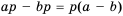
Если 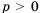
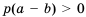
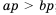
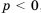
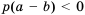
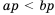
Так как 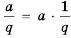
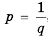
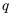
Следствие:
Доказательство: Разделим обе части неравенства 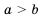
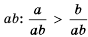
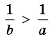
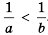
Пример №290
Дано: 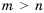
Решение:
1) Если к обеим частям верного неравенства 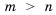
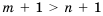
3) Если обе части верного неравенства 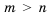
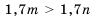
Решение таких упражнений можно записать короче:
6) Если обе части верного неравенства 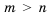
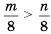
Напомним, что в математике есть и двойные числовые неравенства: 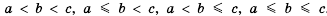
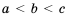
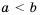
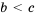
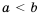
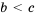
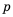
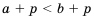
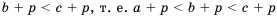
Таким образом, если ко всем частям верного двойного неравенства прибавить одно и то же число, то получим верное двойное неравенство.
Рассуждая аналогично, получаем:
Рассмотренные нами свойства числовых неравенств можно использовать для оценивания значении выражении.
Пример №291
Оценить периметр квадрата со стороной 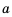
Решение:
Так как периметр 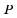
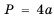
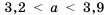
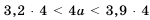
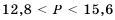
Следовательно, периметр квадрата больше чем 12,8 см, но меньше чем 15,6 см.
Ответ. 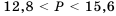
Пример №292
Дано: 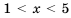
Решение:
Используя форму записи, предложенную в задании 5 примера, получим:
Почленное сложение и умножение неравенств
Продолжим рассмотрение свойств неравенств.
Допустим, имеем два верных неравенства одного знака: 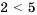
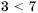
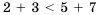
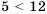
Свойство 5 (почленное сложение неравенств). Если 


Доказательство: К обеим частям неравенства 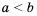
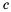
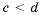
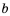
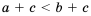
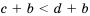
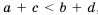
Аналогично доказываем, что если 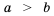
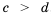
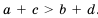
Свойство 5 справедливо и в случае почленного сложения более чем двух неравенств.
Пример №293
Стороны некоторого треугольника равны 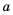
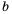
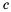
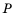
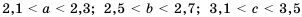
Решение:
Приведем сокращенную запись решения:
Таким образом, 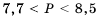
Ответ. 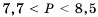
Свойство 6 (почленное умножение неравенств). Если 

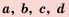

Доказательство: Умножим обе части неравенства 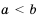
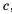
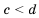
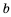
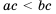
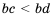
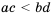
Аналогично можно доказать, что если 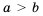
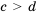
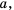
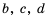
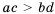
Отметим, что свойство 6 справедливо и для более чем двух неравенств.
Следствие: Если 


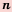
Доказательство: Перемножив почленно 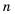
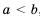
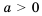
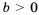
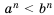
С помощью рассмотренных нами свойств можно оценивать сумму, разность, произведение и частное чисел.
Пример №294
Дано: 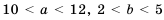
Решение:
1)
2) Чтобы оценить разность 
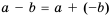
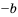
Умножив все части неравенства 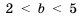
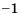
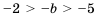
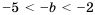
3)
4) Чтобы оценить частное 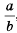
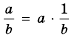
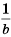
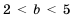
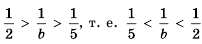
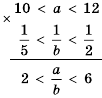
Ответ.
С помощью рассмотренных свойств можно также доказывать неравенства.
Пример №295
Доказать, что 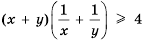
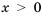
Решение:
К каждому множителю левой части неравенства применим неравенство между средним арифметическим и средним геометрическим (неравенство Коши), получим:
Используя свойство 4, обе части каждого из этих неравенств умножим на 2, получим:
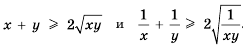
Перемножим эти неравенства почленно:
Таким образом,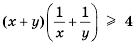
Неравенства с переменными. решение неравенства
Также решениями неравенства 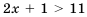
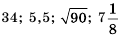
Решением неравенства с одной переменной называют такое значение переменной, которое обращает его в верное числовое неравенство.
Решить неравенство — означает найти все его решения или доказать, что решений нет.
Пример №296
Решить неравенство: 1)
Решение:
1) 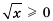
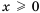
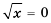
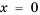
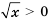
2) 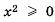
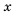
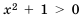
любом 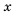
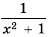
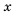
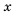
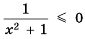
Ответ. 1) Любое число, большее нуля; 2) нет решений.
Числовые промежутки. пересечение и объединение множеств
Множество решений неравенств удобно записывать с помощью числовых промежутков.
Пример №297
Пример №298
Пример №299
Пример №300
Пример №301
Неравенству 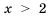
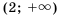
Пример №302
Неравенству 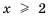
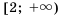
Пример №303
Множество чисел, удовлетворяющих условию 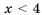
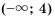
Пример №304
Множество чисел, удовлетворяющих условию 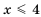
Таким образом, если конец промежутка принадлежит промежутку (например, для нестрогого неравенства), то этот конец заключают в квадратную скобку, во всех остальных случаях конец заключают в круглую скобку.
Множество всех чисел изображает вся координатная прямая и его записывают в виде 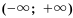
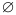
Над множествами можно выполнять некоторые действия (операции). Рассмотрим два из них: пересечение и объединение.
Пересечением множеств 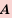
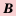
Пересечение множеств записывают с помощью символа 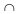
Пример №305
Если даны множества 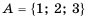
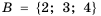
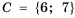
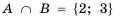
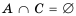
Пересечением числовых промежутков называют множество, которое содержит все числа, принадлежащие как одному промежутку, так и другому.
Пример №306
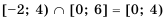
Пример №307
Промежутки 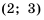
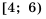
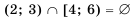
Объединением множеств 

Для записи объединения множеств используют символ 
Пример №308
Если даны множества 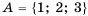
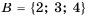
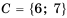
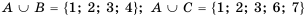
Объединением числовых промежутков называют множество, которое состоит из всех чисел, принадлежащих хотя бы одному из этих промежутков.
Пример №309
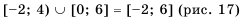
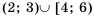
Линейные неравенства с одной переменной. Равносильные неравенства
Неравенства вида 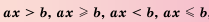


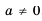
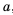
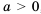
Пример №310
Решить неравенство: 1) 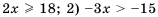
Решение:
1) Разделив обе части неравенства на 2, получим: 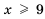
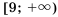
Ответ. 1) 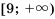
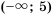
Отметим, что ответ можно было записать и так:
1) 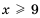
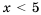
Неравенства, имеющие одни и те же решения, называют равносильными. Неравенства, не имеющие решений, также являются равносильными.
Для неравенств с переменными имеют место свойства, подобные тем, которые справедливы и для уравнений:
Чтобы решить уравнение, мы приводим его к равносильному ему, но более простому уравнению. Аналогично, пользуясь свойствами неравенств, можно решать и неравенства, приводя их к более простым неравенствам, им равносильным.
Пример №311
Решить неравенство
Решение:
Получили неравенство, равносильное исходному. Оно не имеет решений, так как при любом значении 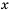
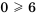
Пример №312
Решить неравенство 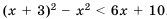
Решение:
Раскрыв скобки, получим:
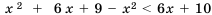
Решая далее, имеем: 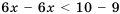
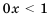
Последнее неравенство равносильно исходному и является верным при любом значении 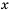
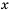
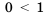
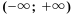
Ответ: 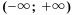
Из примеров 2 и 3 можно сделать вывод, что
неравенства вида 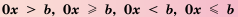
Пример №313
Для каждого значения 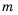
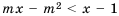
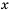
Решение:
Значение выражения 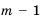
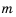
1) Если 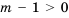
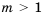
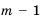
2) Если 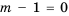
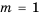
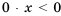
3) Если 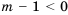
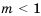

Ответ. Если 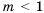
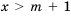
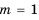
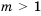
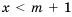
Системы линейных неравенств с одной переменной, их решение
Нам нужно найти такие значения 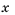
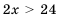
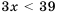
Решив каждое из неравенств системы, имеем систему:
Значит, значение 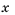
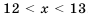
Следовательно, скорость велосипедиста больше чем 12 км/ч, но меньше чем 13 км/ч.
Число 12,6 удовлетворяет каждому из неравенств системы
Решением системы неравенств с одной переменной называют значение переменной, при котором верным является каждое из неравенств системы.
При решении системы неравенств целесообразно придерживаться следующей последовательности действий:
Пример №314
Решить систему неравенств:
Решение:
Постепенно заменяя каждое из неравенств системы ему равносильным, но более простым, получим:
Отметим на координатной прямой множество чисел, удовлетворяющих неравенству 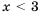
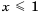
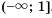
Ответ. 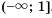
Ответ в примере 1 можно записать и так: 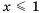
Пример №315
Найти все целые решения системы неравенств:
Решение:
Найдем сначала все решения системы:
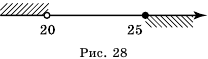
Пример №316
Решить систему неравенств:
Решение:
Отметив полученные решения неравенств системы на координатной прямой (рис. 28), видим, что общих точек у них нет, а значит, пересечением промежутков является пустое множество. Следовательно, система решений не имеет.
Пример №317
Решить неравенство 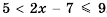
Решение:
Перепишем данное двойное неравенство в виде системы неравенств:
Решим эту систему:
Таким образом, 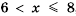
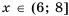
Ответ. 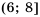
Решение можно записать и так:
А ответ можно также представить в виде: 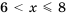
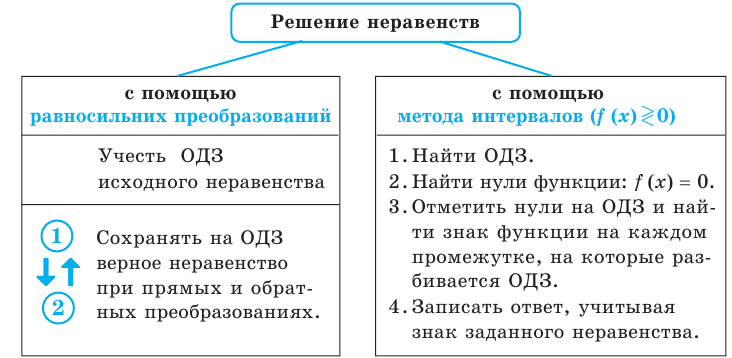
Неравенства: равносильные преобразования неравенств и общий метод интервалов
Понятия неравенства с одной переменной и его решений
Определение:
Если два выражения с переменной соединить одним из знаков 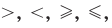
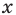
Пример:
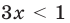
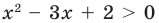
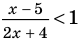
Определение:
Решением неравенства с переменной называется значение переменной, которое обращает заданное неравенство в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет
Пример:
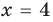
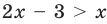
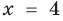
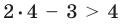
2. Область допустимых значений (ОДЗ)
Определение:
Областью допустимых значений (или областью определения) неравенства называется общая область определения для функций 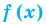
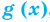
Пример:
Для неравенства 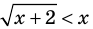
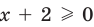
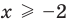
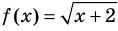
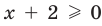
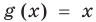
3. Равносильные неравенства
Определение:
Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения
то есть каждое решение первого неравенства является решением второго и наоборот, каждое решение второго неравенства является решением первого
1. Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве)
2. Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не меняя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного неравенства)
3. Если обе части неравенства умножить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства) и изменить знак неравенства на противоположный, то получим неравенство, равносильное заданному (на ОДЗ заданного неравенства)
4. Метод интервалов (решения неравенств вида 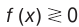
2. Найти нули функции
3. Отметить нули на ОДЗ и найти знак функции 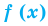
4. Записать ответ, учитывая знак заданного неравенства
Пример:
Решите неравенство
► Пусть
1. ОДЗ: 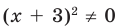
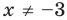
2. Нули функции:
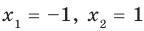
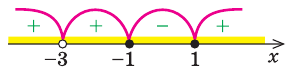
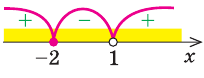
3.
Ответ:
5. Схема поиска решения неравенств



Объяснение и обоснование:
Понятия неравенства с переменной и его решений
Если два выражения с переменной соединить одним из знаков 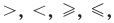
Аналогично уравнению, неравенство с переменной (например, со знаком 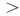
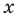
Напомним, что решением неравенства называется значение переменной, которое обращает это неравенство в верное числовое неравенство.
Решить неравенство — значит найти все его решения или доказать, что их нет.
Например, решениями неравенства 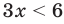
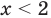
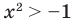
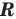
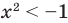
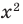
Область допустимых значений (ОДЗ) неравенств
Область допустимых значений (ОДЗ) неравенства определяется аналогично ОДЗ уравнения. Если задано неравенство 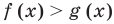
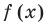
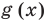
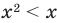
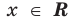
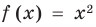
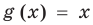
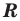
Понятно, что каждое решение заданного неравенства входит как в область определения функции 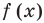
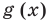
Например, в неравенстве 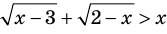
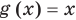
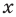
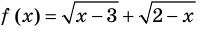
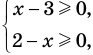
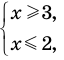
В основном при решении неравенств различных видов приходится применять один из двух методов решения: равносильные преобразования неравенств или так называемый метод интервалов.
Равносильные неравенства
С понятием равносильности неравенств вы знакомы еще из курса алгебры 9 класса. Как и для случая равносильных уравнений, равносильность неравенств мы будем рассматривать на определенном множестве.
Два неравенства называются равносильными на некотором множестве, если на этом множестве они имеют одни и те же решения, то есть каждое решение первого неравенства является решением второго, и наоборот, каждое решение второго неравенства является решением первого.
Договоримся, что в дальнейшем все равносильные преобразования неравенств будем выполнять на ОДЗ заданного неравенства. В случае когда ОДЗ заданного неравенства является множество всех действительных чисел, мы не всегда будем его записывать (как не записывали ОДЗ при решении линейных или квадратных неравенств). И в других случаях главное — не записать ОДЗ при решении неравенства, а действительно учесть ее при выполнении равносильных преобразований заданного неравенства.
Общие ориентиры выполнения равносильных преобразований неравенств аналогичны соответствующим ориентирам выполнения равносильных преобразований уравнений.
Как указывалось выше, выполняя равносильные преобразования неравенств, необходимо учитывать ОДЗ заданного неравенства — это и есть первый ориентир для выполнения равносильных преобразований неравенств.
По определению равносильности неравенств необходимо обеспечить, чтобы каждое решение первого неравенства было решением второго, и наоборот, каждое решение второго неравенства было решением первого. Для этого достаточно обеспечить сохранение верного неравенства на каждом шаге решения не только при прямых, но и при обратных преобразованиях. Это и есть второй ориентир для решения неравенств с помощью равносильных преобразований. Действительно, каждое решение неравенства обращает его в верное числовое неравенство, и если верное неравенство сохраняется, то решение каждого из неравенств будет также и решением другого, таким образом, неравенства будут равносильны (соответствующие ориентиры схематически представлены в пункте 5 табл. 11).
Например, чтобы решить с помощью равносильных преобразований неравенство
достаточно учесть его ОДЗ: 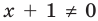
► Данное неравенство равносильно
совокупности двух систем:
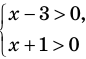
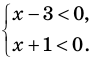
Тогда получаем 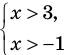
Таким образом, 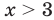
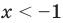
Ответ: 
Заметим, что при записи условия положительности дроби — совокупности систем (2) — мы неявно учли ОДЗ неравенства (1). Действительно, если 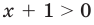
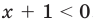
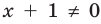
Кроме выделенных общих ориентиров, для выполнения равносильных преобразований неравенств можно также пользоваться специальными теоремами о равносильности. В связи с уточнением определения равносильности неравенств обобщим также формулировки простейших теорем о равносильности неравенств, известных из курса алгебры 9 класса.
1. Если из одной части неравенства перенести в другую часть слагаемые с противоположным знаком, то получим неравенство, равносильное заданному (на любом множестве).
2. Если обе части неравенства умножить или разделить на одно и то же положительное число (или на одну и ту же функцию, которая определена и положительна на ОДЗ заданного неравенства), не изменяя знак неравенства, то получим неравенство, равносильное заданному (на ОДЗ заданного).
3. Если обе части неравенства у множить или разделить на одно и то же отрицательное число (или на одну и ту же функцию, которая определена и отрицательна на ОДЗ заданного неравенства ) и изменить знак неравенства на противоположный, то получим неравенство,равносильное заданному (на ОДЗ заданного).
Обоснование этих теорем полностью аналогично обоснованию ориентиров для равносильных преобразований заданного неравенства.
Замечание. Для обозначения перехода от заданного неравенства к неравенству, равносильному ему, можно применять специальный значок 
Метод интервалов
Решение неравенств методом интервалов опирается на свойства функций, связанные с изменением знаков функции. Объясним эти свойства, используя графики известных нам функций, например функций 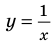
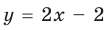
Рассматривая эти графики, замечаем, что функция может изменить свой знак только в двух случаях:
1) если график разрывается (как в случае функции 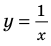
2) если график без разрыва переходит из нижней полуплоскости в верхнюю (или наоборот). Но тогда график пересекает ось 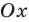
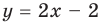
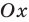
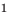
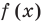
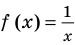
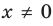
В таблице 12 приведено решение дробно-рационального неравенства 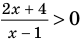
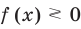
Пример:
Решение:
►
1. ОДЗ: 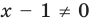
2. Нули
тогда 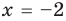
3.
4. Ответ: 
1. Рассмотрим функцию, стоящую в левой части этого неравенства, и обозначим ее через 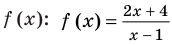
Решением неравенства 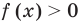
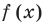
2. Нас интересуют те промежутки области определения функции 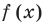
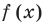
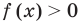
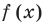
3. Если теперь отметить нули на области определения функции 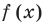
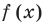
4. Из рисунка видно, что решением неравенства является объединение промежутков
1. Найти ОДЗ неравенства
2. Найти нули
3. Отметить нули на ОДЗ и найти знак функции в каждом промежутке, на которые разбивается ОДЗ
4. Записать ответ, учитывая знак неравенства
Приведем пример решения более сложного дробно-рационального неравенства методом интервалов и с помощью равносильных преобразований.
Пример:
Решите неравенство
I способ (метод интервалов)
Решение:
►Пусть
1. ОДЗ:
2. Нули
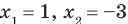
3. Отмечаем нули функции на ОДЗ и находим знак 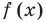
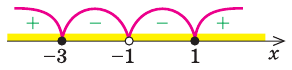
Данное неравенство имеет вид 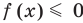
При нахождении нулей 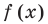
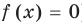
Записывая ответ к нестрогому неравенству, следует учесть, что все нули функции должны войти в ответ (в данном случае — числа 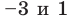
II способ (с помощью равносильных преобразований)
Выберем для решения метод равносильных преобразований неравенства. При выполнении равносильных преобразований мы должны учесть ОДЗ данного неравенства, то есть учесть ограничение 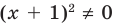
Но если 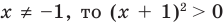
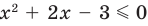
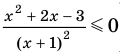
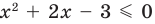
Чтобы решить полученное квадратное неравенство, найдем корни квадратного трехчлена 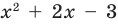
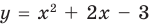
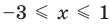
Поскольку все преобразования были равносильными только на ОДЗ, то мы должны выбрать те решения квадратного неравенства, которые удовлетворяют ограничению ОДЗ.
Решение:
► ОДЗ: 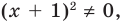
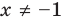
Тогда 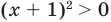
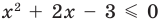
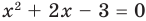
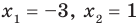
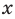
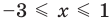
Учитывая ОДЗ, получаем ответ.
Ответ: 
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.