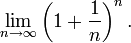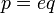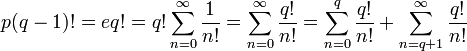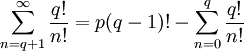Что значит слово следует за числом
Значение слова «число»
1. Понятие, служащее выражением количества, при помощи которого производится счет. Простые числа. Целое число. Положительные числа. Теория чисел (наука о целых числах).
2. День месяца в порядковом ряду других дней. В первых числах августа. □ — То было ровно шесть лет тому, весной, тридцать первого марта, — заметьте число, господа, — накануне… — Первого апреля! — закричал юноша в завитках. Достоевский, Ползунков. — Кто знает, какое сегодня число? Никандров, Седой Каспий.
3. Количество кого-, чего-л. Эти заводы — числом десять — занимают собой площадь в шестьсот тысяч десятин. Мамин-Сибиряк, Сестры. У меня есть одна слабость: мне хочется возможно большее число людей приохотить к писательству. Паустовский, Кара-Бугаз.
4. Состав, ряд, совокупность кого-, чего-л. [Чертокуцкий] служил прежде в одном из кавалерийских полков, был один из числа значительных и видных офицеров. Гоголь, Коляска. Дом ее принадлежал к числу приятнейших в городе. Тургенев, Дворянское гнездо. Я был в числе писателей, встречавших Назыма Хикмета на аэродроме. Сельвинский, Я буду говорить о стихах.
5. Лингв. Грамматическая категория, выражающая морфологическими средствами языка единичность или множественность предметов или лиц. Множественное число. Двойственное число.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ЧИСЛО’, а́, мн. чи́сла, сел, ckам, ср. 1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое ч. Дробное ч. Именованное ч. Простое ч. (см. простой 1 в 1 знач.). Теория чисел (отдел математики, изучающий общие свойства чисел). 2. То же, что цифра в 1 знач. (старин.). 3. Тот или иной день месяца в его порядковом ряду, месте (при названии месяца слово «число» в речи обычно опускается, напр. «первое мая» вм. «первое число мая»). Первого числа (т. е. в первый день месяца) он возвращается из отпуска. Какое сегодня ч.? Какого числа твой день рождения? Пометить письмо задним числом (см. задний), завтрашним, вчерашним числом. Июня третьего числа коляска легкая в дорогу его по почте понесла. Пушкин. В последних числах сентября. в деревне скучно, грязь, ненастье. Пушкин. 4. только ед., кого-чего. Количество (кого-чего-н., считаемого отдельными особями, единицами, штуками). Собралось большое ч. гостей. Ч. книг в библиотеке сильно возросло. Круглым числом (см. круглый в 3 знач.). Хлопочут набирать учителей полки, числом поболее, ценою подешевле. Грибоедов. 5. только ед. Совокупность, ряд известного количества кого-чего-н. А смешивать два эти ремесла есть тьма искусников; я не из их числа. Грибоедов. В числе присутствующих не оказалось ни одного математика. Все дружно принялись за работу, и новички в том числе. 6. Грамматическая категория, показывающая, об одном или о большем числе предметов идет речь (грам.). Единственное ч. Двойственное ч. (указывает на два предмета). Множественное ч. (указывает на число предметов больше одного или, в языках, имеющих формы двойственного числа, — на число предметов больше двух). Изменяться в роде, числе и падеже. ◊
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
число́
1. основное понятие математики, знак, выражающий количество, состоящий из одной или нескольких цифр ◆ Множество целых чисел.
2. о счётных объектах — количество ◆ Число пользователей Интернета растёт с каждым днём.
3. дата, день календарного месяца ◆ Какое сегодня число?
4. лингв. в ряде естественных языков — грамматическая категория имени и глагола, позволяющая выразить единичность или множественность ◆ Глагол здесь стоит в единственном числе.
5. истор. перепись населения (употреблялось во времена первой переписи, проведённой татаро-монголами)
Фразеологизмы и устойчивые сочетания
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова лудильщик (существительное):
Включается ли в период времени дата после предлогов «до» и «по»
Если в договоре для определения срока используется предлог «по», то дата после него включается в соответствующий срок. Эта позиция обусловлена тем, что при толковании условий договора суд принимает во внимание буквальное значение содержащихся в нем слов и выражений ( ч. 1 ст. 401 ГК). А по словарю русского языка С.И. Ожегова предлог «по» имеет несколько значений, в том числе указывает на меру времени или срок. Другими словами, предлог «по» перед датой подразумевает «включая эту дату».
Пример
В договоре указано, что товар должен быть оплачен в срок по 25.01.2021. В таком случае последний день для оплаты товара — 25.01.2021.
Стороны согласовали срок действия договора с 01.01.2021 по 28.02.2021. В этой ситуации последний день действия договора — 28.02.2021.
По поводу предлога «до» отсутствует единое мнение.
Одни считают, что использование предлога «до» исключает указанную после него дату из срока. Например, если указано «до 10.02.2021», то срок оканчивается 09.02.2021 в 24 часа 00 минут. Объясняется это тем, что по словарю русского языка С.И. Ожегова предлог «до» употребляется для указания на время, отделяющее одно событие от другого.
Вместе с тем есть и противоположная точка зрения — предлог «до» не исключает указанную после него дату из срока. Так, если указано «до 10.02.2021», то последний день срока — 10.02.2021. Такой позиции, например, придерживался ВХС в письме от 03.06.2005 N 03-24/1053.
На заметку
В Инструкции по делопроизводству установлено правило касательно предлога «до». Так, если срок исполнения документа определяется с использованием предлога «до», указанная за ним дата является крайней датой исполнения документа (подп. 146.4 п. 146). Однако Инструкция по делопроизводству устанавливает общие требования к документированию управленческой деятельности и организации работы с документами, т.е. не содержит требований к договорам (п. 1).
Следовательно, если в договоре для определения срока использован предлог «до», то может возникнуть спор.
Суд в таком случае будет устанавливать конечную дату срока путем сопоставления условия о сроке с другими условиями и смыслом договора в целом. Если это не поможет определить момент окончания срока, то суд будет выяснять действительную общую волю сторон с учетом цели договора. При этом будут приниматься во внимание все соответствующие обстоятельства, включая предшествующие договору переговоры и переписку, практику, установившуюся во взаимных отношениях сторон, последующее поведение сторон (ст. 401 ГК).
Во избежание споров рекомендуем добавлять слово «включительно» после указания даты. Это целесообразно делать как при использовании предлога «до», так и с предлогом «по». Также избежать разной трактовки срока можно, если использовать конструкцию «не позднее…».
Примеры формулировок в договоре
«Срок оплаты работ — до 10.02.2021 включительно.»
«Срок действия настоящего договора с 01.01.2021 по 20.03.2021 включительно.»
«Товар по настоящему договору должен быть поставлен не позднее 29.01.2021.»
Читайте этот материал в ilex >>*
*по ссылке Вы попадете в платный контент сервиса ilex
Число е
Играет важную роль в дифференциальном и интегральном исчислении, а также многих других разделах математики.

Содержание
Способы определения
Число e может быть определено несколькими способами.
Свойства
История
Данное число иногда называют неперовым в честь шотландского учёного Непера, автора работы «Описание удивительной таблицы логарифмов» (1614 год). Однако это название не совсем корректно, так как у него логарифм числа x был равен 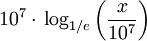
Впервые константа негласно присутствует в приложении к переводу на английский язык вышеупомянутой работы Непера, опубликованному в 1618 году. Негласно, потому что там содержится только таблица натуральных логарифмов, определённых из кинематических соображений, сама же константа не присутствует (см.: Непер).
Предполагается, что автором таблицы был английский математик Отред.
Саму же константу впервые вычислил швейцарский математик Бернулли при анализе следующего предела:
Первое известное использование этой константы, где она обозначалась буквой b, встречается в письмах Лейбница Гюйгенсу, 1690—1691 годы.
Букву e начал использовать Эйлер в 1727 году, а первой публикацией с этой буквой была его работа «Механика, или Наука о движении, изложенная аналитически» 1736 год. Соответственно, e обычно называют числом Эйлера. Хотя впоследствии некоторые учёные использовали букву c, буква e применялась чаще и в наши дни является стандартным обозначением.
Почему была выбрана именно буква e, точно неизвестно. Возможно, это связано с тем, что с неё начинается слово exponential («показательный», «экспоненциальный»). Другое предположение заключается в том, что буквы a, b, c и d уже довольно широко использовались в иных целях, и e была первой «свободной» буквой. Неправдоподобно предположение, что Эйлер выбрал e как первую букву в своей фамилии (нем. Euler ).
Способы запоминания
Доказательство иррациональности
Пускай 
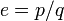
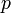
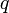
Умножая обе части уравнения на 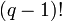
Переносим 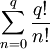
Все слагаемые правой части целые, следовательно:
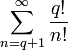
Но с другой стороны
Интересные факты
Примечания
См. также
Ссылки
Числа с собственными именами
Полезное
Смотреть что такое «Число е» в других словарях:
число — Прие моч ное Источник: ГОСТ 111 90: Стекло листовое. Технические условия оригинал документа Смотри также родственные термины: 109. Число бетатронных колебаний … Словарь-справочник терминов нормативно-технической документации
число — сущ., с., употр. очень часто Морфология: (нет) чего? числа, чему? числу, (вижу) что? число, чем? числом, о чём? о числе; мн. что? числа, (нет) чего? чисел, чему? числам, (вижу) что? числа, чем? числами, о чём? о числах математика 1. Числом… … Толковый словарь Дмитриева
ЧИСЛО — ЧИСЛО, числа, мн. числа, чисел, числам, ср. 1. Понятие, служащее выражением количества, то, при помощи чего производится счет предметов и явлений (мат.). Целое число. Дробное число. Именованное число. Простое число. (см. простой1 в 1 знач.).… … Толковый словарь Ушакова
ЧИСЛО — абстрактное, лишенное особенного содержания обозначение какоголибо члена некоторого ряда, в котором этому члену предшествует или следует за ним какой нибудь др. определенный член; абстрактный индивидуальный признак, отличающий одно множество от… … Философская энциклопедия
Число — Число грамматическая категория, выражающая количественные характеристики предметов мысли. Грамматическое число одно из проявлений более обшей языковой категории количества (см. Категория языковая) наряду с лексическим проявлением («лексическое… … Лингвистический энциклопедический словарь
ЧИСЛО e — Число, приближенно равное 2,718, которое часто встречается в математике и естественных науках. Например, при распаде радиоактивного вещества по истечении времени t от исходного количества вещества остается доля, равная e kt, где k число,… … Энциклопедия Кольера
число — а; мн. числа, сел, слам; ср. 1. Единица счёта, выражающая то или иное количество. Дробное, целое, простое ч. Чётное, нечётное ч. Считать круглыми числами (приблизительно, считая целыми единицами или десятками). Натуральное ч. (целое положительное … Энциклопедический словарь
ЧИСЛО — ср. количество, счетом, на вопрос: сколько? и самый знак, выражающий количество, цифра. Без числа; нет числа, без счету, многое множество. Поставь приборы, по числу гостей. Числа римские, арабские или церковные. Целое число, ·противоп. дробь.… … Толковый словарь Даля
ЧИСЛО — ЧИСЛО, а, мн. числа, сел, слам, ср. 1. Основное понятие математики величина, при помощи к рой производится счёт. Целое ч. Дробное ч. Действительное ч. Комплексное ч. Натуральное ч. (целое положительное число). Простое ч. (натуральное число, не… … Толковый словарь Ожегова
ЧИСЛО Е — ЧИСЛО «Е» (ЕХР), иррациональное число, служащее основанием натуральных ЛОГАРИФМОВ. Это действительное десятичное число, бесконечная дробь, равная 2,7182818284590. является пределом выражения (1/ ) при п, стремящемся к бесконечности. По сути,… … Научно-технический энциклопедический словарь
Натуральные числа
Определение натурального числа
Натуральные числа — это числа, которые мы используем для подсчета чего-то конкретного, осязаемого.
Вот какие числа называют натуральными: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13 и т. д.
Натуральный ряд — последовательность всех натуральных чисел, расположенных в порядке возрастания. Первые сто можно посмотреть в таблице.
Какие операции возможны над натуральными числами
Записывайтесь на курсы обучения математике для учеников с 1 по 11 классы!
Десятичная запись натурального числа
В школе мы проходим тему натуральных чисел в 5 классе, но на самом деле многое нам может быть интуитивно понятно и раньше. Проговорим важные правила.
Мы регулярно используем цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. При записи любого натурального числа можно использовать только эти цифры без каких-либо других символов. Записываем цифры одну за другой в строчку слева направо, используем одну высоту.
Примеры правильной записи натуральных чисел: 208, 567, 24, 1 467, 899 112. Эти примеры показывают нам, что последовательность цифр может быть разной и некоторые даже могут повторяться.
077, 0, 004, 0931 — это примеры неправильной записи натуральных чисел, потому что ноль расположен слева. Число не может начинаться с нуля. Это и есть десятичная запись натурального числа.
Количественный смысл натуральных чисел
Натуральные числа несут в себе количественный смысл, то есть выступают в качестве инструмента для нумерации.
Представим, что перед нами банан 🍌. Мы можем записать, что видим 1 банан. При этом натуральное число 1 читается как «один» или «единица».
Но термин «единица» имеет еще одно значение: то, что можно рассмотреть, как единое целое. Элемент множества можно обозначить единицей. Например, любое дерево из множества деревьев — единица, любой листок из множества листков — единица.
Представим, что перед нами 2 банана 🍌🍌. Натуральное число 2 читается как «два». Далее, по аналогии:
| 🍌🍌🍌 | 3 предмета («три») |
| 🍌🍌🍌🍌 | 4 предмета («четыре») |
| 🍌🍌🍌🍌🍌 | 5 предметов («пять») |
| 🍌🍌🍌🍌🍌🍌 | 6 предметов («шесть») |
| 🍌🍌🍌🍌🍌🍌🍌 | 7 предметов («семь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌 | 8 предметов («восемь») |
| 🍌🍌🍌🍌🍌🍌🍌🍌🍌 | 9 предметов («девять») |
Основная функция натурального числа — указать количество предметов.
Если запись числа совпадает с цифрой 0, то его называют «ноль». Напомним, что ноль — не натуральное число, но он может обозначать отсутствие. Ноль предметов значит — ни одного.
Однозначные, двузначные и трехзначные натуральные числа
Однозначное натуральное число — это такое число, в составе которого один знак, одна цифра. Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Двузначные натуральные числа — те, в составе которых два знака, две цифры. Цифры могут повторяться или быть различными. Например: 88, 53, 70.
Если множество предметов состоит из девяти и еще одного, значит, речь идет об 1 десятке («один десяток») предметов. Если один десяток и еще один, значит, перед нами 2 десятка («два десятка») и так далее.
По сути, двузначное число — это набор однозначных чисел, где одно записывается справа, а другое слева. Число слева показывает количество десятков в составе натурального числа, а число справа — количество единиц. Всего двузначных натуральных чисел — 90.
Трехзначные натуральные числа — числа, в составе которых три знака, три цифры. Например: 666, 389, 702.
Одна сотня — это множество, состоящее из десяти десятков. Сотня и еще одна сотня — 2 сотни. Прибавим еще одну сотню — 3 сотни.
Вот как происходит запись трехзначного числа: натуральные числа записываются одно за другим слева направо.
Крайнее правое однозначное число указывает на количество единиц, следующее — на количество десятков, крайнее левое — на количество сотен. Цифра 0 показывает отсутствие единиц или десятков. Поэтому 506 — это 5 сотен, 0 десятков и 6 единиц.
Точно так же определяются четырехзначные, пятизначные, шестизначные и другие натуральные числа.
Многозначные натуральные числа
Многозначные натуральные числа состоят из двух и более знаков.
1 000 — это множество с десятью сотнями, 1 000 000 состоит из тысячи тысяч, а один миллиард — это тысяча миллионов. Тысяча миллионов, только представьте! То есть мы можем рассмотреть любое многозначное натуральное число как набор однозначных натуральных чисел.
Например, 2 873 206 содержит в себе: 6 единиц, 0 десятков, 2 сотни, 3 тысячи, 7 десятков тысяч, 8 сотен тысяч и 2 миллиона.
Сколько всего натуральных чисел?
Однозначных 9, двузначных 90, трехзначных 900 и т.д.
Свойства натуральных чисел
Об особенностях натуральных чисел мы уже знаем. А теперь подробно расскажем про их свойства:
| множество натуральных чисел | бесконечно и начинается с единицы (1) |
| за каждым натуральным числом следует другое | оно больше предыдущего на 1 |
| результат деления натурального числа на единицу (1) | само натуральное число: 5 : 1 = 5 |
| результат деления натурального числа самого на себя | единица (1): 6 : 6 = 1 |
| переместительный закон сложения | от перестановки мест слагаемых сумма не меняется: 4 + 3 = 3 + 4 |
| сочетательный закон сложения | результат сложения нескольких слагаемых не зависит от порядка действий: (2 + 3) + 4 = 2 + (3 + 4) |
| переместительный закон умножения | от перестановки мест множителей произведение не изменится: 4 × 5 = 5 × 4 |
| сочетательный закон умножения | результат произведения множителей не зависит от порядка действий; можно хоть так, хоть эдак: (6 × 7) × 8 = 6 × (7 × 8) |
| распределительный закон умножения относительно сложения | чтобы умножить сумму на число, нужно каждое слагаемое умножить на это число и полученные результаты сложить: 4 × (5 + 6) = 4 × 5 + 4 × 6 |
| распределительный закон умножения относительно вычитания | чтобы умножить разность на число, можно умножить на это число отдельно уменьшаемое и вычитаемое, а затем из первого произведения вычесть второе: 3 × (4 − 5) = 3 × 4 − 3 × 5 |
| распределительный закон деления относительно сложения | чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и сложить полученные результаты: (9 + 8) : 3 = 9 : 3 + 8 : 3 |
| распределительный закон деления относительно вычитания | чтобы разделить разность на число, можно разделить на это число сначала уменьшаемое, а затем вычитаемое, и из первого произведения вычесть второе: (5 − 3) : 2 = 5 : 2 − 3 : 2 |
Разряды натурального числа и значение разряда
Напомним, что от позиции, на которой стоит цифра в записи числа, зависит ее значение. Так, например, 1 123 содержит в себе: 3 единицы, 2 десятка, 1 сотню, 1 тысячу. При этом можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен и 1 служит значением разряда тысяч.
Разряд — это позиция, место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда располагаются старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Вы наверняка заметили, что в учебниках часто ставят небольшие пробелы при записи многозначных чисел. Так делают, чтобы натуральные числа было удобно читать. А еще — чтобы визуально разделить разные классы чисел.
Класс — это группа разрядов, которая содержит в себе три разряда: единицы, десятки и сотни.
Десятичная система счисления
Люди в разные времена использовали разные методы записи чисел. И каждая система счисления имеет свои правила и особенности.
Десятичная система счисления — самая распространенная система счисления, в которой для записи чисел используют десять знаков: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
В десятичной системе значение одной и той же цифры зависит от ее позиции в записи числа. Например, число 555 состоит из трех одинаковых цифр. В этом числе первая слева цифра означает пять сотен, вторая — пять десятков, а третья — пять единиц. Так как значение цифры зависит от ее позиции, десятичную систему счисления называют позиционной.
Вопрос для самопроверки
Сколько натуральных чисел можно отметить на координатном луче между точками с координатами: