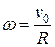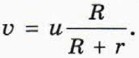Что значит скатывается без проскальзывания

Качение без скольжения

Физика > Качение без скольжения

Качение без скольжения можно распределить на вращательное и поступательное движения.

Задача обучения

Основные пункты

Термины

Если с самого начала объект переворачивается без буксирования, то можно говорить о качении без проскальзывания. Чтобы разобраться, давайте рассмотрим пример с колесом на плоской горизонтальной поверхности.

Движение без проскальзывания понять намного проще, если выделить в нем движение центра масс с линейной скоростью v и вращательное движение вокруг центра с угловой скоростью w.

Движение качения отображает комбинацию вращательного и поступательного движений

Когда объект катится по плоскости без скольжения, точка контакта не смещается. Если представим, что колесо движется со скоростью v, то заметно, что оно должно также совершать движение вокруг своей оси с угловой скоростью ω.

Угловая скорость тела (ω) расположена прямо пропорционально скорости движения. Вы ведь могли заметить: чем быстрее разогналась машина, тем больше оборотов совершают колеса. Чтобы вычислить точную связь между линейной и угловой скоростями, можно взять случай, где колесо смещается на дистанцию х при повороте на углу θ.

Тело, скатывающееся на дистанцию х на плоскости, лишенной скольжения

В математике длина дуги приравнивается к углу сегмента, умноженному на радиус объекта (R). Отсюда выходит, что длина дуги колеса, повернутого на θ, достигает Rθ. Так как колесо постоянно контактирует с поверхностью, длина дуги также равна х. Выходит:

Не забывайте, что х и θ зависят от времени, поэтому возьмем их производные:

Здесь аналогичен v в линейной скорости, а – угловой скорости ω. Теперь можно все упростить:

Источник

Катящееся колесо

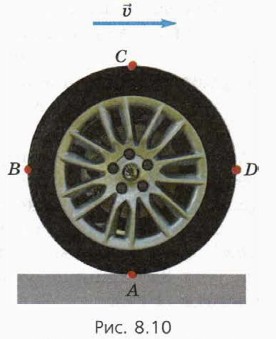
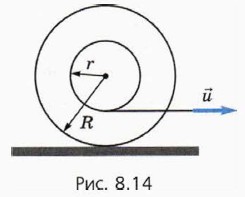
Рассмотрим движение различных точек колеса автомобиля.

Пусть автомобиль едет со скоростью (рис. 8.10), причём его колёса катятся без проскальзывания.

Что означают слова «без проскальзывания»? Это значит, что нижняя точка колеса А покоится относительно земли (при этом шины оставляют чёткие следы). Этот факт — отправная точка для нахождения скорости всех других точек колеса — например, точек В, С, D на рисунке 8.10.

Чтобы найти скорость этих точек, удобно перейти в систему отсчёта, связанную с автомобилем, а потом вернуться в систему отсчёта, связанную с дорогой.

В системе отсчёта, связанной с автомобилем, все точки обода колеса движутся по окружности с равными по модулю скоростями. Обозначим υ_вр модуль этой скорости, обусловленной вращением колеса вокруг своей оси. Выясним: как связаны скорость автомобиля и и скорость вращения υ_вр точек его колеса? Именно тут нам и поможет тот факт, что нижняя точка колеса А покоится относительно земли.

Заметим, что скорость _Авр вращения нижней точки А направлена противоположно скорости автомобиля (рис. 8.11).

_А = _Авр + .

Итак, скорости _Авр и направлены противоположно, а их сумма _А = 0. Следовательно,

то есть скорость движения точек обода колеса в системе отсчёта, связанной с автомобилем, равна по модулю скорости автомобиля.

15. Докажите, что скорость точки С (см. рис. 8.10) относительно дороги равна 2υ.

16. Найдите направление и модуль скорости точек В и D (см. рис. 8.10) относительно земли.

17. Катушка с ниткой (рис. 8.12) может катиться по горизонтальному столу без проскальзывания. Конец нити тянут в горизонтальном направлении со скоростью, равной по модулю u (рис. 8.13). Внутренний радиус катушки r, а внешний R. Докажите, что катушка будет двигаться вправо со скоростью

П о д с к а з к а. Рассмотрите движение точки А, воспользовавшись сложением скоростей, а также тем фактом, что точка катушки, касающаяся стола, покоится относительно стола.

18. С какой скоростью υ и в каком направлении будет двигаться катушка в случае, изображённом на рисунке 8.14?

Если вы выполнили это задание правильно, ответ может показаться вам неправдоподобным. Попробуйте проверить его на опыте, проследив за тем, чтобы катушка катилась без проскальзывания.

19. С какой скоростью едет велосипедист, если сорвавшаяся с колеса в точке А (рис. 8.15) капелька попала снова в эту же точку? Радиус колеса 30 см.

П о д с к а з к а. Перейдите в систему отсчёта, связанную с велосипедистом.

Источник

Скатывание тел с наклонной плоскости

С тем, чтобы проиллюстрировать применение законов динамики твёрдого тела, решим задачу о скатывании цилиндра с наклонной плоскости (рис. 10.5).

Сплошной цилиндр массы m и радиуса R скатывается без проскальзывания с наклонной плоскости. Угол наклона плоскости — a, а высота Н (Н » R). Начальная скорость цилиндра равна нулю. Определим время скатывания — Т и скорость центра масс цилиндра у основания наклонной плоскости.

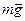
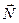
При качении цилиндра на него действуют три силы: сила тяжести , упругая сила реакции опоры и сила трения покоя (ведь качение без проскальзывания!).

Представим это движение суммой двух движений: поступательного со скоростью V_C, с которой движется ось цилиндра, и вращательного вокруг оси цилиндра с угловой скоростью w.

. (10.9)

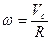
Эта связь скоростей поступательного и вращательного движений следует из условия «движение без проскальзывания».

Продифференцировав уравнение (10.9) по времени, получим соотношение углового и линейного ускорений цилиндра:

, то есть .

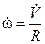
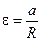
Воспользовавшись теоремой о движении точки центра масс, опишем поступательное движение цилиндра:

. (10.10)

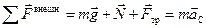
Для описания вращения воспользуемся основным уравнением динамики вращательного движения:

Спроецировав уравнение (10.10) на направления осей x и y, получим два скалярных уравнения:

Обратимся теперь к уравнению (10.11). Из трёх названных сил момент относительно оси цилиндра создаёт только сила трения:

.

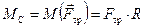
Момент инерции сплошного цилиндра относительно его оси равен (см. лекцию №9):

.

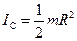
Учитывая всё это, уравнение (10.11) перепишем так:

. (10.14)

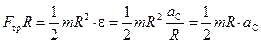
Решая совместно уравнения (10.12) и (10.14), получим следующие значения неизвестных величин:

; (10.15)

. (10.16)

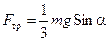
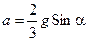
Из уравнения (10.15) следует, что с увеличением угла наклона a должна возрастать и сила трения покоя F_тр. Но, как известно, её рост ограничен предельным значением:

. (10.17)

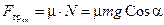
Так как сила трения покоя (10.15) не может превышать предельного значения (10.17), то должно выполняться неравенство:

Отсюда следует, что скатывание будет происходить без проскальзывания до тех пор, пока угол a не превзойдёт значения a_пред:

Здесь m — коэффициент трения цилиндра по плоскости.

Линейное ускорение цилиндра (10.16) величина неизменная, следовательно, поступательное движение цилиндра равноускоренное. При таком движении без начальной скорости цилиндр достигнет основания наклонной плоскости за время:

.

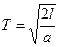
Здесь: l = 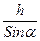— длина плоскости;

a =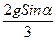, (см.10.16).

Значит, время скатывания:

. (10.18)

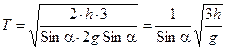
Вычислим конечную скорость поступательного движения оси цилиндра:

. (10.19)

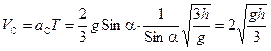
Заметим, что эту задачу можно решить проще, воспользовавшись законом сохранения механической энергии.

В системе, правда, присутствует сила трения, но её работа равна нулю, поскольку точка приложения этой силы в процессе спуска остаётся неподвижной: ведь движение происходит без проскальзывания. Раз нет работы силы трения, механическая энергия системы не меняется.

Рассмотрим энергию цилиндра в начальный момент — на высоте h и в конце спуска. Полная энергия цилиндра в этих положениях одинакова:

.

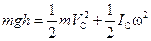
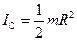
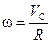
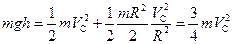
Вспомним, что и . Тогда уравнение закона сохранения энергии можно переписать так:

.

Отсюда легко найдём конечную скорость цилиндра:

,

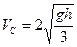
которая блестяще подтверждает полученный нами ранее результат (10.19).

Лекция 11 «Элементы механики жидкости»

1. Давление жидкости. Законы гидростатики.

2. Стационарное течение жидкости. Уравнение неразрывности потока.

3. Основной закон динамики для идеальной жидкости. Уравнение Бернулли.

4. Применение уравнения Бернулли для решения задач гидродинамики.

Источник

Учебники

Журнал «Квант»

Общие

§3. Криволинейное движение. Плоскопараллельное движение твердого тела

3.6 Плоскопараллельное движение

Движение твердого тела называется плоскопараллельным, если траектории движения всех его точек являются плоскими кривыми, лежащими в параллельных плоскостях.

Плоскопараллельное движение твердого тела можно представить как суперпозицию поступательного движения и вращения вокруг оси, направление которой не изменяется. Наглядными примерами такого движения являются качение колеса, движение книги без отрыва от стола и т.д.

Для описания положения абсолютно твердого тела при плоскопараллельном движении необходимо задать две декартовые координаты какой-либо точки тела [1] и угол его поворота, то есть плоскопараллельное движение обладает тремя степенями свободы.

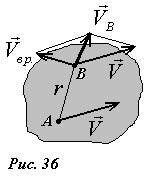
Выберем внутри тела две точки A, B; зададим координаты x_A, y_A точки A и угол φ, который образует отрезок AB с направлением оси X. Три числа x_A, y_A и φ однозначно определяют положение тела на плоскости, следовательно, являются его координатами. Зная эти координаты, можно определить положение в пространстве любой другой точки твердого тела путем геометрических построений.

Покажем теперь, как можно найти скорость любой точки твердого тела при плоскопараллельном движении (рис. 36).

причем вектор скорости вращательного движения направлен перпендикулярно отрезку AB и равен по абсолютной величине V_BP = ωr, где r расстояние от точки B до оси вращения.

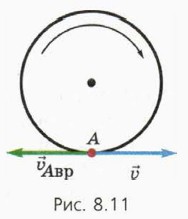
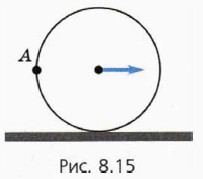
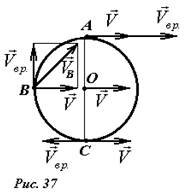
Рассмотрим катящееся без проскальзывания колесо радиуса R (рис. 37).

Пусть его центр движется со скоростью \(

\vec V\). Найдем скорости некоторых других точек колеса. Для этого представим движение колеса как сумму поступательного движения его центра и вращения вокруг его оси. Так как движение происходит без проскальзывания, то угловая скорость вращения определяется формулой \(

\omega = \frac<\upsilon>\). Для точек, находящихся на ободе колеса линейная скорость вращательного движения равна по модулю скорости поступательного движения, так как для них расстояние до оси вращения равно радиусу колеса, поэтому \(

Так как разложение движения на составляющие не является однозначным, можно теперь представить качение колеса как сумму движения точки C и вращения вокруг оси, проходящей через эту точку. Мы показали, что скорость точки C равна нулю, поэтому появляется возможность рассматривать движение колеса как чистый поворот вокруг точки C. Правда, это возможно в течение только бесконечно малого промежутка времени, потому, что в следующий момент точкой касания будет другая точка колеса. Множество точек твердого тела, скорости которых в данный момент равны нулю, образуют мгновенную ось вращения тела. Такая ось существует при любом движении твердого тела. Правда положение этой оси постоянно изменяется, поэтому для вычисления координат точек такое представление движения не дает особых преимуществ. Но для вычисления скоростей точек, рассматривать плоскопараллельное движение как чистый поворот очень удобно.

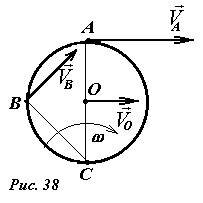
Рассмотренная задача об определении скоростей точек катящегося колеса может быть легко решена, если рассматривать его движение как поворот вокруг точки C (рис. 38): точка A находится на расстоянии 2R от мгновенной оси вращения, поэтому ее скорость равна V_A = 2Rω = 2V; точка B находится на расстоянии \(

R \sqrt<2>\) от оси, ее скорость \(

V \sqrt<2>\). Направления векторов скоростей также совпадают с полученными ранее.

Источник

Вращение абсолютно твердого тела

Если хотя бы две точки абсолютно твердого тела при его вращении остаются неподвижными, то такое вращение называется вращением тела вокруг неподвижной оси. Все точки, лежащие на этой оси и принадлежащие телу также будут неподвижными.

Каждая точка вращающегося твердого тела, не принадлежащая оси, движется по окружности, центр которой находится на оси вращения.

Угол, на который поворачивается каждая точка тела, не лежащая на оси, называется углом поворота. Поэтому угол поворота j аналогичен угловому перемещению точки (рис. 2.8.1).

Так же как и для движения материальной точки по окружности вводятся определения и соответствующие им формулы угловой скорости w и углового ускорения e (см. 2.6.3 и 2.6.12). Скорость любой точки вращающегося тела, находящейся на расстоянии r от оси вычисляется по формуле: 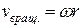. Ускорение произвольной точки тела выражается как сумма нормального и тангенциального ускорений: a = a_n + a_t.

Механическое движение абсолютно твердого тела, при котором только одна из его точек остается неподвижной, называется вращением тела вокруг неподвижной точки.

Ось вращения, проходящая через неподвижную точку перпендикулярно плоскости вращения, называется мгновенной осью вращения.

В качестве примера такого вращения рассмотрим качение колеса без проскальзывания (см. рис. 2.8.2).

Качение без проскальзывания означает, что за время Dt, за которое центр колеса смещается на расстояние Ds, любая точка обода колеса описывает дугу, длина которой равна Ds.

Докажем, что при качении без проскальзывания скорость вращательного движения любой точки колеса равна скорости поступательного движения центра колеса:

. (2.8.1)

, где T – период вращения колеса, R – его радиус. При равномерном движении колеса его центр за время t = T пройдет путь . По определению качения без проскальзывания , Тогда , Þ .

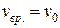
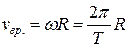
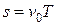
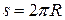
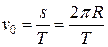
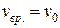
Скорость произвольной точки M, находящейся на ободе колеса, относительно земли равна

, (2.8.3)

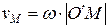
где , так как колесо движется без проскальзывания.

Источник