Что значит скалярная величина
Скалярная величина
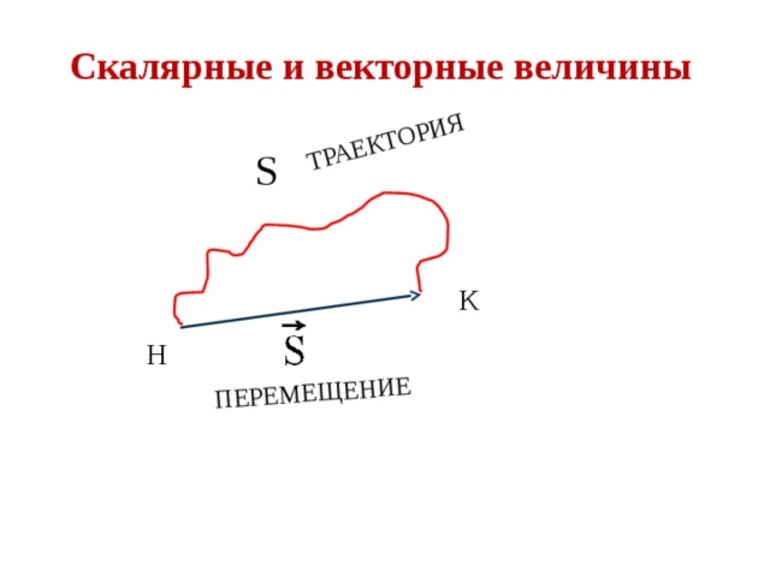
Скалярная величина (от лат. scalaris — ступенчатый) в физике — величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только своим значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д. [1]
Примечания
Полезное
Смотреть что такое «Скалярная величина» в других словарях:
скалярная величина — скаляр Словарь русских синонимов … Словарь синонимов
скалярная величина — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN scalar quantityscalar … Справочник технического переводчика
скалярная величина — skaliarinis dydis statusas T sritis automatika atitikmenys: angl. scalar; scalar quantity vok. skalare Größe, f rus. скалярная величина, f pranc. grandeur scalaire, f … Automatikos terminų žodynas
скалярная величина — skaliarinis dydis statusas T sritis fizika atitikmenys: angl. scalar quantity vok. skalare Größe, f rus. скалярная величина, f pranc. grandeur scalaire, f … Fizikos terminų žodynas
скалярная величина — Syn: скаляр … Тезаурус русской деловой лексики
скалярная проводимость — удельная электрическая проводимость; скалярная проводимость; проводимость Скалярная величина, характеризующая электропроводность среды и являющаяся функцией термодинамических параметров … Политехнический терминологический толковый словарь
колеблющаяся величина — Поочередно возрастающая и убывающая во времени скалярная величина, связанная с описанием и движением механической системы. Примечание В описание механической системы могут входить и силы, действующие в ней. [Сборник рекомендуемых терминов. Выпуск … Справочник технического переводчика
колеблющаяся величина — Поочередно возрастающая и убывающая во времени скалярная величина, связанная с описанием и движением механической системы … Политехнический терминологический толковый словарь
Физическая величина — Эта статья или раздел нуждается в переработке. Пожалуйста, улучшите статью в соответствии с правилами написания статей. Физическая … Википедия
Действие (физическая величина) — У этого термина существуют и другие значения, см. Действие (физика). Действие Размерность L2MT−1 Действие в физике скалярная физическая величина, являющаяс … Википедия
Скалярные и векторные величины в физике и математике
Особенности скалярных величин
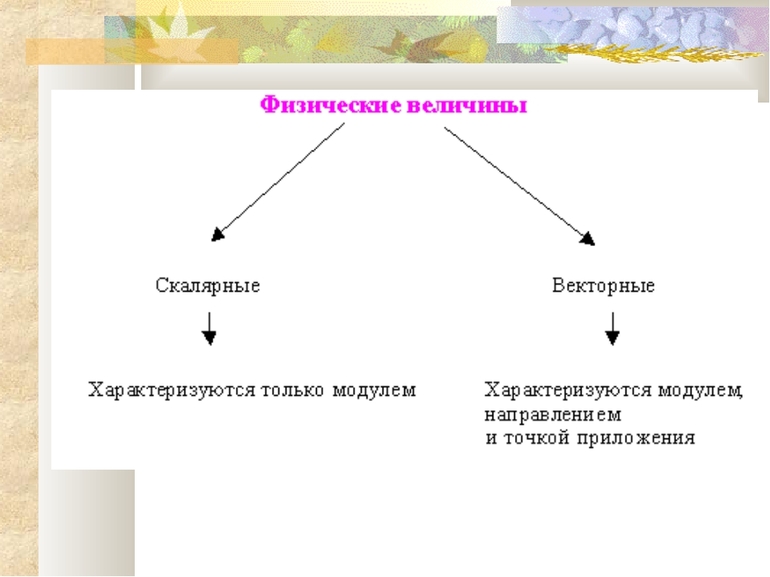
Скалярные величины характеризуются только одним параметром — числовым значением. Они разделяются на 2 вида:
В физике в список скалярных величин входят:
Если скаляры выражают одно единственное свойство физического тела, то они называются однородными. Величины, описывающие несколько свойств объекта, именуются разнородными. Однородные скаляры сравнимы: они либо равны, либо одна из них больше или меньше другой. Но скалярные величины разного рода не могут сравниваться друг с другом.
Определение положительного скаляра и его измерения
Понятие положительной скалярной величины и ее измерения позволяет сравнивать между собой однородные скаляры. Положительная скалярная величина способна принимать значения строго выше 0. Она обозначается знаком «+». Если величина может принимать значения меньше 0, то она называется отрицательной и обозначается символом «-«. Большинство скаляров могут быть только положительными. Для их расчета используют единицы измерения — фиксированного размера объекта.
Чтобы получить скалярную величину, достаточно умножить ее числовое значение на ее единицу измерения. Для структуризации и стандартизации вычислений физических параметров тела была разработана Международная система СИ. Она устанавливает единицы измерения для каждой величины. Во время проведения расчетов скалярных величин применяют алгебраические действия — сложение, вычитание, деление и умножение (отдельный подвид — возведение в степень).
Особенности векторных величин
Их определение: «В физике векторными величинами называются свойства материи, характеризующиеся несколькими параметрами: модулем и направлением». Модулем вектора будет являться числовое значение величины, никогда не принимающее отрицательных значений. Он обозначается символом «||». Для обозначения направления используется стрелка, располагающаяся над символом вектора.
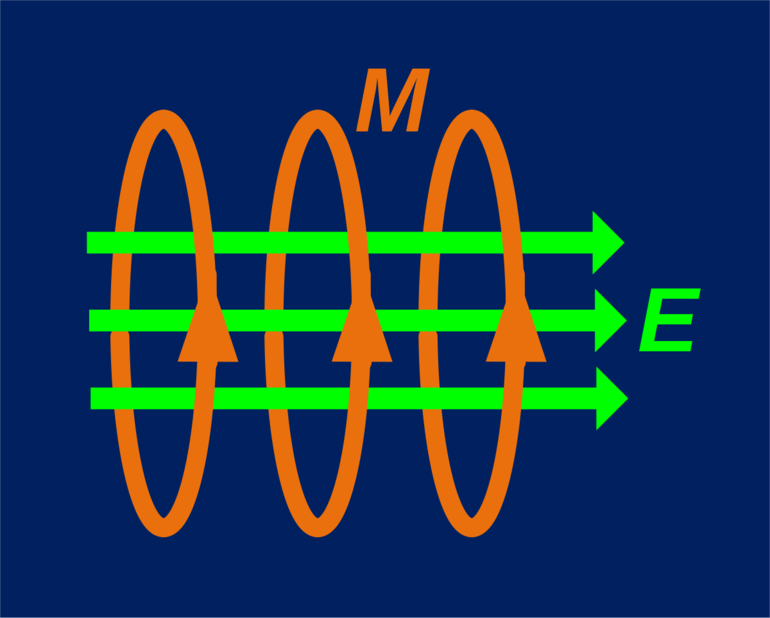
В физике и математике примерами векторных величин являются:
На графиках функции векторные величины изображаются в виде прямой линии, имеющей направление и свои собственные координаты в заданном масштабе.
Свойства векторов
Вектор — математический элемент, представляющий собой прямой отрезок с направлением. Он обозначается либо 2 заглавными латинскими буквами, либо одной прописной. Длиной вектора является его модуль. Если длина вектора равняется 0, то он называется нулевым. Вектор, имеющий длину 1 см, именуется единичным. Длина ненулевого вектора выражается в виде расстояния между началом и концом направленного отрезка. Проекцией вектора на ось является строго положительный отрезок, сонаправленный с исходной осью. Свойства проекции:
Коллинеарные векторы — отрезки, располагающиеся либо на одной прямой, либо на параллельных прямых. Нулевой вектор коллинеарен всегда. Если коллинеарные векторы направлены в одну сторону, то они называются сонаправленными. Если отрезки направлены в диаметрально противоположные стороны, то они называются противоположно направленными. Коллинеарные векторы являются равными, если они одинаковы по модулю и направлению.
Построение отрезков с направлением на плоскости осуществляется при помощи его координат для осей абсцисса и ордината. Для изображения направленного отрезка необходимо построить точки, координаты которых соответствуют началу и концу вектора, и соединить их.
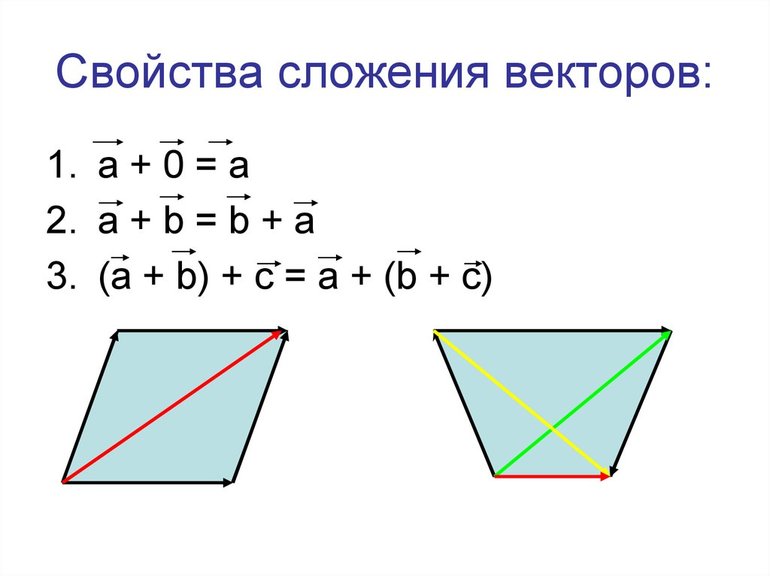
С векторами также можно производить операции сложения, деления, вычитания и умножения. Чтобы сложить два вектора, необходимо от произвольной точки на плоскости отложить первый направленный отрезок и от него отложить второй вектор. Отрезок, соединяющий начало первого вектора и конец второго, будет считаться их суммой. Этот способ сложения именуется методом треугольника.
Вторым способом нахождения суммы векторов является метод параллелограмма. От произвольной точки откладываются оба направленных отрезка. Полученный рисунок нужно достроить до параллелограмма. Диагональ фигуры будет являться суммой векторов.
Для осуществления вычитания необходимо отложить от произвольной точки первый вектор. От полученного отрезка откладывается следующий вектор. Второй отрезок нужно направить в противоположную сторону. Линия, соединяющая отрезки, будет являться разностью векторов.
С векторами также можно проводить операцию умножения. Произведение длин направленных отрезков на косинус угла между ними называется скалярным. В результате вычислений получается число — скаляр. Скалярное произведение равно 0 в случае, когда отрезки пересекаются под углом 90°. Зная скалярное произведение, человек сможет найти косинус угла между построенными векторами.
Полученные в результате выполнения алгебраических операций выражения применяются для исследования перемещения тел вокруг оси вращения и изучения элементов высшей математики. Также направленные отрезки нашли широкое применение в геометрии и астрономии.
Скаляр
Скаляр (от лат. scalaris — ступенчатый) — величина (возможно переменная, то есть функция), каждое значение которой может быть выражено одним числом (чаще всего подразумевается вещественное число).
При смене системы координат скаляр остаётся неизменным (инвариантным), в отличие, например, от компонентов вектора, которые могут быть разными у одного и того же вектора в разных системах координат.
Содержание
Примеры
Важно заметить, что понятие скаляра довольно сильно связано с контекстом. Так, в общепринятом контексте современной физики часть приведённых величин скалярными не являются. [1]
Ошибочные примеры
То же касается координаты тензора любой другой валентности (кроме нулевой).
Ещё одним примером величины, не являющейся, строго говоря, скаляром, является псевдоскаляр (хотя на практике иногда, исходя из соображений удобства или краткости, разграничения между скалярами и псевдоскалярами могут и не проводить, если это не существенно для изложения).
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Скаляр» в других словарях:
скаляр — а, м. scalaire <лат. scalaris ступенчатый < scalae лестница. Величина, в противоположность вектору, определяемая числовым значением без указания направления. БАС 1. Скалярный ая, ое. Скалярные величины. Уш. 1940: Лекс. СИС 1937: скаля/ры;… … Исторический словарь галлицизмов русского языка
скаляр — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] скаляр Величина, каждое значение которой может быть выражено одним (как правило, действительным) числом; по… … Справочник технического переводчика
СКАЛЯР — (от латинского scalaris ступенчатый) (скалярная величина), величина, каждое значение которой (в отличие от вектора) может быть выражено одним (действительным) числом, вследствие чего совокупность значений скаляра можно изобразить на линейной… … Современная энциклопедия
СКАЛЯР — (от лат. scalaris ступенчатый) (скалярная величина) величина, каждое значение которой (в отличие от вектора) может быть выражено одним (действительным) числом, вследствие чего совокупность значений скаляра можно изобразить на линейной шкале… … Большой Энциклопедический словарь
СКАЛЯР — СКАЛЯР, математическое число, имеющее только величину, в отличие от ВЕКТОРА, который имеет еще и направление. Масса и энергия являются скалярными величинами, тогда как вес и сила представлены векторными величинами … Научно-технический энциклопедический словарь
СКАЛЯР — величина, значение которой характеризуется действительным числом (без учета направления). Напр., температура, концентрация и т.п. Геологический словарь: в 2 х томах. М.: Недра. Под редакцией К. Н. Паффенгольца и др.. 1978 … Геологическая энциклопедия
Скаляр — [scalar] величина, каждое значение которой может быть выражено одним (как правило, действительным) числом; по отношению к вектору, который можно рассматривать как многомерную величину, С. величина одномерная. Скалярная (числовая) функция одной… … Экономико-математический словарь
СКАЛЯР — величина, каждое значение которой может быть выражено одним действительным числом без учёта направления млн. другой какой либо оценки в выбранной системе единиц, напр. длина, площадь, объём, плотность, работа, температура и др … Большая политехническая энциклопедия
скаляр — а; м. [лат. scalaris ступенчатый] Матем. Величина, имеющая только числовое значение. ◁ Скалярный, ая, ое. С ые величины. * * * скаляр (от лат. scalaris ступенчатый) (скалярная величина), величина, каждое значение которой (в отличие от вектора)… … Энциклопедический словарь
Разница между векторной и скалярной величиной
В физике выделяют 2 категории величин — векторные и скалярные. Что представляют собой те и другие?
Что представляет собой векторная величина?
Под векторной принято понимать величину, имеющую 2 основные характеристики:
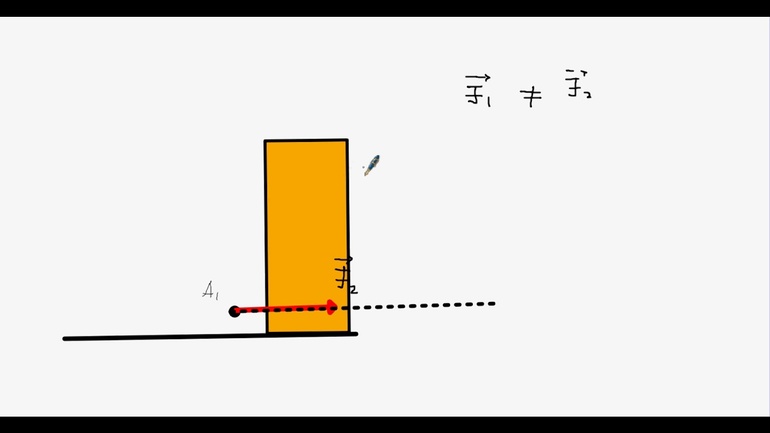
Так, два вектора признаются равными, если модули, а также направления обоих совпадают. Записывается рассматриваемая величина чаще всего как буква, над которой прорисовывается стрелка.
В числе самых распространенных величин соответствующего типа — скорость, сила, а также, например, ускорение.
С геометрической точки зрения вектор может представлять собой направленный отрезок, длина которого соотносится с его модулем.
Если рассматривать векторную величину обособленно от направления, то ее принципиально можно измерить. Правда, это будет, так или иначе, частичная характеристика соответствующей величины. Полная — достигается только в случае ее дополнения параметрами направленного отрезка.
Что представляет собой скалярная величина?
Под скалярной принято понимать величину, которая имеет только 1 характеристику, а именно — численное значение. При этом рассматриваемая величина может принимать положительное или же отрицательное значение.
К распространенным скалярным величинам можно отнести массу, частоту, напряжение, температуру. С ними возможно производить различные математические действия — сложение, вычитание, умножение, деление.
Направление (как характеристика) не свойственно для скалярных величин.
Сравнение
Главное отличие векторной величины от скалярной заключается в том, что у первой ключевые характеристики — модуль и направление, у второй — численное значение. Стоит отметить, что векторную величину, как и скалярную, принципиально можно измерить, правда, в этом случае ее характеристики определятся только частично, поскольку будет недоставать направления.
Определив,в чем разница между векторной и скалярной величиной, отразим выводы в небольшой таблице.
Понятие измерения величины. Свойства скалярных величин.
Понятие измерения величины. Свойства скалярных величин.
Величина – неопределяемое понятие.
(Мы понимаем так: величина – это размер. Аристотель писал: «То или иное количество есть множество, если его можно счесть; есть величина, если его можно измерить».)
Под величиной понимают особые свойства реальных объектов или явлений.
-Какие величины вы знаете? (дл, масса, емкость…)
-Какие тройки взаимосвязанных величин? (ск, вр, рас)
-Каким методом пользуется учитель в нач. школе при ознакомлении с величинами (длиной)? (практическим)
Длина – это свойство предметов иметь протяжённость.
Масса – с математической точки зрения это такая положительная величина, которая обладает свойствами:
масса одинакова у тел, уравновешивающих друг друга на весах;
масса складывается, если тела соединяются вместе.
-Какие бывают величины?
(Разнородные величины- величины, которые выражают разные свойства объектов.
-Какие ещё бывают величины? (в геометрии векторная, скалярная; положительная, отрицательная; переменная, постоянная).
-Какие величины называются скалярными?
(Скалярные величины – величины, не имеющие направления или которые определяются одним численным значением.)
-Назовите свойства скалярных величин.
Свойства однородных скалярных величин
Любые две однородные величины сравнимы : они либо равны, либо одна меньше другой.
Т.е. для любых величин a и b справедливо одно и только одно из отношений:
Например, длина гипотенузы больше длины катета; масса яблока меньше массы арбуза, длины противоположных сторон прямоугольника равны.
Т.е. для любых величин a и b однозначно определяется величина
Например: пусть а- длина отрезка АВ, в – длина отрезка ВС. Тогда длина отрезка АС равна сумме длин отрезков АВ и ВС.
3. Величину можно умножать на неотрицательное действительное число, получая в результате число того же рода.
Например: если длину а отрезка АВ умножить на х=2, то получим длину 2а нового отрезка АС.
Например: Пусть а – длина отрезка АС, в – длина отрезка АВ, тогда длина ВС есть разность длин АС и АВ.
5. Величины одного рода делят, определяя частное через произведение величины на число:
Частным величин а и в называется такое неотрицательное действительное число х, что
Понятие измерения величины. Свойства скалярных величин.
Определение: Измерить величину значит сравнить её с некоторой величиной того же рода, принятой за единицу.
Определение: Если дана величина а и выбрана единица величины е, то в результате измерения величины а находят такое действительное число х, что а = x ● е.
Число x называют численным значением величины а при единице величины е.
Например, 8 кг = 8 1 кг.
Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой.
Выразить 1/5 часа в минутах.
1/5 ч = 1/5 ● 1 ч = 1/5 ● 60 мин = 60/5 мин = 12 мин.
Измерение величин позволяет свести сравнение их к сравнению чисел; операции над величинами к операциям над числами.
Не следует смешивать длину (она одна для отрезка) с численным значением длины, оно различно в зависимости от единицы измерения.
АВ = 4 см = 40 мм = 0,4 м
Свойства скалярных величин
Если величины а и в измерены при помощи единицы величины е, то отношения между величинами а и в будут такими же, как и отношения между их численными значениями и наоборот:
Пример: Сравните: 8 кг и 6 кг
Если величины а и в измерены при помощи единицы величины е, то чтобы найти численное значение суммы а + в , достаточно сложить численные значения величин а и в :
а +в = 3 m + 7 m = (3 + 7) m = 10 m
Например, а = 5 км, b в 3 раза больше длины а, то есть
b = 3 ● а = 3 ● (5 км) = (3● 5) км = 15 км
В начальном курсе математики, в частности в системе Л.В. Занкова, операции над величинами выполняются параллельно с операциями над их численными значениями. Например, в теме «Сложение отрезков» результат сложения можно найти 2 способами.
а =5см, в = 4 см. найти а+в.
Первый способ заключается в том, что строится отрезок = 5см и подстраивается 4 см. Получится всего 9 см.
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-1047428
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
В Госдуме проверят содержание учебников русского языка как иностранного
Время чтения: 2 минуты
Школьников Улан-Удэ перевели на удаленку из-за гриппа и ОРВИ
Время чтения: 1 минута
В МГУ заработала университетская квантовая сеть
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.