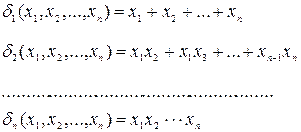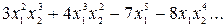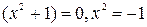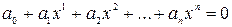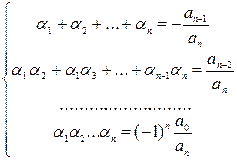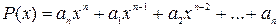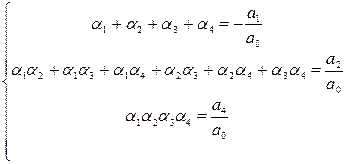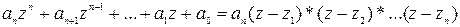Что значит симметрический многочлен
Симметрические многочлены
Многочлен 


Примером симметрических многочленов являются элементарные симметрические многочлены:
Пример 1
.
Пример 2
.
Симметрические многочлены вида

Степенные суммы связаны с элементарными симметрическими многочленами формулами Ньютона:
Эти формулы позволяют последовательно выражать элементарные симметрические многочлены через степенные суммы и наоборот.
Пример 3 При
первая формула такова:
.
Выразим отсюда 




Таким образом, мы можем последовательно выразить и остальные 
Все мы знаем теорему Виета о корнях квадратного трехчлена: если квадратный трехчлен 




Теорема Виета имеет место и для многочлена 

Отметим, что сумма, произведение симметрических многочленов есть опять симметрический многочлен, то есть множество симметрических многочленов замкнуто относительно операций сложения и умножения. Справедлива основная теорема о симметрических многочленах.
Заметка Каждый симметрический многочлен однозначно представим в виде многочлена от элементарных симметрических многочленов.
В заключении рассмотрим следующие примеры:
Пример 4 Разложить многочлен
на множители.
Данный нам многочлен – симметрический относительно своих переменных. Будем считать, что это многочлен третьей степени относительно 



Согласно следствию теоремы Безу, исходный многочлен должен без остатка поделиться на 


Если раскрыть скобки в частном и привести подобные члены:
и искомое разложение будет таким:

Пример 5 Разложить многочлен
на множители, используя формулы Ньютона.
Воспользуемся обозначениями элементарных симметрических многочленов и степенных сумм.
Тогда наш многочлен будет выглядеть так: 
В примере 3 мы получили формулу: 
Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.
Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.
Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.
Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).
В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.
В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.
Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.
Нужна помощь с курсовой или дипломной работой?
Алгоритм определения симметричного многочлена. Решение симметричных уравнений
| Рубрика | Математика |
| Вид | курсовая работа |
| Язык | русский |
| Дата добавления | 12.02.2012 |
| Размер файла | 19,9 K |
Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже
Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.
Размещено на http://www.allbest.ru/
Цель работы: 1) разработка алгоритма определения симметричного многочлена. 2) разработка алгоритма решения симметричных уравнений, систем уравнений и задач, содержащих симметричные многочлены.
1. Примеры симметрических многочленов
Раскроем книгу В. Б. Лидского, Л. В. Овсянникова, А. Н. Тулайкова и М. И. Шабунина «Задачи по элементарной математике» (М., 1960). Среди наиболее трудных задач на решение систем уравнений высших степеней мы находим там (на стр. 11—12) следующие:
1) xІ + xy + yІ = 4 x + xy + y = 2
2) x + y = a + b xІ + yІ = aІ + bІ
3) xі + yі = 5aі xІy + xyІ = aі
5) 2(x + y) = 5xy 8(xі + yі) = 65
8) xІ + yІ = axy x + y = bxІyІ
Как известно из арифметики, сумма двух чисел не меняется при перестановке слагаемых, т. е. x + y = y + x для любых чисел x и y. Это равенство показывает, что многочлен x + y является симметрическим.
Точно так же из закона коммутативности умножения xy = yx следует, что произведение xy является симметрическим многочленом.
Симметрические многочлены x + y и xy являются самыми простыми. Их называют элементарными симметрическими многочленами от x и y. Для них используют специальные обозначения: a = x + y, a = xy.
2. Основная теорема о симметрических многочленах от двух переменных
Рассмотрение примеров делает это предположение вероятным. Например, степенные суммы.
Что и требовалось доказать.
3. Практическое применение
хІ + ху + уІ = 4 х + ху + у = 2
Уравнения этой системы являются симметричными, так как при замене х на у и у на х, уравнения не изменятся, тогда ввдем новые неизвестные а = х + у и а = ху.
Таким образом, система свелась к следующей:
Решая их, находим 4 пары ответов:
1) х = 2 2) х = 0 у = 0 у = 2
Рассмотрим еще один подобный пример:
Откуда получаем две системы решений:
симметрический многочлен уравнение теорема
1) х = 2 2) х = 3 у = 3 у = 2
1) в условии говорится о единственности решения
2) в уравнении или системе уравнений видна четность или нечетность функции, симметричность неизвестных. Покажем более подробно, как реализуется этот подход.
Найти все значения параметра а, при которых система уравнений имеет единственное решение
Вид данной системы убеждает нас в бесперспективности попыток анализа ее геометрического образа, также отсутствует квадратный трехчлен, дискриминант которого, можно было бы приравнять к нулю. Это является поводом поискать в задаче симметрию, тем более что в системе присутствую комбинации переменных вида x + y и ху. Вид второго уравнения, а именно, наличие в нем хІ и 2х, «подсказывает» выделить полный квадрат выражения
Алгебра и начала математического анализа. 10 класс
Конспект урока
Алгебра и начала математического анализа, 10 класс
Урок №13. Многочлены от нескольких переменных.
Перечень вопросов, рассматриваемых в теме
1) определение многочлена от нескольких переменных;
2) понятие симметрических многочленов;
3) формулы сокращенного умножения для старших степеней;
5) метод неопределенных коэффициентов.
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х.
Уравнение Р(x;y) = а, где 
Треугольник Паскаля —бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Многочлены от нескольких переменных можно складывать, вычитать, перемножать, возводить в натуральную степень, разлагать на множители — это вам известно из курса алгебры 7—9-го классов. Этот урок позволит нам несколько расширить знания о многочленах.
Воспользуемся методом группировки
(x+y+z+u) 2 =((x+y)+(z+u)) 2 = (x+y) 2 +2(x+y)(z+u)+(z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).
Итак, мы получили (x+y+z+u) 2 = x 2 +y 2 +z 2 +u 2 +2(xy+xz+xu+yz+yu+zu).
Среди многочленов от двух переменных выделяют однородные и симметрические многочлены.
Многочлен Р(х;у) называют однородным многочленом n-й степени, если сумма показателей степеней переменных в каждом члене многочлена равна n. Если Р(х;у) — однородный многочлен, то уравнение Р(х;у) = 0 называют однородным уравнением.
1) р(х; у)=2х+3у – однородный многочлен первой степени; соответственно 2х+3у=0 – однородное уравнение первой степени.
2) р(х; у)=3х 2 +5ху-7у 2 — однородный многочлен второй степени; соответственно 3х 2 +5ху-7у 2 =0 — однородное уравнение второй степени.
4) p(x; y)= anx n +an-1x n-1 y+an-2x n-2 y 2 +…+a1xy n-1 +a0y n — общий вид однородного многочлена n-й степени.
Рассмотрим еще один метод разложения многочленов на множители-
метод неопределенных коэффициентов. Суть метода неопределённых коэффициентов состоит в том, что вид сомножителей, на которые разлагается данный многочлен, угадывается, а коэффициенты этих сомножителей (также многочленов) определятся путём перемножения сомножителей и приравнивания коэффициентов при одинаковых степенях переменной. Теоретической основой метода являются следующие утверждения
Пример 3. Разложить на множители многочлен
3 x 3 – x 2 – 3 x + 1.
Решая эту систему, получаем: a = 3, p = –1, b = 2, c = –1. Итак, многочлен 3 x 3 – x 2 – 3 x + 1 разлагается на множители: 3 x 3 – x 2 – 3 x + 1 = ( x – 1)(3 x 2 + 2 x – 1).
Стоит отметить, что существует достаточно изящный способ решения однородных уравнений. Поясним его суть на примере.
Далее последовательно находим:
Если z=1, то 
Ответ: (t; t), где t- любое действительное число.
Теорема. Любой симметрический многочлен Р(х;у) можно представить в виде многочлена от ху и х+у.
x 4 +y 4 = 2xy(x 2 +y 2 )-(x 4 +y 4 )+3(xy) 2 и т.д.
Уравнение Р(x;y) = а, где 
А теперь перейдем к такому понятию как бином Ньютона.
Давайте вслед за Ньютоном попробуем ее вывести, чтобы затем применять.
Вы наверняка помните (или, по крайней мере, должны помнить), формулы сокращенного умножения для квадрата и куба суммы двух слагаемых (такая сумма называется «бином», по-русски – двучлен.
(a+b) 3 =a 3 +3a 2 b+3ab 2 +b 3
Если вы забыли эти формулы, можно их получить напрямую, раскрыв скобки в очевидных равенствах
Может быть, вам приходил в голову вопрос: можно ли (без компьютера) получить формулы типа для биномов четвертой степени, пятой, десятой – какой угодно?
Давайте попробуем дойти напрямую хотя бы до пятой степени, а там, может быть, окажется «рояль в кустах» (для порядка будем размещать слагаемые в правой части по убыванию степени а, она убывает от максимума до нуля):
(a+b) 4 =(a+b) 3 (a+b)=(a 3 +3a 2 b+3ab 2 +b 3 )(a+b)=a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4
(a+b) 5 =(a+b) 4 (a+b)=(a 4 +4a 3 b+6a 2 b 2 +4ab 3 +b 4 )(a+b)=a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +b 5
Теперь отдельно выпишем численные коэффициенты в правых частях формул при возведении бинома в заданную степень:
Легко проверить, что выписанные на численные коэффициенты – это строчки треугольника Паскаля, начиная с третьей. Этот «усеченный треугольник», в котором не хватает первых двух строк, легко сделать полным (получить строчки при n=0 и n=1):
Общая формула бинома Ньютона:

Правая часть формулы называется разложением степени бинома.

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.
Европейские ученые познакомились с формулой бинома Ньютона, по-видимому, через восточных математиков. Детальное изучение свойств биномиальных коэффициентов провел французский математик и философ Б. Паскаль в 1654 г.
В заключении рассмотрим пример, в котором использование бинома Ньютона позволяет доказать делимость выражения на заданное число.
Доказать, что значение выражения 5 n +28n-1, где n – натуральное число, делится на 16 без остатка.
Решение: представим первое слагаемое выражение как 5 n = (4+1) n и воспользуемся формулой бинома Ньютона:
Полученное произведение доказывает делимость исходного выражения на 16.
Бином Ньютона применяется при доказательстве Теоремы Ферма, в теории бесконечных рядов и выводе формулы Ньютона-Лейбница
Примеры и разборы решения заданий тренировочного модуля
Из данных многочленов выделите симметрические:
Решение: к данному заданию применим определение симметрических многочленов (Многочлен Р(х;у) называют симметрическим, если он сохраняет свой вид при одновременной замене х на у и у на х). Получим, что нам подходят 1 и 4 пункты.
(а+b) 5 = __a 5 +___a 4 b+___a 3 b 2 +___a 2 b 3 +___ab 4 +__b 5
Решение: для решения данного задания воспользуемся треугольником Паскаля
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Нас интересует последняя строчка.
Применив ее, получим ответ:
(а+b) 5 = 1a 5 +5a 4 b+10a 3 b 2 +10a 2 b 3 +5ab 4 +1b 5
Симметрические многочлены



Определение: Многочлен называется симметрическимесли он не меняется при любой перестановке переменных.
Пример: 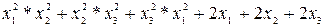
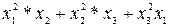
Строение симметрических многочленов можно представить в виде: Пусть 
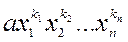
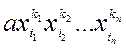
Симметрический многочлен является суммой однородных симметрических многочленов. Особую роль среди симметрических многочленов играют так называемые элементарные симметрические многочлены:
Определение: Многочлен называется однородным степени m,если все его члены имеют степень m.
Пример:
Очевидно, что сумма двух однородных многочленов одинаковой степени, есть однородный многочлен той же степени.
Произведение однородных многочленов степени 
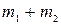
17. Многочлены над числовым полем.
Алгебраически замкнутое поле-это поле K в котором каждый многочлен не нулевой степени над полем K имеет хотя бы один корень.
Пример: поле комплексных чисел является алгебраически замкнутым.
Пример: поле действительных чисел не является алгебраически замкнутым, то есть:
Свойства:
1) В алгебраически замкнутом поле K каждый многочлен степени n имеет ровно n корней в этом поле ( с учетом кратности)
2) Конечные поля не могут быть алгебраически замкнутыми. Например: можно рассматривать многочлен конечной степени, корнями которого являются все элементы поля, если к нему прибавить единицу, то многочлен не будет иметь корней.
3) Алгебраическим замыканием поля действительных чисел является поле комплексных чисел, его алгебраическая замкнутость устанавливается основной теоремой алгебры.
4) Алгебраическим замыканием поля рациональных чисел является поле алгебраических чисел.
5) Поле арифметических чисел алгебраически замкнуто.
Определение: Число называется алгебраическим, если оно является корнем какого-либо алгебраического уравнения с целыми коэффициентами.
Пример:
Теорема Виета: Если многочлен P(x) степени n имеет n различных корней 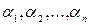
В случае, когда уравнение четвертой степени имеем: 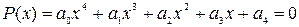
Корни будут:
Основная теорема алгебры (теорема Гаусса):Всякий многочлен n-ой степени имеет по крайней мере один комплексный корень.
Следствие: Многочлен степени n с комплексными коэффициентами и со старшим коэффициентом 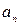
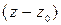
Теорема: Если многочлен с действительными коэффициентами имеет комплексный корень 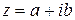
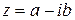
Теорема: Любой многочлен с действительными коэффициентами разлагается в произведение многочленов первой степени и второй степени (не имеющей действительных корней) с действительными коэффициентами.
Теорема: для того, чтобы несокращаемая дробь 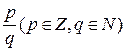
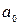
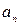

 .
. .
.
 первая формула такова:
первая формула такова:  .
.

 на множители.
на множители.