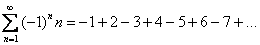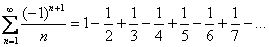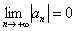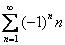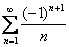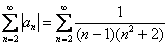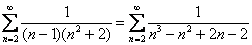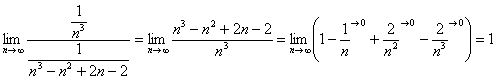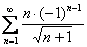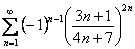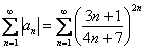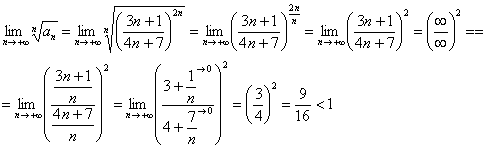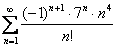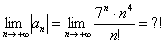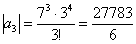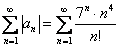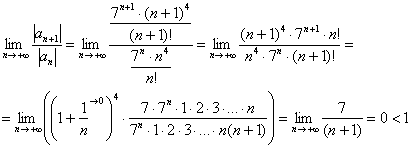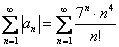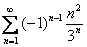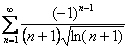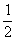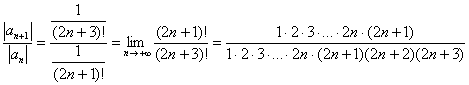Что значит сходится абсолютно
Абсолютно и условно сходящиеся ряды
Абсолютно сходящиеся ряды.
Ряд с действительными или комплексными членами
$$
\sum_
$$
называется абсолютно сходящимся, если сходится ряд
$$
\sum_
$$
Рассмотрим свойства абсолютно сходящихся рядов.
Если ряд абсолютно сходится, то он сходится.
\(\circ\) Пусть ряд \eqref
$$
\forall \varepsilon > 0\ \exists N_<\varepsilon>: \forall n \geq N_<\varepsilon>\ \forall p \in \mathbb
Если ряд \(\displaystyle\sum_
$$
\exists M > 0: \forall n \in \mathbb
$$
то ряд \(\displaystyle\sum_
\(\circ\) Для доказательства свойства 2 следует воспользоваться критерием Коши сходимости ряда и неравенством
$$
\sum_
$$
которое выполняется в силу условия \eqref
Если ряды \(\displaystyle\sum_
$$
\sum_
$$
\(\circ\) Для доказательства свойства 3 следует применить критерий Коши. \(\bullet\)
Если ряды \eqref
$$
\sum_
$$
абсолютно сходятся, то и ряд
$$
\sum_
$$
составленный из всевозможных попарных произведений членов рядов \eqref
\(\circ\) Докажем, что сходится ряд
$$
\sum_
$$
Пусть \(\tilde<\tau>_
$$
\tilde<\tau>_
$$
то есть частичные суммы ряда \eqref
Докажем, что
$$
\tau = S\sigma,\label
$$
где \(\tau\), \(S\), и \(\sigma\) — суммы рядов \eqref
Рис. 41.1
Занумеруем элементы этой таблицы, присваивая им номера, указанные в таблице (такой метод перечисления называют “методом квадратов”). В этом случае получается ряд
$$
a_<1>b_ <1>+ (a_<2>b_ <1>+ a_<2>b_ <2>+ a_<1>b_<2>) + (a_<3>b_ <1>+ a_<3>b_ <2>+ a_<3>b_ <3>+ a_<2>b_ <3>+ a_<1>b_<3>) +\\
+ (a_<4>b_ <1>+ a_<4>b_ <2>+ a_<4>b_ <3>+ a_<4>b_ <4>+ a_<3>b_ <4>+ a_<2>b_ <4>+ a_<1>b_<4>) + \ldots,\label
$$
образованный из всевозможных попарных произведений членов рядов \eqref
По доказанному выше всякий ряд вида \eqref
Пусть \(S_
Знакочередующиеся ряды. Признак Лейбница.
Абсолютная и условная сходимость
Для того чтобы понять примеры данного урока необходимо хорошо ориентироваться в положительных числовых рядах: понимать, что такое ряд, знать необходимый признак сходимости ряда, уметь применять признаки сравнения, признак Даламбера, признаки Коши. Тему можно поднять практически с нуля, последовательно изучив статьи Ряды для чайников и Признак Даламбера. Признаки Коши. Логически этот урок является третьим по счёту, и он позволит не только разобраться в знакочередующихся рядах, но и закрепить уже пройденный материал! Какой-то новизны будет немного, и освоить знакочередующиеся ряды не составит большого труда. Всё просто и доступно.
Что такое знакочередующийся ряд? Это понятно или почти понятно уже из самого названия. Сразу простейший пример.
Рассмотрим ряд 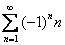
А сейчас будет убийственный комментарий. У членов знакочередующегося ряда чередуются знаки: плюс, минус, плюс, минус, плюс, минус и т.д. до бесконечности.
Знакочередование обеспечивает множитель 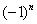
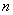
В практических примерах знакочередование членов ряда может обеспечивать не только множитель 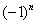
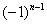
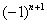
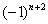
Подводным камнем являются «обманки»: 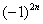
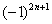
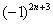
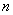
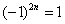
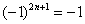
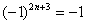
Как исследовать знакочередующийся ряд на сходимость? Использовать признак Лейбница. Про немецкого гиганта мысли Готфрида Вильгельма Лейбница я рассказывать ничего не хочу, так как помимо математических трудов, он накатал несколько томов по философии. Опасно для мозга.
Признак Лейбница: Если члены знакочередующегося ряда монотонно убывают по модулю, то ряд сходится.
1) Ряд является знакочередующимся.
2) Члены ряда убывают по модулю: 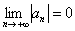
Если выполнены эти условия, то ряд сходится.
Краткая справка о модуле приведена в методичке Горячие формулы школьного курса математики, но для удобства ещё раз:
Что значит «по модулю»? Модуль, как мы помним со школы, «съедает» знак «минус». Вернемся к ряду 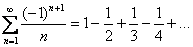
– Члены ряда без учёта знака убывают.
– Члены ряда убывают по модулю.
– Члены ряда убывают по абсолютной величине.
– Модуль общего члена ряда стремится к нулю:
// Конец справки
Теперь немного поговорим про монотонность. Монотонность – это скучное постоянство.
Члены ряда строго монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю МЕНЬШЕ, чем предыдущий: 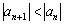
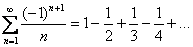
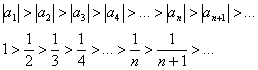
А можно сказать короче: каждый следующий член ряда по модулю меньше, чем предыдущий: 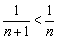
Члены ряда нестрого монотонно убывают по модулю, если КАЖДЫЙ СЛЕДУЮЩИЙ член ряда по модулю НЕ БОЛЬШЕ предыдущего: 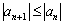
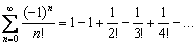
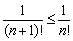
В условиях теоремы Лейбница должна выполняться монотонность убывания (неважно, строгая или нестрогая). Кроме того, члены ряда могут даже некоторое время возрастать по модулю, но «хвост» ряда обязательно должен быть монотонно убывающим.
Не нужно пугаться того, что я нагородил, практические примеры всё расставят по своим местам:
Исследовать ряд на сходимость
В общий член ряда входит множитель 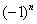
1) Проверка ряда на знакочередование. Обычно в этом пункте решения ряд расписывают подробно 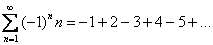
2) Убывают ли члены ряда по модулю? Здесь нужно решить предел 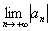
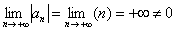
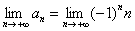
* Согласно, строгому определению предела числовой последовательности, и кроме того, в данном случае это очевидно.
Вывод: ряд расходится.
Как разобраться, чему равно 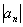
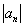
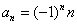
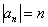
Исследовать ряд на сходимость
Используем признак Лейбница:
1) 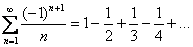
Ряд является знакочередующимся.
2) 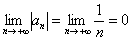
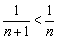
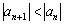
Вывод: ряд сходится.
Однако это еще не всё! Сходимость бывает разной. А именно:
– сходящийся ряд 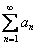
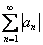
в противном случае ряд 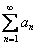
! Из вышесказанного очевидно следует, что любой сходящийся положительный ряд является абсолютно сходящимся.
Составим ряд из модулей – опять просто убираем множитель, который обеспечивает знакочередование:
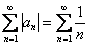
Таким образом, наш ряд 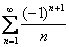
Следует отметить, что при формулировке «Исследуйте ряд на сходимость» можно рискнуть и ограничиться признаком Лейбница (т.е. просто констатировать сходимость), но таки лучше не лениться – с большой вероятностью вас попросят уточнить, сходится ли ряд абсолютно или условно.
Заметьте также, что в Примере 1 второй этап по-любому отпадает, поскольку еще на первом шаге сделан вывод о том, что ряд расходится.
Собираем ведёрки, лопатки, машинки и выходим из песочницы, чтобы смотреть на мир широко открытыми глазами из кабины моего экскаватора:
Исследовать ряд на сходимость
Используем признак Лейбница:
1) 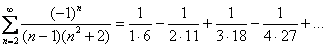
Данный ряд является знакочередующимся.
2) 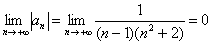
Для любого номера 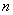
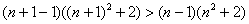
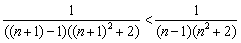
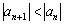
Вывод: ряд сходится.
Теперь выясним, как именно. Для этого составим и исследуем соответствующий ряд из модулей:
Анализируя начинку, приходим к выводу, что здесь нужно использовать предельный признак сравнения. Скобки в знаменателе удобнее раскрыть:
Сравним данный ряд со сходящимся рядом 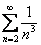
Получено конечное число, отличное от нуля, значит, ряд 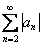
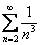
Таким образом, ряд 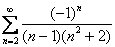
Исследовать ряд на сходимость
Исследовать ряд на сходимость
Это примеры для самостоятельного решения. Полное решение и образец оформления в конце урока.
Как видите, знакочередующиеся ряды – это просто и занудно! Но не спешите закрывать страницу, всего через пару экранов мы рассмотрим случай, который многих ставит в тупик. А пока еще пара примеров для тренировки и повторения.
Исследовать ряд на сходимость
Используем признак Лейбница:
1) Ряд является знакочередующимся.
2) 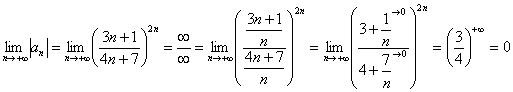
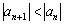
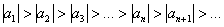
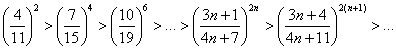
Вывод: ряд сходится.
Обратите внимание, что я не расписал подробно члены ряда. Их всегда желательно расписывать, но от непреодолимой лени в «тяжелых» случаях можно ограничиться фразой «Ряд является знакочередующимся». Кстати, не нужно относиться к этому пункту формально, всегда проверяем (хотя бы мысленно) что ряд действительно знакочередуется. Помните об «обманках» 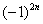
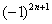
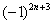
Выясним характер сходимости ряда:
Очевидно, что нужно использовать радикальный признак Коши:
Таким образом, ряд 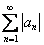
Исследуемый ряд сходится абсолютно.
Исследовать ряд на сходимость
Это пример для самостоятельного решения. Хммм… что-то я немного погорячился на счет простоты.
Нередко встречаются знакочередующиеся ряды, которые вызывают затруднения.
Исследовать ряд на сходимость
Используем признак Лейбница:
1) Ряд является знакочередующимся.
2)
Дело в том, что не существует стандартных обыденных приемов для решения подобных пределов. Куда стремится такой предел? К нулю, к бесконечности? Здесь важно знать, ЧТО на бесконечности растёт быстрее – числитель или знаменатель.
Примечание: понятие порядка роста функции подробно освещено в статье Методы решения пределов. У нас пределы последовательностей, но это не меняет сути.
Если числитель 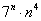
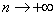
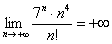
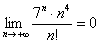
Попробуем записать несколько первых членов ряда: 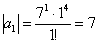
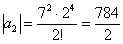
Создается стойкое впечатление, что 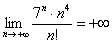
Обратимся к теории математического анализа, для того она и существует:
Справка:
– Факториал растёт быстрее, чем показательная последовательность 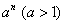
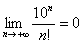
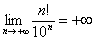
– Факториал растёт быстрее, чем степеннАя последовательность 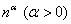
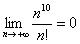
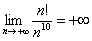
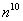
– Факториал растёт быстрее произведения показательной 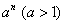
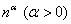
И, раз пошла такая пьянка:
– Показательная последовательность 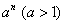
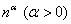
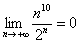
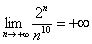
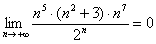
– А есть ли что-нибудь «круче» факториала? Есть! Степенно-показательная последовательность 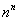
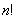
Таким образом, второй пункт исследования (вы еще о нём помните? =)) можно записать так:
2) 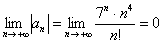
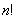
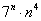
Достаточно! О том, что члены начинают убывать лишь с некоторого номера «эн», лучше благоразумно умолчать – по той причине, что найти этот номер не так-то просто, а лишние вопросы вам ни к чему 😉 Ещё труднее показать монотонность убывания, поэтому просто констатируем этот факт. Здесь вас с высокой вероятностью «простят»
Вывод: ряд сходится.
Исследуем ряд, составленный из модулей членов:
А тут уже работает старый добрый признак Даламбера:
Таким образом, ряд 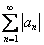
Исследуемый ряд сходится абсолютно.
Разобранный пример можно решить другим способом.
Теорема: если ряд 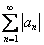
Пример 8 «на бис» вторым способом.
Исследовать ряд на сходимость
Решение: исследуем сходимость ряда, составленного из модулей:
Используем признак Даламбера:
…
только что печатал
…
Таким образом, ряд 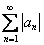
Вывод: ряд 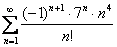
Правда, при втором способе решения есть риск, что преподаватель оценит хитро… смекалку студента и забракует задание. А может и не забракует. Ибо условие не предписывает использовать именно признак Лейбница (но обычно это всё же подразумевается).
И напоследок пара примеров для самостоятельного решения. Один из той же оперы (перечитайте справку), но попроще. Другой для гурманов – на закрепление интегрального признака сходимости.
Исследовать ряд на сходимость
Исследовать ряд на сходимость
После качественной проработки числовых положительных и знакопеременных рядов с чистой совестью можно перейти к функциональным рядам, которые не менее монотонны и однообразны интересны.
Пример 4: Используем признак Лейбница:
1) 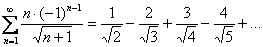
2)
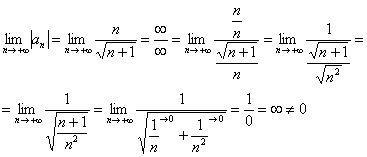
Члены ряда не убывают по модулю, следовательно, предела 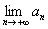
Вывод: ряд расходится.
Примечание: в данном примере неопределенность 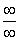
Пример 5: Используем признак Лейбница.
1) 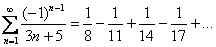
2) 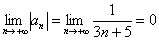
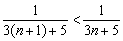
Таким образом, ряд сходится по признаку Лейбница.
С помощью ряда, составленного из модулей, выясним как именно: 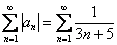
Сравним данный ряд с расходящимся гармоническим рядом 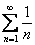
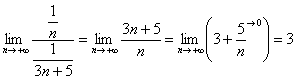
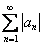
Таким образом, ряд 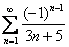
Пример 7: Используем признак Лейбница.
1) 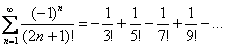
2) 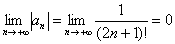
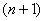
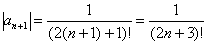
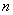
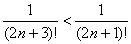
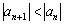
Ряд сходится по признаку Лейбница.
Исследуем характер сходимости: 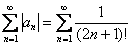
Используем признак Даламбера: 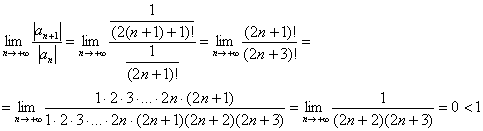
Таким образом, ряд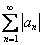
Ряд 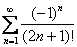
Примечание: Возможно, не всем понятно, как разложены факториалы. Это всегда можно установить опытным путём, возьмём и сравним какие-нибудь соседние члены ряда:
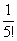
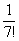
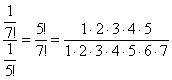
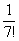
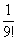
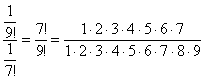
…
Таким образом, ряд сходится. Выясним, абсолютно или условно: 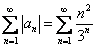
Используем признак Даламбера: 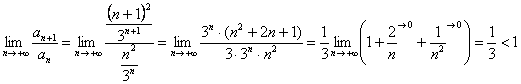
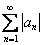
Исследуемый ряд сходится абсолютно.
Пример 10: Используем признак Лейбница.
1) 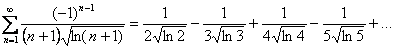
Ряд является знакочередующимся.
2) 
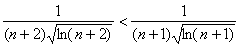
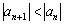
Ряд сходится по признаку Лейбница.
Исследуем ряд, составленный из модулей: 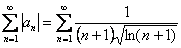
Используем интегральный признак.
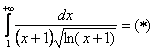
Подынтегральная функция непрерывна на 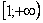
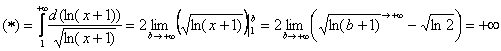
Таким образом, ряд 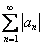
Исследуемый ряд сходится условно.
Автор: Емелин Александр
(Переход на главную страницу)