Что значит сформулировать признак делимости

Признаки делимости чисел

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Что такое «признак делимости»

Признак делимости числа — это такая особенность числа, которая еще до выполнения деления позволяет определить, кратно ли число делителю.

Истинный путь джедая, чтобы зря не пыхтеть над числами, которые в конечном итоге не делятся.

Однозначные, двузначные и трехзначные числа

Однозначное число — это такое число, в составе которого один знак (одна цифра). Девять однозначных натуральных чисел: 1, 2, 3, 4, 5, 6, 7, 8, 9.

Двузначные числа — такие, в составе которых два знака (две цифры). Цифры могут повторяться или быть различными.

Трехзначные числа — числа, в составе которых три знака (три цифры).

Чётные и нечётные числа

Число называют четным тогда, когда оно делится на два без остатка. А нечетные числа — те, что на два без остатка не делятся. Все просто!

Признаки делимости чисел

Признак делимости на 2. Сразу можно сказать, что число делится на 2, если последняя цифра четная.

Признак делимости на 3. Сумма цифр числа должна делиться на 3.

Признаки делимости на 4. Число делится на 4, если две последние цифры — 0 или если они образуют цифру, которая делится на 4.

Признаки делимости на 5. Число делится на 5, если заканчивается на 0 или 5.

Признак делимости на 6. На 6 делятся те числа, которые могут одновременно делится на 2 и на 3.

Признаки делимости на 8. Число делится на 8, если три последних цифры — 0 или если они образуют число, которое делится на 8.

Признак делимости на 9. Число делится на 9, если сумма цифр делится на 9.

Признаки делимости на 10, 100. Числа, которые заканчиваются на 0, 00, 000 делятся на 10, 100, 1000 и так далее.

Курсы обучения математике помогут подтянуть оценки, подготовиться к контрольным, ВПР и экзаменам.

Источник

Делимость чисел. Признаки делимости. Основная теорема арифметики

В этой статье – необходимая теория для решения задачи 18 Профильного ЕГЭ по математике. Но это не все. Знания о числах и их свойствах, признаки делимости и формула деления с остатком могут пригодиться вам при решении многих задач ЕГЭ.
Повторим еще раз, какие бывают числа.

Например, при делении 9 на 4 мы получаем частное 2 и остаток 1, то есть 9 = 4∙2 + 1.

Простые числа – те, что делятся только на себя и на единицу. Единица не является ни простым, ни составным числом. Простые числа: 2, 3, 5, 7, 11, 13, 17, 19…

Числа называются взаимно простыми, если они не имеют общих делителей, кроме 1.

Любое натуральное число можно разложить на простые множители.

Например, 72 = 2∙2∙2∙3∙3, а 98 = 2∙7∙7.

Основная теорема арифметики: Любое натуральное число можно представить в виде произведения простых делителей, взятых в натуральных степенях, причем это разложение единственно.

Наименьшее общее кратное двух чисел (НОК) — это наименьшее число, которое делится на оба данных числа.

Наибольший общий делитель двух чисел (НОД) — это наибольшее число, на которое делятся два данных числа.

последняя цифра числа четная;

сумма цифр числа делится на 3;

число заканчивается на 0 или на 5;

сумма цифр числа делится на 9;

последняя цифра числа равна 0;

суммы цифр на четных и нечетных позициях числа равны или их разность кратна 11.

Источник

Какие признаки делимости чисел существуют

Признаки делимости чисел в математике — объяснение

Признаки делимости чисел — это условия, правила, по которым можно определить, делится ли число на заданное нам значение, т.е. кратно ли число делителю.

Делителем является число, на которое делится заданное число без остатка — нацело.

Термин «кратно» — синоним слову «делится».

Правила с доказательствами, определение

Любое натуральное число, которое оканчивается цифрой 0, делится без остатка на 10. Чтобы получить частное, нужно отбросить нуль.

Если запись натурального числа заканчивается нулем, то число делится на 10 нацело.

Если запись натурального числа заканчивается любой другой цифрой, то число не делится нацело на 10.

Но 378 не делится без остатка на 10, потому что получим неполное частное: 378 : 10 = 37 (остаток 8 ).

На конце числа 378 стоит цифра 8 — она и будет остатком при делении на 10. Значит, 378 не делится нацело на 10.

Применение признака позволяет не производить расчеты, а сразу отвечать на вопрос, делится ли заданное число на десять.

Тогда число 5 является делителем числа 20, т. е. 20 делится на пять нацело, без остатка.

Тогда число 5 является делителем числа 15, т. е. 15 делится на 5 нацело.

В разрядах единиц 20 и 15 стоят 0 и 5 соответственно.

Разряд — это место цифры в числе.

Если запись натурального числа заканчивается цифрами 0 или 5, то такое число делится нацело на 5.

Можно перефразировать признак:

Если в разряде единиц заданного числа стоит 0 или 5, то число делится на 5.

Если запись натурального числа заканчивается цифрой, отличной от нуля и пяти, то число на 5 нацело не делится.

Числа 645 и 760 делятся на 5, так как они заканчиваются 5 и 0 соответственно.

344 не делится нацело на 5 по признаку делимости:

Если число делится нацело на 2, то его называют четным. Если число не делится нацело на 2, то его называют нечетным.

Цифры 0, 2, 4, 6, 8 — четные, а 1, 3, 5, 7, 9 — нечетные. Тогда любое число будет четным, если в разряде единиц у него стоит четная цифра, а нечетным — в разряде единиц стоит нечетная цифра.

Если запись натурального числа оканчивается четной цифрой, то число делится на 2 нацело.

Если натуральное число оканчивается нечетной цифрой, то не делится нацело на 2.

Числа 14 и 56 делятся нацело на 2, так как они заканчиваются четными цифрами — 4 и 6.

Число 13 не делится нацело на 2, так как запись натурального числа заканчивается нечетной цифрой 3.

Если сумма цифр числа делится нацело на 9, то и само число делится нацело на 9.

Если сумма цифр числа не делится нацело на 9, то и само число не делится нацело на 9.

Рассмотрим, делится ли 98 на 9.

Сумма цифр числа: 9+8=17.

17 не делится нацело на 9, тогда число 98 не делится нацело на 9.

Проверяем: 98 : 9 = 10 (остаток 8 ).

18 делится нацело на 9, значит, 468 делится нацело на 9:

Если сумма цифр числа делится нацело на 3, то и само число делится нацело на 3.

Если сумма цифр числа не делится нацело на 3, то и само число не делится нацело на три.

Число 27 делится нацело на 3, так как сумма цифр делится на 3 нацело.

И, соответственно, 27:3=9.

Число 261 делится на 3 по признаку делимости:

Девять делится на 3 нацело, значит, число 261 делится на 3 нацело.

Дополнительные признаки делимости:

Натуральное число делится на 4 нацело в том случае, когда запись числа заканчивается двумя нулями или две последние цифры делятся на 4.

Например, по этому признаку число 144 делится на 4, так как 44 — две последние цифры — делится нацело на 4.

Натуральное число делится на 6 нацело тогда, когда число делится нацело и на 2, и на 3.

Значит, признак делимости на 6 включает в себя применения признака делимости на два и признака делимости на три.

Например, число 438 делится на 6 нацело.

Используя признак делимости на 6, поочередно применяем признаки делимости на 2 и 3.

Если число заканчивается четной цифрой, то оно делится на 2: число 438 заканчивается четной цифрой 8.

Значит, число делится и на 2, и на 3. Тогда 438 делится на 6 нацело.

Натуральное число делится на 8 нацело, если запись числа заканчивается тремя нулями либо если три последние цифры образуют число, которое делится на 8.

Например, 58000 делится на 8 по признаку делимости, так как число заканчивается тремя нулями.

Остальные признаки делимости можно вывести самостоятельно.

Где применяется в жизни

В жизни признаки делимости удобно применять тогда, когда под рукой нет гаджетов. И процесс определения делимости чисел значительно упрощается. При этом не нужно даже высчитывать результат непосредственного деления, если в задаче необходимо просто определить, делится ли одно число на другое.

Области применения признаков делимости:

Примеры решения задач

Назовите 3 числа, которые делятся на 2.

Вспоминаем признак делимости на 2:

Если число заканчивается четной цифрой, то оно делится на 2.

Тогда искомыми числами могут быть, например: 456, 768, 800.

Цифры 6, 8, 0 — четные: значит, числа 456, 768, 800 делятся на 2.

Какие из чисел 234, 450, 400, 3400, 35, 900, 235 000 делятся на 100?

Мы знаем признак делимости на 10:

Если число заканчивается 0, то число делится на 10.

Когда нужно определить, делится ли число на 100, действуем аналогично признаку делимости на 10. Только в этом случае нужно искать те числа, которые заканчиваются двумя нулями.

Тогда в ответе будут числа: 400, 3400, 900, 235 000.

Аналогично действуем тогда, когда нужно найти числа, которые делятся на 1000, 1000 и так далее. Ищем числа по количеству нулей после единицы в делителе.

Какие из чисел 100, 35, 450, 5680, 20 делятся и на 5, и на 10.

Число делится на 5, если заканчивается 0 или 5.

Число делится на 10, если заканчивается 0.

Тогда, чтобы число делилось и на 5, и на 10, нужно найти в признаках что-то общее. Общим будет окончание чисел на 0.

По признакам делимости на 5, и на 10 получаем в ответе числа: 100, 450, 5680 и 20.

Найдите три числа, которые делятся на 2 и на 9.

Чтобы число делилось и на 2, и на 9, должны выполняться условия обоих признаков.

Число делится на 2 тогда, когда оканчивается четной цифрой. Четные цифры — это 0, 2, 4, 6, 8.

Число делится на 9 тогда, когда сумма цифр числа делится на 9.

Тогда искомыми числами могут быть: 18, 396 и 468.

В разряде единиц в 18, 396 и 468 стоят 8, 6 и 8 соответственно — четные цифры, значит числа 18, 396 и 468 делятся на 2.

Осталось проверить, делятся ли они на 9. Считаем сумму цифр в числах.

Значит, числа 18, 396 и 468 делятся на 9.

Числа удовлетворяют условиям.

Ответ: 18, 396 и 468.

Какие из чисел 456, 567, 3453, 768 и 34500 кратны 3?

Слово «кратно» является синонимом «делится». Тогда нужно найти числа, которые делятся на 3.

По признаку делимости искомыми будут числа, сумма цифр которых делится на три нацело.

Выбираем те числа, сумма которых делится на 3:

456, так как сумма цифр равна 15, а 15 делится на 3 нацело;

567, потому что сумма цифр равна 18, а 18 делится на 3 нацело;

3453 — сумма цифр равна 18, значит, число делится на 3;

768 — сумма цифр равна 21, значит, число делится на 3.

Источник

Делимость чисел. Признак делимости

Определение 1. Пусть число a 1 ) есть произведение двух чисел b и q так, что a=bq. Тогда a называется кратным b.

1 ) В данной статье под словом число будем понимать целое число.

Можно сказать также a делится на b, или b есть делитель a, или b делит a, или b входит множителем в a.

Из определения 1 вытекают следующие утверждения:

Действительно. Так как

где m и n какие то числа, то

Следовательно a делится на c.

Если в ряду чисел, каждое делится на следующее за ним, то каждое число есть кратное всех последующих чисел.

Действительно. Так как

Признаки делимости

Выведем общую формулу для определения признака делимости чисел на некоторое натуральное число m, которое называется признаком делимости Паскаля.

Найдем остатки деления на m следующей последовательностью. Пусть остаток от деления 10 на m будет r₁, 10&middotr₁ на m будет r₂, и т.д. Тогда можно записать:

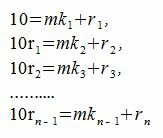(1)

Так как при делении любого числа на m остатки могут быть 0,1. m-1, то через m шагов остатки от деления на m будут повторяться (следовательно пересчитать их не нужно).

Любое натуральное число A в десятичной системе счисления можно представить в виде

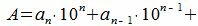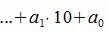(2)

Докажем, что остаток деления числа A на m равна остатку деления числа

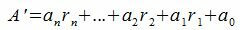(3)

Как известно, если два числа при делении на какое то число m дают одинаковый остаток, то из разность делится на m без остатка.

Рассмотрим разность A−A’

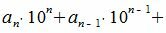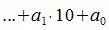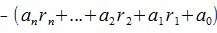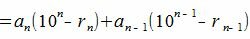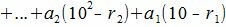(4)

Покажем, что 10 i −r_i делиться на m при всех i=1,2. m−1.

10−r_i=mk₁ делится на m (т.к. mk₁ кратно m),

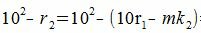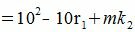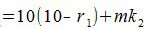(5)

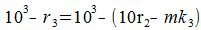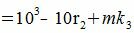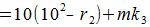(6)

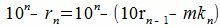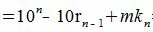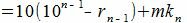(7)

Исходя из выражения (3), можно получить признаки делимости для конкретных чисел.

Признаки делимости чисел 2, 3, 4, 5, 6, 7, 8, 9, 10

Признак делимости на 2.

Следуя процедуре (1) для m=2, получим:

Все остатки от деления на 2 равняются нулю. Тогда, из уравнения (3) имеем

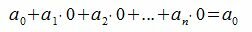Следовательно число делится на 2 тогда и только тогда, когда его последняя цифра делиться на 2 (т.е. когда число является четным).

Признак делимости на 3.

Следуя процедуре (1) для m=3, получим:

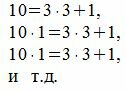Все остатки от деления на 3 равняются 1. Тогда, из уравнения (3) имеем

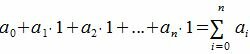Следовательно число делится на 3 тогда и только тогда, когда сумма всех его цифр делится на 3.

Признак делимости на 4.

Следуя процедуре (1) для m=4, получим:

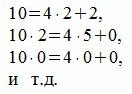Все остатки от деления на 4 кроме первого равняются 0. Тогда, из уравнения (3) имеем

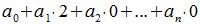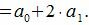Следовательно число делится на 4 тогда и только тогда, когда удвоенное число десятков сложенное с числом единиц делится на 4. Число делится на 4, если последние две цифры составляют число, делящееся на 4.

Признак делимости на 5.

Следуя процедуре (1) для m=5, получим:

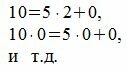Все остатки равны нулю. Тогда, из уравнения (3) имеем

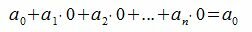Следовательно число делится на 5 тогда и только тогда, когда последняя цифра этого числа делится на 5, т.е. число оканчивается на 0 или 5.

Признак делимости на 6.

Следуя процедуре (1) для m=6, получим:

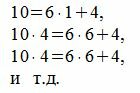Все остатки равны 4. Тогда, из уравнения (3) имеем

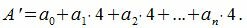Следовательно число делится на 6 тогда и только тогда, когда учетверённое число десятков, сложенное с числом единиц, делится на 6. То есть из числа отбрасываем правую цифру, далее суммируем полученное число с 4 и добавляем отброшенное число. Если данное число делится на 6, то исходное число делится на 6.

Пример. 2742 делится на 6, т.к. 274*4+2=1098, 1098=109*4+8=444, 444=44*4+4=180 делится на 6.

Более простой признак делимости. Число делится на 6, если оно делится на 2 и на 3 (т.е. если оно четное число и если сумма цифр делится на 3). Число 2742 делится на 6, т.к. число четное и 2+7+4+2=15 делится на 3.

Признак делимости на 7.

Следуя процедуре (1) для m=7, получим:

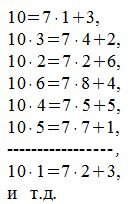Все остатки разные и повторяются через 7 шагов. Тогда, из уравнения (3) имеем

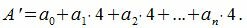(8)

Следовательно число делится на 7 тогда и только тогда, когда (8) делится на 7.

Пример. 3801 делится на 7, т.к. 1+0*3+8*2+3*6=1+16+18=35 делится на 7.

Другой признак делимости. Для определения, делится ли число на 7, из числа отбрасываем последнюю с права цифру, далее умножаем полученное число на 3 и добавляем и добавляет отброшенное число. Если данное число делится на 7, то исходное число делится на 6. 380*3+1=1141, 114*3+1=343, 34*3+3=105, 10*3+5=35 делится на 7, следовательно 3801 делится на 7.

Признак делимости на 8.

Следуя процедуре (1) для m=8, получим:

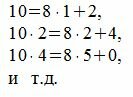Все остатки все остатки нулевые, кроме первых двух. Тогда, из уравнения (3) имеем

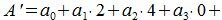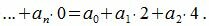(9)

Следовательно число делится на 8 тогда и только тогда, когда (9) делится на 8.

Пример. 4328 делится на 8, т.к. 8+2*2+4*3=24 делится на 8.

Признак делимости на 9.

Следуя процедуре (1) для m=9, получим:

Все остатки от деления на 9 равняются 1. Тогда, из уравнения (3) имеем

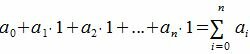Следовательно число делится на 9 тогда и только тогда, когда сумма всех его цифр делится на 9.

Признак делимости на 10.

Следуя процедуре (1) для m=10, получим:

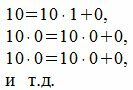Все остатки от деления на 10 равняются 0. Тогда, из уравнения (3) имеем

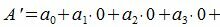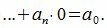Следовательно число делится на 10 тогда и только тогда, когда последняя цифра делится на 10 (то есть последняя цифра нулевая).

Источник

Признаки делимости

Всего получено оценок: 205.

Всего получено оценок: 205.

Признаки делимости чисел сложно применять, поскольку их достаточно много. Зато знание таких признаков существенно экономит время, поскольку позволяет без деления узнать, делиться одно число на другое или нет. Разберемся в теме подробнее.

Что такое делимость?

Признаки делимости позволяют просто и быстро определить, возможно ли полностью поделить одно число на другое. А делимость это и есть возможность поделить одно число на друге без остатка.

Признаки делимости

Признаки делимости удобнее изучать, разбив возможные делители на группы. Поступим так же и рассмотрим делимость на каждую из групп в отдельности.

На 2,4,8

Эти числа в рассматриваемом вопросе сгруппированы, так как их признаки очень похожи друг на друга.

На 3 и 9

Число делится на 3, если сумма цифр этого числа делится на 3. Рассмотрим число: 804. Оно делится на 3, поскольку сумма цифр 8+0+4=12 – делится на 3.

Число делится на 9, если сумма цифр числа делится на 9. Признак похож на признак делимости на число 3.
Интересно: Если число делится на 9, то оно делится и на 3. При этом, число, которое делится на 3 не всегда делится на 9.

Число делится на 5, если последняя цифра числа равняется 5 или нулю. Это наиболее известный признак делимости, наряду с делимостью на 2.

Чтобы число делилось на 6, оно должно делиться на 2 и 3, так как 2*3=6. Поэтому признак делимости на 6 это объединение признаков деления на 2 и на 3.

То есть: число делится на 6, если оно четное и сумма всех его цифр делится на 3

Самые сложные в восприятии признаки делимости на 7 и на 11. Число делится на 7, если разность сумм четных цифр числа и нечетных цифр чисел делится на 7.

Приведем пример: число 469 делится на 7. Почему? Сумма цифр на нечетных позициях 4+9=13. Сумма чисел на четных позициях 6. Разность получившихся сумм: 13-6=7, а это число делится на 7. Поэтому все число 469 делится на 7

На 10

Число делится на 10 только если последней цифрой числа является 0

По тому же принципу определяют делимость числа на 100, 1000 и так далее. Если у числа два нуля на конце, то оно делится на 100, если три нуля на конце, число делится на 1000 и так далее.

На 11

Число делится на 11 только, если разность сумм четных и нечетных цифр числа делится на 11 или равняется нулю Приведем пример:

Число 2035 делится на 11. Сумма цифр, стоящих на четных позициях: 2+3=5. Сумма нечетных цифр: 0+5=5. Разность полученных выражений:5-5=0, значит число делится на 11.

Нельзя путать понятия четной позиции и четного числа. Цифра это знак, который используется для записи чисел. Число это набор цифр, каждая из которых стоит на своей позиции. В числе 127 всего три цифры. Цифра 1 стоит на первой позиции, цифра 2 на второй и так далее. На четной позиции находится цифра 2. На нечетных позициях цифры 1 и 7.

Чтобы быстрее запомнить все группы можно свести в таблицу признаков делимости чисел.

Признаки

Запомни

Признак делимости на 2

Число делится на 2, если его последняя цифра делится на 2 или является нулём.

Признак делимости на 4

Число делится на 4, если две его последние цифры нули или образуют число, делящееся на 4.

Признак делимости на 8

Число делится на 8, если три последние его цифры нули или образуют число, делящееся на 8.

Признак делимости на 3

Число делится на 3, если сумма всех его цифр делится на 3.

Признак делимости на 6

Число делится на 6, если оно делится одновременно на 2 и на 3.

Признак делимости на 9

Число делится на 9, если сумма всех его цифр делится на 9.

Признак делимости на 5

Число делится на 5, если его последняя цифра 5 или 0.

Признак делимости на 25

Число делится на 25, если его две последние цифры нули или образуют число, которое делится на 25.

Признак делимости на 10,100 и 1000.

10 делятся нацело только те числа, последняя цифра которых нуль.

На 100 делятся нацело только те числа, две последние цифры которых нули.

На 1000 делятся нацело только те числа, три последние цифры нули.

Признак делимости на 11

Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.

Что мы узнали?

Мы поговорили о признаках делимости. Расписали все существующие признаки по группам. В особо сложных ситуациях привели примеры.

Источник