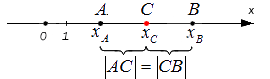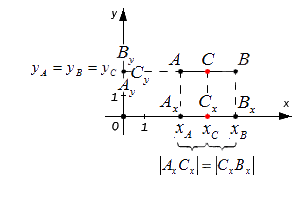Что значит середина отрезка
Отрезок
Определение отрезка
Определение 1. Отрезок (или отрезок прямой )− это часть прямой, ограниченная двумя точками.
Определение 2. Отрезок − это множество, состоящая из двух различных точек данной прямой и всех точек, лежащих между ними.
Точки, ограничивающие отрезки называются концами отрезка, а точки, которые находятся между концами отрезка называются внутренними точками.
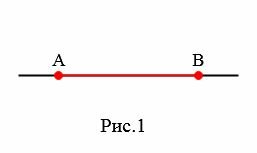 |
На рисунке 1 отрезок выделен красным цветом. Точки A и B концы отрезка, а точки между ними − внутренние точки.
Обозначение отрезков
Отрезки обозначаются с помощью его конечных точек. Отрезок на рисунке 1 обозначается так: AB или BA. Порядок следования имен конечных букв не имеет значения.
Сравнение отрезков
Для сравнения отрезков нужно:
Если два других конца совместяться, то отрезки равны. Если же конец одного отрезка находится внутри другого, то длина первого отрезка меньше второго.
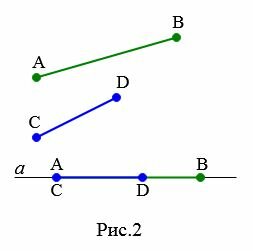 |
Пусть даны два отрезка AB и CD (Рис.2). Требуется сравнить эти отрезки, т.е. определить какой из них больше. Отложим эти отрезки на прямой a. Как видим, точка D находится внутри отрезка AB. Значит отрезок CD меньше отрезка AB. Это обозначается так: CD Определение 3. Точка отрезка,делящая его на два равных отрезка называется серединой отрезка.
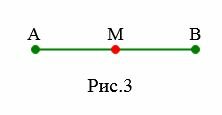 |
На рисунке 3 \( \small M \) является серединой отрезка \( \small AB \) поскольку \( \small AM = MB \).
Длина отрезка
Для определения длины отрезка его нужно сравнить с другим отрезком, принятым за единицу измерения.
В качестве единицы измерения можно взять, например, сантиметр. В этом случае для определения длины отрезка узнают, сколько раз в данном отрезке укладывается сантиметр. Этот показатель и является длиной отрезка выраженная в сантиметрах. Если длина отрезка AB равна трем сантиметрам, то пишут AB=3см.
Если отрезок, принятый за единицу измерения не укладывается целое число раз в измеряемом отрезке, то его обычно делят на 10 равных частей и определяют сколько раз одна такая часть укладывается в остатке. Одна десятая часть сантиметра называется миллиметром. В итоге получаем длину отрезка в сантиметрах и миллиметрах.
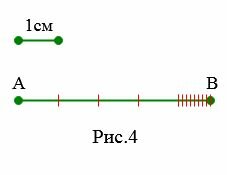 |
На Рис.4 1см укладывается в отрезке AB 4 раза и в остатке укладывается ровно 8 одну десятую часть сантиметра. Поэтому можно писать: AB=4см 8мм или AB=4.8см.
Направленный отрезок
Если для отрезка определить направление, то такой отрезок называется направленным отрезком. Направленный отрезок имеет начальную точку и конечную точку. В конечной точке направленного отрезка рисуют стрелку (Рис.5)
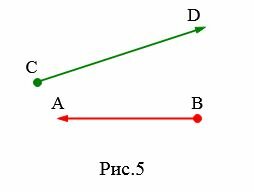 |
Для обозначения направленных отрезков сначала пишется начальная точка, а затем конечная точка. На рисунке 2 верхний направленный отрезок обозначают так: \( \small \overrightarrow
Что такое середина отрезка
Ответ или решение 2
Определение координат середины отрезка
Определение середины отрезка графически
Для определение середины отрезка графически нужны:
Действия проводится в следующем порядке:
1) один конец циркуля с иглой устанавливается в любой конец отрезка;
2) раскрываем циркуль на расстояние визуально большее, чем половина отрезка и меньшее, чем весь отрезок;
3) проводим вторым концом циркуля с грифелем над отрезком дугу и под отрезком такую же дугу;
4) переносим иглу циркуля в другой конец отрезка;
5) вторым концом циркуля с грифелем над отрезком проводим дугу до пересечения с первой дугой над отрезком;
6) аналогично находим точку пересечения двух дуг под отрезком;
7) проводим через две полученные точки прямую;
8) точка пересечения исходного отрезка и проведенной прямой является серединой заданного отрезка.
Середина отрезка — это такая точка, которая делит отрезок (множество, которое состоит из двух точек, расположенных на прямой (концы отрезка), и точек, которые лежат между ними) на две равные части. Концы отрезка и его середину обычно обозначают латинскими буквами: A и B — концы, C — середина, C и D — концы, E — середина и т. д.
Зная координаты конца и начала отрезка, можно вычислить координаты его середины.
Пусть концы отрезка AB имеют координаты A (x₁; y₁) и B (x₂; y₂). Тогда координаты середины отрезка будут равны:
Зная координаты конца и начала отрезка, также можно вычислить расстояние, которое отделяет середину отрезка от его концов. Для этого необходимо вычислить длину отрезка по формуле:
Нахождение координат середины отрезка: примеры, решения
В статье ниже будут освещены вопросы нахождения координат середины отрезка при наличии в качестве исходных данных координат его крайних точек. Но, прежде чем приступить к изучению вопроса, введем ряд определений.
И далее мы рассмотрим, как же определять координаты середины отрезка (точки C ) при заданных координатах концов отрезка ( A и B ), расположенных на координатной прямой или в прямоугольной системе координат.
Середина отрезка на координатной прямой
Из первого равенства выведем формулу для координаты точки C : x C = x A + x B 2 (полусумма координат концов отрезка).
Полученная формула будет основой для определения координат середины отрезка на плоскости или в пространстве.
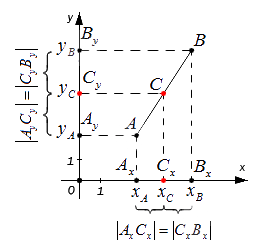
Середина отрезка на плоскости
x C = x A + x B 2 и y C = y A + y B 2
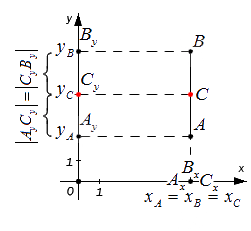
Этими же формулами можно воспользоваться в случае, когда точки A и B лежат на одной координатной прямой или прямой, перпендикулярной одной из осей. Проводить детальный анализ этого случая не будем, рассмотрим его лишь графически:
Середина отрезка в пространстве
Полученные формулы применимы также в случаях, когда точки A и B лежат на одной из координатных прямых; на прямой, перпендикулярной одной из осей; в одной координатной плоскости или плоскости, перпендикулярной одной из координатных плоскостей.
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для нахождения координат середины отрезка также можно вывести согласно алгебраическому толкованию векторов.
Следовательно, точка C имеет координаты:
По аналогии определяется формула для нахождения координат середины отрезка в пространстве:
Примеры решения задач на нахождение координат середины отрезка
Среди задач, предполагающих использование полученных выше формул, встречаются, как и те, в которых напрямую стоит вопрос рассчитать координаты середины отрезка, так и такие, что предполагают приведение заданных условий к этому вопросу: зачастую используется термин «медиана», ставится целью нахождение координат одного из концов отрезка, а также распространены задачи на симметрию, решение которых в общем также не должно вызывать затруднений после изучения настоящей темы. Рассмотрим характерные примеры.
Решение
Решение
Ответ: 58
Решение
Отрезок
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.
Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:
Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:
Свойства длин отрезков:
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:
Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:
Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.
При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):
CA > CB или CB Пример. Сравнить длину отрезков AB и AC.
Так как отрезок AB имеет большую длину, чем отрезок AC, то
Так как отрезки AB и AC имеют одинаковую длину, то
Если при измерении отрезков их длины равны, то и отрезки равны.
Середина отрезка
Середина отрезка — это точка, делящая отрезок на две равные части.
Координаты середины отрезка
Что такое середина отрезка
Отрезок — это геометрическая фигура, представляющая собой ограниченный с двух сторон участок прямой.
Пусть точки A и B не совпадают. Если провести через них прямую, то образуется отрезок AB или BA, который ограничен точками A и B. Данные точки являются концами отрезка.
Длина отрезка — это расстояние между двумя точками, ограничивающими данный отрезок. Длина отрезка AB обозначается как модуль данной геометрической фигуры, то есть |AB|.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Серединой отрезка является такая точка C, принадлежащая отрезку AB, которая расположена в центре данного отрезка, то есть |AC|=|CB|.
Правила нахождения координат середины отрезка, формулы
Середина отрезка на координатной прямой
Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа xA и xB, а точка С делит AB пополам. Определите координату xC, соответствующую С.
Так как C — это середина AB, то справедливо следующее равенство:
Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:
Опустим знак модуля и получим справедливость двух выражений:
Исходя из первого равенства, получим формулу нахождения xC, согласно которой координата точки С равна половине суммы координат A и B:
Следствием второго равенства будет следующее утверждение:
Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:
Середина отрезка на плоскости
В декартовой системе координат Oxy расположены две точки A(xA,yA) и B(xB,yB), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат xC и yC, соответствующих С.
Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат Ax, Ay; Bx, By; Cx, Cy — это проекции исходных точек.
По построению прямые AAx, BBx, CCx относительно друг друга находятся параллельно. Прямые AAy, BBy, CCy не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:
Это значит, что Cx и Cy являются серединами отрезков AxBx и AyBy соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:
Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(xA,yA) и B(xB,yB), вычисляются следующим образом:
Середина отрезка в пространстве
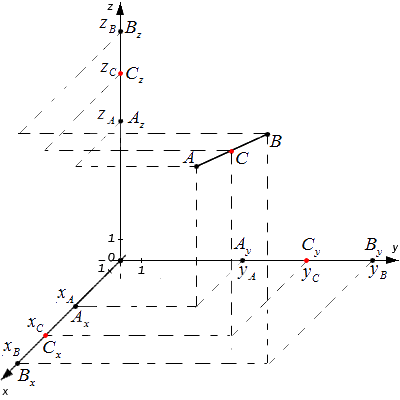
Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(xA, yA, zA) и B(xB, yB, zB). C(xC, yC, zC) — это центр АВ. Задание заключается в том, чтобы определить xC, yC, zC.
Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — Ax, Ay, Az; Bx, By, Bz; Cx, Cy, Cz — проекции точек A, B, C на них.
Воспользуемся теоремой Фалеса:
Исходя из полученных равенств следует, что Cx, Cy, Cz — делят AxBx, AyBy, AzBz пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(xA,yA,zA) и B(xB,yB,zB) используем формулу:
Метод с использованием координат радиус-векторов концов отрезка
Трактовка векторов в алгебре позволяет составить формулу для расчета координат середины отрезка.
Дано: прямоугольная система координат Oxy, в которой лежат произвольные точки A(xA,yA) и B(xB,yB), а также C, делящая пополам отрезок, ограниченный A и B.
По определению действий над вектором в геометрии:
Это значит, что С — это центр диагоналей.
Произведем подстановку в формулу (1):
Получили формулу определения координат середины отрезка, находящегося в декартовой системе координат:
По аналогично схеме можно вывести формулу для расчета координат центра отрезка, лежащего в пространстве:
Примеры решения задач
Дано: в декартовой системе координат имеются точки M(5,4) и N(1,−2). Найти координаты середины отрезка MN.
Пусть точка O — центр MN. Тогда вычислим ее координаты, подставив в формулы:
Точка O имеет координаты (3,1).
Дано: треугольник ABC лежит в прямоугольной системе координат. Известны координаты его вершин: A(7,3), B(−3,1), C(2,4). Вычислите длину медианы АМ.
Поскольку АМ является медианой треугольника ABC, то точка М делит сторону ВС на два равных отрезка, то есть является серединой отрезка ВС. Отсюда можно вычислить координат точки М:
Теперь, зная координаты начала и конца отрезка АМ, применим формулу нахождения расстояния между точками: