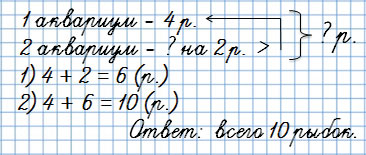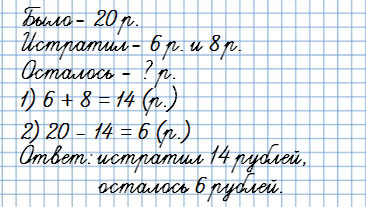Что значит решить задачу с пояснением
Что значит решить задачу с пояснением
СПОСОБЫ РЕШЕНИЯ ЗАДАЧ
Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.
С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.
Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?
Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.
Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.
Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?
Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим
Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).
Для ответа на вопрос задачи мы выполнили два действия.
Тогда количество всех рыб можно записать выражением:
По условию задачи известно, что рыбак поймал всего 10 рыб.
Значит 3 + 4 + х = 10
Решив это уравнение, мы ответим на вопрос задачи.
Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.
У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?
а) решение по действиям
Ответ: 50 книг на третьей полке.
б) по действиям с пояснением
1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.
1) Сколько книг на первой и второй полках вместе?
2) Сколько книг на третьей полке?
При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:
Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.
Например, рассмотренную выше задачу можно решить другим арифметическим способом:
В качестве арифметического способа можно рассматривать и такое решение данной задачи:
В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.
Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?
Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:
Ответ: 27 машин было в гараже
В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?
Решение задачи можно оформить так:
48 : 3 = 16 (л.) Ответ: 16 листов
[../../../_private/navbar1.htm]
Образцы оформления задачи
В разделе «Задачи» мы рассмотрели несколько видов задач. Теперь поучимся оформлять решения к ним.
В вопросе задач такого типа всегда есть «Сколько всего?»
На школьном участке ребята посадили 7 лип и 4 клёна.
Сколько всего деревьев посадили ребята?
2. Задачи на нахождение остатка
Мама с Юлей посадили 7 кустов смородины. Затем они полили 4 куста.
Сколько кустов смородины осталось полить?
Сколько грибов нашёл Володя?
У Ани было 10 рублей, а у Оли на 2 рубля меньше.
Сколько денег было у Оли?
4. Задачи на разностное сравнение
Краски стоят 15 рублей, а альбом 8 рублей.
На сколько рублей краски дороже альбома?
Дыня весит 3 кг, а арбуз 7 кг.
На сколько кг дыня легче арбуза?
5. Задачи на нахождение неизвестного слагаемого
В условии «Было. Стало. «
В вопросе «Сколько добавили?»
У Саши было 4 карандаша. Когда ему купили еще несколько карандашей, у него их стало 9.
Сколько карандашей купили Саше?
6. Задачи на нахождение неизвестного вычитаемого
В условии «Было. Осталось. «
В вопросе «Сколько уехало?»
«Сколько человек вышло?»
В гараже было 9 машин. Когда несколько машин уехало, в гараже осталось 5 машин.
Сколько машин уехало?
7. Задачи на нахождение неизвестного уменьшаемого
В условии «Убрали. Осталось. «
В вопросе «Сколько было сначала?»
После того, как Дима отдал 2 свои машинки младшему брату, у него осталось 6 машинок.
Сколько машинок было у Димы сначала?
Задачи в 2 и 3 действия
Бабушка испекла пончики и разложила их по тарелкам. На первую тарелку она положила 5 пончиков, а на вторую на вторую на 2 пончика меньше.
Сколько всего пончиков испекла бабушка?
Сколько рыбок в двух аквариумах?
У Тани было 10 тетрадей. Она использовала 4 тетради.
На сколько больше тетрадей осталось, чем Таня использовала?
У Юры было 12 счетных палочек. Для решения примеров он использовал сначала 3, а потом еще 4 палочки.
Сколько палочек у него осталось?
У Вани было 20 рублей. На покупку карандаша и ручки он истратил 6 и 8 рублей.
Сколько рублей осталось у Вани?
Задачи с составлением таблиц по из условию:
I тип:
На 3 одинаковые шторы израсходовали 18 м ткани. Сколько таких штор можно сшить из 30 м такой же ткани?
В двух одинаковых пакетах 4 кг муки. Сколько килограммов муки в пяти таких пакетах?
Задачи с составлением рисунка по условию:
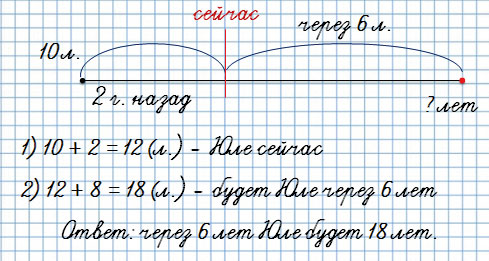
Два года назад Юле было 10 лет. Сколько лет будет Юле через 6 лет?
Поделись с друзьями в социальных сетях:
Что значит решить задачу с пояснением
IV. Список литературы.
Решениям задач уделяется достаточно много внимания в VI — IX классах средней школы. Умение решать задачи современный человек независимо от рода деятельности и уровня образования нуждается непрерывно. Без умения решать задачи нельзя обойтись ни в финансовом анализе, ни в статистике. Чтобы начислить зарплату работнику нужно знать процент налоговых отчислений; чтобы открыть депозитный счет в сбербанке мы интересуемся размером процентных начислений на сумму вклада; чтобы знать приблизительный рост цен в будущем году, мы интересуемся процентом инфляции. В торговле понятие процент используется наиболее часто: скидки, наценки, уценки, прибыль, кредит, налог на прибыль и т.д. Россию захватил «кредитный бум»: в наше время люди все чаще берут кредит на приобретение жилья, автомобиля, потребительские кредиты и кредит на образование.
Кроме того, очень часто встречаются задачи, в которых нужно уметь решать задачи не только на проценты, но и другие.
Учитывая актуальность данной темы, нами проведена данная исследовательская работа.
1.3.Гипотеза исследования – знание типов задач, и умение переводить условие задачи на умение ее решать.
Цель, предмет и гипотеза исследования обусловили выдвижение и решение следующих задач исследования:
· Изучить теоретический материал по данной теме
· Проанализировать тексты задач из учебников и задачников для средней школы.
2.3. Понятие “решение задачи ” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.
С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения В о-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.
Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?
Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.
Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?
Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим
Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).
Для ответа на вопрос задачи мы выполнили два действия.
Тогда количество всех рыб можно записать выражением:
По условию задачи известно, что рыбак поймал всего 10 рыб.
Значит 3 + 4 + х = 10
Решив это уравнение, мы ответим на вопрос задачи.
•— л —• • —л—• • —л—• • — ок —• • — ок —• • — ок —• • — ок —• • — щ —• • — щ —• • — щ —•
Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.
У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?
а) решение по действиям
Ответ: 50 книг на третьей полке.
б) по действиям с пояснением
1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.
1) Сколько книг на первой и второй полках вместе?
2) Сколько книг на третьей полке?
При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:
Например, рассмотренную выше задачу можно решить другим арифметическим способом:
В качестве арифметического способа можно рассматривать и такое решение данной задачи:
В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.
Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?
Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:
Ответ: 27 машин было в гараже
В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?
Решение задачи можно оформить так:
48 : 3 = 16 (л.) Ответ: 16 листов
Этот способ также называют «способом решения задач по вопросам».
Возникает вопрос. Сколько катер проплывет за час по озеру?
1) 48:2=24 (км/ч) скорость катера по озеру.
Возникает вопрос. Сколько катер проплывет против течения реки? Выполняется действие:
2) 46:2=23 (км/ч) скорость катера против течения реки.
Раз, у нас есть скорость катера по озеру (то есть скорость катера в стоячей воде) и скорость катера против течения реки, значит, мы можем найти скорость течения реки. Выполняется действие:
3)24-23=1 (км/ч) скорость течения реки. Пишется ответ: Ответ: 1 (км/ч).
Это способ решения задач уравнением.
Задача: мама старше Ани в 5 раз, а бабушка старше Ани в 9 раз. Вместе им 90 лет. Найдите возраст каждой
Нужно составить уравнение. Чтобы это сделать, надо написать условье составление уравнения.
Пусть х возраст Ани, тогда 5х возраст мамы и 9х возраст бабушки. Зная, что им вместе 90 лет составим и решим уравнение.
Составляем и решаем уравнение: х+5х+9х=90 15х=90 х=90:15 х=6
Мы нашли возраст Ани. Но этого нам мало, нужно найти возраст бабушки и мамы. Найдя это, мы сможем решить задачу.
Зная, что возраст мамы в 5 раз больше возраста Ани,
1) 6*5=30 (лет) возраст мамы
Зная, что возраст бабушки в 9 раз больше возраста Ани, Выполняем действие:
2) 6*9=54 (года) возраст бабушки.
Пишем ответ:
Ответ: 6 лет Ани, 30 Маме и 54 года бабушке.
Задача: на гору ведут 5 дорог. Сколькими способами можно выбрать маршрут для того, чтобы подняться в гору и затем спуститься с нее? (обратите внимание: подниматься и опускаться можно по одной и той же дороге.)
Поскольку мы знаем, что на гору и с горы ведут 5 дорог.
Считаем, сколько получилось путей. Получилось 25. Пишем ответ. Ответ: 25 маршрутов.
Такой способ очень похож на таблицу умножения.
Задача. У Васи 20 конфет, а у Димы 16. Сколько у них вместе конфет?
Составляем план таблицы:
Сверху будет количество конфет у Васи, а слева конфет у Димы.
КАК РЕШАТЬ ЗАДАЧИ
Рассмотрим план действий, который поможет понять как решать задачи.
🔴 А ТЕПЕРЬ БОЛЕЕ ПОДРОБНЕЕ:
Определите, к какому типу относится задача. Это арифметическая задача? Действия с дробями? Решение квадратных уравнений? Прежде чем приступить к решению, выясните, к какой области математики относится задача. Примеры и виды Залач. показаны ниже) Это важно, поскольку значительно упростит поиск способа решения.
Внимательно прочитайте условие задачи. Даже если задача кажется простой, внимательно изучите ее условие. Не следует приступать к решению задачи, лишь бегло ознакомившись с ее условием. Если задача сложна, вам, возможно, понадобится несколько раз перечитать ее условие, чтобы полностью понять его. Не жалейте времени на это и не приступайте к дальнейшим действиям до тех пор, пока не узнаете точно, что дано в условии и что необходимо найти.
Изложите условие задачи. Для лучшего понимания задачи полезно изложить ее условие своими словами. Можно просто пересказать условие, либо записать его в том случае, если вам неудобно говорить вслух (например, на экзамене). Сравните собственное изложение задачи с ее первоначальным условием, выяснив тем самым, правильно ли вы поняли задание.
Изобразите задачу графически. Если вы считаете, что это поможет, представьте задачу графически — возможно, так легче будет определить дальнейшие действия. Необязательно создавать подробную схему, достаточно набросать условие задачи в общих чертах, указав численные значения. При создании схемы справляйтесь с условием задачи, по окончании сравните готовое изображение с условием еще раз. Задайте самому себе вопрос: «Верно ли мой рисунок отображает задачу?» Если да, можно приступить к решению задачи. Если же ответ отрицателен, перечитайте условие еще раз.
Изучите структуру задачи. Внимательно прочитав условие, вы, возможно, вспомните похожие задачи, решенные вами ранее. Можно построить таблицу с внесенными в нее данными, которая поможет вам определить характер задачи. Отметьте выявленные характерные черты задачи — они помогут вам при ее решении. Не исключено даже, что вы вспомните схожие задачи и сразу получите ответ.
Составление плана решения
Потренируйтесь на более легкой задаче. Если есть более простая задача, похожая на ту, которую необходимо решить, попробуйте свои силы сначала на ней. Предварительный разбор простой задачи, в которой используются те же приемы и формулы, облегчит решение более сложного задания.
Сделайте обоснованное предположение о том, каким должен быть ответ. Прежде чем приступать к непосредственному решению задачи, попытайтесь оценить ответ. Определите величины и другие факторы, влияющие на оценку. Проверьте свои рассуждения, не упустили ли вы чего-либо из виду.
Решение задачи
Придерживайтесь составленного плана. Выполняйте этапы последовательно в том порядке, в котором вы наметили их ранее. Чтобы избежать ошибок, перепроверяйте результат, полученный на каждом этапе.
Сравнивайте полученные результаты с предварительно сделанными оценками. По завершении каждого этапа полезно сравнить его результат со сделанными ранее оценками; сопоставьте также конечный ответ с его предварительной оценкой. Задайте себе вопрос: «Близки ли мои предположения к полученным результатам?» Если ответ отрицателен, подумайте, почему. Проверьте полученные результаты, просмотрев все шаги решения еще раз
Попробуйте другую схему решения. Если составленный вами план не сработал, вернитесь к этапу планирования и разработайте новый план. Не расстраивайтесь в случае неудачной попытки, учеба не обходится без ошибок — наоборот, вы научитесь на своих ошибках и сможете избежать их в дальнейшем. Выявите сделанные ошибки и продолжайте работу. Не зацикливайтесь на ошибках и не огорчайтесь из-за них.
Проанализируйте задачу. Получив правильный ответ, вернитесь к началу и просмотрите решение еще раз. Анализ задачи и ее решения поможет вам в следующий раз, когда вы столкнетесь с подобной задачей. Также вы лучше усвоите использованные методы и приемы, которые обязательно пригодятся вам в дальнейшем
Советы
Какие бывают математические задачи:
ПРОСТЫЕ И СОСТАВНЫЕ ЗАДАЧИ
Простые Математические Задачи состоят из 5 частей:
Обязательно в задаче нужно выявлять ОПОРНЫЕ СЛОВА, ОПОРНЫЕ СЛОВА — это основа краткой записи, их нужно уметь находить для определения главного в задаче.
В вазе 3 белых и 2 розовых гвоздики.
Сколько всего гвоздик в вазе?
В указанной задаче:
Второе опорное слово — розовые, которое в первом классе, сокращаем словом Р, но начиная со 2 класса- Роз.
Третье опороное слово всегда содержится в вопросе.
В данной задаче третье опорное слово — всего, которое в краткой записи заменяется фигурной скобкой с вопросом посередине
Ответ: 5 гвоздик всего в вазе.
Простые задачи решаются одним действием.
Составные задачи решаются двумя и более действиями, разными способами.
У Иры 3 куклы, что в 2 раза меньше, чем у Светы. Сколько кукол у обеих девочек?
• по действиям с пояснениями
1) 3 • 2 = б (к.) — у Светы
2) 3 + 6 = 9 (к.) — у обеих девочек
• по действиям с вопросами
1. Сколько кукол у Светы? 3-2 = б(к.)
2. Сколько кукол у обеих девочек? 3 + 6 = 9 (к.)
Ответ: у обеих девочек 9 кукол.
ЗАДАЧИ НА НАХОЖДЕНИЕ СУММЫ
первое второе сумма
Чтобы найти сумму, надо сложить слагаемые
У балалайки 3 струны, а у контрабаса — 4. Сколько всего струн у этих музыкальных инструментов?
Решение: 3 + 4 = 7 (с.) Ответ: у этих музыкальных инструментов 7 струн.
У Кати 3 книги, что на 2 книги меньше, чем у Иры. Сколько всего книг у девочек?
Решение: 1)3 + 2 = 5 (к.)-у Иры 2) 3 + 5 = 8 (к.) — всего Ответ: всего у девочек 8 книг.
уменьшаемое вычитаемое разность
Чтобы найти разность, надо из уменьшаемого вычесть вычитаемое
У кошки родилось 6 котят. Четырёх котят отдали. Сколько котят осталось?
Решение: 6-4 = 2 (к.) Ответ: осталось 2 котёнка.
У Маши было 4 конфеты. Бабушка дала ей ещё 8 конфет. После обеда девочка съела 3 конфеты. Сколько конфет осталось у Маши?
1) 4 + 8 = 12 (к.) — было у Маши до обеда
2) 12 — 3 = 9 (к.) — осталось после обеда Ответ: у Маши осталось 9 конфет.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО УМЕНЬШАЕМОГО
уменьшаемое вычитаемое разность
Чтобы найти уменьшаемое, надо к разности прибавить вычитаемое
Когда Вася решил 15 примеров, ему осталось решить ещё 11 при меров. Сколько всего примеров нужно решить Васе?
Решение: 15+ 11 = 26 (п.) Ответ: Васе нужно решить 26 примеров.
Мама решила связать новый шарф. Каждый день в течение неде ли она вязала по 20 см. Какой длины должен получиться шарф, если ей осталось связать ещё 10 см?
1. 20 • 7 = 140 (см) — мама связала за неделю
2. 140 + 10 = 150 (см) — длина шарфа Ответ: шарф должен получиться длиной 150 см.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ВЫЧИТАЕМОГО И СЛАГАЕМОГО
Чтобы найти неизвестное вычитаемое, надо из уменьшаемого вычесть разность
Чтобы найти неизвестное слагаемое, надо из суммы вычесть известное слагаемое
В журнале 45 страниц, а в книге 155 страниц. На сколько страниц в книге больше, чем журнале?
Решение: 155-45 = 110 (стр.) Ответ: в книге на 110 страниц больше.
Катя собрала 12 больших ромашек и 7 маленьких. Несколько ромашек она подарила бабушке, и у девочки осталось 10. Сколько ромашек Катя подарила бабушке?
1. 12 + 7 = 19 (ром.) — собрала Катя
2. 19 — 10 = 9 (ром.) — подарила бабушке Ответ: 9 ромашек Катя подарила бабушке.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ И УИЕНЬШЕНИЕ ЧИСЛА НА НЕСКОЛЬКО ЕДИНИЦ
Увеличить на… значит прибавить к числу несколько единиц
5 увеличить на 2 = 5 + 2
Уменьшить на значит вычесть из числа несколько единиц
5 уменьшить на 2 = 5 — 2
Новорождённый котёнок весит 100 г, а трёхнедельный — на 200 г больше. Сколько весит трёхнедельный котёнок?
Решение: 100 + 200 = 300 (г) Ответ: трёхнедельный котёнок весит 300 г.
Петя купил 15 шоколадок, а Юра на 3 шоколадки меньше. Сколько шоколадок купил Юра?
Решение: 15-3 = 12 (ш.) Ответ: Юра купил 12 шоколадок
ЗАДАЧИ НА НАХОЖДЕНИЕ ПРОИЗВЕДЕНИЯ
первый множитель второй множитель произведение
Чтобы найти произведение, надо перемножить множители
У котёнка 4 лапы. Сколько лап у пятерых котят?
Решение: 4 • 5 = 20 (л.) Ответ: у пятерых котят 20 лап.
С первого куста смородины собрали 3 кг ягод, со второго — 4 кг, а с третьего — в 2 раза больше, чем с первого и со второго вместе. Сколько килограммов смородины собрали с третьего куста?
1. 3 + 4 = 7 (кг) — собрали с двух кустов
2. 7 • 2 = 14 (кг) —собрали с третьего куста Ответ: с третьего куста собрали 14 кг смородины.
ЗАДАЧИ НА НАХОЖДЕНИЕ ЧАСТНОГО
делимое делитель частное
Чтобы найти частное, надо делимое разделить на делитель
У мамы было 10 мандаринов. Она раздала двум дочкам мандарины поровну. Сколько мандаринов получила каждая девочка?
Решение: 10 : 2 = 5 (м.) Ответ: каждая девочка получила 5 мандаринов.
Бабушка сварила варенье: 9 литров малинового и б литров клубничного. Всё варенье она разлила в трёхлитровые банки. Сколько банок с вареньем получилось?
1. 9 + б = 15 (л) — всего варенья сварила бабушка
2. 15 : 3 = 5 (б) — всего банок Ответ: получилось 5 банок с вареньем.
Задачи на нахождение неизвестного делимого
делимое делитель частное
Чтобы найти делимое, надо частное умножить на делитель
За 2 дня учительнице надо проверить тетради учеников. Она со бирается проверять по 14 тетрадей вдень. Сколько всего тетрадей надо проверить?
Решение: 14 • 2 = 28 (т.) Ответ: всего надо проверить 28 тетрадей.
Переводчик в течение недели переводил по 6 страниц в день. Ему осталось перевести ещё 4 страницы. Сколько всего страниц он перевёл?
1. 6 * 7 = 42 (стр.) — перевёл за неделю
2. 42 + 4 = 46 (стр.) — всего
Ответ: 46 страниц перевёл переводчик.
ЗАДАЧИ НА НАХОЖДЕНИЕ НЕИЗВЕСТНОГО ДЕЛИТЕЛЯ И МНОЖИТЕЛЯ
Чтобы найти неизвестный делитель, надо делимое разделить на частное
Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель
Витя собирает марки. Папа подарил ему 20 марок, а дедушка — 15 марок. Все марки Витя разложил в альбом, на 5 страниц поровну. Сколько марок на каждой странице?
1. 20 + 15 = 35 (м.) — всего у Вити
2. 35 : 5 = 7 (м.) — на каждой странице Ответ: на каждой странице по 7 марок.
ЗАДАЧИ НА УВЕЛИЧЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ И МЕНЬШЕНИЕ
Увеличить в… раз значит умножить число
3 увеличить в 2 раза =3-2
Уменьшить в… раз значит разделить число
6 уменьшить в 2 раза = 6:2
Маме 30 лет, а бабушка — в 2 раза старше. Сколько лет бабушке?
Решение: 30 • 2 = 60 (л.) Ответ: бабушке 60 лет.
Масса белого медведя 900 кг, а масса медведицы — в 3 раза меньше. Какова масса медведицы?
Решение: 900 : 3 = 300 (кг) Ответ: масса медведицы 300 кг.
ЗАДАЧИ НА РАЗНОСТНОЕ СРАВНЕНИЕ
Чтобы узнать, на сколько одно число больше или меньше другого, надо из большего числа вычесть меньшее
* На сколько 10 больше, чем 5? 10 — 5 = 5; 10 больше, чем 5, на 5
* На сколько 10 меньше, чем 15? 15 — 10 = 5; 10 меньше, чем 15, на 5
В классе 15 мальчиков и 12 девочек. 22 человека посещают школу, а остальные болеют. На сколько меньше болеющих учеников, чем посещающих школу?
1. 15 + 12 = 27 (чел.) — учатся в классе
2. 27 — 22 = 5 (чел.) — болеют
3. 22 — 5 = 17 (чел.) — на сколько меньше Ответ: болеющих учеников на 17 меньше, чем посещающих школу.
Чтобы узнать, во сколько раз одно число больше или меньше другого, надо большее число разделить на меньшее
• Во сколько раз 10 больше, чем 5? 10 : 5 = 2; 10 больше, чем 5, в 2 раза
• Во сколько раз 5 меньше, чем 15? 15 : 5 = 3; 5 меньше, чем 15, в 3 раза
Машинка стоит 90 рублей, а шоколадка — в 3 раза дешевле. Сколько стоят машинка и шоколадка вместе?
1. 90 : 3 = 30 (руб.) — стоит шоколадка
2. 90 + 30 = 120 (руб.) — стоят вместе Ответ: машинка и шоколадка стоят 120 рублей.
ЗАДАЧИ НА ДЕЛЕНИЕ ПО СОДЕРЖАНИЮ
Фрукты разложили на тарелки, по 4 штуки на каждую. Сколько по надобилось тарелок?
Понадобилось 2 тарелки
Бабушка раздала внукам 15 яблок, по 5 штук каждому. Сколько Внуков у бабушки?
Решение: 15 : 5 = 3 (внуков) Ответ: у бабушки 3 внука.
ЗАДАЧИ НА ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ
Детям раздали конфеты поровну. Сколько детей получило конфеты?
Двое детей получили конфеты
Для подготовки школьного спектакля учительница разделила 30 учеников на 5 групп. Сколько учеников в каждой группе?
Решение: 30 : 5 = 6 (уч.) Ответ: в каждой группе по 6 учеников.