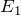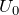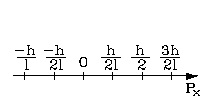Что значит решить уравнение шредингера
Уравнение Шредингера в квантовой физике
Обновлено: 19 Июля 2021
Уравнение Шредингера имеет большое значение для квантовой механики — наряду со вторым законом Ньютона в классической механике или уравнением Максвелла для изучения природы электромагнитных волн. Закономерности, описанные ученым, объясняют движение частиц, скорость которых существенно меньше, чем скорость света.
Общее уравнение Шредингера — какой имеет вид и зачем нужно
Уравнением Шредингера называют линейное дифференциальное равенство с частными производными, которое описывает изменение в пространстве и во времени чистого состояния посредством волновой функции в гамильтоновых квантовых системах.
Опытным путем можно наблюдать волновые свойства частиц. Определение данного явления является следствием уравнения, которое описывает движение микроскопических частиц в разных силовых полях. Закономерности движения в квантовой механике вытекают из статистического толкования волн де Бройля и соотношения неопределенностей Гейзенберга.
Главное уравнение представляет собой формулу относительно волновой функции \(\psi\) (x, y, z,t). Это объясняется тем, что \(\left|\psi \right|\) является определением вероятности присутствия частицы в определенное время t в объеме ΔV, то есть в области со следующими координатами:
Основная закономерность нерелятивистской квантовой механики была представлена в 1926 году Э. Шредингером. Данная формула не является выводом, это — постулат. Справедливость уравнения подтверждается согласием с результатами опыта, что говорит о природном характере выявленной закономерности.
Общее уравнение Шредингера обладает следующим видом:
где ħ равно отношению \(\frac
m — является массой частицы,
Δ — оператор Лампаса,
i — представляет собой мнимую единицу,
U(x, y, z, t) — равно потенциальной функции частицы в силовом поле, в котором она движется,
\(\psi\) (x, y, z, t) — служит искомой волновой функцией частицы.
Данная формула справедлива для любых частиц, спин которых равен нулю, движущихся с небольшой скоростью относительно скорости света. Уравнение можно дополнить условиями, характерными для волновой функции:
В первом случае описано уравнение, которое зависит от времени. Многие физические явления, наблюдаемые в микромире, можно охарактеризовать с помощью упрощенной формулы. При исключении зависимости волновой функции от времени можно определить закономерность Шредингера для стационарных состояний, то есть состояний, в которых значения энергии фиксированы. Такие ситуации возможны при стационарном силовом поле, в котором происходит движение частицы. Таким образом, функция U = U (x, y, z) не определяется временем и обладает смыслом потенциальной энергии.
В данном случае уравнение Шредингера будет иметь следующий вид:
\(\Delta \psi +\frac<2m>
Данная формула получила название уравнения Шредингера для стационарных состояний. Здесь используют полную энергию Е-частицы. Согласно теории дифференциальных уравнений доказано, что имеется бесчисленное множество решений подобных уравнений, которые имеют физический смысл при отборе методом наложения граничных условий. В случае уравнения Шредингера такими условиями являются характеристики регулярности волновых функций:
Применение уравнения Шредингера
Уравнение Шредингера не подходит для описания следующих явлений:
Можно рассмотреть применение уравнения Шредингера к свободной частице или электрону, который совершает движение вдоль оси ОХ. При этом величина потенциальной энергии частицы, находящейся в свободном движении, равна нулю. То есть U = 0. Тогда уравнение Шредингера будет иметь следующий вид:
Исходя из гипотезы Бройля, можно смоделировать перемещение такого микроскопического объекта с помощью плоской монохроматической волны, занимающей все пространство:
Волновая функция, характеризующая движение свободной частицы вдоль оси ОХ, бедт записана следующим образом:
где \(\psi _<0>\) является амплитудой волны.
Круговая частота \(\omega\) и волновое число k связаны с полной энергией E и импульсом р следующими закономерностями:
Из данных соотношений следует:
В таком случае волновая функция будет иметь следующий вид:
Продемонстрировать соответствие данного вида функции уравнению Шредингера можно, если определить \(\Delta \psi\) и \(P^<2>\)
Далее необходимо определить \(\frac
Используя отношение энергии частицы Е к импульсу p, получим формулу:
Подставив данные значения в уравнение, можно вывести следующее равенство:
Данное равенство соответствует уравнению Шредингера, когда U=0. Корректный вид волновой функции можно обосновать для случая движения частицы в силовом поле, в случае, когда потенциальная энергия не равна нулю. Формула будет иметь следующий вид:
Такое уравнение характеризует энергию движения частицы по аналогии с кинетической энергией в классической механике. После подстановки значений Е и Р уравнение приобретает следующий вид:
Конечная формулировка идентична уравнению Шредингера. Данное выражение применимо для частицы, которая совершает движение в силовом поле.
Пример решения уравнения Шредингера
Задание 1
Электрон движется в одном измерении вдоль оси ОХ между двумя потенциальными барьерами. В случае, если высота барьеров на концах ямы не имеет ограничений, электрон, как и в атоме, совершает финитное движение. Необходимо описать движение в квантовой механике и поведение импульса и энергии частицы.
Решение
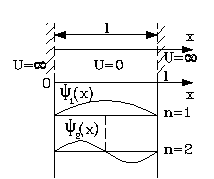
Вначале следует изобразить ситуацию схематично
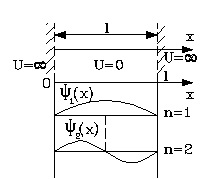
Согласно условиям задачи, функция U(x) обладает особым, разрывным видом и равна нулю в области между стенками. На краях ямы, то есть на ее барьерах, функция будет бесконечна:
При х=0 и х=l \(U=\propto\)
Уравнение Шредингера для стационарных состояний частиц, находящихся между барьерами, имеет следующий вид:
Выполняя преобразования в формулах, получим:
К полученной формуле следует прибавить граничные условия на барьерах ямы. Необходимо учесть связь волновой функции и вероятности нахождения частиц. Согласно условиям задания, частица за пределами стенок не находится. В таком случае значение волновой функции на стенках и за их пределами равно нулю. Граничные условия задания будут иметь следующий вид:
При дальнейших действиях нужно учитывать, что решением последней формулы являются волны де-Бройля. Одну волну де-Бройля в качестве решения к задаче не применить, так как с ее помощью заранее описывается свободная частица, движущаяся в одном направлении. В данном случае рассматривается движение частицы между стенками. Поэтому, используя принцип суперпозиции, в решении можно применить две волны де-Бройля, совершающих движение навстречу друг к другу с импульсами р и –р. Формула будет иметь следующий вид:
\(\psi =C_<1>\times exp\left(\frac
Исходя из первых граничных условий:
Решение задачи будет иметь следующий вид:
\(\psi =C\times \left(exp\left(\frac
\(exp\left(\frac
Постоянная А выходит из условий нормировки. В данном случае она не представляет интереса. Необходимо использовать второе граничное условие. Тогда решение можно записать в виде уравнения:
Импульс при этом принимает только определенные значения:
Следует учесть, что n не равно нулю. Это объясняется тем, что в противном случае волновая функция повсюду имела нулевые значения. В этом случае для частицы между стенками состояние покоя не характерно. Электрон обязательно должен совершать движение. Минимальное значение возможного импульса движущейся частицы равен:
Ранее было указано, что импульс электрона изменяет знак во время отражения от барьеров. В этом заключается сложность представления ответа на вопрос, каков импульс у частицы, запертой между стенками. Он может быть равен –р или +р. Импульс не определен. Степень неопределенности будет выражаться в следующем:
Неопределенность координаты Δх равна l. Обнаружить частицу можно в пределах между барьерами. Точное местонахождение электрона неизвестно. Наименьшее значение импульса имеет вид:
Исходя из этого условия, можно вывести равенство:
\(\Delta x\times \Delta p_
Таким образом, соотношение Гейзенберга в рамках данной задачи, то есть при наличии наименьшего значения р, подтверждено. В случае произвольно-возможного значения импульса соотношение неопределенности приобретает такой вид:
\(\Delta x\times \Delta p_
Согласно исходному постулату Гейзенберга-Бора о неопределенности Δх и Δу, установлена лишь нижняя граница неопределенностей, возможная при измерениях. В начале движения наблюдают минимальные неопределенности, которые возрастают со временем. Полученное уравнение демонстрирует следующее: импульс системы в квантовой механике не всегда изменяется непрерывно. Спектр импульса электрона в данном случае дискретный, импульс частицы между барьерами изменяется скачкообразно. Величина такого скачка при условиях задания является постоянной величиной и определяется как:
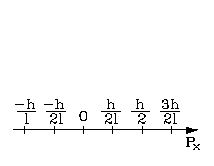
Можно изобразить спектр возможных значений импульса электрона. Дискретность изменения механических величин, не применимая к классической механике, в квантовой механике является следствием ее математического аппарата. Невозможно представить наглядное объяснение скачкообразного изменения импульса. Это закон квантовой механики, данный вывод следует из него логически и является объяснением.
Далее необходимо обратиться к энергии электрона. Данная величина обладает связью с импульсом. В случае дискретного спектра импульса получают дискретный спектр значений энергии частицы между барьерами. Подставив ранее известные формулы в уравнение, получим:
где n = 1, 2,…, представляет собой квантовое число.
Таким образом, получают энергетические уровни.
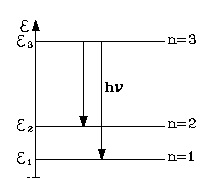
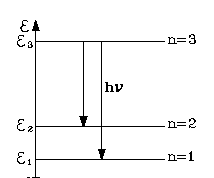
На рисунке представлены энергетические уровни, согласно условию задания. Если изменить их, то схема расположения энергетических уровней будет изменена. В случае, когда частица обладает зарядом, как электрон, и расположена на самом низком энергетическом уровне, она будет в состоянии спонтанно испускать свет, как фотон. При этом переход на более низкий энергетический уровень возможен с условием:
Для этого задания волновые функции, характерные каждому стационарному состоянию, являются синусоидами. Их нулевые значения будут отмечены на стенках.
Уравнение Шредингера имеет огромное значение для развития современной науки. Квантовая механика является популярной дисциплиной для изучения в специализированных вузах. Нередко студенты учебных заведений сталкиваются со сложными задачами, решение которых отыскать порой достаточно сложно.
При возникновении трудностей в образовательном процессе получить квалифицированную помощь можно с помощью сервиса Феникс.Хелп.
Уравнение Шрёдингера
Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.
Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.
Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.
Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):
где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.
Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.
Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.
Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).
Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.
Уравнение Шредингера
Принципы квантовой механики
Состояние частицы задается двумя величинами: координатами (радиус-вектором) и импульсом. В рамках квантовой механики ставить вопрос о точном местоположении, траектории частицы не корректно. Для квантовой частицы координаты и импульс могут быть неопределёнными. Поэтому ее состояние задается двумя вероятностными функциями:
Первая характеризует неопределённые координаты частицы, вторая — неопределённые импульсы. Вместо двух указанных функций W и V в квантовой механике вводится одна, комплексная функция, называемая волновой функцией. (Комплексная функция равносильна двум функциям, т.к. состоит из двух частей: действительной и мнимой.) Достоинством такого метода является в первую очередь то, что действительная и мнимая части волновой функции являются функциями не различных переменных (х и 



Уравнение Шредингера
Уравнение же связанной частицы, на которую действуют силы, удобнее получить в координатном представлении. Нужно сказать, что в квантовой механике, строго говоря, нельзя ввести понятие силы, как нельзя ввести понятие скорости. И это ясно, если вспомнить, что по определению сила есть производная от импульса частицы по времени. Импульс же квантовой частицы является неопределённым, и его невозможно продифференцировать по времени. Поэтому взаимодействие частиц в квантовой механике характеризуют не силой, а потенциальной энергией.
Движение связанной частицы массы m будет задаваться уравнением следующего вида:
где 
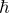
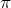
Это уравнение называется временным уравнением Шредингера.
Если 
где E-полная энергия квантовой системы, а 
Уравнение Шредингера является основным уравнением движения частицы в квантовой механике. Оно не может быть выведено из других соотношений. Его следует рассматривать как исходное основное предположение, справедливость которого подтверждается тем, что все следствия из него вытекающие, подтверждаются опытами.
Решение уравнения Шредингера
С математической точки зрения — это дифференциальное уравнение в частных производных. Уравнение в частных производных имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи.
С физической точки зрения нужно отметить, что согласно уравнению Шредингера волновая функция изменяется детерминировано, то есть совершенно однозначно. В этом смысле квантовая механика напоминает классическую, в которой движение системы заранее предопределено начальными условиями. Однако сама волновая функция имеет вероятностный смысл. Можно сказать, в квантовой механике детерминировано изменяются вероятности, а не сами физические события. События же всегда случайны и совершаются непредсказуемо.
Наконец, необходимо отметить еще одну очень важную особенность уравнения Шредингера: оно линейно. Волновая функция и ее производные входят в него в первой степени и для волновых функций справедлив принцип суперпозиции. Он в квантовой механике играет очень важную роль, так как позволяет сложные движения раскладывать на более простые движения. Например, движение свободной частицы выражается отнюдь не только волнами де-Бройля. Возможны более сложные выражения для результирующих волновых функций той же свободной частицы. Вместе с тем согласно принципу суперпозиции любое сложное движение свободной частицы можно представить как сумму волн де-Бройля.
Уравнение Шредингера является математическим выражением корпускулярно-волнового дуализма микрочастиц. В предельном случае, когда длины волн де Бройля значительно меньше размеров рассматриваемого движения уравнение Шредингера позволяет описывать движение частиц по законам классической механики.
Тогда как с точки зрения математики уравнение Шредингера – это волновое уравнение, по структуре подобно уравнению колебания струны. Однако, решения уравнения Шредингера 
Физический смысл имеет модуль произведения 
w — определяется как плотность вероятности нахождения частицы в точке пространства,
где 

где W – вероятность нахождения частицы в объеме V.
Из вероятностного смысла волновой функции следует, что квантовая механика имеет статистический характер. С помощью волновой функции, которая является решением уравнения Шредингера нельзя точно описать траекторию движения квантовой частицы, можно лишь сказать какова вероятность обнаружить эту частицу в разных областях пространства.
Примеры решения задач
| Задание | Рассмотрите движение электрона в одном измерении (по оси х) между двумя потенциальными барьерами. Допустим, что высота барьеров на концах ямы бесконечна. Электрон, как и в атоме, совершает финитное движение. Как оно описывается в квантовой механике? Как ведет себя импульс и энергия частицы? |
| Решение | Сделаем рисунок |
В нашей задаче функция U(x) имеет особый, разрывный вид: она равна нулю между стенками, а на краях ямы (на стенках) обращается в бесконечность:
При x = 0 и 

Будем считать импульс электрона по модулю определённым, и постоянным, но каждый раз изменяющим знак пpи отражении от стенки. Энергия электрона связана с импульсом формулой:
Запишем уравнение Шредингера для стационарных состояний частиц в точках расположенных между стенками:
или, если учесть формулу (1.1)
К уравнению (1.3) необходимо добавить граничные условия на стенках ямы. Примем во внимание, что волновая функция связана с вероятностью нахождения частиц. Кроме того, по условиям задачи за пределами стенок частица не может быть обнаружена. Тогда волновая функция на стенках и за их пределами должна обращаться в нуль, и граничные условия задачи принимают простой вид:
Постоянные 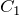
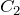
Согласно первому граничному условию имеем:
Таким образом, получим решение нашей задачи:
Как известно, 
Постоянная А определяется из условия нормировки. Но здесь не она представляет особый интерес. Осталось неиспользованным второе граничное условие. Какой результат оно позволяет получить? Применительно к найденному решению (1.5) оно приводит к уравнению:
Из него видим, что в нашей задаче импульс p может принимать не любые значения, а только значения
Кстати, n не может равняться нулю, так как волновая функция тогда бы всюду на промежутке (0…l) равнялась нулю! Это означает, что частица между стенками не может находиться в покое! Она обязательно должна двигаться. В аналогичных условиях находятся электроны проводимости в металле. Полученный вывод распространяется и на них: электроны в металле не могут быть неподвижными.
Наименьший возможный импульс движущегося электрона равен
Мы подтвердили соотношение Гейзенберга в условиях нашей задачи, то есть при условии существования наименьшего значения p. Если же иметь в виду произвольно-возможное значение импульса, то соотношение неопределённости получает следующий вид:
Это означает, что исходный постулат Гейзенберга-Боpа о неопределённости 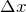

Однако формула (1.6) указывает и на другой чрезвычайно интересный вывод: оказывается, импульс системы в квантовой механике не всегда в состоянии изменяться непрерывно (как это всегда имеет место в классической механике). Спектр импульса частицы в нашем примере дискретный, импульс частицы между стенками может изменяться только скачками (квантами). Величина скачка в рассмотренной задаче постоянна и равна 
На рис. 2. наглядно изображён спектр возможных значений импульса частицы. Таким образом, дискретность изменения механических величин, совершенно чуждая классической механике, в квантовой механике вытекает из ее математического аппарата. На вопрос, почему импульс изменяется скачками, наглядного найти нельзя. Таковы законы квантовой механики; наш вывод вытекает из них логически — в этом все объяснение.
Обратимся теперь к энергии частицы. Энергия связана с импульсом формулой (1). Если спектр импульса дискретный, то автоматически получается, что и спектр значений энергии частицы между стенками дискретный. И он находится элементарно. Если возможные значения 
где n = 1, 2,…, и называется квантовым числом.
Таким образом, мы получили энергетические уровни.
Рис. 3 изображает расположение энергетических уровней, соответствующее условиям нашей задачи. Ясно, что для другой задачи расположение энергетических уровней будет иным. Если частица является заряженной (например, это электрон), то, находясь не на низшем энергетическом уровне, она будет в состоянии спонтанно излучать свет (в виде фотона). При этом она перейдёт на более низкий энергетический уровень в соответствии с условием:
Волновые функции для каждого стационарного состояния в нашей задаче представляют собой синусоиды, нулевые значения которых обязательно попадают на стенки. Две такие волновые функции для n = 1,2 изображены на рис. 1.
| Задание | Квантовая частица заперта в потенциальной прямоугольной одномерной яме конечной глубины. Найти энергетический спектр частицы. |
Функция 


Это означает, что задачу надо решать для трех областей поочерёдно. Единство функции 

Задача обладает симметрией, достаточно будет рассмотреть одну ее половину. Например найти 
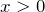

Рассмотрим область I. Для нее уравнение (2.2.) имеет вид:

Полученное уравнение есть аналог уравнения гармонических колебаний. Сразу запишем его
Рассмотрим область II. Для нее уравнение (2.2) имеет вид:
Перепишем его следующим образом:


Будем искать решение в виде
Подставим эту функцию в уравнение 2.10. Получим:


То есть функция 

Общее решение уравнения (2.10) получается:
Используем условие для волновой функции на бесконечности. Второе слагаемое в уравнении 2.12. представляет собой функцию, растущую с ростом x. Значит, следует положить 
Окончательно запишем для области II:
Используем условия «сшивания». Перепишем их с учетом формул 2.8., 2.13.
Целесообразно начало координат перенести в точку x=a, тогда условия (2.14) будут выглядеть проще при x=0:
отсюда следует, что 
Постоянную A найдем из условий нормировки.
Если квантовая частица движется в замкнутой области, то ее энергетический спектр дискретный. А если спектр дискретен, то энергию частицы нельзя задать, не определив ее возможных значений.
Для того, чтобы найти спектр энергии используем то, что задача обладает симметрией. Это значит, что посередине потенциальной ямы плотность вероятности должна иметь экстремум. Соответственно, первая производная ее в точке x=-a равна 0. Используем это условие:

отсюда 
или 
где n- квантовое число, n=1,2,3…k
Тогда
Найдем не весь спектр энергии, а только часть ее, соответствующую условию
В этом случае тангенс угла совпадает с аргументом.
подставим в 2.22 значения 
Если 


Отсюда энергетический спектр при данном ограничении примет вид:


Минимальная энергия частицы определяется соотношением:
Наше соотношение выполняется при выполнении следующих условий:
откуда следует, что


Полученное условие обозначает, квадратный корень из значения