Что значит решить треугольник
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
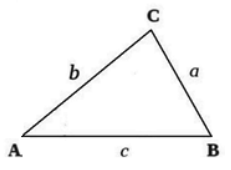
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
 |
 |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения
Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
  . . |
  . . |
 , ,  . . |
И, наконец, находим угол C:
  |
Решение треугольника по двум сторонам и углу между ними
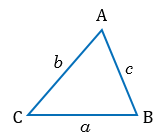
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
 |
Найдем сторону c используя теорему косинусов:
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:
Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:
   . . |
Из формулы (3) найдем cosA:
  |
Поскольку уже нам известны два угла то находим третий:
  . . |
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
 |
Так как, уже известны два угла, то можно найти третий:
Далее, для находждения сторон b и c воспользуемся тероемой синусов:
 , ,  . . |
 , ,  . . |
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
  |
Найдем сторону b. Из теоремы синусов имеем:
 |
 |
Найдем сторону с. Из теоремы синусов имеем:
Решение треугольников
Вы будете перенаправлены на Автор24
Предварительные сведения
Рисунок 1. Треугольник
Примеры задач на решение треугольников
Из определения мы видим, что если в треугольнике даны три каких-либо элемента треугольника, то его можно разрешить, то есть найти остальные три элемента этого треугольника. Будем рассматривать решение треугольника на примерах задач.
Решение.
Найдем сначала третью сторону по теореме косинусов:
Используя вновь теорему косинусов, имеем:
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle B=<180>^0-\angle A-\angle C\]
\[\angle A=arc\ cos\left(\frac
Решение.
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle A=<180>^0-\angle B-\angle C\]
По теореме синусов, имеем:
Готовые работы на аналогичную тему
Решение.
Найдем сначала один из углов по теореме косинусов:
Используя вновь теорему косинусов, имеем:
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle B=<180>^0-\angle A-\angle C\]
\[\angle A=arc\ cos\left(\frac
Решение.
По теореме синусов, имеем
По теореме о сумме углов треугольника, получаем:
\[\angle A+\angle B+\angle C=<180>^0\] \[\angle C=<180>^0-\angle B-\angle A\]
По теореме косинусов, имеем:
Получи деньги за свои студенческие работы
Курсовые, рефераты или другие работы
Автор этой статьи Дата последнего обновления статьи: 11 04 2021
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение треугольников.
Решением треугольника называется нахождение всех его шести элементов (т.е. трех сторон и трех углов) по каким-нибудь трем данным элементам, определяющим треугольник.
Эта математическая программа находит сторону \( c \), углы \( \alpha \) и \( \beta \) по заданным пользователем сторонам \( a, b \) и углу между ними \( \gamma \)
Программа не только даёт ответ задачи, но и отображает процесс нахождения решения.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Введите стороны \( a, b \) и угол между ними \( \gamma \) Решить треугольник
Двойкам нет
Решение треугольников
Решить треугольник — значит по известным его сторонами и углами найти неизвестные его стороны и углы.
Задачи на решение треугольников подразделяются на следующие виды:
1. Решение треугольника по известным стороной и двумя углами.
— Находим третий угол треугольника, учитывая, что сумма всех внутренних углов треугольника равна 180 °.
— Записываем теорему синусов для этого треугольника и, выбирая попарно соотношение сторон и противоположных них углов, находим две другие стороны треугольника.
2. Решение треугольника по известным двум сторонам и углу между ними.
— По теореме косинусов находим третью сторону.
— За следствием из теоремы косинусов находим косинусы неизвестных углов треугольника, а по возможности и сами углы.
Обратите внимание!
Это можно сделать и с помощью теоремы синусов.
3. Решение треугольника по известным двумя сторонами и углом, противоположным одной из них.
— По теореме синусов находим угол, противоположный ко второй известной стороны. При этом обратите внимание, что одному и тому же значению синуса угла соответствуют два угла — острый и тупой, смежный с этим острым углом. Учитывайте, что против большей стороны лежит больший угол.
— Находим третий угол треугольника.
— По теореме синусов находим третью сторону треугольника.
Обратите внимание! Эта задача может иметь два решения.
4. Решение треугольника по известным трем сторонам.
— За следствием из теоремы косинусов находим один из углов треугольника.
— По теореме синусов находим два других угла треугольника.
Решение треугольников
Введем обозначения для сторон 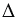
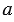
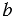
Далее рассмотрим задачи на решение треугольников с использованием данных обозначений.
Задача 1
| Решение треугольника по двум сторонам и углу между ними. |
Дано: 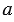
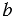

Найти: 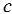


Решение:
1. По теореме косинусов: 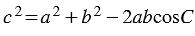

2. По теореме косинусов: 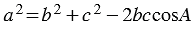

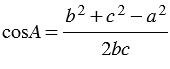
Задача 2
| Решение треугольника по стороне и прилежащим к ней углам. |
Дано: 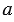


Найти: 
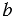
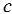
Решение:
2. По теореме синусов: 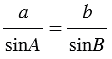
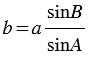
3. По теореме синусов: 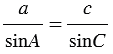

Задача 3
| Решение треугольника по трем сторонам. |
Дано: 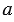
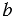
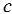
Найти: 


Решение:
1. По теореме косинусов: 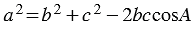

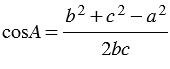
2. По теореме косинусов: 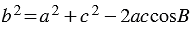
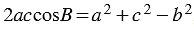
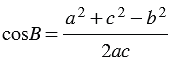
Пример
Стороны АВ, ВС и АС треугольника АВС соответственно равны 20 м, 14 м и 18 м. Определите значение угла А.
Решение:
По условию задачи 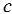
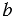
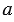
Следовательно, мы можем решить данный треугольник по трем сторонам (см. задачу 3), значит, найти угол А.
По теореме косинусов: 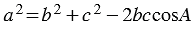

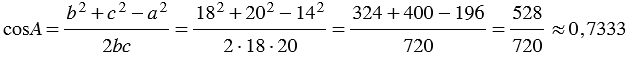
По таблице Брадиса находим угол А: 
Поделись с друзьями в социальных сетях: