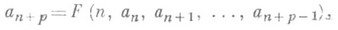Что значит рекуррентное соотношение
Рекуррентные соотношения и уравнения
В этом разделе вы найдете бесплатные примеры решений рекуррентных соотношений методом характеристического уравнения и подбора частного решения по правой части. Также приведены краткие алгоритмы решения для двух методов и пример их использования для последовательности Фибоначчи.
Как решать рекуррентные соотношения?
Для решения рекуррентных соотношений применяют один из двух основных способов:
В следующем разделе мы сравним, как выглядит процесс решения для одной и той же последовательности двумя методами.
Метод производящих функций
Метод характеристических функций
Этот метод практически полностью аналогичен методу решения линейных неоднородных дифференциальных уравнений с постоянными коэффициентами, кратко алгоритм выглядит так:
Решение для последовательности чисел Фибоначчи
Общая формула данной рекуррентной последовательности имеет вид6
Способ 1. Производящяя функция
$$\begin
Складываем все строчки:
На третьем шаге алгоритма приводим все суммы к замкнутому виду:
откуда выводим искомое выражение для производящей функции:
Теперь разложим ее в степенной ряд. Для этого сначала разложим знаменатель на множители. Найдем корни уравнения:
Чтобы разложить данные дроби в ряды, используем известное разложение для дроби:
Преобразуем данное выражение, используя то, что
Способ 2. Характеристическое уравнение
Тогда общее решение однородного рекуррентного уравнения имеет вид:
Решая систему, найдем
Итоговое выражение для последовательности чисел Фибоначчи:
Результаты обоих методов совпали, решение вторым методом оказалось проще и короче.
Примеры решений
Дискретная математика — рекуррентное соотношение
Определение
Рекуррентное отношение — это уравнение, которое рекурсивно определяет последовательность, в которой следующий член является функцией предыдущих членов (выражая F n как некоторую комбинацию F i с i n ).
Линейные рекуррентные отношения
Линейное рекуррентное уравнение степени k или порядка k — это рекуррентное уравнение в формате x n = A 1 x n − 1 + A 2 x n − 1 + A 3 x n − 1 + d o t s A k x n k ( A n — константа, а A k n e q 0 ) на последовательности чисел как полинома первой степени.
Вот некоторые примеры линейных рекуррентных уравнений —
| Рецидив отношений | Начальные значения | Решения |
|---|---|---|
| F n = F n-1 + F n-2 | a 1 = a 2 = 1 | Число Фибоначчи |
| F n = F n-1 + F n-2 | а 1 = 1, а 2 = 3 | Номер Лукаса |
| F n = F n-2 + F n-3 | a 1 = a 2 = a 3 = 1 | Падовская последовательность |
| F n = 2F n-1 + F n-2 | a 1 = 0, a 2 = 1 | Число Пелла |
Как решить линейное рекуррентное соотношение
Характеристическое уравнение для вышеуказанного рекуррентного соотношения —
Три случая могут возникнуть при поиске корней —
Характеристическое уравнение рекуррентного соотношения —
Итак, ( x − 3 ) ( x − 2 ) = 0
Корни реальны и различны. Итак, это в форме дела 1
F n = a x n 1 + b x n 2
Здесь F n = a 3 n + b 2 n ( A s x 1 = 3 a n d x 2 = 2 )
1 = F 0 = a 3 0 + b 2 0 = a + b
4 = F 1 = a 3 1 + b 2 1 = 3 a + 2 b
Решая эти два уравнения, мы получаем a = 2 и b = − 1
Следовательно, окончательное решение —
Характеристическое уравнение рекуррентного соотношения —
Следовательно, существует один действительный корень x 1 = 5
Поскольку существует единый действительный корень, он имеет вид случая 2
F n = a x n 1 + b n x n 1
Решая эти два уравнения, мы получаем a = 3 и b = 2 / 5
Характеристическое уравнение рекуррентного соотношения —
Термин « разностное уравнение» иногда (и для целей данной статьи) относится к определенному типу рекуррентного отношения. Однако «разностное уравнение» часто используется для обозначения любого рекуррентного отношения.
СОДЕРЖАНИЕ
Определение
Легко изменить определение для получения последовательностей, начиная с члена индекса 1 или выше.
Примеры
Факториал
Факториала определяется рекуррентным соотношением
и начальное условие
Логистическая карта
Примером рекуррентного отношения является логистическая карта :
с заданной постоянной r ; при начальном члене x 0 каждый последующий член определяется этим соотношением.
Числа Фибоначчи
Повторяемость второго порядка, которой удовлетворяют числа Фибоначчи, является каноническим примером однородного линейного рекуррентного отношения с постоянными коэффициентами (см. Ниже). Последовательность Фибоначчи определяется с использованием повторения
В явном виде рекуррентность приводит к уравнениям
Получаем последовательность чисел Фибоначчи, которая начинается
Биномиальные коэффициенты
Связь с разностными уравнениями в узком смысле
который можно упростить до
Собственно, нетрудно заметить, что
эквивалентно рекуррентному соотношению
Уравнения суммирования относятся к разностным уравнениям, как интегральные уравнения относятся к дифференциальным уравнениям.
От последовательностей к сеткам
Решение
Решение однородных линейных рекуррентных соотношений с постоянными коэффициентами
Корни характеристического многочлена
Те же коэффициенты дают характеристический многочлен (также «вспомогательный многочлен» или «сопутствующий многочлен»)
Для порядка 1 повторение
Решения таких рекуррентных соотношений более высокого порядка находятся систематическими средствами, часто с использованием того факта, что a n = r n является решением для рекуррентности именно тогда, когда t = r является корнем характеристического многочлена. К этому можно подойти напрямую или с помощью производящих функций ( формальных степенных рядов ) или матриц.
Рассмотрим, например, рекуррентное отношение вида
должно быть истинным для всех n > 1.
а если они идентичны (когда A 2 + 4 B = 0 ), мы имеем
Это наиболее общее решение; две константы C и D могут быть выбраны на основе двух заданных начальных условий a 0 и a 1 для получения конкретного решения.
можно переписать как
можно упростить решение, данное выше, как
Тогда неоднородную рекуррентность можно переписать в однородном виде как
который можно решить, как указано выше.
Условие устойчивости, сформулированное выше в терминах собственных значений для случая второго порядка, остается в силе для общего случая n- го порядка: уравнение является устойчивым тогда и только тогда, когда все собственные значения характеристического уравнения меньше единицы по модулю.
Для однородного линейного рекуррентного отношения с постоянными коэффициентами порядка d пусть p ( t ) будет характеристическим многочленом (также «вспомогательным многочленом»)
В результате этой теоремы однородное линейное рекуррентное соотношение с постоянными коэффициентами может быть решено следующим образом:
Это не совпадение. Рассматривая ряд Тейлора решения линейного дифференциального уравнения:
Эту эквивалентность можно использовать для быстрого решения рекуррентного соотношения для коэффициентов в решении степенного ряда линейного дифференциального уравнения.
Эмпирическое правило (для уравнений, в которых полином, умножающий первый член, не равен нулю в нуле):
и в более общем плане
Пример: рекуррентное соотношение для коэффициентов ряда Тейлора уравнения:
Этот пример показывает, как проблемы, обычно решаемые с использованием метода решения степенного ряда, преподаваемого в классах нормальных дифференциальных уравнений, могут быть решены намного проще.
Пример: дифференциальное уравнение
Преобразование дифференциального уравнения в разностное уравнение коэффициентов Тейлора имеет вид
Решение с помощью линейной алгебры
Линейно рекурсивная последовательность y порядка n
Решение для коэффициентов,
Это описание действительно не отличается от общего метода, приведенного выше, однако оно более лаконично. Это также хорошо работает в таких ситуациях, как
где есть несколько связанных повторений.
Решение с z-преобразованиями
Решение неоднородных линейных рекуррентных соотношений с постоянными коэффициентами
Это неоднородное повторение. Если мы подставим n ↦ n +1, мы получим рекуррентность
Вычитание исходной рекуррентности из этого уравнения дает
Это однородная повторяемость, которую можно решить описанными выше методами. В общем случае, если линейная рекурсия имеет вид
— производящая функция неоднородности, производящая функция
с постоянными коэффициентами c i получается из
Решение неоднородных рекуррентных соотношений первого порядка с переменными коэффициентами
Более того, для общего неоднородного линейного рекуррентного соотношения первого порядка с переменными коэффициентами:
есть также хороший способ решить эту проблему:
Решение общих однородных линейных рекуррентных соотношений
Решение рациональных разностных уравнений первого порядка
Стабильность
Устойчивость линейных возвратов высшего порядка.
Устойчивость линейных матричных повторений первого порядка
В матричном разностном уравнении первого порядка
Устойчивость нелинейных возвратов первого порядка.
Рассмотрим нелинейное возвращение первого порядка
Нелинейное рекуррентное соотношение может также иметь цикл периода k для k > 1. Такой цикл является устойчивым, что означает, что он привлекает набор начальных условий положительной меры, если составная функция
с появлением f k раз является локально устойчивым по тому же критерию:
Связь с дифференциальными уравнениями
При численном решении обыкновенного дифференциального уравнения обычно встречается рекуррентное соотношение. Например, при решении задачи начального значения
с помощью метода Эйлера и шага h вычисляются значения
Приложения
Биология
Информатика
Цифровая обработка сигналов
Например, уравнение для гребенчатого БИХ- фильтра с прямой связью с задержкой T следующее :
Экономика
РЕКУРРЕНТНОЕ СООТНОШЕНИЕ
рекуррентная формула,- соотношение вида
В случае, когда Р. с. линейно (см. Возвратная последовательность), задача описания множества всех последовательностей, удовлетворяющих данному Р. с., имеет аналогии с решением обыкновенного однородного линейного дифференциального уравнения с постоянными коэффициентами.
Лит.:[1] М а р к у ш е в и ч А. И., Возвратные последовательности, 2 изд., М., 1975. С. Н. Артемов.
Смотреть что такое «РЕКУРРЕНТНОЕ СООТНОШЕНИЕ» в других словарях:
рекуррентное соотношение — — [[http://www.rfcmd.ru/glossword/1.8/index.php?a=index d=23]] Тематики защита информации EN recurrence relation … Справочник технического переводчика
линейное рекуррентное соотношение — — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия EN linear recurrence … Справочник технического переводчика
Многочлены Эрмита — Многочлены Эрмита определённого вида последовательность многочленов одной вещественной переменной. Многочлены Эрмита возникают в теории вероятностей, в комбинаторике, физике. Эти многочлены названы в честь Шарля Эрмита. Содержание 1… … Википедия
Правильная скобочная последовательность — (ПСП) частный случай скобочной последовательности. Правильные скобочные последовательности образуют язык Дика и формально определяются следующим образом: (пустая строка) ПСП ПСП, взятая в скобки одного типа ПСП ПСП, к которой… … Википедия
Ортогональные многочлены — Пафнутий Львович Чебышёв В математике последовательностью ортогональных многочленов называют бесконечную последовательность действительных многочленов … Википедия
Фибоначчи — (Fibonacci) Фибоначчи первый крупный математик средневековой Европы Десятичная система счисления, арабские цифры, числа, последовательность, уровни, ряд, линии и спираль Фибоначчи Содержание >>>>>>>>> … Энциклопедия инвестора
ВАРИАЦИОННОЕ ИСЧИСЛЕНИЕ — численные методы раздел вычислительной математики, посвященный методам отыскания экстремальных значений функционалов. Численные методы В. и. принято разделять на два больших класса: непрямые и прямые методы. Непрямые методы основаны на… … Математическая энциклопедия
ВОЛЬТЕРРА УРАВНЕНИЕ — интегральное уравнение вида (линейное интегральное В. у. I рода) или вида (линейное интегральное В. у. II род а). Здесь х, s, a действительные числа, (вообще говоря) комплексный параметр, неизвестная функция, заданные функции, суммируемые с… … Математическая энциклопедия
Задача о порядке перемножения матриц — Задача о порядке перемножения матриц классическая задача динамического программирования, в которой дана последовательность матриц и требуется минимизировать количество скалярных операций для вычисления их произведения. Матрицы… … Википедия
Число Стирлинга первого рода — Числа Стирлинга первого рода количество перестановок из n предметов, имеющие ровно k циклов. Содержание 1 Определение 2 Рекуррентное соотношение 3 Пример 4 Свойст … Википедия
Решение рекуррентных соотношений
Содержание
Определения [ править ]
[math] F_0 = 0,\qquad F_1 = 1,\qquad F_
Для этого можно использовать метод производящих функций (англ. generating function method).
Метод производящих функций [ править ]
Примеры [ править ]
[math]1[/math] пример [ править ]
Производящие функции позволяют решать рекуррентные соотношение механически по одному и тому же алгоритму. Рассмотрим общую схему на простом примере, который позволит продемонстрировать базовые приёмы работы.
Задано линейное однородное рекуррентное соотношение порядка [math]2[/math] с постоянными коэффициентами:
[math]\begin
Будем искать производящую функцию последовательности в виде
[math] G(z)=\displaystyle\sum_
Теперь сложим все уравнения для всех значений [math]n[/math] :
[math] \underbrace
Аналогичные манипуляции со второй суммой дают нам выражение
[math] \displaystyle\sum_
откуда получаем производящую функцию последовательности в замкнутом виде:
[math] G(z) = \dfrac
Теперь разобьём дробь на сумму простых дробей:
[math] \dfrac
Из этого разложения следует, что
[math] \dfrac<1><1-3z>= \displaystyle\sum_
С другой стороны, мы искали [math]G(z)[/math] в виде
[math] G(z)=\displaystyle\sum_
поэтому, в силу равенства рядов, [math]a_n=3^n-2^n[/math] (для [math]n\geqslant 0[/math] ).
[math]2[/math] пример: числа Фибоначчи [ править ]
Рассмотрим рекуррентное соотношение для чисел Фибоначчи:
[math]\begin
Первый шаг алгоритма мы уже выполнили, записав рекуррентное соотношение. Выполним второй шаг:
[math]\begin
Складываем все строчки:
[math] f_0 + f_1 z + \displaystyle\sum_
Третий шаг алгоритма требует привести все суммы к замкнутому виду:
[math]\begin
откуда получаем замкнутое выражение для производящей функции:
[math] G(z) = \dfrac
Осталось разложить её в ряд (чего требует четвёртый шаг алгоритма). С этой целью нужно разложить знаменатель на множители. Найдем корни уравнения:
[math]\displaylines< 1-z-z^2 = 0 \cr z_1=-\dfrac<1-\sqrt<5>><2>, z_2=-\dfrac<1+\sqrt<5>><2>. > [/math]
Нам известно разложение следующей рациональной функции:
[math] \dfrac<1> <1-z>= \displaystyle\sum_
Рассмотрим первую дробь и поделим в ней числитель и знаменатель на [math]z_1[/math] :
[math] \dfrac
Аналогично (но с делением на [math]z_2[/math] ) поступим со второй дробью:
[math] \dfrac
[math]3[/math] пример [ править ]
Рекуррентное соотношение:
[math] \begin
[math]4[/math] пример [ править ]
Рассмотрим следующее рекуррентное соотношение:
[math]\begin
Вспомним, что
[math] (z^n)’ = nz^
поэтому
[math] \displaystyle\sum_
Последняя сумма может быть свёрнута:
[math] \displaystyle\sum_
Подставив свёрнутое выражение обратно, имеем,
[math] z\biggl(\displaystyle\sum_
Это уравнение для производящей функции. Из него выражаем [math]G(z)[/math] :
[math] G(z) = \dfrac<1-6z+11z^2-5z^3><(1-6z+8z^2)(1-z)^2>. [/math]
Дальше мы знаем что делать со всеми этими дробями, кроме, разве лишь, первой. Рассмотрим её (без множителя) подробнее:
[math] \dfrac<1> <(1-z)^2>=(1-z)^ <-2>=\displaystyle\sum_