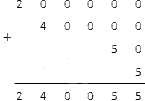Что значит разрядные слагаемые 5 класс
Сумма разрядных слагаемых натурального числа
Представленная статья посвящена интересной теме о натуральных числах. Для того, чтобы выполнять некоторые действия, необходимо представлять исходные выражения как сложение нескольких чисел – другим языком, раскладывать числа по разрядам. Обратный процесс также очень важен для решения упражнений и задач.
В данном разделе детально рассмотрим типичные примеры для лучшего усвоения информации. Мы также научимся преобразовывать натуральные числа и записывать их в другом виде.
Каким образом можно разложить число по разрядам?
Исходя из названия статьи, можно сделать вывод, что этот параграф посвящен таким математическим терминам, как «сумма» и «слагаемые». Перед тем, как приступить к изучению данной информации, следует подробно изучить тему, чтобы иметь понятие о натуральных числах.
Приступим к работе и рассмотрим основные понятия о разрядных слагаемых.
Следует помнить, что все разрядные слагаемые числа содержат разное количество знаков в своей записи.
Сумма разрядных слагаемых натурального числа равна этому числу.
Перейдем к понятию разрядных слагаемых.
Разрядные слагаемые– это такие натуральные числа, в записи которых содержится цифра, отличная от нуля. Количество чисел должно быть равно количеству цифр, не равных нулю. Все слагаемые числа могут записываться с различным количеством знаков. Если мы раскладываем число по разрядам, то сумма слагаемых числа всегда будет равна этому числу.
Проанализировав понятие, можно сделать вывод, что однозначные и многозначные числа (полностью состоящие из нулей за исключением первой цифры) нельзя представить в качестве суммы. Это происходит потому, что данные числа сами будут разрядными слагаемыми для каких-то чисел. За исключением данных чисел, все остальные примеры могут раскладываться на слагаемые.
Как раскладывать числа?
Смотря на этот пример, мы сможем любое натуральное число представить в виде суммы разрядных слагаемых.
Мы разобрали основные понятия. Разрядные слагаемые получили свое название из-за того, что каждое принадлежит к определенному разряду.
Как найти натуральное число, если известна сумма разрядных слагаемых?
Для того, чтобы разобрать данный пример, проанализируем обратную задачу. Представим, что нам известна сумма разрядных слагаемых. Нам необходимо найти данное натуральное число.
Еще один способ нахождения натурального числа – это сложение в столбцах разрядных слагаемых. Данный пример не должен вызвать у вас сложности во время выполнения. Поговорим об этом подробнее.
Осталось сложить числа по столбцам. Для этого нужно помнить, что сумма нулей равна нулю, а сумма нулей и натурального числа равна этому натуральному числу.
Получаем:
Поговорим еще об одном моменте. Если мы научимся раскладывать числа и представлять их в виде суммы разрядных слагаемых, то мы также сможем представлять натуральные число в виде суммы слагаемых, не являющихся разрядными.
Иногда сложные вычисления можно немного упростить. Рассмотрим еще небольшой пример для закрепления информации.
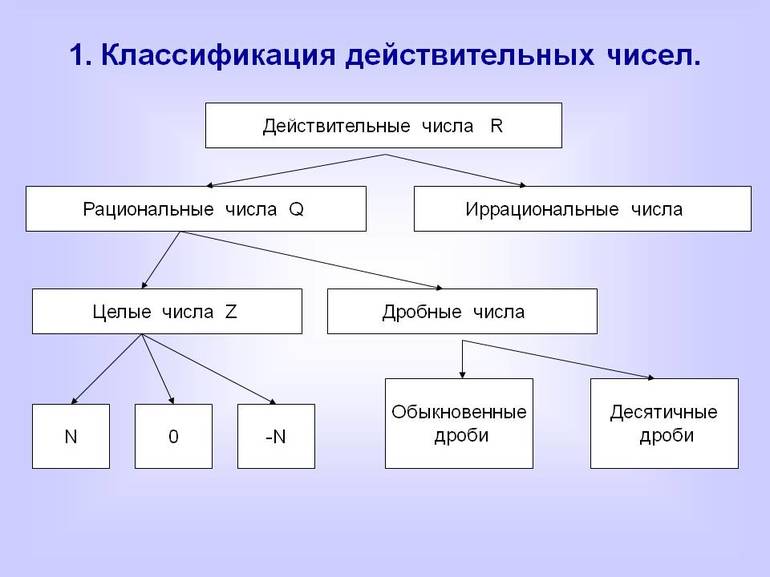
Натуральные числа и их классификация
Натуральными называют естественные величины, которые используются для счета (цифры и их комбинации: 1, 2, 3, 4, 5 и так далее), а также для расстановки по очереди (порядковые числительные: первый, второй, третий, четвертый и так далее). В совокупности они образуют так называемый ряд натуральных чисел. Его обозначением служит латинская буква N.
Главной особенностью этого ряда считается его бесконечность. Она обусловлена тем, что самого большого числа не существует. У любой составляющей ряда есть «старшие товарищи» — величины, которые по своему значению больше.
Распределение по категориям
Составляющие ряда натуральных чисел подразделяются на разряды и классы. Каждая из этих категорий неразрывно связана с другими. Разрядная классификация состоит из следующих групп (в скобках приведены слагаемые, соответствующие каждому разряду):
Разряд числа — это положение, которое оно занимает в цифровой записи. Таким образом, любое числовое значение можно представить посредством разрядных слагаемых по математической формуле следующего вида: nnnn = n000 + n00 + n0 + n, где n означает любую цифру от 0 до 9. Для наглядного примера стоит разбить на составляющие число 4698 = 4000 + 600 + 90 + 8. Получается, что оно состоит из четырех разрядов, отображенных соответствующими составляющими:
Разряд первого слагаемого называют высшим. Цифра, которой он обозначается, всегда больше нуля. Количество разрядов числа, как и количество его разрядных составляющих, всегда соответствует количеству в нем цифр, отличных от 0. Например, число 7052 состоит из трех разрядов, несмотря на свою четырехзначность. Это связано с тем, что в его составе отсутствуют сотни. Его слагаемые — семь тысяч, пять десятков и две простых единицы (7000 + 50 + 2 = 7052).
Разрядные составляющие — это натуральные числа, содержащие только одну цифру, отличную от нуля. Примеры разрядных слагаемых: 7, 30, 200, 4000 и тому подобные. Числа такого вида, как 12, 21, 475, 3500 и так далее, не могут быть отнесены к этой категории. Они подлежат математическому разложению на составляющие.
Название разрядных слагаемых обусловлено принадлежностью каждого из них к определенному разряду. Тысяча считается единицей четвертого разряда, сотня — единицей третьего разряда, десяток — второго, единица — первого. То есть нумерация разрядов начинается от наименьшей составляющей. Единицы первого разряда называются простыми, так как они однозначные. Составляющие прочих разрядов относятся к составным.
Каждый разряд состоит из десяти единиц, но обозначаться он может только девятью, так как десятая единица обеспечивает переход на следующий более высокий разряд. Не может быть разрядной составляющей типа десяти сотен — эта единица обозначается как одна тысяча.
Комплектация разрядов
В целях упрощения записи представления числа через разрядные составляющие единицы разрядов принято группировать в классы. В состав каждого из них входит три разряда:
Для удобства между классами разрешается ставить пробел. Особенно это необходимо для представлений очень больших величин (от миллиона), чтобы они не выглядели бесконечным набором цифр, и в процессе их разложения не возникло путаницы. На классы число разбивается строго по три цифры справа налево.
Первый класс — это единицы. Он включает от одного до трех разрядов. Это значит, что к нему относятся все натуральные числа от 1 до 999. Второй класс — это тысячи. В него входят от четырех до шести разрядов. То есть единицы, принадлежащие к этому классу, есть во всех величинах от 1000 и больше. Дальнейшее распределение по классам:
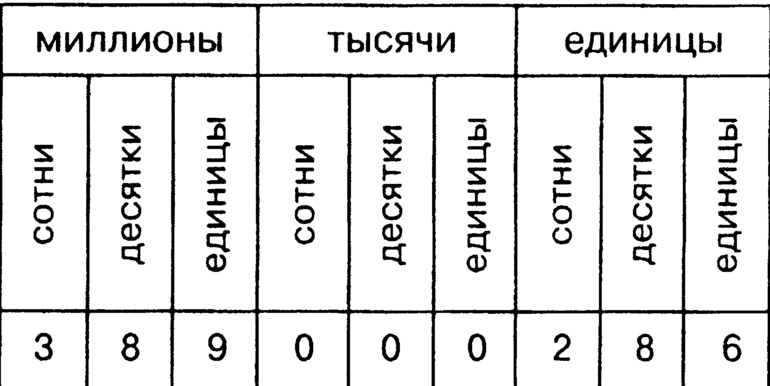
Распределение по классовым и разрядным категориям отображено в таблице:
Особенности разложения
Чтобы лучше понять, что такое разрядные слагаемые в математике и как их использовать, стоит подробно рассмотреть процесс разложения натуральных величин на эти составляющие. В основе большинства задач с разрядными слагаемыми лежит разложение натурального числа, то есть его представление в виде суммы разрядов через сложение количеств всех разрядных единиц.
Преобразить в сумму разрядных слагаемых можно каждую натуральную величину составного типа, то есть многозначную (двузначную, трехзначную и так далее). Чтобы разложить число на разрядные слагаемые корректно, необходимо соблюдать основные правила. Первое — нули не учитываются в разрядном составе числа. Второе — слагаемые записываются в порядке старшинства, то есть от старшего к младшему — вначале тысячи, затем сотни и десятки, последними фиксируются простые единицы.
Разрядный состав можно записать в трех вариантах разбора:
Вне зависимости от выбранного способа разложить число на составляющие по разрядам не составит особого труда. Конечно, чем больше число, тем выше риск запутаться и совершить ошибку. Упражняться лучше сперва на двузначных числах, а затем постепенно повышать разрядность.
Упражнения для тренировки
Для лучшего усвоения материала стоит разобрать несколько тренировочных упражнений. Несколько примеров, какими бывают математические задания по этой теме:
Нередки упражнения с обратным процессом, то есть такие, в которых нужно найти число по его составляющим:
Стоит отметить, что не все задачи с разрядными составляющими решаются путем сложения. Многие упражнения содержат прием их вычитания. Но сложными такие задания кажутся только на первый взгляд. Их суть проста. В скобках приводятся составляющие двух чисел — уменьшаемого и вычитаемого. Требуется найти их разность: (500 + 40 + 1) — (400 + 20) = (100 + 20 + 1) = 121.
Процессы разложения чисел по разрядам и обратного сложения имеют огромное значение для решения различных математических задач и упражнений. Очень важно уметь быстро раскладывать числа любой величины по разрядному составу. Это умение поможет в устном счете и оперировании многозначными числами.
Изучение натуральных чисел и разрядного состава входит в базовую программу по математике. Этот материал проходится учащимися в начальных классах школы.
Урок 11 Бесплатно Разложение числа по разрядам. Способы сложение натуральных чисел
Вы уже имеете общее представление об арифметической операции сложения и знаете свойства сложения натуральных чисел.
Сегодня вспомним наименования разрядов и классов.
Выясним, как записывают и читают большие натуральные числа.
Разберемся, что представляют собой разрядные слагаемые и как определить сумму разрядных слагаемых.
Познакомимся с различными способами и приемами сложения многозначных натуральных чисел, закрепим полученные знания на примерах.
Разряды и классы
С давних времен люди стремились не только уметь считать, но и уметь записывать числа.
Сначала для записи чисел применяли черточки, точки, метки и другие способы представления количества чего-либо, сейчас для этих целей используют цифры.
Сегодня цифры и числа окружают нас повсюду.
Мы не можем себе представить дату без чисел, невозможно измерить рост, массу, время, возраст, считать предметы, совершить покупку, продать, позвонить и т.д.
Число- это математическое понятие, которое используется для количественной характеристики, нумерации объектов и их частей, сравнения.
Каждое число состоит из цифр.
Цифрой называют знак, используемый для записи числа.
Цифры, которые мы используем в повседневной жизни, называют арабскими.
Их существует всего десять: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Все цифры кроме нуля называют значащими.
Нуль- это знак, который не указывает никакого числа, т.е. указывает на его отсутствие.
Запись числа с помощью десяти арабских цифр называют десятичной системой счисления.
Название системы счисления определяется ее основанием: количеством цифр, которые используются в данной системе счисления.
Цифры, из которых строятся числа десятичной системы счисления, называют узловыми:
1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Все остальные числа, которые состоят из узловых, называют алгоритмическими, например, 48, 35, 675, 2468 и т.д.
Десятичная система счисления является позиционной системой счисления, так как значение каждой цифры, из которых состоит число, зависит от ее позиции (места) в этом числе.
Место записи цифры в числе называют разрядом числа.
Счет разрядов идет справа налево.
В записи числа первая цифра справа называется цифрой первого разряда (разряд единиц)- это самый младший разряд.
Например, в числе 182 три разряда: первый разряд (разряд единиц) состоит из 2 единиц, второй разряд (разряд десятков) состоит из 8 десятков, третий разряд (разряд сотен) состоит из 1 сотни.
Если в записи числа вместо какого-либо разряда стоит «0» (нуль), то это означает, что цифра данного разряда отсутствует.
Сравним прочтение чисел 201 и 241
Каждые 10 единиц одного разряда составляют одну единицу следующего (более высокого разряда).
Например, единицы называют простыми единицами.
10 простых единиц составляют десяток.
10 десятков составляют сотню.
10 сотен составляют тысячу.
10 тысяч (один десяток тысяч) составляют десять тысяч (10000)
10 десятков тысяч составляют сто тысяч (100000)
Числа, которые записаны с помощью одной цифры, называют однозначными числами (числами первого порядка).
Числа, записанные с помощью двух цифр, называют двузначными числами (числами второго порядка).
Числа, которые состоят из трех цифр, называют трехзначными (числами третьего порядка) и т.д.
Пример:
1, 2, 5, 6— однозначные числа.
Самое маленькое однозначное натуральное число 1, самое большое- 9
10, 24, 38, 85— двузначные числа.
Самое маленькое двузначное натуральное число 10, самое большое- 99
278, 456, 882, 312— трехзначные числа.
Самое маленькое трехзначное натуральное число 100, самое большое- 999
Числа, для записи которых используют более одной цифры, называют многозначными числами.
Для удобства чтения многозначных чисел их разбивают на группы по три цифры, начиная справа; такие группы цифр называют классами.
Каждый класс содержит три разряда, записанных справа налево, начиная с разряда единиц, далее разряд десятков, затем идет разряд сотен.
Самый последний левый класс натурального многозначного числа может состоять из одного или двух разрядов.
Каждый класс имеет свое название.
Разряды повторяются по очереди в каждом классе, обозначая единицы, десятки и сотни соответствующих классов тысяч, миллионов, миллиардов и т.д.
Изобразим таблицу классов и разрядов натуральных чисел.
Таблица классов и разрядов чисел
У меня есть дополнительная информация к этой части урока!
Числа, которые имеют более 12 разрядов, т.е. числа от пятого класса и выше относятся к большим числам.
Числа, идущие после миллиарда названы в соответствии с латинскими наименованиями числительных.
Каждый последующий класс больших чисел содержит 1000 предыдущих.
1000 миллиардов = 1 триллион (представляет собой единицу и 12 нулей).
«Три» по латыни означает число «три».
1000 триллионов = 1 квадриллион (представляет собой единицу и 15 нулей)
«Квадра» по латыни означает число «четыре».
1000 квадриллионов = 1 квинтиллион (представляет собой единицу и 18 нулей)
«Квинта» по латыни- «пять» и т.д.
«Числа-гиганты» в повседневной жизни используют редко.
Применяются в основном в физике и астрономии для измерения массы и размеров звезд и планет, для расчета расстояний до различных небесных тел, расстояний между ними и т.д.
Удивительно, но большие числа можно отметить в человеческом теле.
Так, например, человеческий мозг состоит из 100 миллиардов нервных клеток- нейронов.
Посмотрим, как правильно читается большое число.
Чтобы прочитать многозначное натуральное число 184567483265, разобьем его на классы: Получим число вида: 184 567 483 265.
Прочитаем число, называя по очереди число единиц каждого класса слева направо.
При чтении класса единиц название данного класса, которым заканчивается любое натуральное число, не произносится.
184 миллиарда 567 миллионов 483 тысячи 265.
Не произносится также название класса, все три цифры которого нули.
Например, число 149500000 километров (число равное расстоянию от Земли до Солнца) прочитаем так: 149 миллионов 500 тысяч километров.
Пройти тест и получить оценку можно после входа или регистрации
Способы сложения натуральных чисел
Вы уже имеете общее представление об операции сложения чисел и знаете свойства сложения натуральных чисел.
Уроком ранее мы выяснили, что сложение- это арифметическая операция объединения исчисляемых объектов в одно целое.
Результат сложения чисел называют суммой этих чисел.
Складываемые числа называют слагаемыми.
Для записи сложения используют знак плюс «+»
В повседневной жизни, на работе, на учебе возникает необходимость оперативно и качественно решать задачи и производить определенные арифметические действия, выбирая для этого оптимально удобный способ решения.
Сейчас рассмотрим некоторые способы и приемы, позволяющие верно, быстро и легко вычислит сумму натуральных чисел.
1. Таблица сложения натуральных чисел
Для сложения чисел первого десятка удобно пользоваться таблицей сложения, с которой вы знакомились в начальных классах.
Запомнив данную таблицу наизусть, легко и просто выполнить задание на вычисление суммы чисел.
Разберем правила пользования таблицей сложения натуральных чисел.
Известно, что операция сложения выглядит так:
Слагаемое №1 + Слагаемое №2 = Сумма
Таблица представляет собой квадрат, разбитый на десять строк и десять столбцов.
По верхнему краю и по левому краю пронумерованы ячейки от 1 до 10
У меня есть дополнительная информация к этой части урока!
Алгоритм сложения двух натуральных чисел с помощью таблицы:
1. В самой верхней строке необходимо выбрать из десяти ячеек ту, в которой содержится значение первого слагаемого.
2. Выбрать в самом левом столбце ячейку, в которой находится значение второго слагаемого.
3. Суммой будет являться число, расположенное в ячейке, образованной пересечением соответствующих столбца и строки в поле таблицы.
Например, чтобы сложить два натуральных числа 4 и 7, нужно выполнить следующие действия:
Таким образом, 4 + 7 = 11
Такой же результат будет получен, если с помощью таблицы сложим 7 и 4.
Таким образом, 7 + 4 = 11
Таблицей удобно пользоваться при сложении многозначных чисел по разрядам, если условно принять, что в таблице складываются десятки с десятками или сотни с сотнями, или тысячи с тысячами и т.д.
Пример:
Найдите сумму чисел 20 и 60 с помощью таблицы сложения натуральных чисел.
С помощью таблицы уже известным способом сложим числа 2 и 6, суммой данных чисел является ячейка со значением 8.
Условно представим, что ячейка со значением 2— это 2 десятка, ячейка со значением 6— это 6 десятков.
Следовательно, ячейка с результатом 8, образованная пересечением соответствующего столбца и строки, по смыслу означает 8 десятков.
20 + 60 = 80
Ответ: 80
Для перехода при сложении на следующий разряд вспомним, что каждые 10 единиц одного разряда составляют одну единицу следующего (более высокого разряда).
Пример:
Вычислите по таблице сумму чисел 700 и 300.
С помощью таблицы уже известным способом сложим числа 7 и 3, суммой данных чисел является ячейка со значением 10
Условно представим, что ячейка со значением 7— это 7 сотен, ячейка со значением 3 означает 3 сотни.
Следовательно, ячейка с результатом 10, образованная пересечением соответствующего столбца и строки, по смыслу означает 10 сотен.
Нам известно, что 10 сотен = 1000
Таким образом, получаем 700 + 300 = 1000
Ответ: 1000
Пример:
Вычислите сумму 60 и 70 с помощью таблицы сложения.
По таблице сложения чисел видно, что 6 + 7 = 13
Следовательно, если сложить 6 десятков и 7 десятков, получим 13 десятков.
Так как число 13 состоит из 1 десятка и 3 единиц, то 13 десятков состоят из 10 десятков и 3 десятков.
10 десятков = 100
3 десятка = 30
Получим 100 + 30 = 130.
Ответ: 130
Конечно, таблица сложения натуральных чисел позволяет наглядно легко и быстро определить сумму чисел, но не всегда она находится под рукой.
2. Способ поразрядного сложения натуральных чисел.
Рассмотрим еще один способ определения суммы чисел.
Первым делом научимся представлять натуральные числа в виде суммы разрядных слагаемых.
Разрядные слагаемые натурального числа имеют ряд характерных признаков:
1. Разрядные слагаемые- это числа, в записи которых находится только одна цифра, отличная от нуля.
Например, 10, 200, 6000, 40000 и т.д.
2. Разрядные слагаемые одного натурального числа имеют разное количество знаков в своей записи (т.е. состоят из разного количества цифр).
3. Количество разрядных слагаемых натурального числа должно быть равно количеству цифр, отличных от нуля, в записи числа.
Сумма разрядных слагаемых— это запись многозначного числа, как суммы его разрядных единиц.
Сумма разрядных слагаемых равна исходному натуральному числу.
Любое натуральное число можно записать в виде суммы разрядных слагаемых.
Для этого необходимо:
1. Определить по количеству цифр в числе количество разрядных слагаемых, отличных от нуля.
2. Определить количество единиц, десятков, сотен, тысяч и т.д.
3. Записать число в виде суммы разрядных слагаемых.
Пример:
Разложите натуральное число 2456 в виде суммы разрядных слагаемых.
Число 2456 представляет собой сумму четырех разрядных слагаемых (так как число состоит из 4 цифр, неравных нулю).
Число 2456 содержит:
2456 = 2 тысячи + 4 сотни + 5 десятков + 6 единиц = 2000 + 400 + 50 + 6
Рассмотрим алгоритм поразрядного сложения натуральных чисел.
1. Слагаемые разложить на разрядные слагаемые.
2. Выполнить сложение одноименных разрядов (единиц с единицами, десятки с десятками и т.д.) используя при этом переместительное и сочетательное свойства сложения.
Пример:
Найдите сумму чисел 245 и 25 способом последовательного поразрядного сложения.
Разложим первое и второе слагаемое на разрядные слагаемые.
245 = 2 сотни + 4 десятка + 5 единиц = 200 + 40 + 5
25 = 2 десятка + 5 единиц = 20 + 5
Выполним сложение одноименных разрядов чисел 245 и 25.
245 + 25 = 200 + 40 + 5 + 20 + 5 = 200 + (40 + 20) + (5 + 5) = 200 + (60 + 10) = 200 + 70 = 270
Получаем 245 + 25 = 270
Ответ: 270
3. Сложение натуральных чисел «столбиком»
Рассмотренный способ поразрядного сложения довольно громоздкий в оформлении и не очень удобный для определения суммы больших чисел или нескольких больших чисел.
Поэтому часто многозначные числа складывают в столбик.
Чтобы сложить натуральные числа данным способом, нужно записать слагаемые в столбик так, чтобы цифры одноименных разрядов находились друг под другом (единицы под единицами, десятки под десятками, сотни под сотнями и т.д.).
При сложении столбиком самая правая цифра одного числа (разряд единиц первого слагаемого) должна располагаться под самой правой цифрой другого числа (разряд единиц второго слагаемого).
Нам известно, что от перестановки слагаемых сумма не меняется, следовательно, записывать слагаемые в столбик можно в любом порядке.
Затем слева между числами-слагаемыми ставится знак плюс «+».
Под нижним слагаемым проводится горизонтальная черта.
Сложение чисел начинается с разряда единиц (с крайнего правого столбца).
Складывают цифры одного разряда, результат записывают под горизонтальной чертой под тем разрядом, в котором выполнялось сложение.
Если в результате получается число меньше 10 (однозначное число), то оно записывается в столбик соответствующего разряда под чертой.
Если в результате получается двузначное число, то под чертой записывается значение разряда единиц полученного числа, а число десятков либо запоминается (держится в уме), либо подписывается сверху над следующим столбиком в дополнительной строке.
Далее складываются числа в следующем столбике, т.е. складываются значение следующего разряда слагаемых.
Действия совершаются аналогично изложенным выше, однако к суме еще добавляется число десятков, которые «держали в уме» (если такое было).
Соответственно, если получается однозначное число, его записывают под чертой в столбик соответствующего разряда.
Если число в результате сложения получается двузначное, то снова под линией записывается число единиц полученного промежуточного значения, а значение десятков запоминается или записывается в дополнительной строке.
Так происходит переход к следующему столбику (следующим разрядам слагаемых) и производятся все выше описанные действия.
Натуральное число, которое образуется после завершения операции сложения, является результатом суммы исходных чисел.
Пример:
Выполните сложение двух чисел 75806 и 2798.
Запишем два числа в столбик так, чтобы одноименные разряды стояли друг под другом.
Между числами поставим знак плюс «+», под нижним слагаемым проведем горизонтальную черту.
Складываем числа из правого столбца: 6 и 8.
Получаем число 14— двузначное число.
Под горизонтальной линией записываем число 4 (значение разряда единиц числа 14), а число 1 (значение разряда десятков числа 14) запоминаем.
Записываем запомненную 1 сверху в дополнительной строке над соседним столбцом.
Продолжаем вычисление, складываем цифры слагаемых, стоящих во втором столбце справа.
Так как 0 + 0 = 0, но была запомнена 1, то получим 0 + 0 + 1 = 1
Число 1— однозначное число, следовательно, его просто записываем под чертой в соответствующем разряде.
Переходим к следующему столбцу.
Складываем 8 и 9, при этом в памяти нет никаких запомненных чисел, поэтому больше ничего к ним не прибавляем
8 + 9 = 17
Получили двузначное число 17.
Следовательно, число 7 записываем под горизонтальной чертой (значение разряда единиц числа 17), а число 1 (значение разряда десятков числа 17) запоминаем.
Записываем запомненную 1 сверху в дополнительной строке над соседним столбцом.
Переходим к четвертому столбцу.
Складываем 5 и 7.
В памяти была запомнена 1, поэтому к сумме чисел 5 и 7 прибавляем 1.
5 + 7 + 1 = 13
Получили двузначное число 13.
Следовательно, число 3 записываем под горизонтальной чертой, а число 1 запоминаем, переносим в следующий разряд.
На последнем шаге складываем 2 и 7
2 + 7 = 9
К 9 прибавляем запомненную 1, получаем: 9 + 1 = 10
Но в следующем столбце исходные слагаемые не имеют цифр, запомненную 1 сносим вниз и записываем под чертой.
Сложение двух натуральных чисел 75806 и 27908 завершено, сумма данных чисел равна 103714
75806 + 27908 = 103714
Ответ: 103714
Столбиком можно складывать различное количество слагаемых.
Алгоритм выполнения операции сложения в столбик нескольких слагаемых будет абсолютно аналогичным.
4. Группировка слагаемых и округление натуральных чисел.
Данный способ сложения натуральных чисел кратко уже был рассмотрен на прошлом уроке.
Известно, что число, которое оканчивается на нуль или несколько нулей, называют круглым числом.
С круглыми числами легко совершать арифметические операции.
Сложение способом округления натуральных чисел применяют, когда из слагаемых можно выбрать такие, которые в сумме будут давать круглые числа.
Разность между круглым и исходным числом называется арифметическим дополнением.
Чтобы произвести сложение многозначных натуральных чисел способом округления, необходимо:
1. Одно из слагаемых, которое близко к круглому числу, округлить.
2. Выполнить операцию сложения.
3. Из полученной суммы вычесть арифметическое дополнение.
Пример:
Найдите сумму чисел 1448 и 298
Округлим число 298 до 300, а затем вычтем из полученной суммы арифметическое дополнение, равное 2
Получим выражение вида:
Ответ: 1746
Совместно с данным способом сложения натуральных чисел используют группировку слагаемых и применяют основные свойства сложения.
При вычислении суммы, состоящей из трех и более слагаемых, удобно использовать переместительное и сочетательное свойство сложения, группируя слагаемые, объединяя их по определенному признаку с помощью скобок таким образом, чтобы в сумме они давали круглые числа.
Пример:
Найдите сумму чисел 46 + 28 + 134 + 61
Группируем числа так, чтобы в результате сложения этих чисел получалось круглое число.
Используя переместительное и сочетательное свойство сложения, переставим местами слагаемые и сгруппируем их.
46 + 28 + 134 + 61 = (46 + 134) + (28 + 61) = 180 + 89
Округлим число 89 до 90
В связи с этим из суммы чисел 180 и 90 вычтем арифметическое дополнение, равное 1
Ответ: 269
Пройти тест и получить оценку можно после входа или регистрации