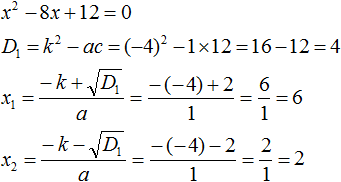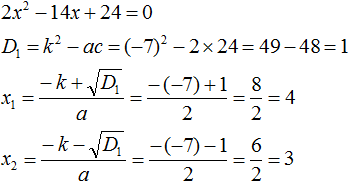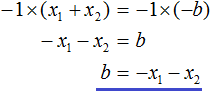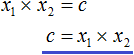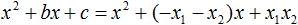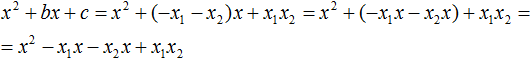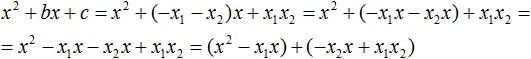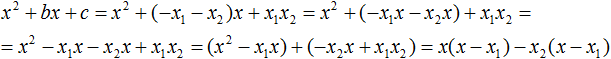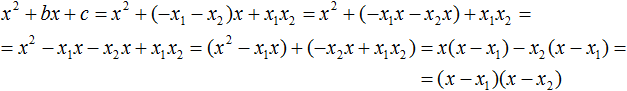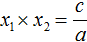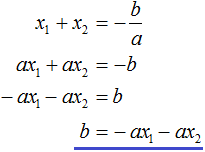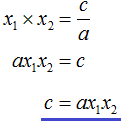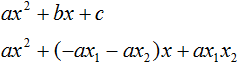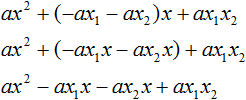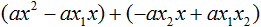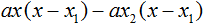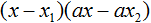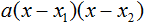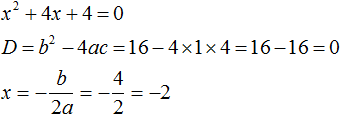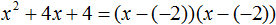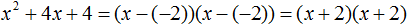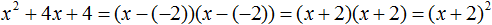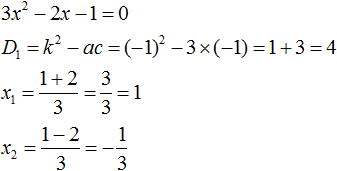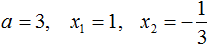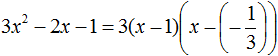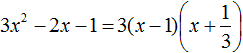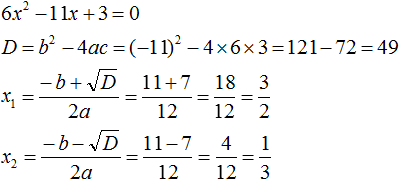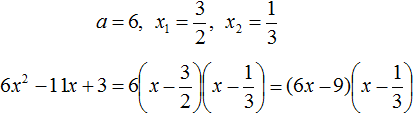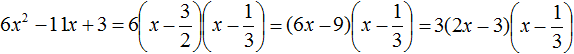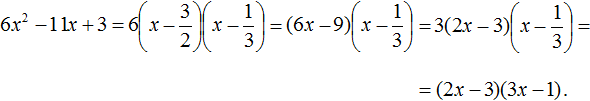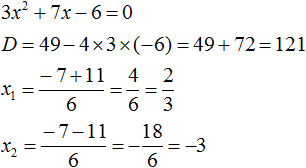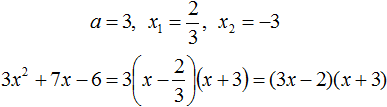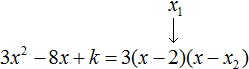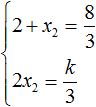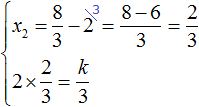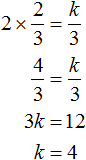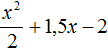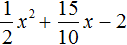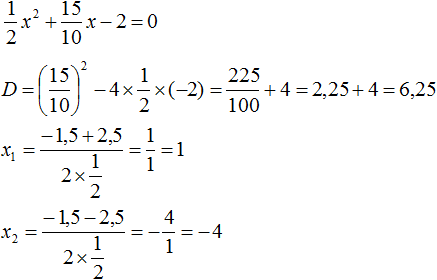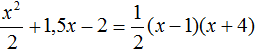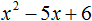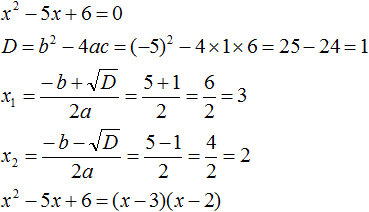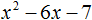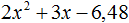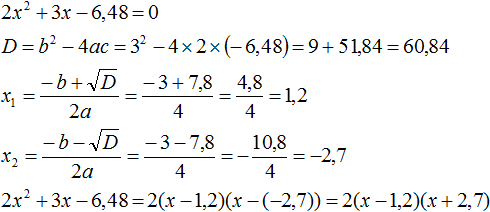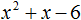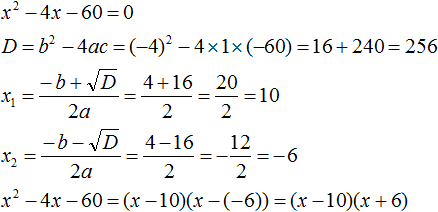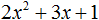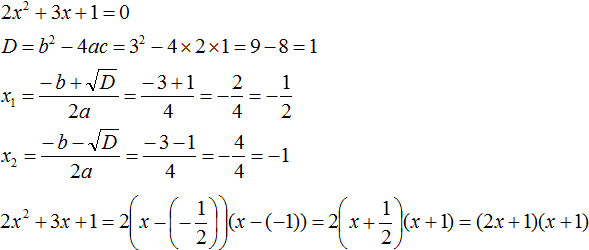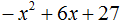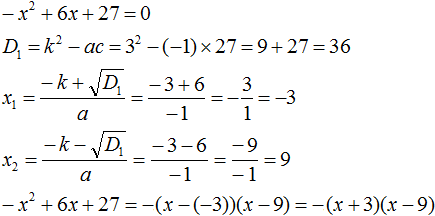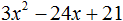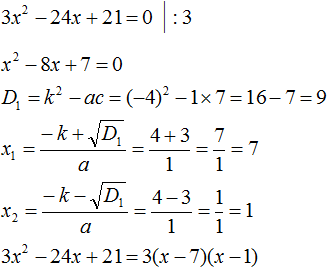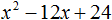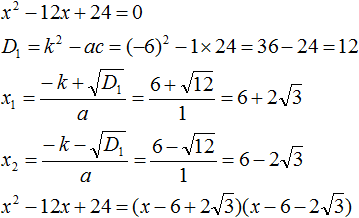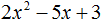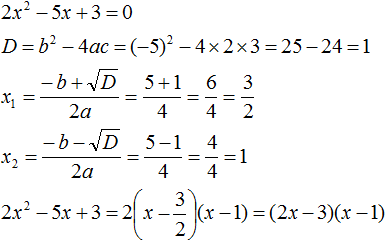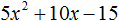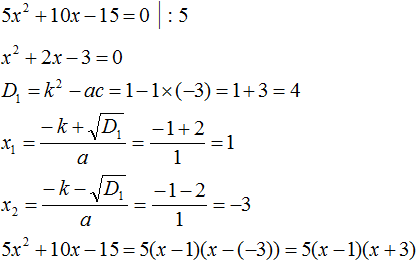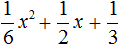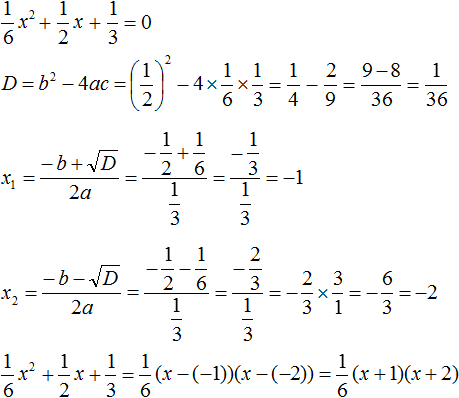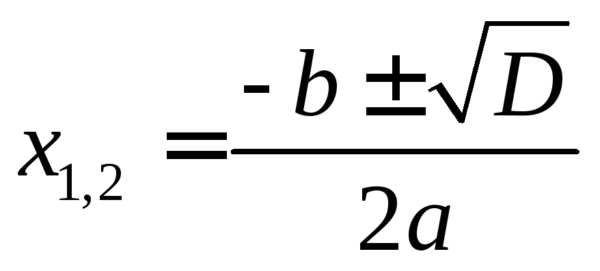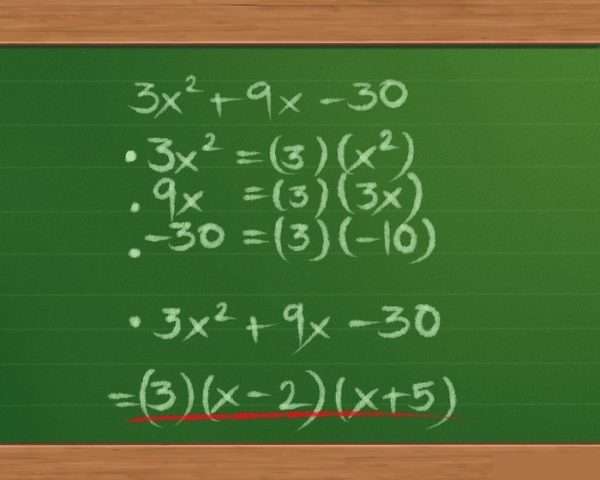Что значит разложить на множители квадратный трехчлен
Квадратный трехчлен. Разложение квадратного трехчлена на множители
Квадратный трехчлен – это многочлен вида \(ax^2+bx+c\) (\(a≠0\)).
Примеры не квадратных трехчленов:
Корень квадратного трехчлена:
Значение переменной \(x\), при котором квадратный трехчлен обращается в ноль, называют его корнем.
Пример:
У трехчлена \(x^2-2x+1\) корень \(1\), потому что \(1^2-2·1+1=0\)
У трехчлена \(x^2+2x-3\) корни \(1\) и \(-3\), потому что \(1^2+2-3=0\) и \((-3)^2-6-3=9-9=0\)
Чтобы найти корни квадратного трехчлена нужно решить соответствующее квадратное уравнение.
Например: если нужно найти корни для квадратного трехчлена \(x^2-2x+1\), приравняем его к нулю и решим уравнение \(x^2-2x+1=0\).
Готово. Корень равен \(1\).
Разложение квадратного трёхчлена на множители:
Квадратный трехчлен \(ax^2+bx+c\) можно представить как \(a(x-x_1)^2\), если дискриминант уравнения \(ax^2+bx+c=0\) равен нулю.
Квадратный трехчлен \(ax^2+bx+c\) не раскладывается на множители, если дискриминант уравнения \(ax^2+bx+c=0\) меньше нуля.
Например, у трехчленов \(x^2+x+4\) и \(-5x^2+2x-1\) – дискриминант меньше нуля. Поэтому разложить их на множители невозможно.
Пример. Разложите на множители \(2x^2-11x+12\).
Решение:
Найдем корни квадратного уравнения \(2x^2-11x+12=0\)
Полученный ответ, может быть, записать по-другому: \((2x-3)(x-4)\).
Пример. (Задание из ОГЭ) Квадратный трехчлен разложен на множители \(5x^2+33x+40=5(x++ 5)(x-a)\). Найдите \(a\).
Решение:
\(5x^2+33x+40=0\)
\(D=33^2-4 \cdot 5 \cdot 40=1089-800=289=17^2\)
\(x_1=\frac<-33-17><10>=-5\)
\(x_2=\frac<-33+17><10>=-1,6\)
\(5x^2+33x+40=5(x+5)(x+1,6)\)
Ответ: \(-1,6\)
Разложение квадратного трёхчлена на множители
Как разложить на множители квадратный трёхчлен
В прошлых уроках мы решали квадратные уравнения. Общий вид таких уравнений выглядел так:
Левая часть этого уравнения является квадратным трёхчленом.
Одним из полезных преобразований при решении задач является разложение квадратного трёхчлена на множители. Для этого исходный квадратный трёхчлен приравнивают к нулю и решают квадратное уравнение. В этом случае говорят, что выполняется поиск корней квадратного трёхчлена.
Полученные корни x1 и x2 следует подстáвить в следующее выражение, которое и станет разложением:
Таким образом, чтобы разложить квадратный трёхчлен на множители при помощи решения квадратного уравнения, нужно воспользоваться следующей готовой формулой:
Где левая часть — исходный квадратный трёхчлен.
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена. Для этого приравняем данный квадратный трёхчлен к нулю и решим квадратное уравнение:
В данном случае коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента. Чтобы сэкономить время, некоторые подробные вычисления можно пропустить:
Если a равно единице (как в данном примере), то решение можно записать покороче:
Чтобы проверить правильно ли разложен квадратный трёхчлен на множители, нужно раскрыть скобки у правой части получившегося равенства.
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Приравняем данный квадратный трёхчлен к нулю и решим уравнение:
Как и в прошлом примере коэффициент b является чётным. Поэтому можно воспользоваться формулами для чётного второго коэффициента:
Выполним проверку. Для этого раскроем скобки у правой части получившегося равенства. Если мы всё сделали правильно, то должен получиться квадратный трёхчлен 2x 2 − 14x + 24
Как это работает
Разложение квадратного трёхчлена на множители происходит, если вместо коэффициентов квадратного трёхчлена подстáвить теорему Виета и выполнить тождественные преобразования.
Для начала рассмотрим случай, когда коэффициент a квадратного трёхчлена равен единице:
Вспоминаем, что если квадратное уравнение является приведённым, то теорема Виета имеет вид:
Переменную c из теоремы Виета выражать не нужно — она уже выражена. Достаточно поменять местами левую и правую часть:
Теперь подставим выраженные переменные b и c в квадратный трёхчлен x 2 + bx + c
Раскроем скобки там где это можно:
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Далее замечаем, что выражение ( x − x1 ) является общим множителем. Вынесем его за скобки:
Но это был случай, когда исходный квадратный трёхчлен является приведённым. В нём коэффициент a равен единице. И соответственно, в формуле разложения такого квадратного трехчлена коэффициент a можно опустить.
Теперь рассмотрим случай, когда коэффициент a квадратного трёхчлена не равен единице. Это как раз тот случай, когда в формуле разложения присутствует перед скобками коэффициент a
Это потому что теорема Виета работает только для приведённых квадратных уравнений. А чтобы уравнение ax 2 + bx + c = 0 стало приведённым, нужно разделить обе его части на a
Далее чтобы квадратный трёхчлен вида ax 2 + bx + c разложить на множители, нужно вместо b и c подставить соответствующие выражения из теоремы Виета. Но в этот раз нам следует использовать равенства 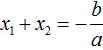
В получившемся выражении выполним разложение многочлена на множители способом группировки. В данном случае удобно сгруппировать первый член со вторым, а третий с четвёртым:
Далее замечаем, что выражение x − x1 тоже является общим множителем. Вынесем его за скобки:
Скобки внутри скобок можно раскрыть. Тогда получим следующее:
При этом если нужно получить короткий ответ, последнее выражение можно записать в виде (x + 2) 2 поскольку выражение (x + 2)(x + 2) это перемножение двух сомножителей, каждый из которых равен (x + 2)
Примеры разложений
Пример 1. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Во вторых скобках можно заменить вычитание сложением:
Пример 2. Разложить на множители следующий квадратный трёхчлен:
Упорядочим члены так, чтобы старший коэффициент располагался первым, средний — вторым, свободный член — третьим:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Упростим получившееся разложение. Вынесем за первые скобки общий множитель 3
Теперь воспользуемся сочетательным законом умножения. Напомним, что он позволяет перемножать сомножители в любом порядке. Умножим 3 на вторые скобки. Это позвóлит избавиться от дроби в этих скобках:
Пример 3. Разложить на множители следующий квадратный трёхчлен:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
В данном случае квадратный трёхчлен не является приведённым, поэтому сумма его корней будет равна дроби 
Выразим из первого равенства переменную x2 и сразу подстáвим найденное значение во второе равенство вместо x2
Пример 5. Разложить на множители следующий квадратный трёхчлен:
Перепишем данный трёхчлен в удобный для нас вид. Если в первом члене заменить деление умножением, то получим 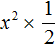
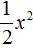
Коэффициент b можно перевести в обыкновенную дробь. Так проще будет искать дискриминант:
Найдём корни квадратного трёхчлена:
Воспользуемся формулой разложения:
Задания для самостоятельного решения
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Как разложить на множители квадратный трехчлен: формула
Разложение многочленов для получения произведения иногда кажется запутанным. Но это не так сложно, если разобраться в процессе пошагово. В статье подробно рассказано, как разложить на множители квадратный трехчлен.
Понятие и определение
Многим непонятно, как разложить на множители квадратный трехчлен, и для чего это делается. Сначала может показаться, что это бесполезное занятие. Но в математике ничего не делается просто так. Преобразование нужно для упрощения выражения и удобства вычисления.
Многочлен, имеющий вид – ax²+bx+c, называется квадратным трехчленом. Слагаемое «a» должно быть отрицательным или положительным. На практике это выражение называется квадратным уравнением. Поэтому иногда говорят и по-другому: как разложить квадратное уравнение.
Интересно! Квадратным многочлен называют из-за самой его большой степени – квадрата. А трехчленом из-за 3-х составных слагаемых.
Некоторые другие виды многочленов:
Разложение квадратного трехчлена на множители
Сначала выражение приравнивается к нулю, затем нужно найти значения корней x1 и x2. Корней может не быть, может быть один или два корня. Наличие корней определяется по дискриминанту. Его формулу надо знать наизусть: D=b²-4ac.
Если результат D получается отрицательный, корней нет. Если положительный – корня два. Если в результате получился ноль – корень один. Корни тоже высчитываются по формуле.
Формулы для разных значений дискриминанта различаются.
Если D положительный:
Если выражение отрицательное, считать ничего не нужно.
Это интересно! Как найти и чему будет равна длина окружности
Онлайн калькуляторы
В интернете есть онлайн калькулятор. С его помощью можно выполнить разложение на множители. На некоторых ресурсах предоставляется возможность посмотреть решение пошагово. Такие сервисы помогают лучше понять тему, но нужно постараться хорошо вникнуть.
Если тема понятна, рекомендуется использовать онлайн калькулятор для проверки решения.
Полезное видео: Разложение квадратного трехчлена на множители
Примеры
Предлагаем просмотреть простые примеры, как разложить квадратное уравнение на множители.
Пример 1
Здесь наглядно показано, что в результате получится два x, потому что D положительный. Их и нужно подставить в формулу. Если корни получились отрицательные, знак в формуле меняется на противоположный.
Нам известна формула разложения квадратного трехчлена на множители: a(x-x1)(x-x2). Ставим значения в скобки: (x+3)(x+2/3). Перед слагаемым в степени нет числа. Это значит, что там единица, она опускается.
Это интересно! Как раскрыть модуль действительного числа и что это такое
Пример 2
Этот пример наглядно показывает, как решать уравнение, имеющее один корень.
Подставляем получившееся значение:
Пример 3
Сначала вычислим дискриминант, как в предыдущих случаях.
Дискриминант отрицательный, значит, корней нет.
После получения результата стоит раскрыть скобки и проверить результат. Должен появиться исходный трехчлен.
Альтернативный способ решения
Некоторые люди так и не смогли подружиться с дискриминантом. Можно еще одним способом произвести разложение квадратного трехчлена на множители. Для удобства способ показан на примере.
Это интересно! Уроки математики: умножение на ноль главное правило
Далее выполняем подбор и смотрим, чтобы получилось выражение, которое было сначала:
Значит, преобразование выражения x2+3x-10 выглядит так: (x-2)(x+5).
Важно! Стоит внимательно следить за тем, чтобы не перепутать знаки.
Разложение сложного трехчлена
Если «a» больше единицы, начинаются сложности. Но все не так трудно, как кажется.
Чтобы выполнить разложение на множители, нужно сначала посмотреть, возможно ли что-нибудь вынести за скобку.
Например, дано выражение: 3x²+9x-30. Здесь выносится за скобку число 3:
3(x²+3x-10). В результате получается уже известный трехчлен. Ответ выглядит так: 3(x-2)(x+5)
Схема мало отличается от предыдущей. Есть лишь несколько новых моментов. Допустим, дано выражение: 2x²+7x+3. Ответ также записывается в 2-х скобках, которые нужно заполнить (_)(_). Во 2-ю скобку записывается x, а в 1-ю то, что осталось. Это выглядит так: (2x_)(x_). В остальном повторяется предыдущая схема.
Число 3 дают числа:
Решаем уравнения, подставляя данные числа. Подходит последний вариант. Значит, преобразование выражения 2x²+7x+3 выглядит так: (2x+1)(x+3).
Это интересно! Считаем правильно: как находить процент от суммы и числа
Другие случаи
Преобразовать выражение получится не всегда. При втором способе решение уравнения не потребуется. Но возможность преобразования слагаемых в произведение проверяется только через дискриминант.
Стоит потренироваться решать квадратные уравнения, чтобы при использовании формул не возникало трудностей.
Полезное видео: разложение трехчлена на множители
Вывод
Пользоваться можно любым способом. Но лучше оба отработать до автоматизма. Также научиться хорошо решать квадратные уравнения и раскладывать многочлены на множители нужно тем, кто собирается связать свою жизнь с математикой. На этом строятся все следующие математические темы.