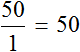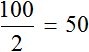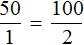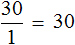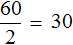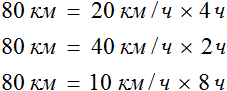Что значит разделить пропорционально числам

Пропорциональное деление

Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.

Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.

Деление числа на пропорциональные части

Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.

Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:

Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:

Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.

90 : (1 + 2 + 3) = 90 : 6 = 15;

Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.

Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.

Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:

значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то

Второй способ: обозначим искомые части буквами a, b и c:

Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:

Следовательно, c равно:

Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:

так как 15 + 10 + 8 = 33, то

Деление на части, обратно пропорциональные числам

Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как

Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:

Источник

Прямая и обратная пропорциональность

Основные определения

Математическая зависимость — это соответствие между элементами двух множеств, при котором каждому элементу одного множества ставится в соответствие элемент из другого множества.

Пропорция в математике — это равенство между отношениями двух или нескольких пар чисел или величин. Пропорциональными называются две взаимно-зависимые величины, если отношение их значений остается неизменным.

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз. Проще говоря — это зависимость одного числа от другого.

Есть две разновидности пропорциональностей:

Коэффициент пропорциональности — это неизменное отношение пропорциональных величин. Он показывает, сколько единиц одной величины приходится на единицу другой. Коэффициент пропорциональности обозначается латинской буквой k.

Прямо пропорциональные величины

Две величины называются прямо пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая увеличивается (или уменьшается) во столько же раз.

Прямая пропорциональность в виде схемы: «больше — больше» или «меньше — меньше».

a и d называются крайними членами, b и c — средними.

Свойство прямо пропорциональной зависимости:

Если две величины прямо пропорциональны, то отношения соответствующих значений этих величин равны.

Примеры прямо пропорциональной зависимости:

Если говорить метафорами, то прямую пропорциональную зависимость можно отличить от обратной по пословице: «Чем дальше в лес, тем больше дров». Что значит, чем дольше ты идешь по лесу, тем больше дров можно собрать.

Формула прямой пропорциональности

y = kx,

где y и x — переменные величины, k — постоянная величина, которую называют коэффициентом прямой пропорциональности.

Коэффициент прямой пропорциональности — это отношение любых соответствующих значений пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента прямой пропорциональности:

Пример 1.

В одно и то же путешествие поехали два автомобиля. Один двигался со скоростью 70 км/ч и за 2 часа проделал тот же путь, что другой за 7 часов. Найти скорость второго автомобиля.

Пример 2.

Блогер за 8 дней может написать 14 постов. Сколько помощников ему понадобится, чтобы написать 420 постов за 12 дней?

Количество человек (блогер и помощники) увеличивается с увеличением объема работы, если ее нужно сделать за то же количество времени.

Если разделить 420 на 14, узнаем, что объем увеличивается в 30 раз.

Но так как по условию задачи на работу дается больше времени, то количество помощников увеличивается не в 30 раз. Таким образом:

Ответ: 20 человек напишут 420 постов за 12 дней.

Обратно пропорциональные величины

Две величины называют обратно пропорциональными, если при увеличении (или уменьшении) одной из них в несколько раз — другая уменьшается (или увеличивается) во столько же раз.

Объясним, что значит обратно пропорционально в виде схемы: «больше — меньше» или «меньше — больше».

Свойство обратной пропорциональности величин:

Если две величины находятся в обратно пропорциональной зависимости, то отношение двух произвольно взятых значений одной величины равно обратному отношению соответствующих значений другой величины.

Примеры обратно пропорциональной зависимости:

Формула обратной пропорциональности

где y и x — это переменные величины,

k — постоянная величина, которую называют коэффициентом обратной пропорциональности.

Коэффициент обратной пропорциональности — это произведение любых соответствующих значений обратно пропорциональных переменных y и x, равное одному и тому же числу.

Формула коэффициента обратной пропорциональности:

Потренируемся

Пример 1. 24 человека за 5 дней раскрутили канальчик в ютубе. За сколько дней выполнят ту же работу 30 человек, если будут работать с той же эффективностью?

Пример 2. Автомобиль проезжает от одного города до другого за 13 часов со скоростью 75 км/ч. Сколько времени ему понадобится, если он будет ехать со скоростью 52 км/ч?

Скорость и время связаны обратно пропорциональной зависимостью: чем больше скорость, тем меньше времени понадобится.

Соотношения равны, но перевернуты относительно друг друга.

Источник

«Пропорциональное деление»

Разделы: Математика

Тема урока: Пропорциональное деление

В школьном курсе математики предлагается очень мало задач на «пропорциональное деление». Однако их можно встретить в экзаменационных сборниках для 9 класса авт. Л.И.Звавич и др. Эти задачи предлагаются на вступительных экзаменах в ВУЗы на специальности, связанные с экономикой, химией, связанных с легкой промышленностью и народного хозяйства.
Предлагаемые задачи можно использовать на факультативах в общеобразовательных школах, включить их в программу гимназий и лицеев, связанных с углубленным изучением математики, начиная с 6 класса, для индивидуальной работы с сильными учениками.

Эти задачи может решить шестиклассник.

Необходимость разделить заданную величину или число в данном отношении часто возникает в практической жизни человека – при приготовлении различных смесей, растворов, блюд по кулинарным рецептам, при распределении прибыли или мест в парламенте и так далее.

Для приготовления строительного раствора на 2 части цемента берут 2 части песка и 0,8 частей воды. Сколько цемента, песка и воды потребуется для приготовления 180 кг раствора?

1) Пусть для приготовления строительного раствора требуется а кг цемента, b кг песка и с кг воды. Обозначим коэффициент пропорциональности k, тогда

Следовательно, а = 2k, b = 2k, c = 0,8k.
По условию задачи, сумма всех частей равна 180 кг, значит:
2k + 2k + 0,8k = 180 4,8k = 180 k = 37,5.
2) 37,5 • 2 = 75 (кг) – потребуется песка и цемента.
3) 37,5 • 0,8 = 30 (кг) – потребуется воды.
Ответ: потребуется 75 кг цемента, 75 кг песка и 30 кг воды.

Для краткого обозначения условия задач о прямо пропорциональном делении в математическом языке используют иногда «длинные отношения». Например, a : b : c = 2 : 2 : 0,8. При этом говорят : «Числа a, b и с относятся как 2 к 3 к 0,8».
Длинные отношения – это условные записи, которые показывают, сколько равных долей величины приходится на каждую часть. Их нельзя понимать как запись деления нескольких чисел. Действительно, подставив в последнее равенство вместо букв соответствующие им числа, получим верное высказывание 75 : 75 : 30 = 2 : 2 : 0,8;
Тогда как при непосредственном подсчете левой и правой части получаются разные числа: в левой части , а в правой части – 1,25.
Зато длинные отношения можно преобразовывать, как обычные дроби: умножать все его члены на одно и то же число, сокращать. Эти преобразования позволяют упрощать запись, а значит, и решение задач. Так, если бы в нашей задаче мы сначала умножили все члены отношения на 10, а затем разделили их на 4, то избавились бы от дробей: 2 : 2 : 0,8 = 20 : 20 : 8 = 5 : 5 : 2 и получили более простое уравнение.
Решая задачи на пропорциональное деление, мы вновь наблюдаем, как абстрактные математические понятия – в данном случае прямая и обратная пропорциональность – помогают отвечать на серьезные практические вопросы.

Предлагаю еще несколько задач по этой теме.

Задача 1.

Трое рабочих получили 4080 рублей. Суммы, полученные первым и вторым рабочими, относятся, как . Сумма, полученная третьим рабочим составляет того. Что получил первый рабочий. Сколько денег получил каждый рабочий?

Ответ: 2448 рублей получил первый рабочий; 571,2 рубля получил второй рабочий и 1060,8 рубля получил третий рабочий.

Задача 2.

Три цеха сшили 16800 пар обуви. Количество пар обуви сшитой первым и вторым цехами относятся как а третий цех сшил 75% того, что сшил первый цех. На сколько процентов выполнил план первый цех, если план каждого цеха был 4000 пар обуви?

Ответ: на 180% выполнил план первый цех.

Задача 3.

В палатку привезли свеклу, морковь, капусту. Количество свеклы и моркови равно отношению , а вес капусты составляет 250% от веса моркови. Капусты было на 80 кг больше, чем свеклы. Сколько килограммов каждого овоща привезли в палатку?

Ответ: в палатку привезли 120 кг свеклы; 80 кг моркови и 200 кг капусты.

Задача 4.

Магазин продал за 4 дня некоторое количество ткани. Количество ткани, проданной за первые три дня относились, как 0,9 : 1,4 : 1,3. В четвертый день продали 420 м ткани, что составило 28% всей ткани, проданной магазином за четыре дня. Сколько ткани продали за каждый день?

Ответ: магазин продал 270 м ткани за первый день; 520 м ткани за второй день; 390 м ткани за третий день и 420 м за четвертый день.

Задача 5.

Три класса собирали металлолом. Количество металлолома, собранного первым и вторым классами относится, как 4,5 : 3. Количество металлолома, собранного третьим классом составляет 40% того, что собрал первый класс. Сколько металлолома собрал каждый класс, если второй класс собрал на 0,8 тонны металлолома больше, чем третий класс?

Ответ: первый класс собрал 3 т металлолома, второй класс собрал
2 т металлолома, третий класс собрал 1,2 т металлолома.

Задача 6.

Ответ: 55 га земли вспахала первая бригада, 48 га земли спахала вторая бригада, 39,6 га земли вспахала третья бригада.

Предлагаю несколько задач для самостоятельного решения.

Задача 1.

Задача 2.

Магазин продавал муку в течение четырех дней. Количество муки, проданной за первые три дня, относится, как 1,8 к 2,8 к 2,6. В четвертый день продали 840 килограммов муки, что составляет 56% всей муки, проданной за четыре дня. Сколько муки продавали каждый день?

Задача 3.

Колхоз засыпал зерно в три склада. На первом складе было 40% всего зерна, засыпанного в три склада. Количество зерна, засыпанного во второй и третий склады, относится, как 16 к 21. Сколько зерна было на первом складе, если на третьем складе было на 450 ц больше, чем на втором.
Ответ: 2220 ц зерна было засыпано в первый склад.

Задача 4.

Три цеха изготовили 6500 деталей. Количество деталей, изготовленных первым и вторым цехами, относится, как 0,1875 к 0,25., количество деталей, изготовленных третьим цехом на 50% больше, чем количество деталей, изготовленных вторым цехом.. Сколько деталей изготовил каждый цех.

Задача 5.

Отряд отправился в поход из пункта А в пункт В. Первую часть пути школьники проехали на велосипедах, вторую часть пути прошли пешком, а оставшиеся 30 километров проплыли на лодке. Зная, что длины этих частей пути относятся, как 1,625 к 1,3 к 3, 25, определите длину всего маршрута.
Ответ: длина всего маршрута 57 километров.

Задача 6.

Из четырех чисел первые три относятся между собой, как , а четвертое составляет 40% от первого числа. Найти сумму всех четырех чисел, если первое больше суммы остальных на 40.

Продолжим решение задач.

Задача 7.

Найти сумму трех чисел, зная, что первое число равно 100, а первое число относится ко второму, как ; а второе к третьему, как •12 к 7.

Ответ: сумма трех чисел равна 385.

Задача 8.
Найти сумму трех чисел, зная, что первое число относится к третьему, как ; второе число относится к третьему как 5 к 2, а сумма первых двух чисел равна 500.

Ответ: сумма трех чисел равна 650.

Задача 9.

Найти каждое из трех чисел, если первое число относится ко второму как 0,6 : 0,75, а второе к третьему, как 1 : 0,9. Сумма первого и третьего чисел на 105 больше второго числа.

Задача 10.

Из данных четырех чисел первые три относятся, как , а четвертое составляет 15% второго числа. Найти эти числа, если известно, что второе число больше суммы остальных на 8.

Ответ : 48; 80; 12; 12.

Задача 11.

Задача 12.

Три колхоза построили хлебозавод. Суммы, внесенные колхозами в строительство, относятся, как . Сколько денег внес каждый колхоз, если стройматериалы стоят 1620 миллионов рублей, расход на рабочую силу составляет от стоимости материала, на оборудование израсходовали стоимости материала и рабочей силы вместе?

Ответ: на материалы – 2700 млн.рублей; на рабочую силу – 3600 млн.рублей; на оборудование – 4500 млн. рублей.

Источник

Прямая и обратная пропорциональность

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.

Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.

Прямая пропорциональность

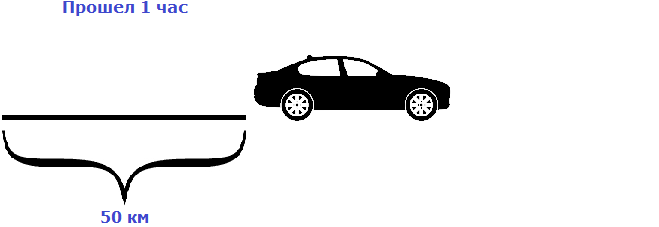
Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.

Изобразим на рисунке расстояние, пройденное автомобилем за 1 час

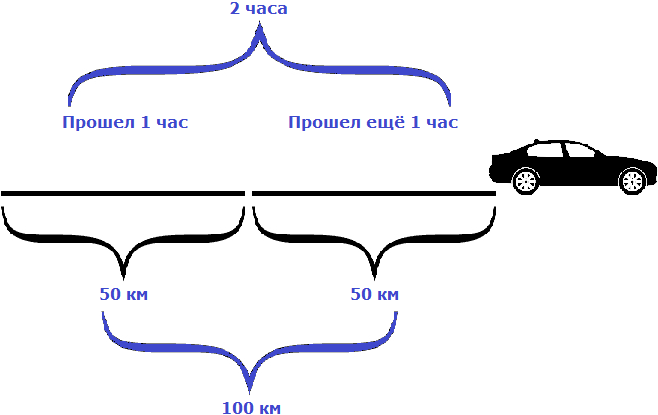
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км

Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.

Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.

Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.

Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.

Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.

В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.

Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50

Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.

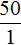
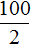
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:

Это отношение можно прочитать следующим образом:

Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.

Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.

Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.

Запишем чему равно отношение тридцати рублей к одному килограмму

Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:

Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.

Обратная пропорциональность

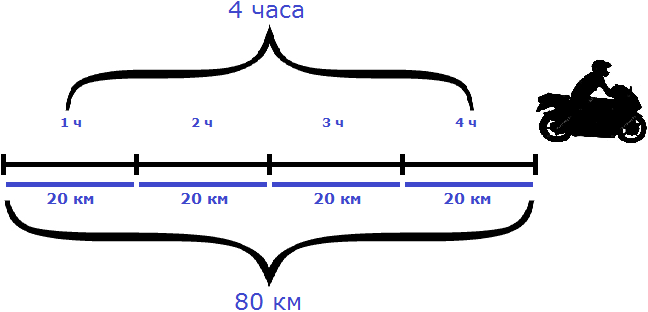
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.

Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:

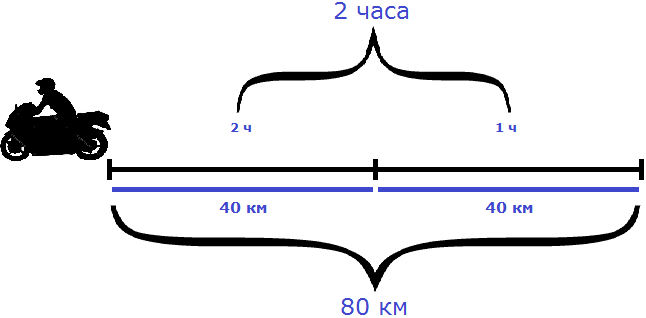
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.

Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.

Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.

Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.

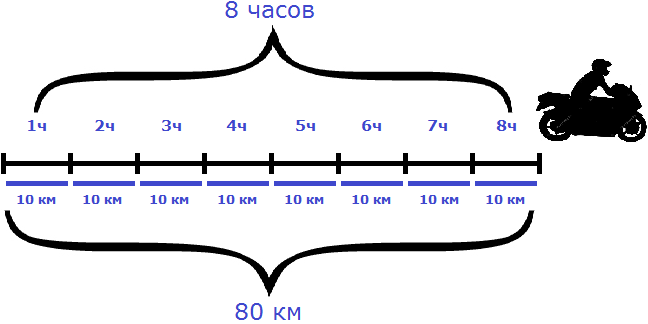
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:

Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.

Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.

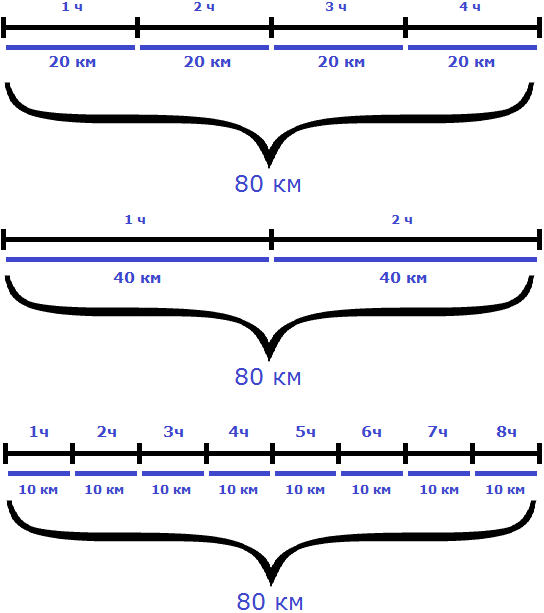
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным

Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

10 thoughts on “Прямая и обратная пропорциональность”

что ценно теория методически верно преподается. очень добрый сайт.

мне теперь всё понятно, большое спасибо сайту

Источник