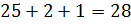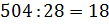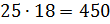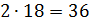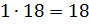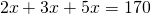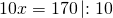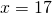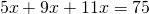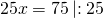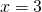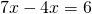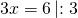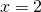Что значит разделить число в отношении

Математика. 6 класс

Конспект урока

Деление числа в данном отношении

Перечень вопросов, рассматриваемых в теме:

Частное двух не равных нулю чисел a и b называется отношением чисел a и b.

Числа a и b называются членами отношения.

Скорость – это отношение пройденного пути ко времени, за которое этот путь пройден.

Скорость сближения – это расстояние, на которое сближаются объекты за единицу времени.

Цена товара – это отношение стоимости товара к его массе или количеству единиц товара.

Теоретический материал для самостоятельного изучения

Сегодня мы с вами разберём, что означает деление числа в данном отношении.

Правило деления числа в данном отношении.

Чтобы разделить число c в отношении a к b, можно разделить число c на сумму членов отношения a + b и результат умножить на каждый член отношения, числа a, b и c не равны нулю.

Ответ: конфеты между друзьями надо разделить так: первому – 16 конфет, а второму – 64 конфеты.

Сестра и брат сложили свои деньги для покупки лотерейного билета. У сестры было 50 рублей, а у брата 30 рублей. Билет выиграл 4000 рублей. Как они должны разделить эти деньги между собой?

Ответ: 2500 рублей, 1500 рублей.

Трое хотят купить фирму по продаже мороженого. Первый желает иметь 6 частей акций, второй – 4 части акций, третий – 2 части. Всего нужно заплатить 960 000 рублей. Сколько денег должен внести каждый из них.

Ответ: 480 000 рублей, 320 000 рублей, 160 000 рублей.

Первая машинистка печатает 180 страниц за 20 часов, а вторая – за 30 часов. Как распределить между ними 180 страниц, чтобы они напечатали их в кратчайший срок?

Ответ: первой машинистке – 108 страниц, второй – 72 страницы.

Мотоциклист может проехать расстояние между пунктами за 4 часа, а велосипедист – за 12 часов. Однажды они одновременно отправились навстречу друг другу из этих пунктов. Сколько километров проедет каждый до встречи, если расстояние между пунктами 120 километров?

Разбор решения заданий тренировочного модуля

№1. Тип задания: сортировка элементов по категориям.

Поставьте в соответствующие столбцы числа, которые можно разделить нацело в заданных отношениях.

№2. Тип задания: подчеркивания.

Нужно подчеркнуть правильный вариант ответа.

Источник

Деление числа в данном отношении

На практике и в курсе математики довольно часто приходится делить число (величину) в данном отношении. Такие задачи решают на ЕГЭ, решали и в глубокой древности. Начнём с задачи из Древнего Египта.

Задача 1. Число и его половина составляют 9. Найдите число.

Решение. Пусть половина числа составляет 1 часть, тогда само число — 2 такие же части, так как число в 2 раза больше своей половины.

1) 1 + 2 = 3 (части) — приходится на число и его половину,

2) 9: 3 = 3 (единицы) — приходится на 1 часть, это половина числа,

3) 3 * 2 = 6 (единиц) — приходится на число.

Изменим условие задачи на части — получим задачу на деление числа в данном отношении.

Задача 2. Разделите число 9 в отношении 2: 1. Найдите полученные числа.

Решение задачи записано выше. Сделаем вывод в виде правила, которому можно следовать при решении других задач, меняя число и члены отношения.

Чтобы число 9 разделить в отношении 2: 1, надо это число разделить на сумму членов отношения и результат умножить на каждый член отношения.

Запишем решение задачи по новому правилу.

Решение. 1) 9: (2 + 1) * 2 = 6 — большее число,

2) 9: (2 + 1) * 1 = 3 — меньшее число.

Разумеется, меньшее число можно было найти вычитанием: 9 — 6 = 3.

Задача 3. Брат и сестра разделили 35 конфет в отношении 3: 4. Брату досталась меньшая часть. Сколько конфет досталось сестре?

Решение. 1) 35: (3 + 4) * 3 = 15 (конфет) — досталось брату,

2) 35 — 15 = 20 (конфет) — досталось сестре.

Задача 4. Малыш и Карлсон разделили 16 плюшек в отношении 3: 5. Сколько плюшек досталось Карлсону, если Малышу досталось меньше плюшек?

Решение. 1) 16: (3 + 5) * 3 = 6 (плюшек) — досталось Малышу,

2) 16 — 6 = 10 (плюшек) — досталось Карлсону.

Задача для ребят постарше.

Задача 5. В треугольнике три стороны имеют длину 8, 10 и 12. На какие отрезки биссектриса треугольника делит среднюю его сторону?

Решение. Биссектриса треугольника делит его сторону на части, пропорциональные двум другим сторонам треугольника, то есть в отношении 8: 12 = 2: 3. Разделим сторону 10 в отношении 2: 3.

1) 10: (2 + 3) * 2 = 4 — длина меньшей части,

2) 10 — 4 = 6 — длина большей части.

На ЕГЭ базового уровня в 2018 году была такая задача.

Задача 6. Маша и Медведь съели 110 печений и банку варенья, начав и закончив одновременно. Сначала Маша ела варенье, а Медведь — печенье, но в какой-то момент они поменялись. Медведь и то, и другое ест в три раза быстрее Маши. Сколько печений съел Медведь, если варенья они съели поровну?

Решение. Так как варенья они съели поровну, а Медведь ест варенье в 3 раза быстрее Маши, то на варенье Медведь потратил времени в 3 раза меньше, чем Маша. Печенье Медведь ел в 3 раза больше времени, чем Маша, которая в это время ела варенье. Так как скорость поедания печенья у Медведя в 3 раза больше, чем у Маши, то Медведь съел печенья в 3*3 = 9 раз больше, чем Маша. Делим 110 печений в отношении 9: 1.Медведь съел 110: (9 + 1)*9 = 99 (печений).

Авторы комментариев ФИПИ к результатам ЕГЭ отметили, что в группе хорошо подготовленных к сдаче экзамена на базовом уровне решили эту задачу менее половины выпускников, включенных в эту группу. При этом предполагалось, что задачу будут решать составлением уравнения. Как показано выше, задачу можно решить и арифметически.

Источник

Как разделить число в отношении

Как разделить число на части в данном отношении? Рассмотрим, как это сделать, на конкретных примерах.

1) Разделить число 170 на три части в отношении 2:3:5.

1)2+3+5=10 (частей) составляет все число.

2)170:10=17 — приходится на одну часть.

3)2∙17=34 — величина I части.

4)3∙17=51 — величина II части.

5)5∙17=85 — величина III части.

Пусть х — величина одной части. Поскольку мы делим число на пропорциональные части, величину одной части называют коэффициентом пропорциональности. Поэтому чаще всего сражу же пишут: пусть х — коэффициент пропорциональности. Тогда I часть равна 2х, II — 3х, III — 5х. Сумма трех частей равна числу:

Значит, I часть равна 2∙17=34, 3∙17=51, II — 3∙17=51, III — 5∙17=85.

2) Периметр треугольника равен 75 см, а стороны относятся как 5:9:11. Найти стороны треугольника.

Пусть х- коэффициент пропорциональности. Тогда стороны треугольника равны 5 см, 9х см и 11х см. По условию, периметр треугольника равен 75 см. Составим и решим уравнение:

Следовательно, стороны треугольника равны 5∙3=15 см, 9∙3=27 см, 11∙3=33 см.

Ответ: 15 см, 27 см, 33 см.

3) Настя и Лиза поделили конфеты в отношении 4:7. При этом у Лизы оказалось на 6 конфет больше. Сколько конфет было всего?

Пусть х — коэффициент пропорциональности. Тогда Насте досталось 4х конфет, Лизе — 7х конфет. Так как у Лизы конфет на 6 больше, чем у Насти, составляем уравнение:

Значит, количество конфет Насти 4∙2=8, Лизы — 7∙2=14, а всего у них 8+14=22 конфеты.

4 Comments

Решение последней (3й) задачи следует поправить, так в ней спрашивается общее количество конфет — 22.

Геннадий, спасибо, исправила.

Наверное, отношение стоимости 5 ручек к стоимости 4 тетрадей. 5 ручек стоят 5∙40=200 рублей, 4 тетради — 4∙70=280 рублей. Следовательно, отношение стоимости 5 ручек к стоимости 4 тетрадей равно 200/280=5/7.

Источник

Пропорциональное деление

Пропорциональное деление — деление какой-нибудь величины на части, прямо или обратно пропорциональные данным числам.

Чтобы разделить число на части пропорционально нескольким данным числам, надо разделить его на сумму этих чисел и частное умножить на каждое из них.

Деление числа на пропорциональные части

Пример 1. Разделить число 50 на части пропорционально числам 2 и 3.

Решение: Надо найти такие два слагаемых числа 50, которые будут относиться друг к другу так, как 2:3. Первое слагаемое должно содержать 2 части числа, а второе 3, значит, число 50 содержит 5 таких частей (2 + 3 = 5), следовательно, каждая такая часть будет равна:

Число 10 — одна часть. Теперь надо умножить эту часть на числа, пропорционально которым требовалось разделить число 50:

Пример 2. Разделить число 90 на три слагаемых пропорционально числам 1, 2 и 3.

90 : (1 + 2 + 3) = 90 : 6 = 15;

Длинные отношения вида 1:2:3 называются сложными. Сложные отношения — это условные записи, показывающие, сколько долей содержит каждая часть. Если члены сложного отношения дробные, то, приведя их к общему знаменателю и умножив на него, можно заменить отношение дробных чисел отношением целых.

Пример. Разделить число 66 на такие три части, чтобы первая относилась ко второй, как 3:2, а вторая к третьей, как 5:4.

Первый способ: обозначим искомые части буквами a, b и c. Так как отношение не изменится, если оба члена умножить на одно и то же число, то умножим члены первого отношения на 5, а второго на 2:

значит a:b:c = 15:10:8. Так как 15 + 10 + 8 = 33, то

Второй способ: обозначим искомые части буквами a, b и c:

Если первая часть a равна 3, вторая b равна 2, то третью часть c можно определить из пропорции:

Следовательно, c равно:

Умножив все члены полученного сложного отношения на 5, чтобы избавиться от дробного члена, получим:

так как 15 + 10 + 8 = 33, то

Деление на части, обратно пропорциональные числам

Пример. Разделить число 62 на три части обратно пропорционально числам 2, 3 и 5, то есть разложить на три части, которые относились бы между собой, как

Решение: Обозначим искомые части буквами a, b и c. Приведём члены отношения к общему знаменателю и заменим дробные члены на целые числа:

Источник

Деление числа в данном отношении

Урок 23. Математика 6 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Деление числа в данном отношении»

Представим себе такую историю…

– Саша, чем ты занимаешься? – поинтересовался у друга Паша.

– Хочу приготовить мороженое, – ответил Саша. – Уже и рецепт нашёл, и подготовил все ингредиенты, но вот только разобраться не могу, сколько чего брать.

– А что в рецепте написано? – уточнил Паша.

– В рецепте сказано, что для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара, – прочитал Саша. – А как эти части высчитать, если я хочу приготовить, например, 3 килограмма мороженого?

– И вправду, сложная задача у тебя получается, – задумался Паша. – Как эти части считать, не понятно. Но я знаю, кто нам сможет помочь!

– Ребята, прежде чем я отвечу на ваш вопрос, давайте немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Давайте сверимся! – сказал Мудряш. — Посмотрите, что у вас должно было получиться!

– Ну а теперь вернёмся к вашему вопросу, – начал Мудряш. – Чтобы ответить на вопрос «Сколько каких ингредиентов нужно взять для приготовления смеси мороженого?», прежде всего нужно научиться выполнять деление числа в данном отношении. Итак, вы хотите приготовить 3 килограмма мороженого. Для удобства давайте переведём килограммы в граммы, всё же так будет легче и привычнее считать.

– Так как 1 килограмм равен 1000 грамм, – стал размышлять Саша, – значит, я хочу приготовить 3000 грамм мороженого.

– Хорошо! – согласился Мудряш. – По рецепту для приготовления мороженого нужно смешать 3 части молока, 2 части сливок и 1 часть сахара. Будем считать, что смесь мороженого состоит из 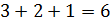частей, имеющих одинаковые массы. Тогда как посчитать, сколько приходится на 1 часть?

– Нужно 3000 разделить на 6, – ответил Паша.

– Правильно! – сказал Мудряш. – Значит, масса одной части смеси равна 500 граммам. По рецепту молоко в смеси составляет 3 части, сливки – 2 части, а сахар – 1 часть. Посчитайте, чему же будут равны эти части.

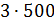
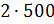
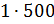
– Тогда масса молока в смеси будет равна и равна 1500 граммам, – принялся считать Саша. – Масса сливок будет равна и равна 1000 грамм, а масса сахара будет равна и равна 500 граммам.

– Получается, что для приготовления 3 килограммов мороженого нужно взять 1500 грамм молока, добавить 1000 грамм сливок, а затем добавить 500 грамм сахара? – решил уточнить Паша.

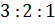
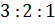
– Всё верно! – согласился Мудряш. – Из решения вашей задачи следует, что число 3000 можно представить в виде суммы трёх слагаемых – 1500, 1000 и 500, отношение которых равно . В таких случаях говорят, что число 3000 разделили в отношении . Также можно сказать, что число 3000 представили в виде суммы трёх слагаемых, пропорциональных числам 3, 2 и 1.

– И совсем несложная задача оказалась, – заметил Саша. – Теперь я без труда могу приготовить мороженое.

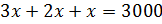
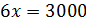
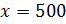
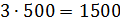
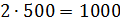
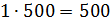
– Эту же задачу можно было решить и другим способом, – продолжил Мудряш. – Пусть масса одной части смеси мороженого составляет х грамм. Тогда массы молока, сливок и сахара составляют соответственно 3х грамм, 2х грамм и х грамм. Поскольку масса всей смеси мороженого равна 3000 грамм, то можем составить уравнение . Решим это уравнение. Получим, что . Отсюда . Тогда массы молока, сливок и сахара равны соответственно грамм, грамм и грамм.

– Сделаем вывод, – сказал Мудряш. – Чтобы разделить число в данном отношении, можно разделить это число на сумму членов отношения, а затем результат умножить на каждый член отношения.

– А теперь, ребята, давайте посмотрим, как вы всё поняли, и выполним несколько заданий.

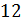
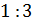
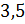
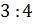
Задание первое: разделите числа в указанных отношениях: а) число в отношении ; б) число в отношении .

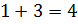
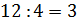
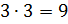
Решение: нужно разделить число 12 в отношении 1 к 3. Будем считать, что всё число состоит из частей. Значит, 1 часть равна . Тогда 3 части будут равны . Следовательно, число двенадцать можно разделить в отношении 1 к 3 так: 3 и 9.

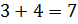
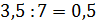
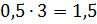
В следующем условии нам нужно разделить число 3,5 в отношении 3 к 4. Будем считать, что всё число состоит из частей. Тогда 1 часть равна . Отсюда 3 части числа равны . Следовательно, число 3,5 можно разделить в отношении 3 к 4 так: 1,5 и 2.

Следующее задание: два числа относятся как 4 к 7. Найдите эти числа, зная, что: их сумма равна 110, их разность равна 12.

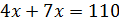
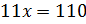
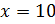
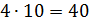
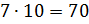
Решение: обозначим за х одну часть. Тогда можем записать, что первое число равно 4х, второе – 7х. В первом условии сказано, что сумма этих чисел равна 110. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

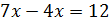
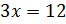
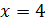
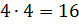
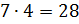
Во втором условии сказано, что разность этих чисел равна 12. Составим уравнение . Решим его. Получим . Отсюда . Значит, первое число равно , второе – .

Решим задачу: стороны прямоугольника 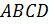относятся как 2 к 3. Найдите площадь этого прямоугольника, если его периметр равен 20 сантиметров.

И решим ещё одну задачу. Для приготовления фарфора смешивают 25 частей белой глины, 2 части песка и 1 часть гипса. Сколько нужно взять каждого материала, чтобы приготовить 504 грамма смеси?

Решение: будем считать, что вся смесь состоит из частей, имеющих одинаковые массы. Тогда 1 часть содержит грамм. Следовательно, чтобы приготовить 504 грамма смеси фарфора, нужно взять: грамм белой глины, грамм песка и грамм гипса.

Источник