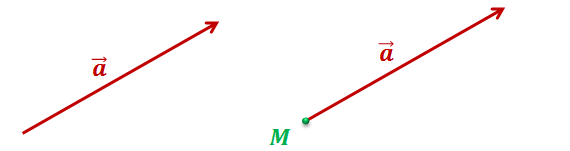
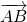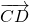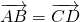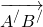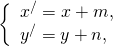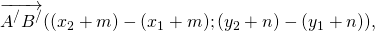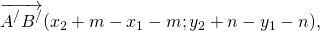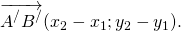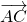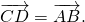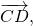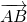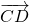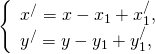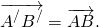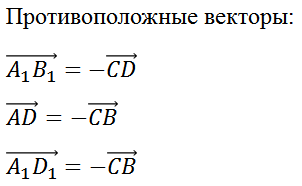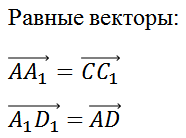Что значит равные векторы
Равные векторы
В различных школьных учебниках определение равных векторов даётся по-разному.
В классическом учебнике Погорелова А. В. понятие равных векторов вводится с помощью параллельного переноса.
Два вектора называются равными, если они совмещаются параллельным переносом.
(то есть существует параллельный перенос, который переводит начало и конец одного вектора соответственно в начало и конец другого).

Равенство векторов обозначают так:
(Свойства равных векторов)
1) Равные векторы сонаправлены и имеют равные длины.
2) Равные векторы имеют равные координаты.
3) От любой точки можно отложить вектор, равный данному, и притом только один.
1) 1-е свойство вытекает непосредственно из определения равных векторов и свойств параллельного переноса.
2) Пусть дан вектор
с началом в точке A(x1; y1) и концом в точке B(x2; y2).
По определению равных векторов, вектор
равный данному, получен из
Если этот параллельный перенос задан формулами
Найдём координаты каждого из векторов:
То есть координаты равных векторов
Что и требовалось доказать.
Таким образом, координаты задают длину и направление вектора, но не фиксируют его.
3) Пусть даны вектор
и точка C.
Существует и притом единственный параллельный перенос, при котором точка A переходит в точку C — параллельный перенос на вектор
При таком параллельном переносе вектор
переходит в вектор
По определению равных векторов,
Что и требовалось доказать.
На практике, если требуется отложить от некоторой точки вектор, равный данному, удобно это делать с помощью параллелограмма (если точка, от которой откладывается вектор, не лежит на прямой, содержащей этот вектор).
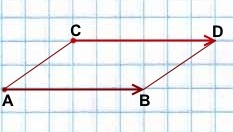
отложенный от точки C, равен вектору
(Признаки равенства векторов)
1) Если векторы сонаправлены и имеют одинаковые длины, то они равны.
2) Если у векторов соответствующие координаты равны, то векторы равны.
1) 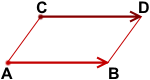
сонаправлены и имеют одинаковые длины.
Параллельный перенос, который переводит точку A в точку C, совмещает луч CD с лучом AB (поскольку векторы одинаково направлены). А так как длины отрезков CD и AB равны, то точка D при этом совместится с точкой B. Таким образом, этот параллельный перенос вектор
переводит в вектор
По определению равных векторов,
Что и требовалось доказать.
Параллельный перенос, заданный формулами
переводит точку A в точку A′, точку B — в точку B′, то есть совмещает векторы
А это означает, что
Что и требовалось доказать.
В учебнике Атанасяна Л. С. и др. дано другое определение равных векторов.
Два вектора называются равными, если они сонаправлены и имеют одинаковую длину.
Равенство векторов
Урок 33. Геометрия 10 класс ФГОС
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Равенство векторов»
На прошлых занятиях мы ввели понятие вектора в пространстве.
Отрезок, для которого указано, какой из его концов является началом, а какой — концом, называется вектором. Любая точка пространства также является вектором, нулевым вектором.
Мы выяснили, что длина ненулевого вектора 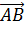
Так же дали определение коллинеарным векторам. Это векторы, которые лежат на одной прямой или на параллельных прямых.
Если коллинеарные векторы имеют одинаковое направление, то они являются сонаправленными. Если же их направления противоположны, то векторы называют противоположно направленными.
На этом уроке мы будем говорить о равных векторах. Определение равных векторов в пространстве звучит так же, как и определение равных векторов на плоскости.
Равными называют сонаправленные векторы, длины которых равны.
Ну, а противоположно направленные векторы, длины которых равны, называют противоположными.
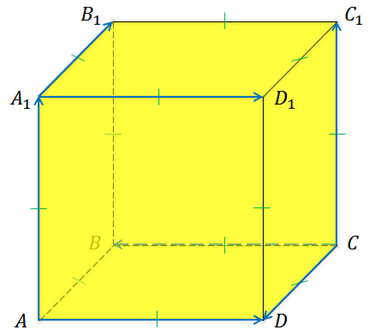
На рисунке изображён куб ABCDA1B1C1D1. Среди векторов, показанных на рисунке, найдём пары равных и противоположных векторов.
Перед нами куб, и стоит вспомнить, что это за фигура. Это многогранник, все грани которого являются квадратами. Значит, все рёбра куба равны между собой.
Векторы 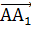
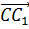
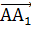
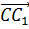
Векторы 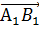
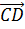
Векторы 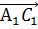
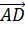
Векторы 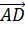
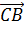
Также противоположно направленными и равными по длине будут векторы 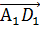
Так мы с вами выписали две пары равных векторов и три пары противоположных векторов.
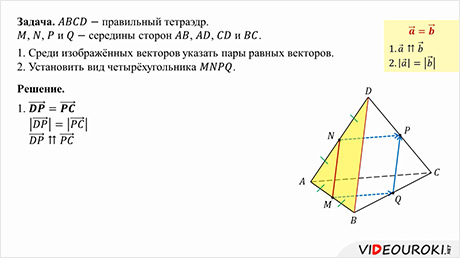
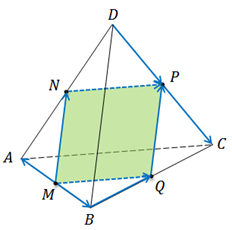
Задача. 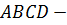
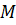
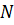
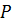
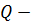
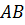
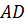
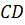
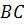
1. Среди изображённых векторов указать пары равных векторов.
2. Установить вид четырёхугольника 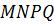
Равными являются сонаправленные векторы, длины которых равны.
А для того чтобы векторы были сонаправлены, они должны быть коллинеарны. То есть должны лежать на параллельных прямых или на одной прямой.
Никакие рёбра тетраэдра не являются параллельными. Поэтому на рёбрах будем искать векторы, лежащие на одной прямой. Такими являются векторы 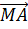
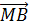
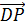
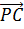
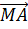
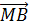
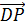
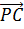
Но векторы 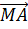
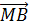
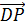
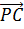
Так мы нашли одну пару равных векторов, 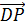
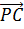
Далее рассмотрим треугольник ABD. Точки М и N — середины сторон AB и AD. Значит, МN — средняя линия. И она параллельна стороне BD, а также равна её половине.
В треугольнике CBD отрезок PQ является средней линией. Он параллелен стороне BD и равен её половине.
Так мы получаем, что отрезки МN и PQ параллельны и равны. Значит, векторы 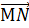
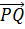
Аналогично, в треугольнике ADC отрезок NP является средней линией. Он параллелен стороне AC и равен её половине.
В треугольнике ABC отрезок MQ также является средней линией. Он параллелен стороне AC и равен её половине.
Отсюда получаем, что отрезки NP и MQ параллельны и равны. А значит, можем сделать вывод о равенстве векторов 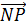
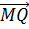
Так мы с вами нашли три пары равных векторов.
Теперь осталось определить вид четырёхугольника MNPQ.
Нами уже установлено, что противоположные стороны этого четырёхугольника параллельны и равны. А это говорит о том, что данный четырёхугольник является параллелограммом.
Но так как все рёбра данного тетраэдра равны, то равны и длины средних линий, рассматриваемых ранее треугольников.
Получаем, что MNPQ — параллелограм, все стороны которого равны между собой. А значит, данный четырёхугольник является ромбом.
Ответ. 1) 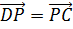
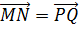
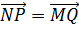
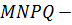
Далее вспомним, что от любой точки плоскости можно отложить вектор равный данному, и притом только один.
Это утверждение верно и для любой точки пространства.
Действительно, если рассмотреть некоторый вектор 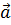
В полученной плоскости отложим от точки М вектор 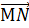
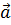
Говорят «вектор 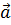
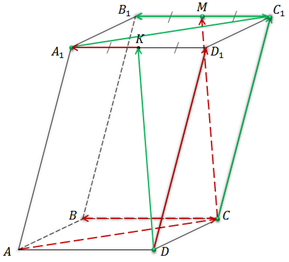
В параллелепипеде ABCDA1B1C1D1 точки K и М — середины сторон A1D1 и B1C1 соответственно. Стоит напомнить, что все грани параллелепипеда являются параллелограммами, а их противоположные стороны равны. Значит, равны и их половины.
Итак, нам нужно назвать векторы, которые получатся, если от данной точки отложить вектор, равный данному.
Первым нам нужно назвать вектор, который получится, если от точки C отложить вектор, равный вектору 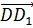
Нам известно, что от точки пространства можно отложить только один вектор, равный данному.
Вектор 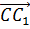
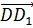
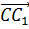
Далее назовём вектор, который получится, если от точки D отложить вектор, равный вектору 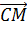
Вектор 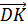
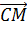
Так, если от точки А1 отложить вектор, равный вектору 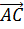
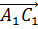
Если же от точки C1 отложить вектор, равный вектору 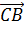
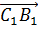
И, отложив от точки М вектор, равный вектору 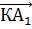
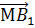
Подведём итоги урока.
На этом уроке мы выяснили, что, так же как и на плоскости, в пространстве равными называют сонаправленные векторы, длины которых равны.
Если же векторы противоположно направлены и их длины равны, то такие векторы называют противоположными.
Так же мы отметили, что от любой точки пространства можно отложить вектор, равный данному вектору, и притом только один.
Всем этим знаниям мы нашли применение при решении задач.