Что значит равны по модулю
Что значит равны по модулю
ВНИМАНИЕ! В связи с новой волной пандемии и шумом вокруг вакцинации агрессивные антивакцинаторы банятся без предупреждения, а их особенно мракобесные комментарии — скрываются.
Основные условия публикации
— Посты должны иметь отношение к науке, актуальным открытиям или жизни научного сообщества и содержать ссылки на авторитетный источник.
— Посты должны по возможности избегать кликбейта и броских фраз, вводящих в заблуждение.
— Научные статьи должны сопровождаться описанием исследования, доступным на популярном уровне. Слишком профессиональный материал может быть отклонён.
— Видеоматериалы должны иметь описание.
— Названия должны отражать суть исследования.
— Если пост содержит материал, оригинал которого написан или снят на иностранном языке, русская версия должна содержать все основные положения.
Не принимаются к публикации
— Точные или урезанные копии журнальных и газетных статей. Посты о последних достижениях науки должны содержать ваш разъясняющий комментарий или представлять обзоры нескольких статей.
— Юмористические посты, представляющие также точные и урезанные копии из популярных источников, цитаты сборников. Научный юмор приветствуется, но должен публиковаться большими порциями, а не набивать рейтинг единичными цитатами огромного сборника.
— Посты с вопросами околонаучного, но базового уровня, просьбы о помощи в решении задач и проведении исследований отправляются в общую ленту. По возможности модерация сообщества даст свой ответ.
— Оскорбления, выраженные лично пользователю или категории пользователей.
— Попытки использовать сообщество для рекламы.
— Многократные попытки публикации материалов, не удовлетворяющих правилам.
— Нарушение правил сайта в целом.
Окончательное решение по соответствию поста или комментария правилам принимается модерацией сообщества. Просьбы о разбане и жалобы на модерацию принимает администратор сообщества. Жалобы на администратора принимает @SupportComunity и общество пикабу.
Модуль числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение модуля числа
Алгебра дает четкое определение модуля числа. Модуль в математике — это расстояние от начала отсчёта до точки координатной прямой, соответствующей этому числу.
Если мы возьмем некоторое число «a» и изобразим его на координатной прямой точкой A — расстояние от точки A до начала отсчёта (то есть до нуля) длина отрезка OA будет называться модулем числа «a».
Знак модуля: |a| = OA.
Разберем на примере:
Точка В, которая соответствует числу −3, находится на расстоянии 3 единичных отрезков от точки O (то есть от начала отсчёта). Значит, длина отрезка OB равна 3 единицам.
Число 3 (длину отрезка OB) называют модулем числа −3.
Обозначение модуля: |−3| = 3 (читают: «модуль числа минус три равен трём»).
Точка С, которая соответствует числу +4, находится на расстоянии четырех единичных отрезков от начала отсчёта, то есть длина отрезка OС равна четырем единицам.
Число 4 называют модулем числа +4 и обозначают так: |+4| = 4.
Также можно опустить плюс и записать значение, как |4| = 4.
Записывайся на занятия по математике для учеников с 1 по 11 классы.
Свойства модуля числа
Давайте рассмотрим семь основных свойств модуля. Независимо от того, в какой класс перешел ребенок — эти правила пригодятся всегда.
1. Модуль числа — это расстояние, а расстояние не может быть отрицательным. Поэтому и модуль числа не бывает отрицательным:
2. Модуль положительного числа равен самому числу.
3. Модуль отрицательного числа равен противоположному числу.
4. Модуль нуля равен нулю.
5. Противоположные числа имеют равные модули.
6. Модуль произведения равен произведению модулей этих чисел.
Геометрическая интерпретация модуля
Как мы уже знаем, модуль числа — это расстояние от нуля до данного числа. То есть расстояние от точки −5 до нуля равно 5.
Нарисуем числовую прямую и отобразим это на ней.
Эта геометрическая интерпретация используется для решения уравнений и неравенств с модулем. Давайте рассмотрим на примерах.
Решим уравнение: |х| = 5.
Мы видим, что на числовой прямой есть две точки, расстояние от которых до нуля равно 5. Это точки 5 и −5. Значит, уравнение имеет два решения: x = 5 и x = −5.
График функции
График функции равен y = |х|.
Для x > 0 имеем y = x.
Этот график можно использовать при решении уравнений и неравенств.
Корень из квадрата
Оно равно a при а > 0 и −а, при а
Модуль комплексного числа
Чему равен модуль числа в данном случае? Это арифметический квадратный корень из суммы квадратов действительной и мнимой части комплексного числа:
Свойства модуля комплексных чисел
Модуль рационального числа
Как найти модуль рационального числа — это расстояние от начала отсчёта до точки координатной прямой, которая соответствует этому числу.
Модуль рационального числа, примеры:
Модуль вещественных чисел
Модуль противоположного числа, нуля, отрицательного и положительного чисел
Закрепим свойства модуля числа, которые мы рассмотрели выше:
Сравнение чисел по модулю
Определение 1. Если два числа 1 ) a и b при делении на p дают один и тот же остаток r, то такие числа называются равноостаточными или сравнимыми по модулю p.
Утверждение 1. Пусть p какое нибудь положительное число. Тогда всякое число a всегда и притом единственным способом может быть представлено в виде
1 ) В данной статье под словом число будем понимать целое число.
Действительно. Если s получит значение от −∞ до +∞, то числа sp представляют собой совокупность всех чисел, кратных p. Рассмотрим числа между sp и (s+1)p=sp+p. Так как p целое положительное число, то между sp и sp+p находятся числа
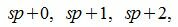 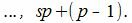 |
Но эти числа можно получить задав r равным 0, 1, 2. p−1. Следовательно sp+r=a получит всевозможные целые значения.
Покажем, что это представление единственно. Предположим, что p можно представить двумя способами a=sp+r и a=s1p+r1. Тогда
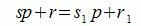 |
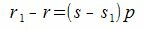 | (2) |
Число r называется вычетом числа a по модулю p (другими словами, число r называется остатком от деления числа a на p).
Утверждение 2. Если два числа a и b сравнимы по модулю p, то a−b делится на p.
Действительно. Если два числа a и b сравнимы по модулю p, то они при делении на p имеют один и тот же остаток p. Тогда
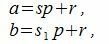 |
где s и s1 некоторые целые числа.
Разность этих чисел
 | (3) |
делится на p, т.к. правая часть уравнения (3) делится на p.
Утверждение 3. Если разность двух чисел делится на p, то эти числа сравнимы по модулю p.
Доказательство. Обозначим через r и r1 остатки от деления a и b на p. Тогда
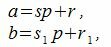 |
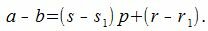 |
По утверждению a−b делится на p. Следовательно r−r1 тоже делится на p. Но т.к. r и r1 числа 0,1. p−1, то абсолютное значение |r−r1| Свойство 1. Для любого a и p всегда
Действительно. Из условия свойства 2 следует a−b и b−c делятся на p. Тогда их сумма a−b+(b−c)=a−c также делится на p.
| a≡b mod (p) и m≡n mod (p), |
| a+m≡b+n mod (p) и a−m≡b−n mod (p). |
Действительно. Так как a−b и m−n делятся на p, то
также делятся на p.
Это свойство можно распространить на какое угодно число сравнений, имеющих один и тот же модуль.
| a≡b mod (p) и m≡n mod (p), |
Действительно.Так как a−b делится на p, то (a−b)m также делится на p, следовательно
Далее m−n делится на p, следовательно b(m−n)=bm−bn также делится на p, значит
Таким образом два числа am и bn сравнимы по модулю с одним и тем же числом bm, следовательно они сравнимы между собой (свойство 2).
где k некоторое неотрицательное целое число.
Действительно. Имеем a≡b mod (p). Из свойства 4 следует
| a·a≡b·b mod (p). |
| a·a·a≡b·b·b mod (p). |
| . |
| a k ≡b k mod (p). |
Все свойства 1-5 представить в следующем утверждении:
При делении все обстоит иначе. Из сравнения
не всегда следует сравнение
Утверждение 5. Пусть
Доказательство. Пусть λ наибольший общий делитель чисел m и p. Тогда
Так как m(a−b) делится на k, то
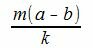 |
имеет нулевой остаток. Тогда
 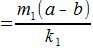 . . |
 |
имеет нулевой остаток, т.е. m1(a−b) делится на k1. Но числа m1 и k1 числа взаимно простые. Следовательно a−b делится на k1=k/λ и, тогда, a≡b mod (p/λ).
Утверждение 6. Если
и m является один из делителей числа p, то
Действительно. a−b делится на p. p делится на m. Следовательно a−b делится на m.
Утверждение 7. Если
| a≡b mod (p), a≡b mod (q), a≡b mod (s) |
где h наименьшее общее кратное чисел p,q,s.
Действительно. Разность a≡b должна быть числом, кратным p,q,s. и, следовательно должна быть кратным h.
В частном случае, если модули p,q,s взаимно простые числа, то
Заметим, что можно допустить сравнения по отрицательным модулям, т.е. сравнение a≡b mod (p) означает и в этом случае, что разность a−b делится на p. Все свойства сравнений остаются в силе и для отрицательных модулей.
Законы Ньютона
Ньютон первым обратил внимание на силу, как причину, по которой тела приходят в движение и меняют свою скорость.
Раздел механики, изучающий силы, называется динамикой. По-гречески «динамис», значит «сила».
Что такое сила
Тела действуют друг на друга с помощью сил.
Сила – это мера взаимодействия тел. Измеряя силу, мы измеряем величину взаимного действия тел. В обыденной жизни мы говорим: «как сильно» одно тело действует на другое тело.
Смысл законов Ньютона
Ньютон, в своих законах динамики, хотел сказать следующее:
Примечание:
Выражение «векторы равны по модулю», понимаем так: «длины векторов одинаковые».
Перед изучением законов Ньютона рекомендую вспомнить, что такое инерциальные системы отсчета (откроется в новой вкладке).
Первый закон Ньютона
Словесная формулировка первого закона Ньютона:
В инерциальной системе отсчета тело свою скорость не меняет, если на него не действуют другие тела (или действие других тел скомпенсировано).
Формула:
\( F = 0 \) – сила на тело не действует (Может быть и так: на тело действуют несколько сил, но их действие компенсируется);
\( a = 0 \) – ускорение отсутствует;
\( v = const \) – скорость тела не изменяется (остается одной и той же);
\( p = const \) – импульс тела не изменяется (остается одним и тем же);
Важно! По первому закону Ньютона, «двигаться с одной и той же скоростью по прямой» и «покоиться» — это равнозначные виды движения.
Значит, если на тело не действуют другие тела (силы), то
Второй закон Ньютона
Сформулируем словами второй закон Ньютона:
Ускорение, приобретаемое телом,
прямо пропорционально
приложенной силе
и обратно пропорционально
массе этого тела.
Формула второго закона Ньютона с пояснениями
\( a \left( \frac<\text<м>>
\( m \left( \text <кг>\right) \) – масса тела
\( F \left( H \right) \) – сила, которую приложили к телу
Примечание: Ускорение отвечает на вопрос: «Как быстро меняется скорость тела?». Значит, если изменяется хотя бы одна из характеристик вектора скорости, ускорение есть. А если скорость не изменяется, ускорения нет \( \vec < a >= 0 \)
Ускорение прямо пропорционально силе:
Чем больше сила, тем больше ускорение тела, тем быстрее тело меняет скорость.
Ускорение обратно пропорционально массе:
Чем больше месса тела, тем труднее изменить его скорость.
Формулу второго закона часто записывают в векторном виде:
Мы можем заменить местами правую и левую части, в таком случае получим:
Расшифруем эту запись: Возьмем вектор «F», умножим его на скаляр (1/m) и получим новый вектор «a».
Дробь \( \displaystyle \frac<1>
Примечания:
Третий закон Ньютона
Пусть одно тело действует на второе тело. Тогда это второе тело будет в ответ действовать на первое.
Словами третий закона Ньютона можно сформулировать так:
Силы взаимного действия по модулю равны, а направлены противоположно. Они лежат на прямой, которая соединяет центры тел, действующих друг на друга.
\( F_ <12>\left( H \right) \) – сила, с которой первое тело действует на второе тело.
\( F_ <21>\left( H \right) \) – сила, с которой второе тело отвечает первому.
Пояснить формулу можно с помощью такого рисунка:
Обратите внимание, что длины красного и черного векторов равны.
Не важно, перед каким из векторов находится знак «минус». Этот знак показывает, что векторы направлены в противоположные стороны. Поэтому, формулу третьего закона Ньютона можно записать и так:
Примечания:
Советую прочитать еще две статьи. Так как для решения задач кроме знания трех законов Ньютона нужно дополнительно уметь:
Конспект «теория сравнения по модулю»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Муниципальное бюджетное общеобразовательное учреждение
Семлевская средняя общеобразовательная школа №1
Вяземского района Смоленской области
Научно-исследовательская работа по теме
«Теория сравнения по модулю»
Подготовила
ученица 9 класса: Попова Анастасия
Преподаватель: Перцева С.М.
Понятие модуля числа известно каждому, а вот что означает понятие сравнение по модулю, знают далеко не все. Тема моей работы «Теория сравнения по модулю». Я обратилась к этой теме, так как она недостаточно полно изложена в действующих учебниках математики, а задачи по этой теме предлагаются как на олимпиадах, так и на вступительных экзаменах в вузы.
1) Изучить краткий исторический обзор возникновения теории;
2) Дать определение сравнения по модулю;
3) Изучить свойства сравнения по модулю;
4) Рассмотреть операции со сравнениями;
5) Применить знания для решения практических заданий.
1)Теоретический анализ и обобщение научной литературы;
2)Математический расчет;
Если два целых числа 



Сравнимость чисел 

Число 
Определение сравнимости чисел 


Разность чисел 


Число 


Например : 32 и −10 сравнимы по модулю 7, так как оба числа при делении на 7 дают остаток 4:
Также, 32 и −10 сравнимы по модулю 7, так как их разность 42 делится на 7, и к тому же имеет место представление:




