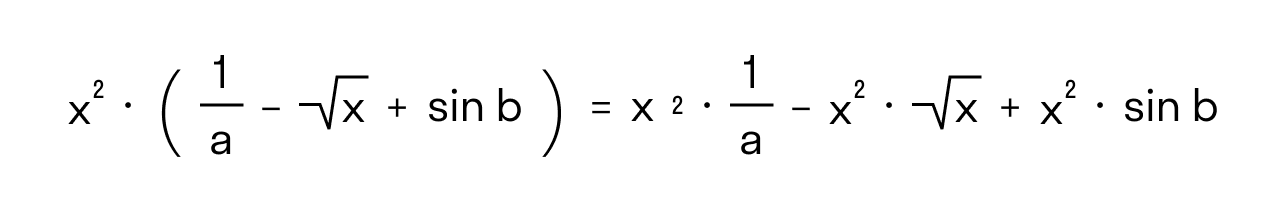Что значит раскрыть скобки
Раскрытие скобок: правила и примеры

Раскрытие скобок: правила
Правило раскрытия скобок при сложении
Если перед скобками стоит плюс, то скобки просто опускаются.
Иными словами, скобки исчезнут, а то, что было в скобках, запишется без изменений.
Например, (a−b) = a−b.
В данном правиле следует учитывать, что в математике не принято писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа 2 и 3, то запишем 2+3, а не +2+3. Значит перед скобками, которые стоят в начале выражения, стоит плюс, который не пишут.
Пример 1: 8+(5−3) = 10. Ответ: 8+5–3 = 10.
Пример 2: 6+(−1+2) = 7. Ответ: 6–1+2 = 7.
Пример 3: 8a + (3b −6a). Ответ: 8a + 3b −6a = 2a + 3b.
Правило раскрытия скобок при вычитании
Если перед скобками стоит минус, то скобки опускаются, а каждое слагаемое внутри нее меняет свой знак на противоположный.
Например, −(a−b) = −a+b
Пример 1: 8–(5–3) = 6. Ответ: 8 – 5 + 3 = 6.
Пример 2: 6 − (−1 + 2) = 5. Ответ: 6 + 1 – 2 = 5.
Пример 3: 8a–(3b −6a). Ответ: 8a – 3b + 6a = 14a – 3b.
Пример 4: −(5b −2). Ответ: −5b +2.
Раскрытие скобок при умножении
Если перед скобками стоит знак умножения, то каждое число внутри скобок умножается на множитель, стоящий перед скобками.
При этом умножение минуса на минус дает плюс, а умножение минуса на плюс дает минус.
Данное правило основано на распределительном законе умножения: a(b+c) = ab + ac.
Пример 1: 8×(5 − 3) = 16. Ответ: 8 ×5 − 8 ×3 = 16.
Пример 2: a×(7 +2). Ответ: a×7+a×2 = 7a + 2a = 9a.
Пример 3: 8×(3b −6a). Ответ: 8×3b – 8×6a = 24b–48a
Раскрытие скобок при делении
Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок.
Пример 1: (25−15):5. Ответ: 25:5−15:5= 2.
Пример 2: (−14a +10):2. Ответ: −14a:2 +10:2 = −7a +5.
Пример 3: (36b + 6a):6. Ответ: 36b:6 + 6a:6 = 6b + a.
Раскрытие скобок при умножении двух скобок
При умножении скобки на скобку, каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.
Например, (c+d) × (a−b) = c×(a−b)+d×(a−b) = ca−cb+da−db
Пример. Раскрыть скобки: (2−a) × (3a−1).
Решение:
Шаг 1. Убираем первую скобку (каждое ее слагаемое умножаем на вторую скобку): 2 × (3a−1) − a × (3a−1).
Шаг 2. Раскрываем произведение скобок: (2×3a− 2×1) – (a×3a−a×1) = 2×3a− 2×1 – a×3a + a×1.
Шаг 3. Перемножаем и приводим подобные слагаемые: 6a–2–3a2+a = 7a–2–3a2
Раскрытие вложенных скобок
Иногда встречаются примеры со скобками, которые вложены в другие скобки. Чтобы решить такую задачу, нужно сначала раскрыть внутреннюю скобку (при этом остальное выражение оставить без изменений), а потом внешнюю скобку.
Пример 1. 7a + 2 × (5− (3a+b)).
Решение:
Шаг 1. Раскроем внутреннюю скобку (не трогая остальное): 7a + 2 × (5 − (3a+b)) = 7a + 2 × (5 − 3a − b).
Шаг 2. Раскроем внешнюю скобку: 7a + 2 × (5 − (3a+b)) = 7a + 2×5 − 2×3a − 2×b.
Шаг 3. Упростим выражение: 7a + 10 − 6a − 2b = a+10-2b.
Раскрытие скобок в натуральной степени
Если стоит скобка в натуральной степени (n), то чтобы раскрыть скобки, нужно найти произведение скобок, перемноженных несколько раз (n раз).
Например, в примере (a+b)2 = (a+b)×(a+b) нужно перемножить скобки (a+b) два раза, далее раскрываем скобки, где каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.
Урок 40 Бесплатно Раскрытие скобок
Ученые, открывая все новые математические законы и правила, вместе с тем, придумывали различные обозначения, символы и знаки.
Система математических знаков и символов представляет собой математический язык, который упрощает и сокращает процесс изложения информации, позволяет точнее выразить мысль и избежать неверной трактовки и ошибок.
Кроме букв алфавитов и цифр математический язык содержит огромное множество различных символов и знаков.
Одним из наиболее часто используемых символов являются скобки.
На этом уроке рассмотрим, какие основные виды скобок существуют в математике, их обозначение и применение.
Выясним, что обозначает понятие «раскрыть скобки», познакомимся с правилами раскрытия скобок и разберем примеры применения данных правил.
Скобки в математике и их предназначение
Скобки являются парными знаками (за исключением некоторых математических обозначений): обычно первая в паре скобка- открывающая, вторая- закрывающая.
Парные скобки ограничивают часть некоторого математического выражения, т.е. заключают в себе некоторую часть целой математической записи.
В математике применяют несколько видов скобок.
Чаще всего используют три вида скобок: круглые скобки ( ), квадратные скобки [ ] и фигурные скобки <>
Круглые скобки используют:
Круглые скобки используют часто в математических выражениях для указания последовательности и приоритета математических действий и логических операций или изменения принятого порядка этих действий.
Квадратные скобки в математике, например, используют для обозначения целой части числа, для определения приоритета операции (аналогично круглым скобкам), в качестве скобок «второго уровня» и др.
Фигурные скобки применяют, например, для обозначения множеств. Одинарная фигурная скобка обозначает объединение неравенств или уравнений в систему.
Используется двойная фигурная скобка, подобно круглым и квадратным скобкам, для разграничения приоритета действий в математических выражениях, в качестве скобок «третьего уровня» и др.
Вспомним порядок выполнения действий в выражениях со скобками.
По правилу, в выражении, содержащем скобки, первыми выполняются действия, стоящие в скобках, далее по порядку умножение и деление, а затем сложение и вычитание.
На примере рассмотрим использование скобок для указания порядка действий или изменении этого порядка.
Пример:
Дано выражение \(\mathbf<8 + 5 \cdot 2>\)
Найдем значение этого выражения, используя правило, которое определяет порядок выполнения действий в математических выражениях.
Ответ: 18
Если выражение будет содержать все те же числа и математические операции, но будет записано в виде: \(\mathbf<(8 + 5)\cdot 2>\), то в первую очередь выполняется действие в скобках, а затем умножение, получим
Ответ: 26
Мы можем заметить, что при изменении порядка действий с помощью скобок изменилось значение выражения.
Существуют выражения, которые содержат несколько пар скобок. В этом случае действия выполняют, начиная с первой скобки, и далее по порядку слева направо в следующих скобках, затем все действия согласно известным правилам, определяющим порядок выполнения математических операций в выражениях.
Пример:
Первым делом выполняются действия в скобках, затем умножение, далее сложение.
Решение будет выглядеть так:
Иногда встречаются выражения, где применяются сложные сочетания скобок (вложенные скобки).
Выполнять действия следует с внутренних скобок, затем математические операции проводят, продвигаясь ко внешним скобкам.
Пример:
Решение будет выглядеть так:
Ответ: 46
Для того, чтобы проще было различить одну пару скобок от другой, скобки обозначают разными размерами, либо дополнительно применяют квадратные и фигурные скобки, либо скобки изображают попарно разным цветом.
1. Скобки обозначены разных размеров:
2. Дополнительно применены квадратные и фигурные скобки:
3. Скобки изображены попарно разным цветом:
У меня есть дополнительная информация к этой части урока!
Скобки в качестве символа математического языка стали использовать в XVI— начале XVII века.
Первыми появились скобки [ ] в 1550 г. их ввел итальянский математик Рафаэль Бомбелли.
Круглые скобки ( ) появились в 1556 г.
Итальянский математик Никколо Тарталье впервые применил круглые скобки в написанной им в 1556 г.,книге под названием «Общие исследования чисел и мер».
Фигурные скобки появились немного позже, в 1593 году, благодаря французскому математику Франсуа Виету.
Несмотря на появление скобок различных видов, долгое время многие ученые, математики предпочитали вместо скобок подчеркивать выделяемое выражение или изображать линию над выделяемым выражением.
Широкое распространение скобки получили позже (в первой половине XVIII века), благодаря математикам Г. В. Лейбницу и Л. Эйлеру
Пройти тест и получить оценку можно после входа или регистрации
Раскрытие скобок
Как вам уже известно, скобки в математических выражениях часто используют для разграничения рядом стоящих знаков или для объединения и перегруппировки чисел, с которыми будут выполнятся определенные математические действия.
Но иногда при решении математических выражений удобно раскрыть скобки, нежели высчитывать их значение.
Раскрыть скобки- это значит освободить выражение от скобок, избавить выражение от лишних знаков, тем самым упростить его для вычисления.
Значение выражение со скобками и значение выражения, полученное после раскрытия скобок, равны, их записывают в виде равенства.
При преобразовании громоздких выражений, в которых содержится большое количество скобок, возникает потребность записывать промежуточные результаты вычислений. В таких случаях решение записывается в виде цепочки равенств.
Рассмотрим правила раскрытия скобок.
Разберем случаи, когда перед скобками стоит знак плюс «+».
1. Выражение вида а + (-b) можно записать, опустив скобки.
2. Выражение вида а + (b+ c) можно записать без скобок.
Согласно сочетательному свойству сложения, если к числу прибавить сумму двух чисел, то нужно сначала к этому числу прибавить первое слагаемое, а затем второе слагаемое.
а + (b + c) = а + b + c
3. Рассмотрим еще одно выражение а + (b— c), и преобразуем это выражение в выражение без скобок.
Если первое слагаемое в скобках стоит без знака, то его знак определяется как знак плюс «+».
Известно, что вычитание можно заменить сложением, следовательно:
а + (b— c) = а + (b+ (-c))
Применив сочетательное свойство, упростим выражение а + (b+ (-c)), в результате получим:
а + (b — c) = а + b — c
Рассуждая подобным образом, попробуем преобразовать еще два выражения со скобками.
4. Преобразуем выражение вида а + (-b+ c) в выражение без скобок.
Зная, что вычитание можно заменить сложением и применив сочетательное свойство сложения, упростим выражение:
5. Преобразуем выражение вида а + (-b— c) в выражение без скобок.
Зная, что вычитание можно заменить сложением, и применив сочетательное свойство сложения, упростим выражение:
Заметим, что в левой части каждого из равенств перед скобкой стоит знак «+», а слагаемые, стоящие в скобке, после преобразования сохраняют свои знаки:
а + (b + c) = а + b+ c
Пример: 15 + (5 + 2) = 15 + 5 + 2 = 22
а + (b — c) = а + b— c
Сформулируем правило раскрытия скобок, перед которыми стоит знак плюс:
Если перед скобками стоит знак плюс или не стоит никакого знака, то этот знак «+» и скобки необходимо опустить, сохранив знаки слагаемых, которые стояли в скобках.
Пример:
Избавимся от скобок, используя правило раскрытия скобок, перед которыми стоит знак «+».
Затем найдем значение выражения, используя переместительное свойство сложения и правило сложения чисел с разными знаками.
Ответ: 2
Рассмотрим случаи, когда перед раскрываемыми скобками стоит знак минус «-».
Вспомним, какие числа называют противоположными: два числа называют противоположными, если они отличны друг от друга только знаками, модули их равны.
Число а противоположно числу (-а).
-(-а) противоположно числу (-а).
Тогда верно утверждение, что -(-а) = а
Найдем значение выражения: -(-8 + 4)
Определим значение данного выражения двумя способами:
1. Найдем значение суммы в скобках, затем полученную сумму запишем со знаком минус «-».
В первом и во втором случае получили одинаковый результат, он равен четырем.
Сформулируем правило раскрытия скобок, перед которыми стоит знак минус.
Если перед скобками стоит знак минус, то этот знак «-» и скобки необходимо опустить, изменив знаки слагаемых, которые стояли в скобках на противоположные (знак минус меняется на плюс, знак плюс на минус).
Рассмотрим несколько равенств и раскроем скобки в них согласно данному правилу.
У меня есть дополнительная информация к этой части урока!
В математике существуют правила достаточно объемные и сложные для понимания.
Благодаря стихотворной форме некоторые математические законы, правила и формулы становятся проще для запоминания и усвоения.
В связи с этим математики придумали множество забавных стихотворений о правилах раскрытия скобок.
Вот некоторые из них:
1. Если перед скобкой минус,
Он ведет себя как вирус.
Скобки сразу все съедает,
Всем, кто в скобках, знак меняет.
Ну, а если плюс стоит,
Он все знаки сохранит.
2. Перед скобкой плюс стоит,
Он о том и говорит,
Что ты скобки опускай,
Да все числа выпускай.
Перед скобкой минус строгий
Загородит нам дорогу.
Чтобы скобки все убрать,
Надо знаки поменять.
3. Перед скобкой вижу плюс,
Ошибиться не боюсь.
Пример:
Избавимся от скобок, используя правило раскрытия скобок, перед которыми стоит знак «-».
Затем найдем значение выражения, используя переместительное свойство сложения и правило сложения чисел с разными знаками.
Разберем правило раскрытия скобок при умножении числа на сумму (суммы на число).
Правило раскрытия скобок для данного случая звучит так:
Для раскрытия скобок в выражениях, содержащих умножение суммы на число или числа на сумму, используется распределительное свойство умножения относительно сложения.
Если число с положительное, то знаки слагаемых a и b не изменяются.
Если число с отрицательное, то знаки слагаемых a и b меняются на противоположные.
Пример:
Воспользуемся правилом раскрытия скобок при умножении суммы на число.
Ответ: 3,8
Пример:
Воспользуемся правилом раскрытия скобок при умножении суммы на число.
Пройти тест и получить оценку можно после входа или регистрации
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Раскрытие скобок: правила, примеры, решения
Раскрытие скобок является одним из видов преобразования выражения. В этом разделе мы опишем правила раскрытия скобок, а также рассмотрим наиболее часто встречающиеся примеры задач.
Что называется раскрытием скобок?
Скобки используются для указания на порядок выполнения действий в числовых и буквенных выражениях, а также в выражениях с переменными. От выражения со скобками удобно перейти к тождественно равному выражению без скобок. Например, заменить выражение 2 · ( 3 + 4 ) на выражение вида 2 · 3 + 2 · 4 без скобок. Этот прием носит название раскрытия скобок.
Под раскрытием скобок подразумевают приемы избавления от скобок и рассматривают его обычно в отношении выражений, которые могут содержать:
Правила раскрытия скобок, примеры
Приступим к рассмотрению правил раскрытия скобок.
У одиночных чисел в скобках
Положительные числа обычно записываются без использования скобок, так как скобки в этом случае излишни.
Следует понимать, что записать выражение 3 · ( − 5 ) как 3 · − 5 нельзя. Об этом речь пойдет в следующих пунктах.
Давайте посмотрим, на чем основываются правила раскрытия скобок.
Под a и b можно понимать не только числа, но также произвольные числовые или буквенные выражения со знаком « + » впереди, которые не являются суммами или разностями. Во всех этих случаях можно применять правила точно также, как мы делали это в отношении одиночных чисел в скобках.
В произведениях двух чисел
Начнем с правила раскрытия скобок в произведении двух чисел.
Верность первой части записанного правила подтверждается правилом умножения отрицательных чисел. Для подтверждения второй части правила мы можем использовать правила умножения чисел с разными знаками.
Рассмотрим несколько примеров.
На месте отрицательных чисел − a и − b могут быть любые выражения со знаком минус впереди, которые не являются суммами или разностями. К примеру, это могут быть произведения, частные, дроби, степени, корни, логарифмы, тригонометрические функции и т.п.
Правило может быть использовано для выполнения умножения и деления выражений с разными знаками. Приведем два примера.
В произведениях трех и большего количества чисел
Перейдем к произведенимя и частным, которые содержат большее количество чисел. Для раскрытия скобок здесь будет действовать следующее правило. При четном количестве отрицательных чисел можно опустить скобки, заменив числа противоположными. После этого необходимо заключить полученное выражение в новые скобки. При нечетном количестве отрицательных чисел, опустив скобки, заменить числа на противоположные. После этого полученное выражение необходимо взять в новые скобки и поставить перед ним знак минус.
Приведенное выше правило может быть использовано при раскрытии скобок в выражениях, которые представляют собой произведения и частные со знаком минус, не являющихся суммами или разностями. Возьмем для примера выражение
Раскрытие скобок, перед которыми стоит знак «+»
Рассмотрим правило, которое можно применить для раскрытия скобок, перед которыми стоит знак плюс, а «содержимое» этих скобок не умножается и не делится на какое-либо число или выражение.
Согласно правилу скобки вместе со стоящим перед ними знаком опускаются, при этом знаки всех слагаемых в скобках сохраняются. Если перед первым слагаемым в скобках не стоит никакого знака, то нужно поставить знак плюс.
Вот еще один пример раскрытия скобок:
Как раскрываются скобки, перед которыми стоит знак минус
Выражения с переменными могут быть преобразованы с использованием того же правила:
Раскрытие скобок при умножении числа на скобку, выражения на скобку
Умножение скобки на скобку
Благодаря ряду несложных приемов мы можем прийти к сумме произведений каждого из слагаемых из первой скобки на каждое из слагаемых из второй скобки. Правило можно распространить на любое количество слагаемых внутри скобок.
Сформулируем правила умножения скобки на скобку: чтобы перемножить между собой две суммы, необходимо каждое из слагаемых первой суммы перемножить на каждое из слагаемых второй суммы и сложить полученные результаты.
Формула будет иметь вид:
Проведем раскрытие скобок в выражении ( 1 + x ) · ( x 2 + x + 6 ) Оно представляет собой произведение двух сумм. Запишем решение: ( 1 + x ) · ( x 2 + x + 6 ) = = ( 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6 ) = = 1 · x 2 + 1 · x + 1 · 6 + x · x 2 + x · x + x · 6
Раскрытие скобок в произведениях нескольких скобок и выражений
Скобка в натуральной степени
Степени, основаниями которых являются некоторые выражения, записанные в скобках, с натуральными показателями можно рассматривать как произведение нескольких скобок. При этом по правилам из двух предыдущих пунктов их можно записать без этих скобок.
Разберем еще один пример:
1 x + 2 3 = 1 x + 2 · 1 x + 2 · 1 x + 2 = = 1 x · 1 x + 1 x · 2 + 2 · 1 x + 2 · 2 · 1 x + 2 = = 1 x · 1 x · 1 x + 1 x · 2 · 1 x + 2 · 1 x · 1 x + 2 · 2 · 1 x + 1 x · 1 x · 2 + + 1 x 2 · 2 + 2 · 1 x · 2 + 2 · 2 · 2
Деление скобки на число и скобки на скобку
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Вот еще один пример деления на скобку:
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида, т.е. в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок выполнения действий:
Имея дело с выражениями, которые содержат скобки в скобках, удобно проводить преобразования, продвигаясь изнутри наружу.
Раскрытие скобок
Понятие раскрытия скобок
В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.
Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.
Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:
Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.
Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.
В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:
Раскрытие скобок также можно рассматривать шире.
Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:
Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:
Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.
Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:
Первое правило раскрытия скобок
Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.
Первое правило раскрытия скобок
Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.
Формула раскрытия скобок
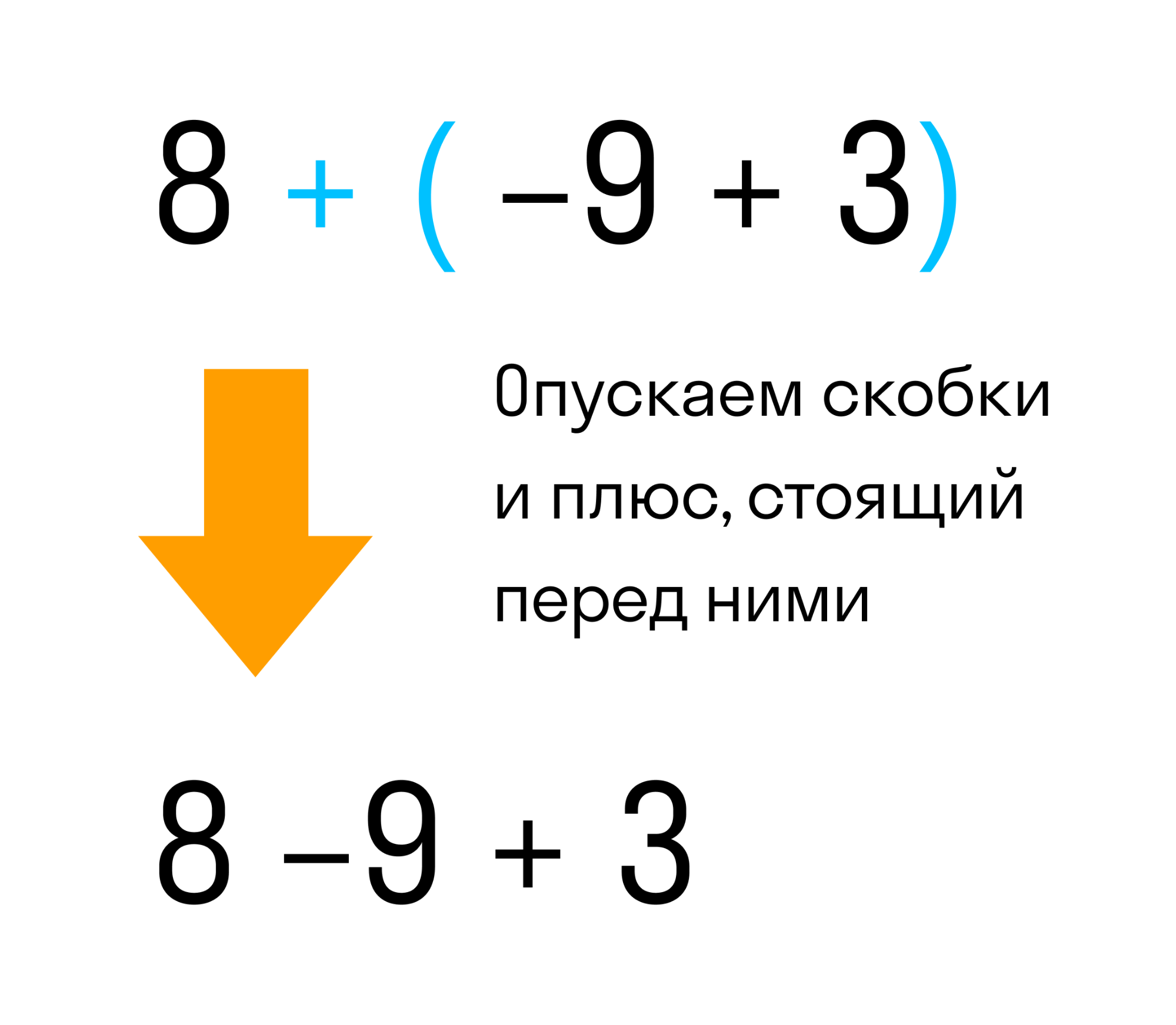
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:
Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.
Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:
Потренируемся применять правило на примерах.
Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)
Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:
Пример 2. Раскрыть скобки в выражении 6 + (−2)
Перед скобками стоит плюс, значит применим то же правило:
Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.
В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.
Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.
Идем дальше. Теперь упростим выражение 2a + a − 5b + b.
Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:
Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.
Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.
После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:
Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:
Пример 3. Раскрыть скобки 6 + (−3) + (−2)
В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:
Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.
Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.
Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:
Пример 4. Раскрыть скобки в выражении (−7)
Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:
Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)
Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:
Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!
Второе правило раскрытия скобок
Здесь рассмотрим второе правило раскрытия скобок. Звучит так:
Второе правило раскрытия скобок
Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.
Формула раскрытия скобок
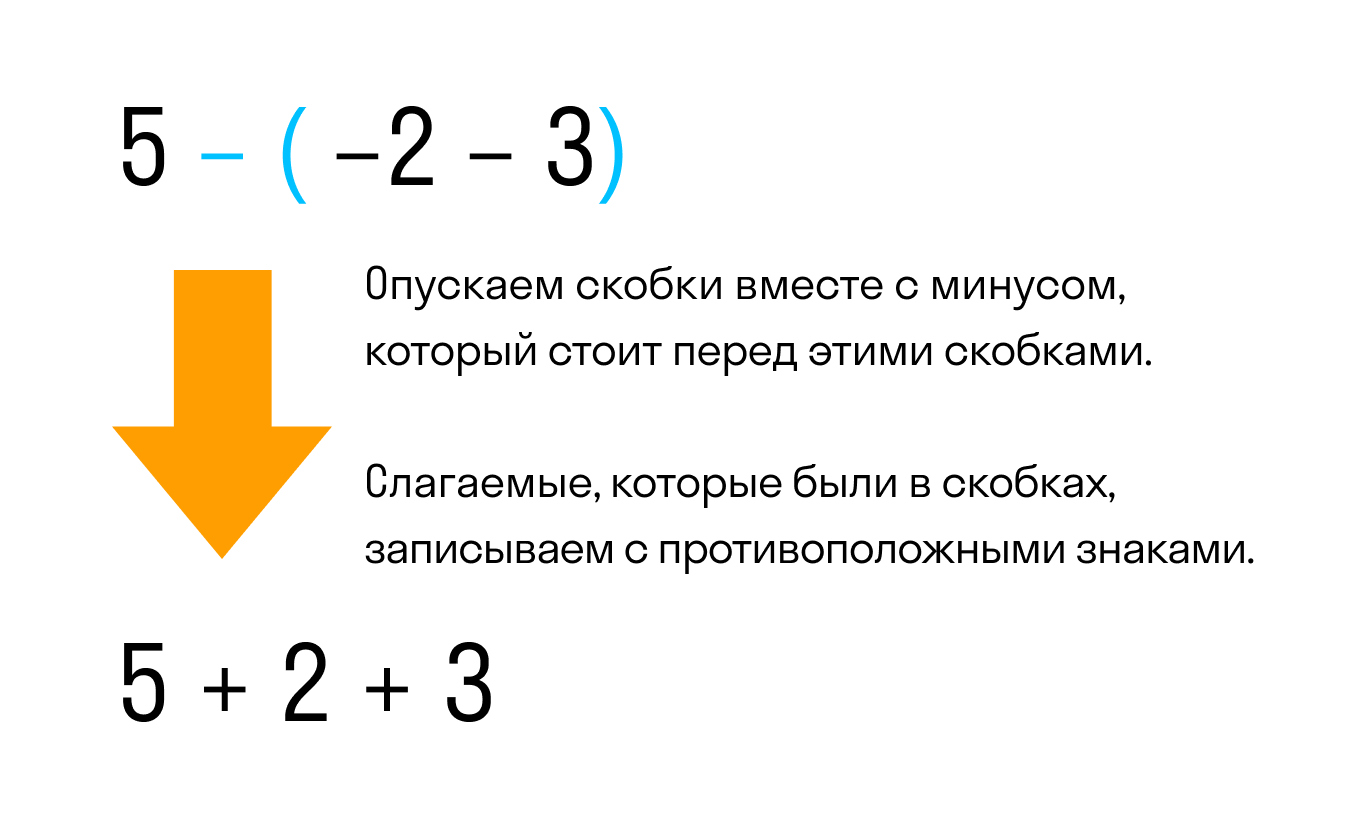
Например, раскроем скобки в выражении 5 − (−2 − 3)
Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:
Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.
Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:
Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
18 − (−1 − 5) = 18 + 1 + 5
Пример 2. Раскрыть скобки −(−6 + 7)
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)
Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:
−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2
Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10
Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:
a − (3b + 3) + 10 = a − 3b − 3 + 10
Другие правила раскрытия скобок
Правило раскрытия скобок при делении
Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.
Формула раскрытия скобок
Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.
Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.
Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:
Далее умножим скобку на число:
Правило раскрытия скобок при умножении:
Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.
Формула раскрытия скобок
Пример 1. Раскрыть скобки 5(3 − x)
В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:
Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.
Пример 2. Упростить выражение: 5(x + y) − 2(x − y)
Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.
Таблица с формулами раскрытия скобок
Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.
Правила раскрытия круглых скобок вида (-a), в которых находится одночлен
Правила раскрытия круглых скобок, в которых находится многочлен
Скобки убирают, знаки всех слагаемых в скобках не меняют, если:
Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:
Раскрытие круглых скобок при умножении одночлена на многочлен
Раскрытие круглых скобок при умножении многочлена на многочлен
Раскрытие круглых скобок при возведении многочлена в степень
(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2
Скобка в скобке
В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:
Чтобы успешно решать подобные задания, нужно:
При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.
Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))
Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.
Теперь раскроем вторую скобку, внешнюю:
Упростим получившееся выражение:
Порядок раскрытия скобок
Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.
Порядок раскрытия скобок согласован с порядком выполнения действий:
Пример 1. Раскрыть скобки и упростить выражение:
Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.
Задачи для самостоятельного решения
На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.
Задание 6. Раскройте скобки:
Задание 7. Раскройте скобки: