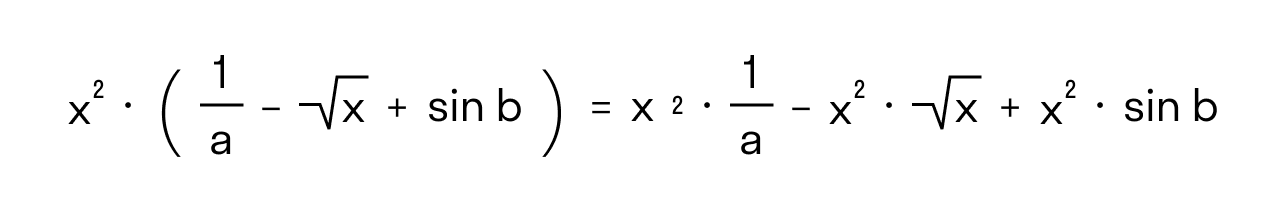Что значит раскрыть скобки по русскому языку

Раскрытие скобок: правила и примеры

Раскрытие скобок и правила применения — это одна из основных тем математике, на базе которой решаются многие задания во всех последующих классах. Поэтому правила раскрытия скобок необходимо усвоить в обязательном порядке.

Раскрытие скобок: правила

Правило раскрытия скобок при сложении

Если перед скобками стоит плюс, то скобки просто опускаются.
Иными словами, скобки исчезнут, а то, что было в скобках, запишется без изменений.
Например, (a−b) = a−b.

В данном правиле следует учитывать, что в математике не принято писать знак плюс, если он стоит в выражении первым. Например, если мы складываем два положительных числа 2 и 3, то запишем 2+3, а не +2+3. Значит перед скобками, которые стоят в начале выражения, стоит плюс, который не пишут.

Пример 1: 8+(5−3) = 10. Ответ: 8+5–3 = 10.
Пример 2: 6+(−1+2) = 7. Ответ: 6–1+2 = 7.
Пример 3: 8a + (3b −6a). Ответ: 8a + 3b −6a = 2a + 3b.

Правило раскрытия скобок при вычитании

Если перед скобками стоит минус, то скобки опускаются, а каждое слагаемое внутри нее меняет свой знак на противоположный.
Например, −(a−b) = −a+b

Пример 1: 8–(5–3) = 6. Ответ: 8 – 5 + 3 = 6.
Пример 2: 6 − (−1 + 2) = 5. Ответ: 6 + 1 – 2 = 5.
Пример 3: 8a–(3b −6a). Ответ: 8a – 3b + 6a = 14a – 3b.
Пример 4: −(5b −2). Ответ: −5b +2.

Раскрытие скобок при умножении

Если перед скобками стоит знак умножения, то каждое число внутри скобок умножается на множитель, стоящий перед скобками.
При этом умножение минуса на минус дает плюс, а умножение минуса на плюс дает минус.
Данное правило основано на распределительном законе умножения: a(b+c) = ab + ac.

Пример 1: 8×(5 − 3) = 16. Ответ: 8 ×5 − 8 ×3 = 16.
Пример 2: a×(7 +2). Ответ: a×7+a×2 = 7a + 2a = 9a.
Пример 3: 8×(3b −6a). Ответ: 8×3b – 8×6a = 24b–48a

Раскрытие скобок при делении

Если после скобок стоит знак деления, то каждое число, стоящее внутри скобок, делится на делитель, стоящий после скобок.

Пример 1: (25−15):5. Ответ: 25:5−15:5= 2.
Пример 2: (−14a +10):2. Ответ: −14a:2 +10:2 = −7a +5.
Пример 3: (36b + 6a):6. Ответ: 36b:6 + 6a:6 = 6b + a.

Раскрытие скобок при умножении двух скобок

При умножении скобки на скобку, каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.
Например, (c+d) × (a−b) = c×(a−b)+d×(a−b) = ca−cb+da−db

Пример. Раскрыть скобки: (2−a) × (3a−1).
Решение:
Шаг 1. Убираем первую скобку (каждое ее слагаемое умножаем на вторую скобку): 2 × (3a−1) − a × (3a−1).
Шаг 2. Раскрываем произведение скобок: (2×3a− 2×1) – (a×3a−a×1) = 2×3a− 2×1 – a×3a + a×1.
Шаг 3. Перемножаем и приводим подобные слагаемые: 6a–2–3a2+a = 7a–2–3a2

Раскрытие вложенных скобок

Иногда встречаются примеры со скобками, которые вложены в другие скобки. Чтобы решить такую задачу, нужно сначала раскрыть внутреннюю скобку (при этом остальное выражение оставить без изменений), а потом внешнюю скобку.

Пример 1. 7a + 2 × (5− (3a+b)).
Решение:
Шаг 1. Раскроем внутреннюю скобку (не трогая остальное): 7a + 2 × (5 − (3a+b)) = 7a + 2 × (5 − 3a − b).
Шаг 2. Раскроем внешнюю скобку: 7a + 2 × (5 − (3a+b)) = 7a + 2×5 − 2×3a − 2×b.
Шаг 3. Упростим выражение: 7a + 10 − 6a − 2b = a+10-2b.

Раскрытие скобок в натуральной степени

Если стоит скобка в натуральной степени (n), то чтобы раскрыть скобки, нужно найти произведение скобок, перемноженных несколько раз (n раз).

Например, в примере (a+b)2 = (a+b)×(a+b) нужно перемножить скобки (a+b) два раза, далее раскрываем скобки, где каждое слагаемое первой скобки умножается на каждое слагаемое второй скобки.

Источник

Про скобки в русском языке

Рассмотрим правила употребления круглых и квадратных скобок в русском языке.

Скобки являются двойным знаком препинания, в который заключаются поясняющие или дополняющие высказываемую мысль слова и предложения. Первая скобка — открывающая, вторая — закрывающая. В русском языке чаще всего используют круглые ( ) и квадратные скобки [ ]. На правилах их употребления мы подробно и остановимся в этой статье.

Круглые скобки

Круглые скобки в русском языке используются для выделения пояснительных, уточняющих, дополняющих конструкций. Так, в скобках может заключаться уточнение значения отдельного слова, даваться попутное указание для разъяснения смысла фразы, указываться авторское замечание, дополнение высказываемой мысли. Такими вставными конструкциями могут быть как отдельные слова, так и целые предложения, и находиться они могут в середине или в конце предложения. По тому, насколько верно копирайтер использует типографские знаки в тексте, к которым относятся скобки (а также тире, кавычки, многоточие), можно судить об уровне его профессионализма.
Рассмотрим основные значения вставных конструкций и примеры их использования:

1) Дополнение содержания высказывания. Например:

В один прекрасный день (это было в прошлом году) мне позвонил с работы муж.

В 1976 году я наконец получила диплом по бухгалтерскому делу (я с отличием закончила Флоридский университет) и мечта моих родителей осуществилась.

2) Пояснение или уточнение части высказывания или отдельных слов. Например:

Орегано отлично дополняет блюда из мяса (особенно баранину).

Цезарь (так звали льва в зверинце) спит и тихо взвизгивает во сне.

Село Новосельское (мы говорим о Новокубанском районе) расположено среди распаханных полей.

3) Пояснение мысли высказывания в целом. Например:

Я заплатил наличными пять тысяч за дом, стоивший мне сорок пять тысяч (на самом деле его цена была шестьдесят пять, но никто не хотел его покупать).

4) Добавочное авторское замечание, восклицание или вопрос. Например:

Охотники (а их немало в этом краю) чувствуют себя гостями в лесу (В. Тендряков).

Время (дело известное) летит иногда птицей, иногда ползет червяком; но человеку бывает особенно хорошо тогда, когда он даже не замечает – скоро ли, тихо ли оно проходит (И. Тургенев).

Однажды, проснувшись ночью в своем доме в пригороде по уши в долгах (воплощение американской мечты), они говорят себе: «Мои финансовые проблемы можно решить, если найти способ быстро разбогатеть» (Р. Кийосаки).

Помимо этого, круглые скобки используются:

1) Для ремарок в стенограммах речей, выступлений, докладов, обращений. При этом перед закрывающей скобкой в конце ремарки ставится точка, а точка и вопросительный/восклицательный знак перед открывающей скобкой сохраняются. Например:

На этом мой доклад заканчивается. Уверен, человечество сможет преодолеть эти трудности! (Все встают. Аплодисменты.)

Печать издания откладывается. (Редакция.)

2) Для ремарок в драматическом тексте. Например:

Я только поклонюсь вам и тотчас же уйду. (Горячо целует руку.) Мне приказано было ждать до утра, но у меня не хватило терпения.

3) Для указания источника цитирования или имени автора и названия произведения, из которого взята цитата. Например:

«Вы все отрицаете, или, выражаясь точнее, вы все разрушаете… Да ведь надобно же и строить. » (И. С. Тургенев. Отцы и дети). Заглавие источника отделяется точкой от фамилии автора и не заключается в кавычки.

«Знаки препинания — это как нотные знаки. Они твёрдо держат текст и не дают ему рассыпаться» (К. Г. Паустовский).

4) В маркированных списках может использоваться закрывающая круглая скобка. Например:
1); а).

Знаки препинания до скобок

По правилам русского языка, перед открывающей и закрывающей скобкой знаки препинания не ставятся. Это относится к запятой, точке с запятой, тире, двоеточию. Постановка данных пунктуационных знаков возможна только после закрывающей скобки. Например:

Вся эта стройка (как позже выяснилось) — дедушкина затея.

Перед закрывающей скобкой могут стоять вопросительный или восклицательный знак, многоточие, точка. Например:

Сегодня отличная погода (наконец-то дождя нет!)

Между тем лесок (какой там лесок — осиновые кустики!) начал смутно проступать.

Знаки препинания после скобок

После закрывающей скобки ставится такой знак препинания, который необходим по условиям предложения, при этом не имеет значения, какой знак находится до закрывающей скобки (вопросительный, восклицательный, многоточие или точка). Например:

Неверие — в греческом языке означает не только «недоверчивость» (что мы называем скепсисом, когда, например, говорим об атеизме), но и нежелание соблюдать договоренности хотя бы и устные.

Квадратные скобки в русском языке

Квадратные скобки в предложении ставятся при цитировании. В них заключают текст автора, который призван прояснить контекст цитаты. Например:

«Их [детей] было семеро».

Также квадратные скобки применяются при оформлении библиографических списков.

Как поставить квадратные [скобки] на клавиатуре

Символы квадратных скобок находятся на буквенной клавиатуре. Открывающая скобка расположена на русской букве «Х», а закрывающая — на букве «Ъ». Поставить квадратные скобки очень легко: нужно в английской раскладке нажать на клавиши с соответствующим обозначением.

Источник

Раскрытие скобок

Понятие раскрытия скобок

В задачах по математике постоянно встречаются числовые и буквенные выражения, а также выражения с переменными, которые составлены с использованием скобок.

Основная функция скобок — менять порядок действий при вычислениях значений числовых выражений.

Часто можно перейти от одного выражения со скобками к тождественно равному выражению без скобок. Например:

Такой переход от выражения со скобками к тождественно равному выражению без скобок несет в себе основную идею о раскрытии скобок.

Начальное выражение со скобками и результат, полученный после раскрытия скобок, удобно записывать в виде равенства, как мы это сделали в предыдущем примере.

В школе тему раскрытия скобок обычно подходят в 6 классе. На этом этапе раскрытие скобок воспринимают, как избавление от скобок, которые указывают порядок выполнения действий. И изучают раскрытие скобок на примерах выражений, которые содержат:

Раскрытие скобок также можно рассматривать шире.

Раскрытием скобок можно назвать переход от выражения, которое содержит отрицательные числа в скобках, к выражению без скобок. Например:

Или, если в описанных выше выражениях вместо чисел и переменных могут быть любые выражения. В полученных таким способом выражениях тоже можно проводить раскрытие скобок. Например:

Раскрытие скобок — это избавление от скобок, которые указывают порядок выполнения действий, а также избавление от скобок, в которые заключены отдельные числа и выражения.

Важно отметить еще один момент, который касается особенностей записи решения при раскрытии скобок. При раскрытии скобок в громоздких выражениях можно прописывать промежуточные результаты в виде цепочки равенств. Например, вот так:

Первое правило раскрытия скобок

Это выражение равно двум. А теперь раскроем скобки, то есть избавимся от них. Мы ожидаем, что после избавления от скобок значение выражения 8 + (−9 + 3) также должно быть равно 2.

Первое правило раскрытия скобок

Если перед скобками стоит знак плюс — все числа, которые стоят внутри скобок, сохраняют свой знак.

Формула раскрытия скобок

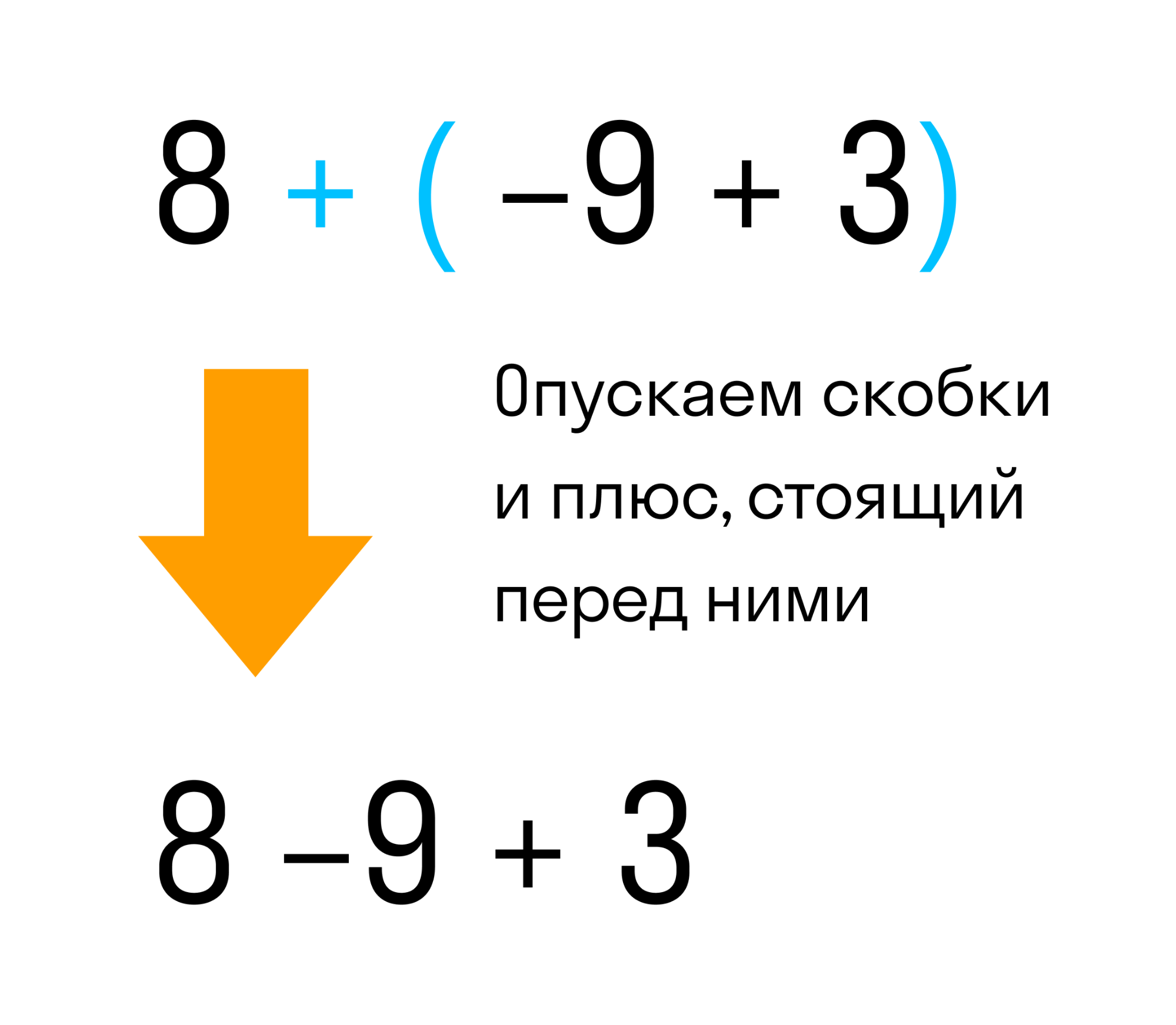
Мы видим что в выражении 8 + (−9 + 3) перед скобками стоит плюс. Значит плюс нужно опустить вместе со скобками. То, что было в скобках — запишем без изменений, вот так:

Так мы получили выражение без скобок 8 − 9 + 3. Снова получаем в результате вычисления два.

Поэтому между выражениями 8 + (−9 + 3) и 8 − 9 + 3 можно поставить знак равенства, поскольку они равны одному и тому же значению:

Потренируемся применять правило на примерах.

Пример 1. Раскрыть скобки в выражении 8 + (−3 − 1)

Перед скобками стоит плюс, значит этот плюс опустим вместе со скобками. А то, что было в скобках оставим без изменений:

Пример 2. Раскрыть скобки в выражении 6 + (−2)

Перед скобками стоит плюс, значит применим то же правило:

Раскрытие скобок в предыдущих пример выглядит, как обратная операция замены вычитания сложением.

В выражении 6 − 2 происходит вычитание, но его можно заменить сложением. Тогда получится выражение 6 + (−2). Но если в выражении 6 + (−2) раскрыть скобки, то получится снова 6 − 2.

Поэтому первое правило раскрытия скобок можно использовать для упрощения выражений после любых других преобразований.

Идем дальше. Теперь упростим выражение 2a + a − 5b + b.

Чтобы упростить такое выражение, нужно привести подобные слагаемые. Для этого нужно сложить коэффициенты подобных слагаемых и результат умножить на общую буквенную часть:

Получили выражение 3a + (−4b). Раскроем скобки. Перед скобками стоит плюс, поэтому используем первое правило раскрытия скобок: опустим скобки вместе с плюсом, который стоит перед этими скобками.

Таким образом, выражение 2a + a − 5b + b упрощается до 3a − 4b.

После открытия одних скобок, по пути можно найти другие. К ним применяем те же правила, что и к первым. Например, раскроем скобки в таком выражении:

Здесь нужно раскрыть скобки в двух местах. Снова применяем первое правило раскрытия скобок, а именно опускаем скобки вместе с плюсом, который стоит перед:

Пример 3. Раскрыть скобки 6 + (−3) + (−2)

В обоих местах перед скобками стоит плюс. Применяем первое правило раскрытия скобок:

Можно встретить такой пример, когда первое слагаемое в скобках записано без знака. Например, в выражении 1 + (2 + 3 − 4) первое слагаемое в скобках 2 записано без знака. Какой знак будет стоять перед двойкой после того, как скобки и плюс, стоящий перед скобками опустятся? Ответ интуитивно понятен — перед двойкой будет стоять плюс.

Дело в том, что даже в скобках перед двойкой стоит плюс, просто мы его не видим так как плюс не принято записывать. Полная запись положительных чисел выглядит так: +1, +2, +3, но плюсы по традиции не записывают, поэтому положительные числа мы всегда видим в таком виде: 1, 2, 3.

Поэтому, чтобы раскрыть скобки в выражении 1 + (2 + 3 − 4), нужно как обычно опустить скобки вместе с плюсом, который стоит перед этими скобками, но первое слагаемое которое было в скобках записать со знаком плюс:

Пример 4. Раскрыть скобки в выражении (−7)

Перед скобками стоит плюс, но мы его не видим так как до него нет других чисел или выражений. Убираем скобки, применив первое правило раскрытия скобок:

Пример 5. Раскрыть скобки 9a + (−5b + 6c) + 2a + (−2d)

Видим два места, где нужно раскрыть скобки. В обоих участках перед скобками стоит плюс, значит этот плюс опускается вместе со скобками. То, что было в скобках запишем без изменений:

Нужно быстро привести знания в порядок перед экзаменом? Записывайтесь на курсы ЕГЭ по математике в Skysmart!

Второе правило раскрытия скобок

Здесь рассмотрим второе правило раскрытия скобок. Звучит так:

Второе правило раскрытия скобок

Если перед скобками стоит знак минус — все числа, которые стоят внутри скобок, меняют свой знак на противоположный.

Формула раскрытия скобок

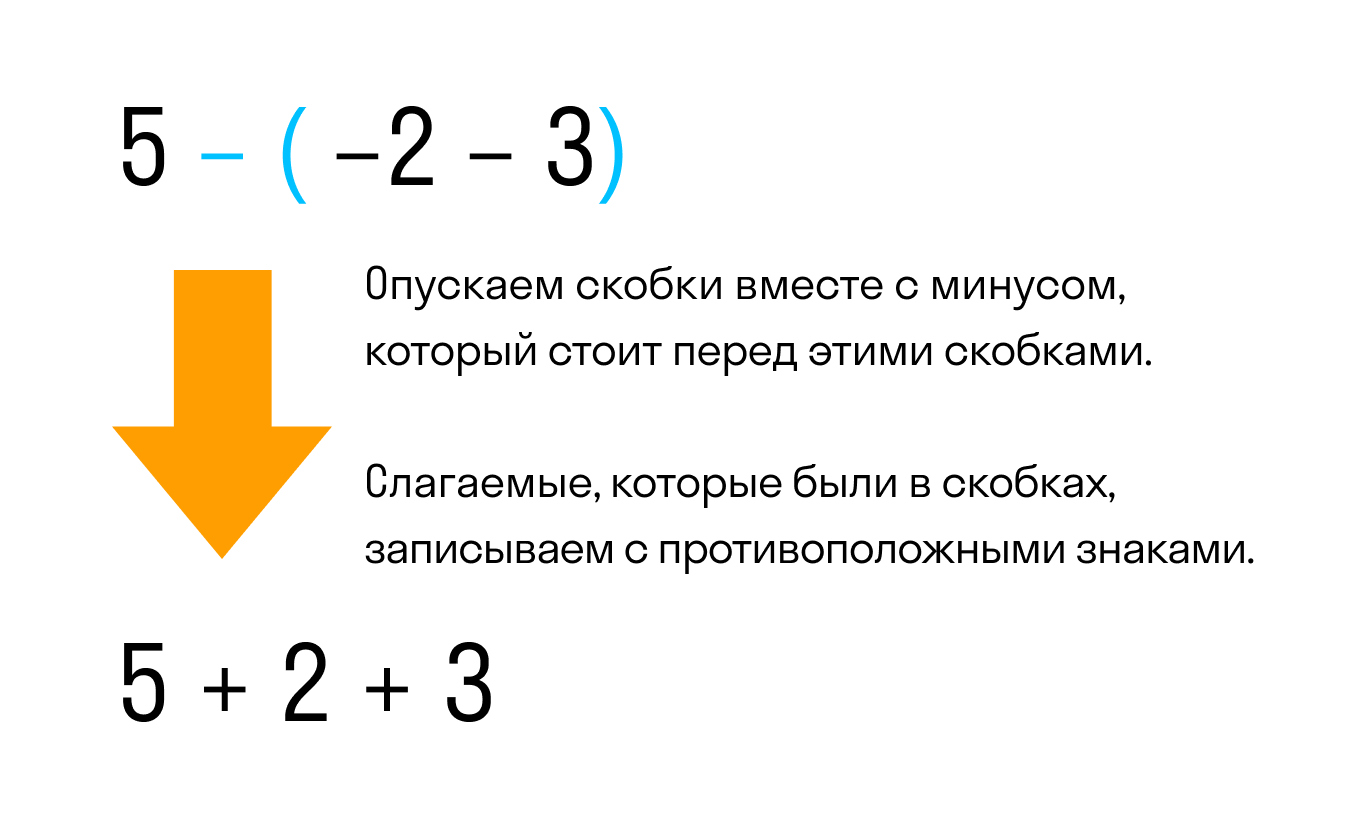
Например, раскроем скобки в выражении 5 − (−2 − 3)

Видим, что перед скобками стоит минус. Значит нужно применить второе правило раскрытия, а именно опустить скобки вместе с минусом, который стоит перед этими скобками. При этом слагаемые, которые были в скобках, поменяют свой знак на противоположный:

Так мы получили выражение без скобок 5 + 2 + 3. Это выражение равно десяти, как и предыдущее выражение со скобками было равно 10.

Поэтому между выражениями 5 − (−2 − 3) и 5 + 2 + 3 можно поставить знак равенства так как они равны одному и тому же значению:

Пример 1. Раскрыть скобки в выражении 18 − (−1 − 5)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

18 − (−1 − 5) = 18 + 1 + 5

Пример 2. Раскрыть скобки −(−6 + 7)

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

Пример 3. Раскрыть скобки −(−7 − 4) + 15 + (−6 − 2)

Здесь мы видим два места, где нужно раскрыть скобки. В первом случае применим второе правило раскрытия скобок, а во втором — первое правило:

−(−7 − 4) + 15 + (−6 − 2) = 7 + 4 + 15 − 6 − 2

Пример 4. Раскрыть скобки в выражении a − (3b + 3) + 10

Перед скобками стоит минус, поэтому применим второе правило раскрытия скобок:

a − (3b + 3) + 10 = a − 3b − 3 + 10

Другие правила раскрытия скобок

Правило раскрытия скобок при делении

Если после скобок стоит знак деления — каждое число внутри скобок делится на делитель, который стоит после скобок.

Формула раскрытия скобок

Деление скобки на число предполагает, что необходимо разделить на число все заключенные в скобки слагаемые.

Деление можно предварительно заменить умножением, после чего можно воспользоваться подходящим правилом раскрытия скобок в произведении. Это же правило применимо и при делении скобки на скобку.

Например, нам необходимо раскрыть скобки в выражении (x + 2) : 2/3. Для этого сначала заменим деление умножением на обратное число:

Далее умножим скобку на число:

Правило раскрытия скобок при умножении:

Если перед скобками стоит знак умножения — каждое число, которое стоит внутри скобок, нужно умножить на множитель перед скобками.

Формула раскрытия скобок

Пример 1. Раскрыть скобки 5(3 − x)

В скобке у нас стоят 3 и −x, а перед скобкой — пятерка. Значит, каждый член скобки нужно умножить на 5:

Знак умножения между числом и скобкой в математике не пишут для сокращения размеров записей.

Пример 2. Упростить выражение: 5(x + y) − 2(x − y)

Как решаем: 5(x + y) − 2(x − y) = 5x + 5y − 2x + 2y = 3x + 7y.

Таблица с формулами раскрытия скобок

Эти таблицы с правилами раскрытия скобок можно распечатать и обращаться к ним, когда возникнут сомнения в ходе решения задачки.

Правила раскрытия круглых скобок вида (-a), в которых находится одночлен

Правила раскрытия круглых скобок, в которых находится многочлен

Скобки убирают, знаки всех слагаемых в скобках не меняют, если:

Скобки убирают, знаки всех слагаемых в скобках меняются на противоположные, если:

Раскрытие круглых скобок при умножении одночлена на многочлен

Раскрытие круглых скобок при умножении многочлена на многочлен

Раскрытие круглых скобок при возведении многочлена в степень

(a + b)2 = (a + b)(a + b) = a(a + b) + b(a + b)= a2 + ab + ab + b2 = a2 + 2ab + b2

Скобка в скобке

В 7 классе на алгебре можно встретить задачи со скобками, которые вложены внутрь других скобок. Вот пример такого задания:

Чтобы успешно решать подобные задания, нужно:

При этом важно при раскрытии одной из скобок не трогать все остальное выражение и просто переписывать его, как есть. Разберем подробнее тот же самый пример.

Пример 1. Раскрыть скобки и привести подобные слагаемые 7x + 2(5 − (3x + y))

Начнем с раскрытия внутренней скобки (той, что внутри). Раскрывая ее, имеем дело только с тем, что к ней непосредственно относится – это сама скобка и минус перед ней. Всё остальное переписываем также как было.

Теперь раскроем вторую скобку, внешнюю:

Упростим получившееся выражение:

Порядок раскрытия скобок

Теперь рассмотрим порядок применения правил, разобранных выше в выражениях общего вида. То есть в выражениях, которые содержат суммы с разностями, произведения с частными, скобки в натуральной степени.

Порядок раскрытия скобок согласован с порядком выполнения действий:

Пример 1. Раскрыть скобки и упростить выражение:

Значение выражения не зависит от переменной и всегда отрицательно. Что и требовалось доказать.

Задачи для самостоятельного решения

На алгебре в 6 и 7 классе придется решать задачки с раскрытием скобок много и часто. Поэтому лучше запомнить правила и практиковаться уже сейчас.

Задание 6. Раскройте скобки:

Задание 7. Раскройте скобки:

Источник

Как и когда ставить текст в скобках. Правила русского языка

Скобки – парный знак препинания, который выполняет выделительную функцию. Различают круглые, квадратные, фигурные и угловые скобки. Копирайтеры в своей работе чаще всего ставят круглые скобки. Рассмотрим более подробно варианты использования скобок в тексте.

Вставные конструкции со скобками

Круглые скобки необходимы, если в предложении содержатся вставные конструкции. Такие конструкции могут находиться только в середине или в конце предложения и обычно заключаются в скобки. Этот знак препинания является рекомендованным, может заменяться запятыми или тире.

Скобки ставят, если надо уточнить значение отдельных слов, дать попутное указание, разъясняющее смысл фразы, или вставить замечание, дополняющее высказывание. Приведем примеры основных значений вставных конструкций:

Конкретизация в маркированных списках, прайс-листах: Штукатурка (выравнивание стен). Монтаж пластикового уголка (наружного, внутреннего).

Пояснение отдельных слов: Рекомендации по профилактике эмоционального выгорания предоставил Иванов И.И. (доктор медицинских наук, член-корреспондент РАН).

Пояснение основного содержания: Ключевая задача рекламы товара – максимально отличаться от конкурента (выступать как опознавательный знак) и быть узнаваемой потребителями.

Дополнение смысла высказывания: Нужна постоянная практика и знание правил копирайтинга (часть их Вы уже изучили).

Выражение эмоций автора текста: Каждый человек обязан (я подчеркиваю – обязан!) заботиться о своем физическом и психическом здоровье.

Скобки при оформлении цитат

Если требуется после цитаты указать источник цитирования или фамилию автора, то эта информация заключается в скобки. Приведем примеры.

Верховный суд указал, что «цитирование производится для иллюстрации, подтверждения или опровержения высказывания автора» (Определение ВС РФ № 78-ГОЗ-77 от 05.12.2003).

«Клиент получает ту рекламу, которую он заслуживает!» (Огилви Д. Откровения рекламного агента). Заглавие источника отделяется точкой от фамилии автора и не заключается в кавычки.

Сочетание скобок и других знаков

Важно помнить, что перед скобкой (открывающей или закрывающей) никогда не ставится знак препинания: запятая, двоеточие, точка с запятой, тире. Эти пунктуационные знаки уместны после закрывающей скобки.

Возьмите на заметку! Не используйте предложения с двойными скобками. Если внутри одной вставной конструкции надо вставить еще одну, то внешнее (первое вводное предложение) выделяется скобками, а внутреннее – при помощи тире.

Скобки редко встречаются в тексте и поэтому привлекают внимание читателей. Всегда помните, что и как ставить в скобки.

Источник