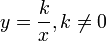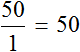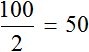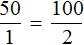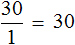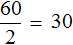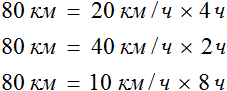Что значит прямо пропорционально простыми словами

Прямая пропорциональность

Содержание

Пример

Масса керосина пропорциональна его объёму: 2 л керосина весят 1,6 кг, 5 л весят 4 кг, 7 л весят 5,6 кг. Отношение массы к объёму всегда будет равно плотности:

1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.

Коэффициент пропорциональности

Прямая пропорциональность

Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.

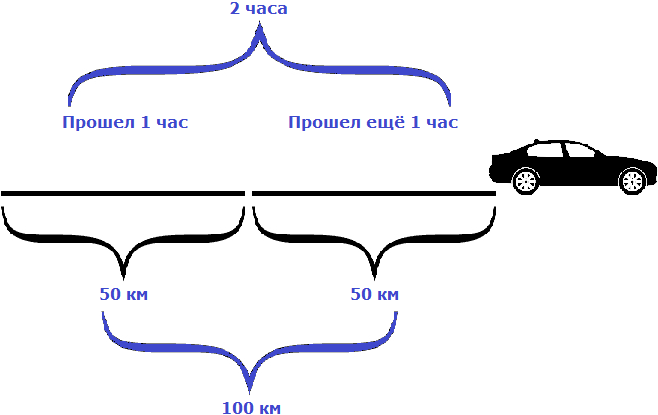
Математически прямая пропорциональность записывается в виде формулы:

Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.

Обратная пропорциональность

Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).

Математически обратная пропорциональность записывается в виде формулы:

См. также

Источники

Полезное

Смотреть что такое «Прямая пропорциональность» в других словарях:

прямая пропорциональность — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN direct ratio … Справочник технического переводчика

прямая пропорциональность — tiesioginis proporcingumas statusas T sritis fizika atitikmenys: angl. direct proportionality vok. direkte Proportionalität, f rus. прямая пропорциональность, f pranc. proportionnalité directe, f … Fizikos terminų žodynas

ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка

ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова

Пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Содержание 1 Пример 2 Коэффициент пропорциональности … Википедия

ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова

пропорциональность — и; ж. 1. к Пропорциональный (1 зн.); соразмерность. П. частей. П. телосложения. П. представительства в парламенте. 2. Матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент пропорциональности. Прямая п. (при которой с… … Энциклопедический словарь

пропорциональность — и; ж. 1) к пропорциональный 1); соразмерность. Пропорциона/льность частей. Пропорциона/льность телосложения. Пропорциона/льность представительства в парламенте. 2) матем. Зависимость между пропорционально изменяющимися величинами. Коэффициент… … Словарь многих выражений

Обратная пропорциональность — Пропорциональными называются две взаимно зависимые величины, если отношение их значений остается неизменным.[1]. Значения двух различных величин могут взаимно зависеть друг от друга. Так, площадь квадрата зависит от длины его стороны, и обратно,… … Википедия

линейная зависимость — прямая пропорциональность. множитель. см. константа … Идеографический словарь русского языка

Источник

Урок 23 Бесплатно Прямая и обратная пропорциональные зависимости

На этом уроке мы рассмотрим, что такое прямая и обратная пропорциональные зависимости, научимся оформлять и решать задачи с помощью пропорции, устанавливая пропорциональную зависимость между величинами в ней, рассмотрим примеры задач на прямую и обратную пропорциональную зависимость.

Прямая и обратная пропорциональность

Давайте сначала разберемся, что такое пропорциональность.

Зависимость величин друг от друга может быть прямой и обратной.

Отношение между величинами описываются прямой или обратной пропорциональностью.

Прямая пропорциональность выражается так: \(\mathbf\)

Обратная пропорциональность выражается так: \(\mathbf>\)

x и y величины, зависящие друг от друга.

Пример

Если постоянно значение произведения, то множители зависят друг от друга обратно пропорционально.

По формуле видно, что площадь квадрата зависит от длины (ширины) его стороны, а длина стороны (ширина) зависит от его площади.

Какова эта зависимость, сейчас и рассмотрим.

Зависимость площади прямоугольника от длины при постоянном значении ширины является прямо пропорциональной зависимостью этих величин.

Зависимость площади прямоугольника от ширины при постоянном значении длины является прямо пропорциональной зависимостью этих величин.

Пусть одна клетка равна 1 см. Рассмотрим рисунок:

Ширина прямоугольника b постоянная величина

b = 4 см

a₁ = 6 см

a₂ = 7 см

Найдем площади прямоугольников S₁ и S₂

\(\mathbf = a_ <1>\cdot b = 6 \cdot 4 = 24>\) см 2

\(\mathbf = a_ <2>\cdot b = 7 \cdot 4 = 28>\) см 2

Вывод: при увеличении стороны прямоугольника увеличилась площадь прямоугольника.

Рассмотрим другой вариант зависимости

Зависимость одной из сторон прямоугольника от второй стороны при постоянном значении площади прямоугольника является обратно пропорциональной зависимостью. Пусть одна клетка равна 1 см

Площадь прямоугольника S постоянная величина

S = 24 см 2

b₁ = 4 см

Увеличим высоту прямоугольника- сторону прямоугольника b₁ на 2 см_, получим

b₂ = 6 см

Найдем ширину прямоугольника- сторону a₂

Вывод: при увеличении одной стороны прямоугольника и постоянном значении площади, вторая сторона уменьшается.

Таким образом, мы подошли к основным понятиям пропорциональной зависимости. Чтобы было легко разобраться в несложных схемах ниже, мы дадим пояснение символам:

1) Две величины прямо пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, так же увеличивается (уменьшается) в n количество раз.

2) Две величины обратно пропорциональны друг другу, если при увеличении (уменьшении) одной величины в n количество раз, другая величина, зависящая от первой, уменьшается (увеличивается) в n количество раз.

Примеров прямой и обратной пропорциональности множество.

Однако не все величины зависят друг от друга прямо пропорционально или обратно пропорционально, встречаются и более простые и более сложные зависимости величин.

Надо понимать, что даже если какие-нибудь две величины возрастают или убывают, то между ними не обязательно существует пропорциональная зависимость.

Например, с течением времени увеличивается возраст человека и его размер ноги, но эти величины не являются пропорциональными, так как при удвоении возраста размер ноги человека не удваивается

Пройти тест и получить оценку можно после входа или регистрации

Алгоритм решение задач с прямой и обратной пропорциональной зависимостью

Алгоритм решения задач на пропорциональную зависимость состоит из нескольких основных пунктов:

— Стрелки, которые направлены в одну сторону, обозначают прямую пропорциональную зависимость величин

— Стрелки, которые направлены в разные стороны, обозначают обратную пропорциональную зависимость величин.

5. Записать пропорцию, учитывая характер пропорциональности величин

6. Составить уравнение

7. Найти неизвестный член уравнения (искомую величину)

8. Записать ответ задачи

Важно помнить, что при составлении краткой записи задачи величины с одинаковыми единицами измерения записывают друг под другом.

Если между величинами прямая пропорциональная зависимость, то пропорция составляется точно в соответствии с краткой записью задачи.

Если между величинами обратная пропорциональная зависимость, то при составлении пропорции одноименные величины меняются местами в одном любом из столбцов таблицы (логической схемы) краткой записи задачи.

Другими словами, при прямо пропорциональной зависимости отношение значений одной величины равно отношению соответствующих значений другой величины.

При обратно пропорциональной зависимости отношение значений одной величины будет равно обратному отношению соответствующих значений другой величины.

Пройти тест и получить оценку можно после входа или регистрации

Источник

Прямая и обратная пропорциональность

Пропорциональность — это взаимосвязь между двумя величинами, при которой изменение одной из них влечет за собой изменение другой во столько же раз.

Пропорциональность бывает прямой и обратной. В данном уроке мы рассмотрим каждую из них.

Прямая пропорциональность

Предположим, что автомобиль двигается со скоростью 50 км/ч. Мы помним, что скорость это расстояние, пройденное за единицу времени (1 час, 1 минуту или 1 секунду). В нашем примере автомобиль двигается со скоростью 50 км/ч, то есть за один час он будет проезжать расстояние, равное пятидесяти километрам.

Изобразим на рисунке расстояние, пройденное автомобилем за 1 час

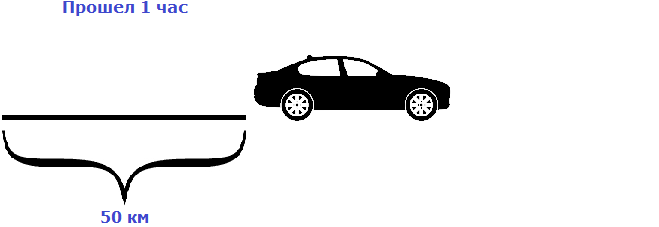
Пусть автомобиль проехал еще один час с той же скоростью, равной пятидесяти километрам в час. Тогда получится, что автомобиль проедет 100 км

Как видно из примера, увеличение времени в два раза привело к увеличению пройденного расстояния во столько же раз, то есть в два раза.

Такие величины, как время и расстояние называют прямо пропорциональными. А взаимосвязь между такими величинами называют прямой пропорциональностью.

Прямой пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой увеличение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая уменьшается во столько же раз.

Предположим, что изначально планировалось проехать на автомобиле 100 км за 2 часа, но проехав 50 км, водитель решил отдохнуть. Тогда получится, что уменьшив расстояние в два раза, время уменьшится во столько же раз. Другими словами, уменьшение пройденного расстояния приведет к уменьшению времени во столько же раз.

Интересная особенность прямо пропорциональных величин заключается в том, что их отношение всегда постоянно. То есть при изменении значений прямо пропорциональных величин, их отношение остается неизменным.

В рассмотренном примере расстояние сначала было равно 50 км, а время одному часу. Отношение расстояния ко времени есть число 50.

Но мы увеличили время движения в 2 раза, сделав его равным двум часам. В результате пройденное расстояние увеличилось во столько же раза, то есть стало равно 100 км. Отношение ста километров к двум часам опять же есть число 50

Число 50 называют коэффициентом прямой пропорциональности. Он показывает сколько расстояния приходится на час движения. В данном случае коэффициент играет роль скорости движения, поскольку скорость это отношение пройденного расстояния ко времени.

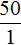
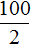
Из прямо пропорциональных величин можно составлять пропорции. К примеру, отношения и составляют пропорцию:

Это отношение можно прочитать следующим образом:

Пятьдесят километров так относятся к одному часу, как сто километров относятся к двум часам.

Пример 2. Стоимость и количество купленного товара являются прямо пропорциональными величинами. Если 1 кг конфет стоит 30 рублей, то 2 кг этих же конфет обойдутся в 60 рублей, 3 кг в 90 рублей. С увеличением стоимости купленного товара, его количество увеличивается во столько же раз.

Поскольку стоимость товара и его количество являются прямо пропорциональными величинами, то их отношение всегда постоянно.

Запишем чему равно отношение тридцати рублей к одному килограмму

Теперь запишем чему равно отношение шестидесяти рублей к двум килограммам. Это отношение опять же будет равно тридцати:

Здесь коэффициентом прямой пропорциональности является число 30. Этот коэффициент показывает сколько рублей приходится на килограмм конфет. В данном примере коэффициент играет роль цены одного килограмма товара, поскольку цена это отношение стоимости товара на его количество.

Обратная пропорциональность

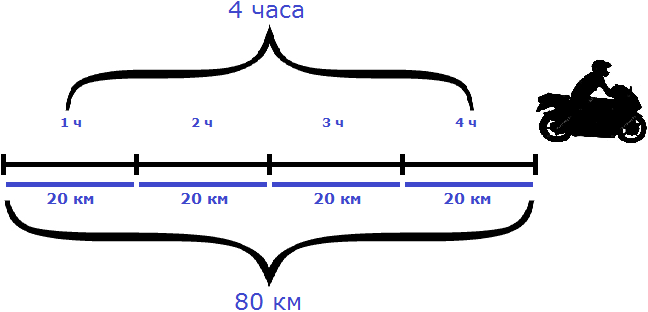
Рассмотрим следующий пример. Расстояние между двумя городами 80 км. Мотоциклист выехал из первого города, и со скоростью 20 км/ч доехал до второго города за 4 часа.

Если скорость мотоциклиста составила 20 км/ч это значит, что каждый час он проезжал расстояние равное двадцати километрам. Изобразим на рисунке расстояние, пройденное мотоциклистом, и время его движения:

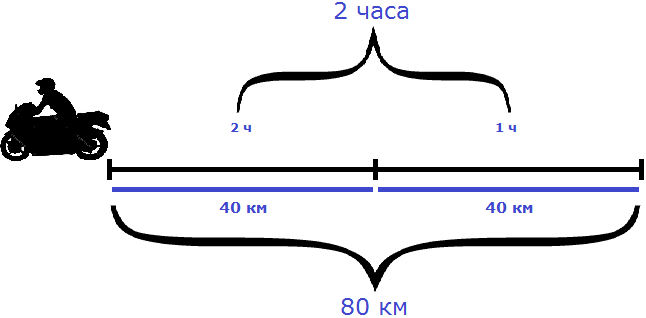
На обратном пути скорость мотоциклиста была 40 км/ч, и на тот же путь он затратил 2 часа.

Легко заметить, что при изменении скорости, время движения изменилось во столько же раз. Причем изменилось в обратную сторону — то есть скорость увеличилась, а время наоборот уменьшилось.

Такие величины, как скорость и время называют обратно пропорциональными. А взаимосвязь между такими величинами называют обратной пропорциональностью.

Обратной пропорциональностью называют взаимосвязь между двумя величинами, при которой увеличение одной из них влечет за собой уменьшение другой во столько же раз.

и наоборот, если одна величина уменьшается в определенное число раз, то другая увеличивается во столько же раз.

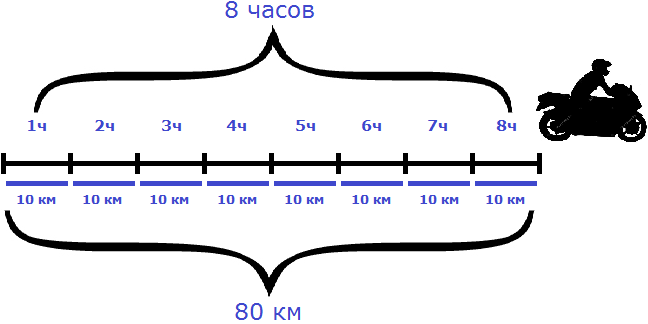
К примеру, если на обратном пути скорость мотоциклиста составила бы 10 км/ч, то те же 80 км он преодолел бы за 8 часов:

Как видно из примера, уменьшение скорости привело к увеличению времени движения во столько же раз.

Особенность обратно пропорциональных величин заключается в том, что их произведение всегда постоянно. То есть при изменении значений обратно пропорциональных величин, их произведение остается неизменным.

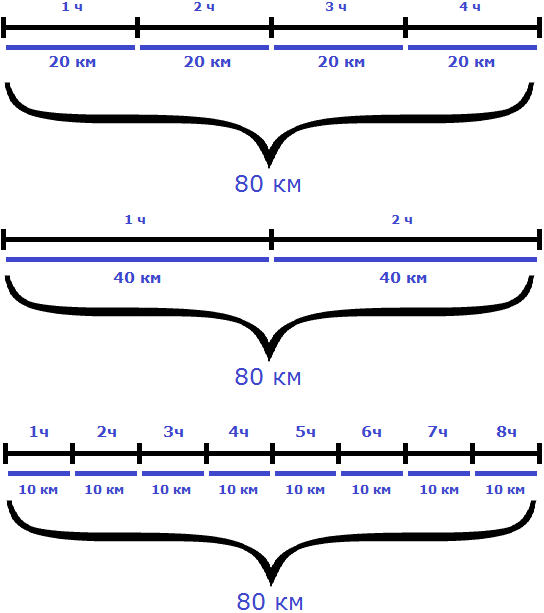
В рассмотренном примере расстояние между городами было равно 80 км. При изменении скорости и времени движения мотоциклиста, это расстояние всегда оставалось неизменным

Мотоциклист мог проехать это расстояние со скоростью 20 км/ч за 4 часа, и со скоростью 40 км/ч за 2 часа, и со скоростью 10 км/ч за 8 часов. Во всех случаях произведение скорости и времени было равно 80 км

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

10 thoughts on “Прямая и обратная пропорциональность”

что ценно теория методически верно преподается. очень добрый сайт.

мне теперь всё понятно, большое спасибо сайту

Источник

Пропорциональность

Содержание

Пример

Масса керосина пропорциональна его объёму: 2 л керосина имеют массу 1,6 кг, 5 л имеют массу 4 кг, 7 л имеют массу 5,6 кг. Отношение массы к объёму всегда будет равно плотности:

1,6 / 2 = 0,8; 4 / 5 = 0,8; 5,6 / 7 = 0,8 и т. д.

Коэффициент пропорциональности

Символ

Математический символ ‘∝’ используется для указания пропорциональности двух величин. Пример, A ∝ B.

В юникоде для отображения используется символ U+221D.

Прямая пропорциональность

Прямая пропорциональность — функциональная зависимость, при которой некоторая величина зависит от другой величины таким образом, что их отношение остаётся постоянным. Иначе говоря, эти переменные изменяются пропорционально, в равных долях, то есть, если аргумент изменился в два раза в каком-либо направлении, то и функция изменяется тоже в два раза в том же направлении.

Математически прямая пропорциональность записывается в виде формулы:

Графиком прямой пропорциональности является прямая линия, проходящая через начало координат.

Обратная пропорциональность

Обра́тная пропорциона́льность — это функциональная зависимость, при которой увеличение независимой величины(аргумента) вызывает пропорциональное уменьшение зависимой величины(функции).

См. также

Источники

Полезное

Смотреть что такое «Пропорциональность» в других словарях:

ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, пропорциональности, мн. нет, жен. (книжн.). 1. отвлеч. сущ. к пропорциональный. Пропорциональность частей. Пропорциональность телосложения. 2. Такая зависимость между величинами, когда они пропорционально (см. пропорциональный … Толковый словарь Ушакова

ПРОПОРЦИОНАЛЬНОСТЬ — (от лат. proportionalis соразмерный, пропорциональный). Соразмерность. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А.Н., 1910. ПРОПОРЦИОНАЛЬНОСТЬ отлат. proportionalis, пропорциональный. Соразмерность. Объяснение 25000… … Словарь иностранных слов русского языка

Пропорциональность — 1) соразмерность элементов и их связей в одной системе; 2) принцип организации политических систем и процессов, динамическая сбалансированность политической системы. В политологическом ракурсе «пропорциональность» подразумевает выяснение целого… … Политология. Словарь.

пропорциональность — соразмерность, соизмеримость; соответствие, стройность, гармоничность, рациональность, нормальность. Ant. непропорциональность, асимметрия Словарь русских синонимов. пропорциональность соразмерность Словарь синонимов русского языка. Практический… … Словарь синонимов

ПРОПОРЦИОНАЛЬНОСТЬ — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Современная энциклопедия

ПРОПОРЦИОНАЛЬНОСТЬ — простейший вид функциональной зависимости (см. Функция). Различают прямую пропорциональность. (y =kx) и обратную пропорциональность (y=k/x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S =vt… … Большой Энциклопедический словарь

Пропорциональность — (от латинского proportio соотношение), простейший вид функциональной зависимости. Различают прямую пропорциональность y=kx (например, путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т.е. S=vt) и обратную… … Иллюстрированный энциклопедический словарь

пропорциональность — ПРОПОРЦИОНАЛЬНОСТЬ, соразмерность ПРОПОРЦИОНАЛЬНЫЙ, соразмерный ПРОПОРЦИОНАЛЬНО, соразмерно, соответственно … Словарь-тезаурус синонимов русской речи

ПРОПОРЦИОНАЛЬНОСТЬ — ПРОПОРЦИОНАЛЬНОСТЬ, и, жен. 1. см. пропорциональный. 2. В математике: такая зависимость между величинами, при к рой увеличение одной из них влечёт за собой изменение другой во столько же раз. Прямая п. (при к рой с увеличением одной величины… … Толковый словарь Ожегова

ПРОПОРЦИОНАЛЬНОСТЬ — англ. proportionality; нем. Proportionalitat. Простейший вид функциональной зависимости, фиксирующей соотношение между двумя величинами; показатель отношения исследуемой функции ко всему числу изучаемых случайностей. Antinazi. Энциклопедия… … Энциклопедия социологии

ПРОПОРЦИОНАЛЬНОСТЬ — (лат. proportionalis) соблюдение пропорций, рациональных структурных соотношений в экономике, согласованное развитие отраслей, сфер, регионов. Райзберг Б.А., Лозовский Л.Ш., Стародубцева Е.Б.. Современный экономический словарь. 2 е изд., испр. М … Экономический словарь

Источник

Прямая и обратная пропорциональность

Всего получено оценок: 426.

Всего получено оценок: 426.

Прямая и обратная пропорциональность – это одна из основ математики и геометрии 6 класса. Причем, это та основа, знания которой пригодятся не только при решении задач, но и в реальной жизни: пропорциональны друг другу бывают физические величины, заработные платы и конфеты, купленные в магазине.

Что такое пропорция?

Пропорция – это взаимосвязь двух величин. То есть, если меняется одна величина, меняется и другая. Если одна величина пропорциональна другой, а друга пропорциональна третьей, то все эти величины связаны между собой. Разделяют прямую и обратную пропорцию. Дадим им определения и приведем наглядные примеры.

Прямая пропорция

Прямая пропорция – это взаимоотношение величин, при котором, увеличивая одну величину, мы автоматически увеличим другую. Самый простой пример это булочки в магазине и цена на них. Булочка в любом случае стоит 30 руб. Покупая одну штуку мы платим 30 руб.

Если увеличим размер покупки, то соразмерно возрастет и цена. Она не может не возрасти, ведь булочник не будет отдавать свой товар просто так. За 2 булочки мы заплатим 60 рублей, за 3 – 90 и так далее.

Если устанавливать зависимость между количеством булочек и ценой на них, то получится следующее отношение:

Цена булочек/количество=30/1=60/2 и так далее. Заметим, что всегда это отношение равно одному и тому же числу. В данном примере это число 30. Оно будет постоянным для любого варианта данной пропорции. Конкретно в данном примере это число является одновременно и ценой одной булочки.

Иными словами, для приведенного примера пропорциональность можно объяснить так: сколько бы булочек мы ни купили, все равно цена одной будет 30 рублей. Вот и все. В рамках математики говорят, что если коэффициент пропорциональности не меняется, то числа пропорциональны.

Для того, чтобы понять, изменяется коэффициент или нет, нужно просто поделить друг на друга числа этой пропорции и сравнить результат. То есть, взять сначала отношение цены одной булочки к ее количеству, а затем цены 30 булочек к их количеству. Коэффициент сохранит свое значение, значит эти числа прямопропорциональны.

Обратная пропорция

Существует также понятие обратной пропорции. Часто бывает так, что одна величина зависит от другой, но не прямопропорционально. Сравним две взаимосвязанные между собой величины. Например, мотоциклист залил в бак бензин. Чем меньше бензина остается в баке мотоциклиста, тем больше проехал водитель. Здесь на лицо обратная зависимость количества бензина и пройденного расстояния.

Как просто запомнить?

Есть 4 простые схемы запоминания темы, по две для каждого вида пропорциональности.

Для прямой пропорции всегда работает схема: «больше-больше» или «меньше-меньше». То есть при увеличении одной величины, увеличится и другая, или при уменьшении одной величины уменьшится другая.

Соответственно, для обратной пропорциональности наоборот: «больше-меньше» или «меньше-больше». То есть, чем больше одна величина, тем меньше другая и наоборот.

Что мы узнали?

Мы привели объяснение прямой и обратной пропорциональности. Вывели простые схемы для запоминания темы и обговорили понятные примеры.

Источник