Что значит прямая параллельна плоскости

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №4. Параллельность прямых, прямой и плоскости

Перечень вопросов, рассматриваемых в теме

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.

Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.

Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.

Теоретический материал для самостоятельного изучения

Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.

В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».

В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».

В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.

В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.

Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Проиллюстрировать данные определения наглядно нам поможет куб.

Давайте укажем некоторые пары параллельных прямых:

AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.

А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:

AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.

Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

Лемма. Если одна из двух паралельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.

Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.

Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство:

Выберем точку M на прямой b.

Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).

Возможны два случая:

1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.

Пусть прямая b пересекает плоскость α.

Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.

Теперь нужно доказать, что прямые a и b параллельны.

Пусть у прямых a и b есть общая точка L.

Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.

Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.

Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.

Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.

Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.

Существует еще два утверждения, которые используются при решении задач:

Примеры и разбор решения заданий тренировочного модуля

Тип задания: Ввод с клавиатуры пропущенных элементов в тексте

Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.

Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10

Т.к. ACFE − параллелограмм, то АС=EF=10

Тип задания: Единичный / множественный выбор

Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.

MC

Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит

. BC=AD= 8 см;

Источник

Параллельность прямой и плоскости

Урок 6. Геометрия 10 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Параллельность прямой и плоскости»

· рассмотрим параллельность прямой и плоскости, как один из трех возможных вариантов их взаимного расположения в пространстве;

· сформулируем и докажем теорему о параллельности прямой и плоскости;

· докажем еще два утверждения, которые часто применяют при решении задач.

Раньше мы с вами уже узнали аксиомы стереометрии. На этом уроке нам понадобится вторая аксиома: если две точки прямой принадлежат плоскости, то и вся прямая принадлежит плоскости.

Отсюда вытекают три случая взаимного расположения прямой и плоскости в пространстве.

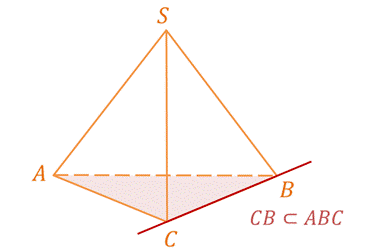
Первый случай. Прямая лежит в плоскости, т.е. каждая точка прямой лежит в плоскости. Например, если SABC – треугольная пирамида, то прямая CB лежит в плоскости ABC.

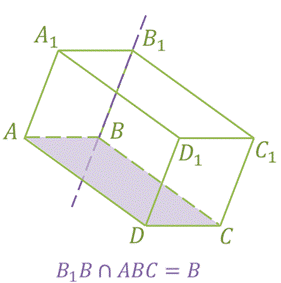
Второй случай. Прямая и плоскость пересекаются, т.е. имеют только одну общую точку. Например, прямая B₁B пересекается с плоскостью грани ABCD параллелепипеда ABCDA₁B₁C₁D₁.

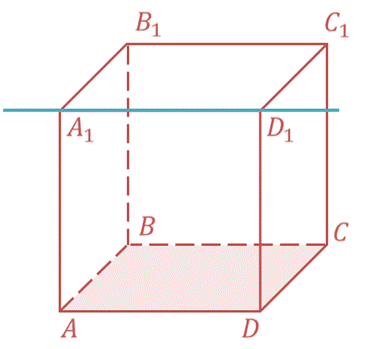
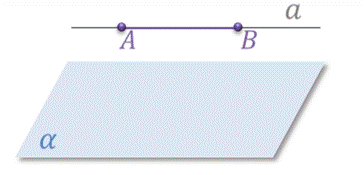
И третий случай. Прямая и плоскость не имеют ни одной общей точки. Например, если ABCDA₁B₁C₁D₁– куб, то прямая A₁D₁ и плоскость, в которой лежит грань ABCD, не пересекаются.

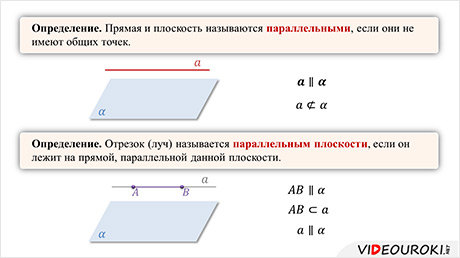
Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Параллельность прямой а и плоскости α обозначается следующим образом 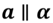. Читают: «Прямая a параллельна плоскости α».

Отрезок (луч) называется параллельным плоскости, если он лежит на прямой, параллельной данной плоскости.

Приведем несколько примеров параллельности прямой и плоскости.

Вот возьмем, к примеру, гитару. Натянутая гитарная струна и плоскость грифа параллельны. Линии электропередач параллельны плоскости земли.

Еще примером может послужить линия пересечения стены и потолка. Эта линия параллельна плоскости пола.

Обратите внимание, в плоскости пола также есть прямая, параллельная этой линии. Такой прямой является, например, линия пересечения пола с той же самой стеной.

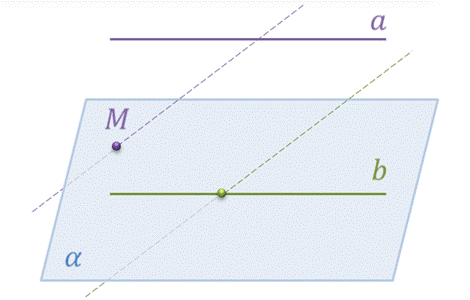
Прямые о которых мы сейчас говорили, обозначены буквами а и b. Оказывается, что если в плоскости α имеется прямая b, параллельная прямой а, не лежащая в плоскости α, то прямая а и плоскость α параллельны.

Это утверждение (теорема) является признаком, по которому можно сделать вывод о параллельности прямой а и плоскости α.

Теорема. Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна данной плоскости.

Докажем теорему. Пусть у нас есть две параллельные прямые а и b и плоскость α. Причем они расположены так, что прямая b лежит в плоскости α, а прямая а не лежит в этой плоскости. Докажем, что прямая а параллельна плоскости α.

Предположим, что прямая а пересекает плоскость α в некоторой точке М. А значит, по лемме о пересечении плоскости параллельными прямыми прямая b также должна пересекать плоскость α. Но это невозможно, так как прямая b лежит в плоскости α по условию. Таким образом, наше предположение неверно. И прямая а не пересекает плоскость α. По условию она не лежит в плоскости α. Следовательно, прямая а параллельна плоскости α. Теорема доказана.

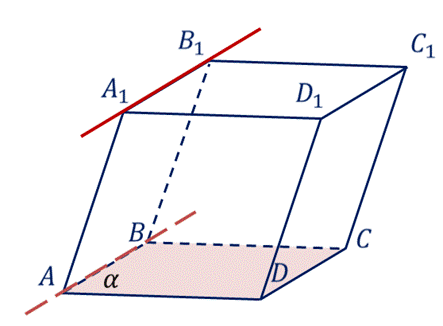
На рисунке изображен параллелепипед ABCDA₁B₁C₁D₁. Прямая A₁B₁ параллельна плоскости α, в которой лежит грань ABCD. Действительно, прямая A₁B₁ параллельна прямой AB, лежащей в плоскости α. Следовательно, по признаку параллельности прямой и плоскости A₁B₁ параллельна α.

Докажем еще два утверждения, которые часто применяются при решении задач.

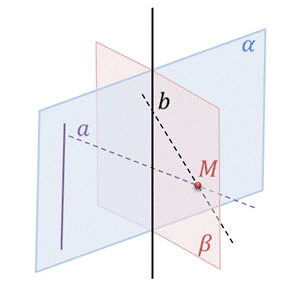
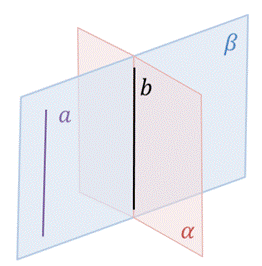
Первое утверждение. Если плоскость проходит через данную прямую, параллельную другой плоскости, и пересекает эту плоскость, то линия пересечения плоскостей параллельна данной прямой.

Докажем это утверждение. Пусть плоскость α проходит через прямую а, параллельную плоскости β. И плоскости α и β пересекаются по прямой b. Докажем, что прямая а параллельна прямой b.

Действительно, эти прямые лежат в одной плоскости (в плоскости α) и не пересекаются: ведь в противном случае, если бы прямые а и b пересекались в некоторой точке М, тогда бы прямая а пересекала плоскость β в точке М. Что невозможно, поскольку прямая а параллельна плоскости β по условию.

Таким образом, прямые а и b параллельны. Что и требовалось доказать.

Второе утверждение. Если одна из двух параллельных прямых параллельна данной плоскости, то другая прямая либо также параллельна данной плоскости, либо лежит в этой плоскости.

Доказательство. Пусть прямые а и b параллельны. Причем прямая а параллельна плоскости α. Тогда прямая а не пересекает плоскость α, и, следовательно, по лемме о пересечении плоскости параллельными прямыми прямая b также не пересекает плоскость α. А значит, прямая b либо параллельна плоскости α, либо лежит в этой плоскости. Что и требовалось доказать.

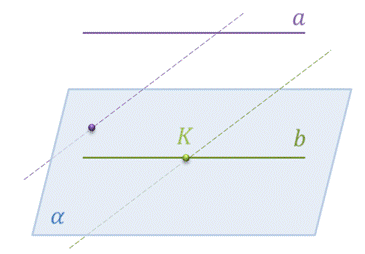
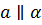
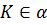
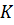
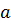
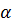
Задача. Прямая . Точка . Докажите, что прямая, проходящая через точку и параллельная прямой , лежит в .

Доказательство. Пусть прямая b проходит через точку K и параллельна прямой а.

Предположим, что прямая b не лежит в плоскости α, т.е. пересекает плоскость α в точке К. Тогда прямая а также пересекает плоскость α по лемме о пересечении плоскости параллельными прямыми. А это противоречит условию. Следовательно, прямая b лежит в плоскости α. Что и требовалось доказать.

Подведем итоги урока. На этом уроке мы рассмотрели параллельность прямой и плоскости, как один из трех возможных вариантов их взаимного расположения в пространстве. Сформулировали и доказали признак параллельности прямой и плоскости. А также доказали два утверждения, которые часто применяют при решении задач.

Источник

Геометрия. 10 класс

Конспект урока

Геометрия, 10 класс

Урок №4. Параллельность прямых, прямой и плоскости

Перечень вопросов, рассматриваемых в теме

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые − прямые, которые не лежат в одной плоскости.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Атанасян Л. С., Бутузов В. Ф., Кадомцев С. Б. и др. Геометрия 10-11 кл.– М.: Просвещение, 2014. 255 с.

Зив Б. Г. Дидактические материалы. Геометрия 10 кл. – М.: Просвещение, 2014. 96 с.

Глазков Ю. А., Юдина И. И., Бутузов В.Ф. Рабочая тетрадь. Геометрия 10 кл.-М.: Просвещение, 2013. 65 с.

Теоретический материал для самостоятельного изучения

Геометрия, которую мы изучаем, называется евклидовой, по имени древнегреческого ученого Евклида (3 век до нашей эры), который создал целый труд по математике под названием «Начала». В данной книге есть раздел о параллельных прямых.

В советском энциклопедическом словаре слово «параллельность» переводится с греческого языка, как «идущий рядом».

В средние века параллельность обозначалась знаком «=». В 1557 году Р. Рекордом для обозначения равенства был введен знак «=», которым мы пользуемся сейчас, а параллельность стали обозначать «║».

В книге «Начала» определение параллельных прямых звучало так «прямые, лежащие в одной плоскости и будучи бесконечно продолжены в обе стороны, ни с той, ни с другой стороны не пересекаются». Это определение почти не отличается от современного.

В области параллельных прямых работало очень много учёных: Н.И. Лобаческий (18-19 век); Аббас ал-Джаухари (работал в Багдаде в 9 веке); Фадл ал-Найризи (Богдад 10 век); Герард (Италия 12 век); Иоганн Генрих Ламберт (Берлин) и многие другие.

Каково расположение 2-х прямых на плоскости (совпадают, пересекаются, параллельны) (рис. 1 а, б, в).

Определение. Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

Определение. Скрещивающиеся прямые — прямые, которые не лежат в одной плоскости.

Проиллюстрировать данные определения наглядно нам поможет куб.

Давайте укажем некоторые пары параллельных прямых:

AB||A₁B₁; AB|| CD; A₁B₁||C₁D₁; CD||C₁D₁; AD||A₁D₁; BC||B₁D₁; AD||BC; A₁D₁||B₁C₁.

А теперь рассмотрим некоторые пары скрещивающихся прямых, как мы отметили, они не должны лежать в одной плоскости:

AB A₁D₁; AB B₁C₁; CD A₁D₁; CD B₁C₁; BC C₁D₁; BC A₁B₁; AB B₁C₁; AB A₁D₁.

Теорема. Через любую точку пространства, не лежащую на данной прямой, проходит прямая, параллельная данной, и притом только одна.

Определение. Два отрезка называются параллельными, если они лежат на паралельных прямых.

Аналогично определяется праралельность отрезка и прямой, а так же паралельность двух лучей.

Лемма. Если одна из двух паралельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

Если в этой плоскости одна из параллельных прямых b пересекает прямую p, то вторая прямая a тоже пересекает p.

Так как точка N находится на прямой p, то N находится в плоскости α и является единственной общей точкой прямой a и плоскости α.

Нам известно из курса планиметрии, что если три прямые лежат в одной плоскости и две из них параллельны третьей, то эти две прямые параллельны. Похожее утверждение имеет место и для трех прямых в пространстве.

Теорема. Если две прямые параллельны третьей прямой, то они параллельны.

Доказательство:

Выберем точку M на прямой b.

Через точку M и прямую a, которая не содержит эту точку, можно провести только одну плоскость α (Через прямую и не лежащую на ней точку можно провести только одну плоскость).

Возможны два случая:

1) прямая b пересекает плоскость α или 2) прямая b находится в плоскости α.

Пусть прямая b пересекает плоскость α.

Значит, прямая c, которая параллельна прямой b, тоже пересекает плоскость α. Так как a∥c, то получается, что a тоже пересекает эту плоскость. Но прямая a не может одновременно пересекать плоскость α и находиться в плоскости α. Получаем противоречие, следовательно, предположение, что прямая b пересекает плоскость α, является неверным. Значит, прямая b находится в плоскости α.

Теперь нужно доказать, что прямые a и b параллельны.

Пусть у прямых a и b есть общая точка L.

Это означает, что через точку L проведены две прямые a и b, которые параллельны прямой c. Но по второй теореме это невозможно. Поэтому предположение неверное, и прямые a и b не имеют общих точек.

Так как прямые a и b находятся в одной плоскости α и у них нет общих точек, то они параллельны.

Если две точки прямой лежат в данной плоскости, то по аксиоме А₂ вся прямая лежит в этой плоскости. Из этого следует, что возможны три расположения прямой и плоскости:

Определение. Прямая и плоскость называются параллельными, если они не имеют общих точек.

Наглядный пример, который дает представление о прямой, параллельной плоскости- это линия пересечения стены и потолка-она параллельна плоскости пола.

Теорема (Признак параллельности прямой и плоскости)
Если прямая, не лежащая в данной плоскости, параллельна какой-нибудь прямой на этой плоскости, то эта прямая параллельна данной плоскости.

Доказательство:
Доказательство проведем от противного. Пусть a не параллельна плоскости α, тогда прямая a пересекает плоскость в некоторой точке A. Причем A не находится на b, так как a∥b. Согласно признаку скрещивающихся прямых, прямые a и b скрещивающиеся.

Мы пришли к противоречию. Так как согласно данной информации a∥b, они не могут быть скрещивающимися. Значит, прямая a должна быть параллельна плоскости α.

Существует еще два утверждения, которые используются при решении задач:

Примеры и разбор решения заданий тренировочного модуля

Тип задания: Ввод с клавиатуры пропущенных элементов в тексте

Дано: в ∆ АВС КМ − средняя линия, КМ=5; ACFE- параллелограмм.

Решение: Т.к. КМ − средняя линия, то АС= 2·КМ, то АС=2·7=10

Т.к. ACFE − параллелограмм, то АС=EF=10

Тип задания: Единичный / множественный выбор

Точка М не лежит в плоскости ромба ABCD. На отрезке АМ выбрана точка Е так, что MЕ:ЕА=1:3. Точка F – точка пересечения прямой МВ с плоскостью CDE. Найдите АВ, если AD= 8 cм.

MC

Т.к. AD||BC||FK, следовательно, треугольники MFK и MBC- подобны (по трем углам). Значит

. BC=AD= 8 см;

Источник