Что значит провести ось симметрии
Урок математики. Тема: «Ось симметрии»
Разделы: Математика
Перед каждым лежат ножницы и лист бумаги.
– Возьмем лист бумаги, сложим его попалам и вырежем какую-нибудь фигурку. Теперь развернем лист и посмотрим на линию сгиба.
Вопрос: Какую функцию выполняет эта линия?
Предполагаемый ответ: Эта линия делит фигуру пополам.
Вопрос: Как расположены все точки фигуры на двух получившихся половинках?
Предполагаемый ответ: Все точки половинок находятся на равном расстоянии от линии сгиба и на одном уровне.
– Значит, линия сгиба делит фигурку пополам так, что 1 половинка является копией 2 половинки, т.е. эта линия непростая, она обладает замечательным свойством (все точки относительно ее находятся на одинаковом расстоянии), эта линия – ось симметрии.
– Вырезать снежинку, найти ось симметрии, охарактеризовать ее.
– Начертить в тетради окружность.
Вопрос: Определить, как проходит ось симметрии?
Предполагаемый ответ: По-разному.
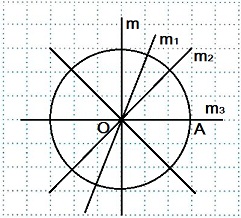
Вопрос: Так сколько осей симметрии имеет окружность?
Предполагаемый ответ: Много.
– Правильно, окружность имеет множество осей симметрии. Такой же замечательной фигурой является шар (пространственная фигура)
Вопрос: Какие еще фигуры имеют не одну ось симметрии?
Предполагаемый ответ: Квадрат, прямоугольник, равнобедренный и равносторонний треугольники.
– Рассмотрим объемные фигуры: куб, пирамиду, конус, цилиндр и т.д. Эти фигуры тоже имеют ось симметрии. Определите, сколько осей симметрии у квадрата, прямоугольника, равностороннего треугольника и у предложенных объемных фигур?
Раздаю учащимся половинки фигурок из пластилина.
– Используя полученную информацию, долепить недостающую часть фигурки.
Примечание: фигурка может быть и плоскостной, и объемной. Важно, чтобы учащиеся определили, как проходит ось симметрии, и долепили недостающий элемент. Правильность выполнения определяет сосед по парте, оценивает, насколько правильно проделана работа.
Из шнурка одного цвета на рабочем столе выложена линия (замкнутая, незамкнутая, с самопересечением, без самопересечения).
Задание 5 (групповая работа 5 мин).
– Определить визуально ось симметрии и относительно нее достроить из шнурка другого цвета вторую часть.
Правильность выполненной работы определяется самими учениками.
Перед учащимися представлены элементы рисунков
– Найдите симметричные части этих рисунков.
Для закрепления пройденного материала предлагаю следующие задания, предусмотренные на 15 мин.:
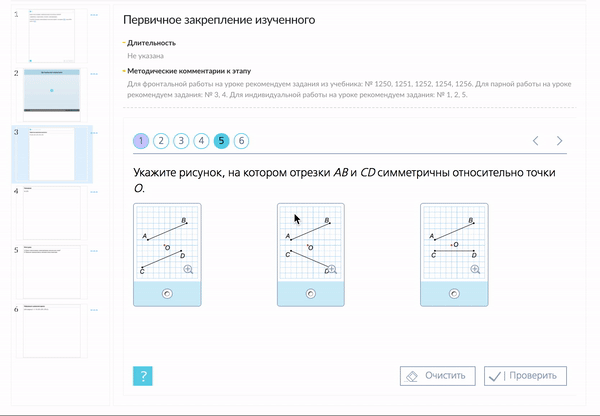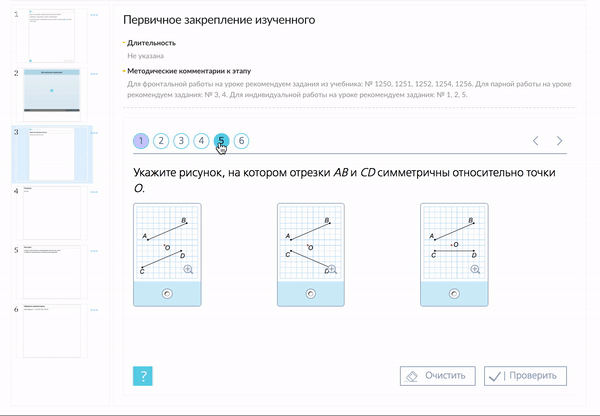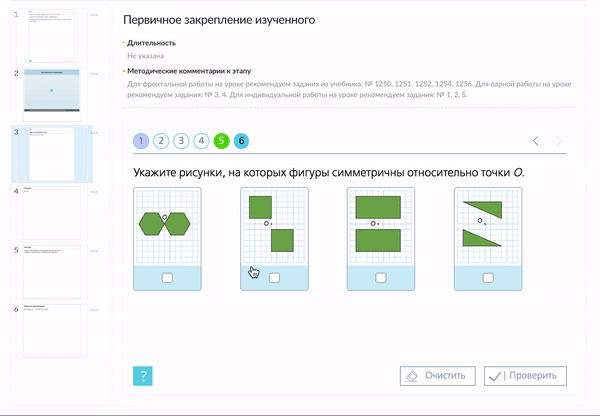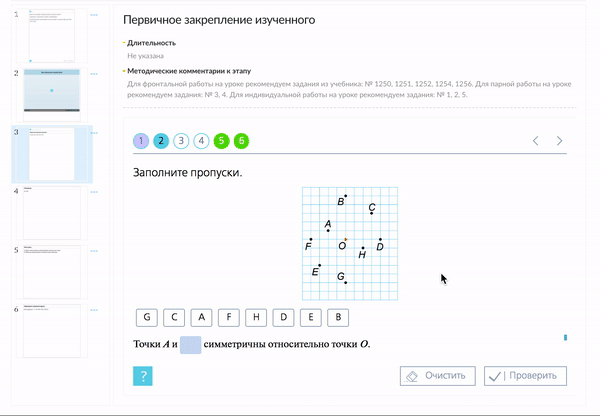
1. Прямая ОР – ось симметрии треугольника КОМ.
Назовите все равные элементы треугольника КОР и КОМ. Каков вид этих треугольников?
2. Начертите в тетради несколько равнобедренных треугольников с общим основанием равным 6 см.
3. Начертите отрезок АВ. Постройте прямую перпендикулярную отрезку АВ и проходящую через его середину. Отметьте на ней точки С и D так, чтобы четырехугольник АСВD был симметричен относительно прямой АВ.
– Наши первоначальные представления о форме относятся к очень отдаленной эпохе древнего каменного века – палеолита. В течение сотен тысячелетий этого периода люди жили в пещерах, в условиях мало отличавшихся от жизни животных. Люди изготовляли орудия для охоты и рыболовства, вырабатывали язык для общения друг с другом, а в эпоху позднего палеолита украшали свое существование, создавая произведения искусства, статуэтки и рисунки, в которых обнаруживается замечательное чувство формы.
Когда произошел переход от простого собирания пищи к активному ее производству, от охоты и рыболовства к земледелию, человечество вступает в новый каменный век, в неолит.
Человек неолита обладал острым чувством геометрической формы. Обжиг и раскраска глиняных сосудов, изготовление камышовых циновок, корзин, тканей, позже – обработка металлов вырабатывали представления о плоскостных и пространственных фигурах. Неолитические орнаменты радовали глаз, выявляя равенство и симметрию.
– А где в природе встречается симметрия?
Предполагаемый ответ: крылья бабочек, жуков, листья деревьев…
– Симметрию можно наблюдать и в архитектуре. Строя здания, строители четко придерживаются симметрии.
Поэтому здания получаются такие красивые. Также примером симметрии служит человек, животные.
1. Придумать свой орнамент, изобразить его на листе формат А4 (можно нарисовать в виде ковра).
2. Нарисовать бабочек, отметить, где присутствуют элементы симметрии.
Осевая симметрия
Осевая симметрия — это симметрия относительно прямой.

Чтобы построить точку, симметричную некоторой точке A относительно прямой g, надо:
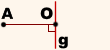

Полученная точка A1 симметрична точке A относительно прямой g.
Прямая g называется осью симметрии.
Таким образом, точки A и A1 симметричны относительно прямой g, если эта прямая проходит через середину отрезка AA1 и перпендикулярна к нему.
Если точка A лежит на прямой g, то симметричная ей точка есть сама точка A.
Преобразование фигуры F в фигуру F1, при котором каждая её точка A переходит в точку A1, симметричную относительно данной прямой g, называется преобразованием симметрии относительно прямой g.
Фигуры F и F1 называются фигурами, симметричными относительно прямой g.

Например, треугольники ABC и A1B1C1 симметричны относительно прямой g.
Если преобразование симметрии относительно прямой g переводит фигуру в себя, то такая фигура называется симметричной относительно прямой g, а прямая g называется её осью симметрии.
Симметричная фигура своей осью симметрии делится на две равные половины. Если симметричную фигуру нарисовать на бумаге, вырезать и согнуть по оси симметрии, то эти половинки совпадут.
Примеры фигур, симметричных относительно прямой.

Прямоугольник имеет 2 оси симметрии: прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
Ромб имеет две оси симметрии:
прямые, на которых лежат его диагонали.
3) Квадрат, как ромб и прямоугольник, имеет четыре оси симметрии: прямые, содержащие его диагонали, и прямые, проходящие через точку пересечения диагоналей параллельно сторонам.
Окружность имеет бесконечное множество осей симметрии:
любая прямая, содержащая диаметр, является осью симметрии окружности.
Прямая также имеет бесконечное множество осей симметрии: любая перпендикулярная ей прямая является для данной прямой осью симметрии.
Равнобедренная трапеция — фигура, симметричная относительно прямой,перпендикулярной основаниям и проходящей через их середины.
Равнобедренный треугольник имеет одну ось симметрии:
прямую, проходящую через высоту (медиану, биссектрису), проведённую к основанию.
8) Равносторонний треугольник.
Равносторонний треугольник имеет три оси симметрии:
прямые, содержащие его высоты (медианы, биссектрисы).
Угол — фигура, симметричная относительно прямой, содержащей его биссектрису.
Осевая симметрия является движением.
6.7.3. Осевая симметрия
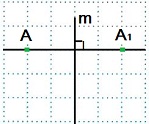
m – ось симметрии.
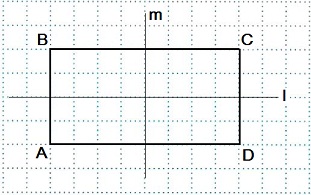
Если чертеж перегнуть по прямой m или по прямой l, то обе части чертежа совпадут.
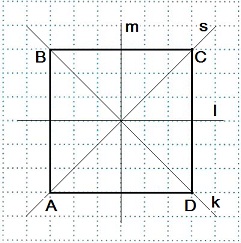
Если квадрат перегнуть по какой-либо из прямых: m, l, k или s, то обе части квадрата совпадут.
Задание. Построить точку А1, симметричную точке А(-4; 2) относительно оси Ох.
Построить точку А2, симметричную точке А(-4; 2) относительно оси Оy.
У точек, симметричных относительно оси Ох абсциссы совпадают, а ординаты являются противоположными числами.
У точек, симметричных относительно оси Оу ординаты совпадают, а абсциссы являются противоположными числами.
Осевая и центральная симметрии. Проводим урок с ЭФУ
Повторение материала
Из курса математики 5 класса учащиеся уже узнали, как выглядят и строятся фигуры, имеющие ось симметрии. Перед изучением темы «Осевая и центральная симметрии» будет целесообразно повторить материал 5 класса. Следует разъяснить учащимся, что построение фигуры во многих случаях возможно по положению ключевых точек.
Для закрепления этого интуитивно-наглядного понимания, учитель может предложить детям перегнуть лист бумаги, на котором изображены симметричные фигуры.
Понятие симметрии
Слово «симметрия» происходит от греческого symmetria, что означает соразмерность. В нашем случае, симметрия — это свойство геометрических фигур к отображению.
Учитель: Симметрия используется в рисунках, орнаментах, архитектуре с давних времен. Где еще симметрию могут использовать люди?
Ученики: при строительстве домов; в изготовлении предметов быта.
Учитель: верно, но ведь симметрия распространена не только там, где творил человек! Мы видим симметричные объекты природы каждый день. Назовите мне три таких объекта!
Ученики: Бабочка, цветы, форма листа! Морская звезда, снежинка, яблоко в разрезе.
Симметрий, как это не покажется вам странным и любопытным, много, но мы будем рассматривать две симметрии на плоскости: относительно точки и прямой.
Осевая симметрия
Осевая симметрия — это симметрия относительно проведённой прямой (оси).
Заметим, что любые две фигуры, симметричные относительно некоторой прямой, равны (Рис.131). Все точки фигуры, имеющей ось симметрии, не принадлежащие этой оси, можно разделить на пары симметричных точек (Рис. 132).
Центральная симметрия
Симметрию относительно точки называют центральной симметрией.
Фигуры, имеющие центр симметрии — понятие, воспринимающееся учащимися сложнее, чем фигуры, имеющие ось симметрии. Для удобства восприятия и понимания, рекомендуется привести как можно больше примеров из окружающей природы.
В зависимости от уровня математической подготовки учащихся класса, можно обратить их внимание на то, что прямая — это фигура, имеющая бесконечно много осей и центров симметрии.
С помощью заданий из «Классной работы» материал можно закрепить в различных графических форматах.
Актуализация знаний
Предложите ребятам решить задание № 1260. Какие печатные буквы русского алфавита имеют 1) вертикальную ось симметрии; 2) горизонтальную ось симметрии; 3) горизонтальную и вертикальную оси?
Готовый яркий раздаточный материал «Алфавит» вы можете скачать в конце этой статьи.
Также рекомендуем вам применять на уроке различные методы преподнесения информации: как визуальный, так и аудио. Попробуйте аудиодиктант.
Осевая симметрия
Отражательная симметрия. В евклидовой геометрии осевая симметрия — вид движения (зеркального отражения), при котором множеством неподвижных точек является прямая, называемая осью симметрии. Отсюда следует, что любой точке соответствует точка, находящаяся на том же расстоянии от оси симметрии, и лежащая на одной прямой с исходной точкой и их общей проекцией на ось симметрии. Например, плоская фигура прямоугольник в пространстве осесимметрична и имеет 3 оси симметрии (две диагонали — в плоскости фигуры; если это не квадрат с двумя дополнительными осями — медиатрисами сторон), а параллелограмм общего вида имеет одну ось симметрии (проходящую через центр перпендикулярно плоскости).
Вращательная симметрия. В естественных науках под осевой симметрией понимают вращательную симметрию (другие термины — радиальная, аксиальная (англ. axial – осевой), поворотная, лучевая симметрии) относительно поворотов вокруг прямой. При этом тело (фигуру, задачу, организм) называют осесимметричными, если они переходят в себя при любом (например, малом) повороте вокруг этой прямой. В этом случае, прямоугольник не будет осесимметричным телом, но, например, конус будет.Применительно к плоскости эти два вида симметрии совпадают (считаем, что ось тоже принадлежит этой плоскости).
В кристаллографии вводят также (осевую) симметрию некоторого порядка:
Осевая симметрия n-го порядка — симметричность относительно поворотов на угол 360°/n вокруг какой-либо оси. Описывается группой Zn.
* Тогда симметрия в первом смысле (см. выше) является осевой симметрией второго порядка, а во втором — ∞-го порядка, так как поворот на любой сколь угодно малый угол приводит к совмещению фигуры с самой собой. Примеры: шар, цилиндр, конус.
* Оси симметрии 2-го, 3-го, 4-го, 6-го и даже 5-го порядка (кристаллы с непериодическим пространственным расположением атомов (мозаика Пенроуза)) можно наблюдать на примере кристаллов.
Зеркально поворотная осевая симметрия n-го порядка — поворот на 360°/n и отражение в плоскости, перпендикулярной данной оси.Оси симметрии порядка выше 2-го называются осями симметрии высшего порядка.
Связанные понятия
Упоминания в литературе
Связанные понятия (продолжение)
Согласно Математической Энциклопедии, спиралями называются плоские кривые, которые «обычно обходят вокруг одной (или нескольких точек), приближаясь или удаляясь от неё». Это толкование термина не является строго формализуемым определением. Если какая-то известная кривая содержит в названии эпитет «спираль», то к этому следует относиться как к исторически сложившемуся названию.
Говорят, что два и более объектов концентричны или коаксиальны, если они имеют один и тот же центр или ось. Окружности, правильные многоугольники, правильные многогранники и сферы могут быть концентричны друг другу (имея одну и ту же центральную точку), как могут быть концентричными и цилиндры (имея общую коаксиальную ось).
В геометрии фигуру называют хиральной (и говорят, что она обладает хиральностью), если она не совпадает со своим зеркальным отображением, точнее, не может быть совмещена с ним только вращениями и параллельными переносами. Хиральная фигура и её зеркальный образ называют энантиоморфами. Слово хиральность происходит от др.-греч. χειρ (хеир) — «рука». Это самый известный хиральный объект. Слово энантиоморф происходит от др.-греч. εναντιος (энантиос) — «противоположный», и μορφη (морфе) — «форма». Нехиральный.
Три вектора (или большее число) называются компланарными, если они, будучи приведёнными к общему началу, лежат в одной плоскости.