Что значит простые числа в математике 6 класс
Простые и составные числа
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Основные определения
Натуральные числа больше единицы бывают простые и составные.
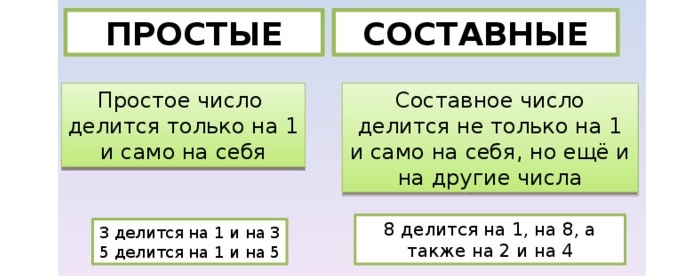
Простое число — это натуральное число больше 1, у которого есть всего два делителя: единица и само число.
Составное число — похоже на простое. Это точно такое же натуральное число больше единицы, которое делится на единицу, на само себя и еще хотя бы на одно натуральное число.
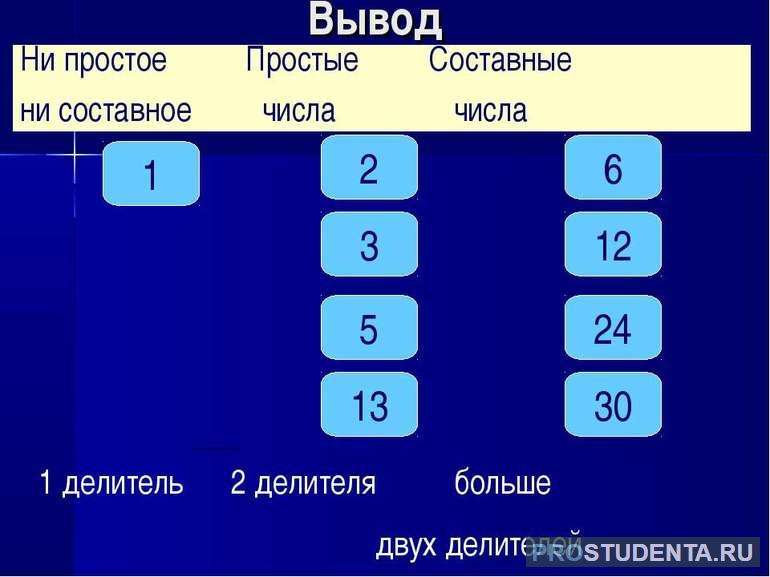
Число 1 — не является ни простым, ни составным числом, так как у него только один делитель — 1. Именно этим оно отличается от всех остальных натуральных чисел.
Число 2 — первое наименьшее простое, единственное четное, простое число. Все остальные — нечетные.
Число 4 — первое наименьшее составное число.
В математике есть первые простые и составные числа, но последних таких чисел не существует.
А еще не существует простых чисел, которые оканчиваются на 4, 6, 8 или 0. В числе простых есть только одно число, которое заканчивается на 2 — и это само число 2. Из оканчивающихся на 5 — число 5. Все остальные оканчиваются на 1, 3, 7 или 9, за исключением 21, 27, 33 и 39.
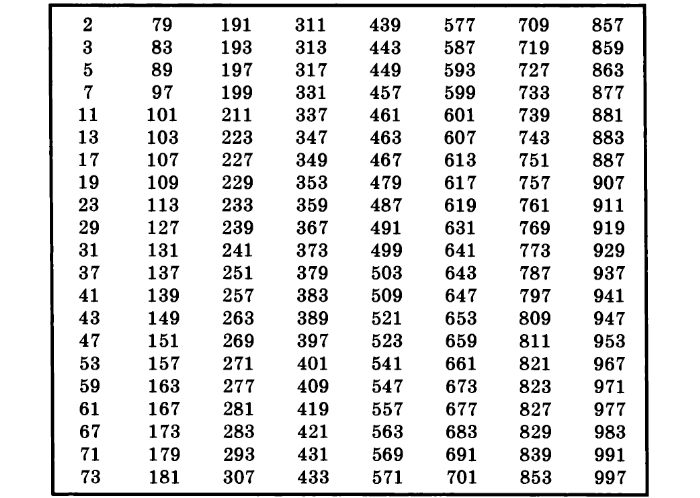
Таблица простых чисел до 1000
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 |
| 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 |
| 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 |
| 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 |
| 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 |
| 257 | 263 | 269 | 271 | 277 | 281 | 283 | 293 | 307 |
| 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 |
| 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 | 419 |
| 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 |
| 541 | 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 |
| 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 |
| 647 | 653 | 659 | 661 | 673 | 677 | 683 | 691 | 701 |
| 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 |
| 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 |
| 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 |
| 967 | 971 | 977 | 983 | 991 | 997 |
Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.
Нахождение простых и составных чисел (математика, 6 класс)
Выявление принадлежности величины в математике (6 класс) к простому или составному числу — задача непростая, когда под рукой нет специальных таблиц или средств вычислительной техники (компьютеров, планшетов, смартфонов) с предустановленным специализированным программным обеспечением. Однако специалисты предлагают уникальную методику, позволяющую решить поставленную задачу.
Выявление принадлежности величины в математике (6 класс) к простому или составному числу — задача непростая, когда под рукой нет специальных таблиц или средств вычислительной техники (компьютеров, планшетов, смартфонов) с предустановленным специализированным программным обеспечением. Однако специалисты предлагают уникальную методику, позволяющую решить поставленную задачу.
Общие сведения
Для использования алгоритма идентификации чисел нужны определенные знания. Начинать следует с расшифровки терминов. Любое число состоит из набора математических символов, которые называются цифрами. Последние располагаются в специальной разрядной сетке. Следует отметить, что каждый элемент, находящийся в ней, имеет определенное значение: единицы, десятки, сотни, тысячи, десятитысячи и т. д.
Кроме того, компонент «единицы» всегда будет меньше старшего следующего разряда. Для примера нужно обратить внимание на число 24. Оно состоит из разрядной сетки, которая включает в себя два элемента: единицы — 4 и десятки — 2. Математическая форма записи выглядит таким образом: 2*10+4*1. Однако единица не пишется, поскольку при умножении ее на любое число получается искомое значение.
Специалисты рекомендуют провести тест, показывающий уровень усвоения материала. Для его реализации необходимо написать любое число и разложить его на компоненты разрядной сетки. После того как все операции будут выполняться без ошибок, необходимо переходить к классификации чисел. Они бывают только двух видов:
Простые — числовые величины, которые не имеют множителей, кроме единицы и эквивалентных самим себе значений. Например, 7 делится только на 1 и 7. Сложной называется величина, содержащая множители, отличные от 1 и эквивалентного значения. Следует отметить, что синонимом сложного числа является составное, т. е. эти два термина имеют одну суть.
Можно разобрать для примера число 6. Оно является составным, поскольку его компоненты — двойка и тройка. При произведении последних по таблице умножения Пифагора получается шестерка. В учебнике, авторами которого являются Мерзляк А. Г. и Полонский В. Б., в конце находится таблица составных чисел до 1000. Кроме того, в учебном пособии можно также найти табличные величины простых значений в интервале от 1 до 1000.
Однако на контрольных работах учебники не всегда оказываются под рукой. В этом случае будет полезен алгоритм определения принадлежности величин к одному из типов.
Алгоритм идентификации
Методика — совокупность отдельных шагов, направленных на решение поставленной задачи. Специалисты предлагают специальный алгоритм, позволяющий определить, является число простым или составным. Чтобы им воспользоваться, нужно разобрать подробно критерии деления одного численного значения на другое, которые будут «телом» или основной частью алгоритма.
Следует отметить, что признаки делимости можно применять и на уроках информатики при написании простейших программ на языках программирования, которые изучаются в учебном заведении.
Как утверждают специалисты в области информационных технологий, математика и программирование тесно связаны между собой.
При желании ученик, имея базовые математические знания, может изучать языки программирования самостоятельно. Этот навык пригодится при обучении в высших учебных заведениях. Далее необходимо перейти к изучению самих критериев целочисленного деления двух чисел.
Критерии делимости
Признаки делимости — совокупность правил целочисленного деления одного числа на другое с учетом сомножителей, отличных от 1 и самого делимого. Чтобы не путаться в терминах, нужно записать в математической форме операцию деления (q/p=u), а также разобрать каждый из ее элементов.
Деление состоит минимум из трех компонентов: делимого (q), делителя (p) и их частного (u). Первый элемент является результатом произведения второго на третий. Иными словами, это число, которое нужно поделить на некоторую величину.
Делителем называется целочисленная величина, входящая в состав делимого. Результатом операции называется частное. Последнее является также одним из сомножителей. Математики утверждают, что обратной операцией умножения считается деление, т. е. делимое — это произведение, делитель — I множитель, частное — II сомножитель.
Следует отметить, что величина может делиться на другую с остатком и без него. Критерии делимости работают только для целочисленного деления. Это означает, что частным должно быть только целое число. Признаки делятся на девять основных правил-критериев. К ним относятся следующие:
Специалисты выделяют всего девять основных критериев делимости, на которых основаны правила для других чисел. Например, 14. На него делятся только величины, которые можно поделить без остатка на двойку и семерку.
Специалисты рекомендуют при изучении какой-либо темы по математике сразу придумывать сферы ее практического применения. В результате такого подхода стремление к обучению заметно возрастает. Далее необходимо на нескольких задачах разобрать признаки делимости чисел.
Практическое применение
Применение критериев делимости следует рассматривать на практике. Например, нужно выяснить возможность целочисленного деления 32341454 на 7. Решение задания выглядит следующим образом:
Можно рассмотреть другой пример деления этого же числа на 3. Реализация выглядит таким образом:
Специалисты рекомендуют еще разобрать несколько примеров самостоятельно. Для этого нужно придумать значения, а затем попытаться найти их целочисленные делители. После этого они рекомендуют переходить к алгоритму идентификации простого и составного чисел, поскольку знания для выполнения этой операции достаточно.
Методика «простое или сложное»
Для определения типа числа необходимо применить специальную методику. Она состоит из таких шагов:
Телом алгоритма является второй пункт, который представляет сложную структуру. Она состоит из совокупности критериев — признаков делимости одной величины на другую. Практическая реализация алгоритма «простое или составное» (как его называют некоторые математики) имеет следующий вид:
Следует отметить, что выполнение алгоритма прекращается после первого найденного множителя. Последний должен быть отличен от единицы и искомого значения.
Пример решения задачи
В математике встречается определенный тип задач, в которых необходимо найти все множители заданного числа. Например, требуется найти все делители величины 78541, исключив 1 и 78541. Решать задачу нужно по такому алгоритму:
Следовательно, число 78541 не имеет делителей и является простым. В том случае, когда они будут найдены, результат записывается в такой форме: 78541=<делитель1; делитель2; делитель3 и т. д. >.
Таким образом, идентификация простого или составного числа осуществляется при помощи специального алгоритма, который основан на применении правил признаков делимости одной величины на другую.
Простые и составные числа, определения, примеры, таблица простых чисел, решето Эратосфена
В статье рассматриваются понятия простых и составных чисел. Даются определения таких чисел с примерами. Приводим доказательство того, что количество простых чисел неограниченно и произведем запись в таблицу простых чисел при помощи метода Эратосфена. Будут приведены доказательства того, является ли число простым или составным.
Простые и составные числа – определения и примеры
Простые и составные числа относят к целым положительным. Они обязательно должны быть больше единицы. Делители также подразделяют на простые и составные. Чтобы понимать понятие составных чисел, необходимо предварительно изучить понятия делителей и кратных.
Составными числами называют целые числа, которые больше единицы и имеют хотя бы три положительных делителя.
Единица не является ни простым ни составным числом. Она имеет только один положительный делитель, поэтому отличается от всех других положительных чисел. Все целые положительные числа называют натуральными, то есть используемые при счете.
Простые числа – это натуральные числа, имеющие только два положительных делителя.
Составное число – это натуральное число, имеющее более двух положительных делителей.
Натуральные числа, которые не являются простыми, называют составными.
Таблица простых чисел
Для того, чтобы было проще использовать простые числа, необходимо использовать таблицу:
Рассмотрим теорему, которая объясняет последнее утверждение.
Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.
Простых чисел бесконечно много.
Видно, что может быть найдено любое простое число среди любого количества заданных простых чисел. Отсюда следует, что простых чисел бесконечно много.
Решето Эратосфена
Данный способ неудобный и долгий. Таблицу составить можно, но придется потратить большое количество времени. Необходимо использовать признаки делимости, которые ускорят процесс нахождения делителей.
Перейдем к формулировке теоремы.
Данное число простое или составное?
Перед решением необходимо выяснять, является ли число простым или составным. Зачастую используются признаки делимости. Рассмотрим это на ниже приведенных примере.
Доказать что число 898989898989898989 является составным.
Ответ: 11723 является составным числом.
Числа. Простые числа.
Натуральные числа, большие единицы и числа, которые не являются простыми, называют составными числами. Т.о., все натуральные числа делятся на 3 класса: единица (имеет 1 делитель), простые числа (имеют 2 делителя) и составные числа (имеют больше 2-х делителей).
Начало последовательности простых чисел выглядит так:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, …
Если представить натуральные числа как произведение простых, то это будет называться разложение на простые либо факторизация числа.
Самое большое простое число, которое известно.
Некоторые свойства простых чисел.
Допустим, p — простое, и p делит ab, тогда p делит a либо b.
Кольцо вычетов Zn будет называться полем только в случае, если n — простое.
Характеристика всех полей — это нуль либо простое число.
Когда G — конечная группа, у которой порядок |G| делят на p, значит, у G есть элемент порядка p (теорема Коши).
Натуральное p > 1 будет простым лишь в случае, если (p-1)! + 1 можно подулить на p (теорема Вильсона).
Когда n > 1 — натуральное, значит, есть простое p: n 1 — целые взаимно простые числа, содержит нескончаемое число простых чисел (Теорема Дирихле о простых числах в арифметической прогрессии).
Любое простое число, которое большее тройки, можно представить как 6k+1 либо 6k-1, где k — натуральное число. Исходя из этого, когда разность нескольких последовательных простых чисел (при k>1) одинаковая, значит, она точно делится на шесть — к примеру: 251-257-263-269; 199-211-223; 20183-20201-20219.
Теорема Грина-Тао. Есть бесконечные арифметические прогрессии, которые состоят из простых чисел.
Ни одно простое число нельзя представить как n 2k+1 +1, где n>1, k>0. Другими словами, число, которое предшествует простому, не может быть кубом либо более высокой нечётной степенью с основанием, которое больше единицы.
Есть многочлены, у которых множество неотрицательных значений при положительных значениях переменных совпадает с множеством простых чисел. Пример:
Простые числа – это натуральные числа, их можно разделить только на два значения: единицу и себя. К натуральным относят те, которые используются во время счета, поэтому должно выполняться требование, чтобы они были положительными и целыми. Делители также не должны быть отрицательными и дробными.
Они широко применяются в криптографии, когда необходимо закодировать важную информацию от посторонних глаз. Шифрование касается каждого человека, так как используется в создании электронной почты, банковских карт. Даже мобильная связь защищается кодами.
Кроме того, используются на системах, защищающих транспортные средства от угонщиков, создают преграду для атак вирусов и взломов компьютерных сайтов. При попытке продолжить разложение простых чисел или определить закономерность появления, возникают новые способы математических расчетов.
Математика предлагает начинать знакомиться с данными понятиями в средней школе, в 5 или в 6 классе.
Проверка на принадлежность к определенному множеству достаточно простая:
Простые числа можно делить только на 1 и на такое же число. Например 3 и 7 — простые числа, 3 делится на 1 и на 3, 7 делится на 1 и на 7.
Составные числа можно делить не только на себя и единицу. При этом не должно получаться остатка. Они делятся на одно или несколько значений. Например, 8 и 6 относят к составным. Восьмерка делится на 1, 2, 4, 8; шестерка – на 1, 2, 3 и 6.
Определение простых чисел позволяет исключить из их ряда единицу. Она характеризуется наличием только одного делителя, не являющегося отрицательным значением. Получить ее можно, используя только один способ, умножив саму на себя.
Простые двузначные числа определяются по внешнему виду:
Если оканчиваются четной цифрой, то точно являются составными. То же касается и значений, имеющих больше двух знаков.
Если на конце находится цифра 5, то она входит в число делителей.
Такие простые способы помогают легко классифицировать многозначные показатели.
Некоторые двузначные вводят в заблуждение с первого взгляда, если оканчиваются на единицу. Кажется, что разложить на множители их невозможно. Но есть исключения, например: 21, 81. Чем дальше, тем больше отклонений от этой закономерности.
Последовательность простых чисел
Есть целые алгоритмы, помогающие получать новое, ранее неизвестное значение.
Существуют таблицы, в которых собраны найденные числа, имеющие не больше двух делителей, например, до 200, 1000 или больше.
Последовательность можно продолжать бесконечно, начинается она так: 2, 3, 5, 7, 11, 13, 17, 19 и т. д.
Наименьшее и наибольшее простое число
Самым меньшим значением, делящимся на себя и 1, является 2. Это единственное простое значение, являющееся четным. Остальные всегда делятся на два, то есть получают третий делитель.
Простых чисел много и их количество стремится к бесконечности, потому узнать самое большое невозможно.
Нескончаемость ряда была доказана еще до нашей эры Евклидом. Он предложил перемножить все известные исследуемые значения и прибавить к ним единицу.
При его делении в любом случае будет оставаться остаток, то есть отнести к составным невозможно. Что противоречит тому факту, что были использованы все известные простые числа, в том числе и самое большое. Значит, предположение о конечности ряда является неверным.
В настоящее время известно значение, имеющее около 25 миллионов знаков. Оно относится к наибольшему из открытых наукой, это 2 82 589 933
Множество простых чисел
Множествами называются совокупности элементов, объединенных в одно целое общими свойствами.
Для изучаемых объектов к ним относятся:
принадлежность к натуральным;
наличие максимум двух делителей.
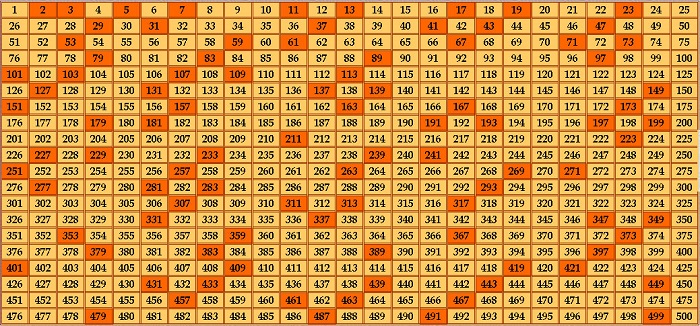
Простые числа можно определить, используя решето Эратосфена. Нужно выписать в ряд все значения, с которыми предстоит работать. Выбрать самое маленькое и вычеркнуть его, затем продолжать действие, убирая кратные ему.
Например, в ряду от 1 до 100 первым таким объектом будет 2. Поэтому и вычеркивать нужно значения, кратные двойке, то есть те, которые делятся на нее.
По окончании из оставшихся выбрать новое простое, искать кратные ему и также убирать. Повторять, пока это представляется возможным.
В итоге, все составные окажутся зачеркнутыми.
Эратосфен использовал свое открытие следующим образом. Он брал папирус, записывал на нем необходимые значения, при отборе прокалывал неподходящие острым предметом (отсюда название «решето Эратосфена»). Поэтому они как будто просеивались через сито, и в списке оставались видимыми только необходимые.
Некоторые свойства простых чисел
Выделяют свойства, объединенные в теоремы, постулаты. Многие являются основой математических правил, используемых в настоящее время.
Изучением занимается теория чисел, при использовании формул простые числа обозначаются буквой n.
Известны следующие правила:
Если рассматривать два простых числа (n), одно из которых делится на другое, то можно утверждать, что они равны.
Все являются нечетными, за исключением двойки.
Можно выделить пары, разница между которым равна 2. При их сложении получается значение, кратное трем. Их так и называют парными или близнецами. Исключение составляют две первые цифры в ряду, 3 и 5, так как сумму, полученную при их сложении, нельзя разделить на 3.
Для каждого натурального значения (N), большего единицы, существует n, превышающее его. При этом удвоенное натуральное будет больше n.
Если одно из двух N делится на n, то их произведение также будет делиться на него.
Любое N, за исключением единицы, можно отнести к n или представить в виде их произведения.
Если взять составное число и разложить его на множители n, то среди них окажется один, квадрат которого будет меньше первоначального составного.
Некоторые n имеют пары, которые можно найти, перевернув n наоборот. Например, 13 и 31, 37 и 73. То же самое касается трехзначных n: 107 и 701, 709 и 907.
Если N возвести в степень, представленную n, а затем вычесть N, то полученное значение будет делиться на используемое n. Это правило представляет собой малую теорему Ферма.
Действия с простыми числами
Можно использовать разные арифметические действия, складывать, умножать, вычитать, делить. Простые числа могут являться основанием и показателем степени.
Извлечь корень из них невозможно.