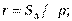Что значит произвольный треугольник
Что значит произвольный треугольник
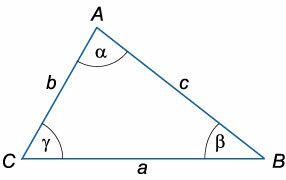
Треугольником называется геометрическая фигура, образованная тремя отрезками, соединяющими три точки, не лежащие на одной прямой.
Сумма углов треугольника равна \(180^\circ\):
\(\alpha + \beta + \gamma = 180^\circ\)
Неравенство треугольника
\(a + b > c\)
\(b + c > a\)
\(a + c > b\)
Радиус описанной окружности
\(R = \large\frac<<\sin \alpha >>\normalsize = \large\frac<<\sin \beta >>\normalsize = \large\frac
Нахождение высот треугольника по известной стороне и углу
\(
\(
\(
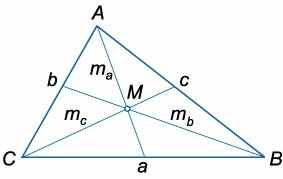
Расстояния от вершин до центра пересечения медиан
\(AM = \large\frac<2><3>\normalsize
Площадь треугольника
\(S = \large\frac<
\(S = \large\frac<
\(S = pr\)
\(S = \large\frac<
\(S = 2
\(S =
Треугольник
Рис. 1. Треугольник (общий случай)
Треугольник — замкнутая геометрическая фигура, состоящая из трёх отрезков (в общем случае, разных). В физике эти отрезки классически называются буквами латинского алфавита ( и т.д.), в отличие от обозначений в геометрии.
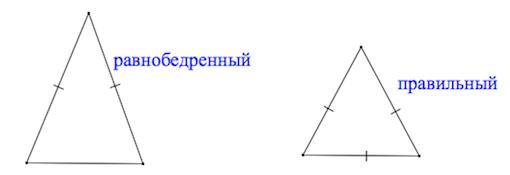
В случае, если у треугольника равны две стороны, данный треугольник называется равнобедренным.
В случае, если у треугольника все стороны одинаковы, он называется равносторонним.
В случае, если у треугольника один и углов прямой ( ), он называется прямоугольным.
Для произвольного треугольника вводят ряд отрезков, характеризующих треугольник и обладающих собственными свойствами:
Для разных типов треугольников поиск длин параметров треугольника может происходить по-разному. Для физических задач использование конкретной формулы диктуется конкретными данными задачи.
Рис. 2. Треугольник (биссектриса)
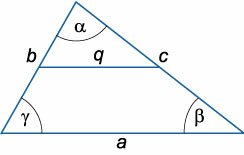
Биссектриса угла — геометрическое место точек, равноудалённых от сторон этого угла. Т.е. биссектриса — это линия, которая делит угол треугольника пополам (рис. 2). Известно, что биссектриса внутреннего угла треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам.
Для нахождения биссектрисы угла через различные данные можно пользоваться следующими соотношениями:
Медиана треугольника — отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны. Все медианы треугольника пересекаются в одной точке: данная точка делит медианы в соотношении 2 к 1, считая от вершины (рис. 3).
Рис. 3. Треугольник (медиана)
Для нахождения медианы треугольника через различные данные можно пользоваться следующими соотношениями:
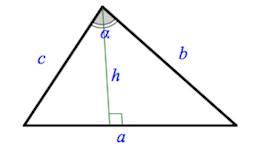
Рис. 4. Треугольник (высота)
Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или на её продолжение (рис. 4).
Для нахождения высоты треугольника через различные данные можно пользоваться следующими соотношениями:
Важно: то, какую формулу выбрать для решения конкретной задачи, зависит от того, что легче найти, исходя из дано.
Произвольный треугольник



R=a/(2sinα), где α — угол, противолежащий стороне a;
Радиус вписанной окружности: r=SΔ/p, где p — полупериметр.
105. Если все стороны четырёхугольника касаются окружности, то он называется четырёхугольником, описанным около этой окружности, а окружность — вписанной в четырёхугольник.
Не все четырёхугольники возможно описать около окружности, так как биссектрисы четырёх углов могут не пересекаться в одной точке, и не удастся найти центр вписанной окружности.
106. Если суммы противоположных сторон четырёхугольника равны, то в такой четырёхугольник можно вписать окружность.
Суммы противоположных сторон описанного четырёхугольника равны АД+ВС=АВ+СД
107. Четырёхугольник, все вершины которого лежат на окружности, называется вписанным в эту окружность, а окружность называется описанной около четырёхугольника.
Если сумма противоположных углов четырёхугольника равна 180°, то около него можно описать окружность.
108. Вектор можно обозначить:
— двумя заглавными буквами, поставив над ними стрелочку; первая буква показывает начальную точку, вторая — конечную точку, например, A¯B (читается: вектор AB);
— маленькой буквой со стрелочкой над ней, например, a⃗ (читается: вектор a).
Если начальная и конечная точки вектора совпадают, получается нулевой вектор, который обозначается как 0⃗. Любую точку на плоскости можно считать нулевым вектором.
Длина отрезка AB называется длиной, или модулем, вектора AB и обозначается так: ∣AB∣.
109. Скалярными называют величины, имеющие численное значение, но не имеющие направления.
Примеры — количество каких-нибудь предметов, длина, плотность.
110. Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление. Примеры векторных величин — скорость, сила, перемещение.
111. Перемещением движущейся точки в данный момент времени называют вектор с началом в точке начала её движения и концом в точке её расположения в этот момент.
Векторными величинами, или векторами, называют величины, имеющие и численное значение, и направление.
Например, если сказано, что автомобиль движется со скоростью 100 километров в час (то есть, дано численное значение скорости), то про его скорость известно не всё, потому что неизвестно, куда, в каком направлении он двигается. Поэтому примеры векторных величин — скорость, сила, перемещение.
112. Запомни различие между расстоянием и перемещением.
Расстояние характеризуется только числовым значением, например, AB+BC+CD=5 км.
Расстояние — скалярная величина.
Перемещение — вектор AD, соединяющий начальное и конечное положение тела, и его длина не равняется 5 км.
Перемещение — векторная величина.
Например, можно проехать 5 км и вернуться обратно, перемещение же в этом случае будет равно 0 и обозначится как нулевой вектор.
113. Два отличных от нуля вектора, которые находятся на одной прямой или параллельных прямых, называются коллинеарными векторами.
114. Два коллинеарных вектора могут быть направлены в одном направлении или в противоположных направлениях. В первом случае коллинеарные векторы называются сонаправленными, а во втором — противоположно направленными векторами.
115. Векторы с равными модулями и одинаковыми направлениями называются равными векторами.
116. Векторы с равными модулями и противоположными направлениями называются противоположными векторами.
Меняя направление какого-либо вектора на противоположное, получаем вектор, противоположный данному: AB=−BA
a⃗ +b⃗ =c⃗ Такой приём сложения векторов называется правилом треугольника.
Такой приём сложения векторов называется правилом параллелограмма.
120. Законы сложения векторов:
1) Для любых двух векторов a⃗ и b⃗ в силе равенство a⃗ +b⃗ =b⃗ +a⃗ (коммутативный, или переместительный, закон сложения).
121. Сумму нескольких векторов получаем так: складываем первый и второй вектор, затем к их сумме прибавляем третий вектор и т. д.
Из закона сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке они складываются. Это правило многоугольника.
122. Чтобы лучше понять закон вычитания векторов, нужно вспомнить свойство математических действий: сложения и вычитания.
Такое же свойство справедливо и для действий с векторами.
1) векторы нужно привести к общему началу A;
2) соединить конечные точки B и C;
3) отметить направление вектора разности от конечной точки уменьшителя к конечной точке уменьшаемого вектора.
— векторы a⃗ и b⃗ сонаправлены, если k>0;
— векторы a⃗ и b⃗ противоположно направлены, если k
ТРЕУГОЛЬНИК
в 







ma, mb, mc – медианы на соответствующие стороны. МВ:МД=МА:МЕ=МС:МК=2/1

r – радиус вписанной окружности. О – точка пересечения серединных перпендикуляров к сторонам треугольника (центр описанной окружности). Радиус описанной окружности:


высота опущенная на соответствующую сторону с. На всех 4–х нарисованных треугольниках стороны одинаково обозначены, просто на 1–м они обозначены, а на остальных они опущены для упрощения рисунка. И вообще подразумевается, что все 4 треугольника абсолютно одинаковые.
M 
ТЕОРЕМА СИНУСОВ






ПЛОЩАДЬ ТРЕУГОЛЬНИКА






Треугольник
Треугольник произвольный
Треугольник – это многоугольник с тремя сторонами (тремя углами).
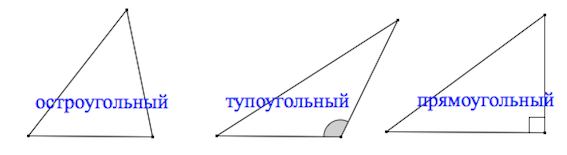
Виды треугольников :+ показать
Остроугольный треугольник – треугольник, у которого все углы острые (то есть меньше 90˚).
Тупоугольный треугольник – треугольник, у которого один из углов тупой (больше 90˚).
Прямоугольный треугольник – треугольник, у которого один из углов прямой (равен 90˚).
Равносторонний (правильный) треугольник – треугольник, у которого все три стороны равны.
Свойства
1. Против большей стороны лежит больший угол, и наоборот.
2. Против равных сторон лежат равные углы, и наоборот.
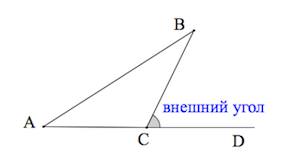
4. Внешний угол треугольника равен сумме внутренних углов,
не смежных с ним:
(Внешний угол образуется в результате продолжения одной из сторон треугольника).
5. Любая сторона треугольника меньше суммы двух других сторон.
Признаки равенства треугольников
1. Треугольники равны, если у них соответственно равны две стороны и угол между ними.
3. Треугольники равны, если у них соответственно равны три стороны.
Биссектриса, высота, медиана
Здесь подробно о биссектрисе, высоте, медиане треугольника.
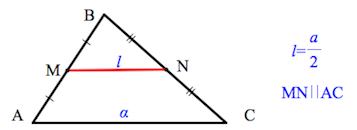
Средняя линия треугольника
Средняя линия треугольника – отрезок, соединяющий середины двух сторон треугольника.
Средняя линия треугольника параллельна третьей стороне и равна ее половине.
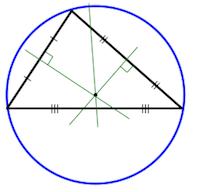
Вписанная окружность
Центр вписанной окружности – точка пересечения биссектрис треугольника.
Описанная окружность
Центр описанной окружности – точка пересечения серединных перпендикуляров.
Соотношение сторон в произвольном треугольнике
Теорема косинусов:
Теорема синусов:
Площадь треугольника
Через две стороны и угол между ними
Через радиус описанной окружности
Через радиус вписанной окружности
, где
– полупериметр
, где
– полупериметр
Смотрите также площадь треугольника здесь.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Есть пара ошибок в формулах. В частности в формуле вычисления площади через 2 стороны и угол между ними, в теореме Синусов, в разделе “свойства”.
А вообще отличные статьи, очень выручают, всё понятно и доступно, премного благодарен 😉
Анатолий, спасибо!
В разделе “свойства” ошибок не нашла…
В теореме синусов, – да… не пропечаталась буква гамма. Подправила.
В формуле площади треугольника, вы правы – картинка не соответствовала формуле. Исправила.
К сожалению, ошибки сразу не всегда замечаются.
Благодарю еще раз!
В разделе свойства:
Да, не хватало значка «» у А. Спасибо! 😉
Здраствуйте! Мне нужна ваша помощь!
Задача: ВЕРШИНЫ ТРЕУГОЛЬНИКА ДЕЛЯТ ОПИСАННУЮ ОКОЛО НЕГО ОКРУЖНОСТЬ НА ТРИ ДУГИ, ДЛИНЫ КОТОРЫХ ОТНОСЯТСЯ КАК 6:7:33. НАЙДИТЕ РАДИУС ОКРУЖНОСТИ, ЕСЛИ МЕНЬШАЯ ИЗ СТОРОН РАВНА 11.
Подозреваю, у вас опечатка в условии…
Если длины дуг (а значит и их градусные меры) находятся в отношении , то выходим на уравнение
Откуда
Значит угол треугольника, что напротив меньшей стороны, есть
Применяем теорему синусов: , откуда
спасибо я так и думал а то не могу решить и всё
СПАСИБО!
Здравствуйте. Пожалуйста, объясните, как решить задачу:
Вписанная в теругольник ABC окружность касается сторон AB, BC и AC в точках K,L и М соответственно.Найдите KL, если AM=2, МС=3 и угол С=π/3
Очевидно,
Примите за
.
Примените к треугольнику теорему косинусов:
Найдете , далее можно найти угол
и из треугольника
найти
Спасибо большое за ваш сайт. Очень радует, тот факт, что когда люди не понимают какую-нибудь задачу, вы помогаете решить. Спасибо. Побольше бы таких сайтов, всё понятно и доступно