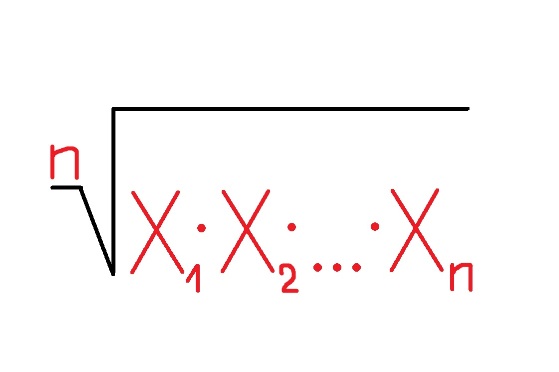Что значит проекция катета на гипотенузу
Что значит проекция катета на гипотенузу
Основные метрические сооьтношения в прямоугольном треугольнике
§1. Прямоугольный треугольник. Метрические соотношения.
Основные метрические сооьтношения в прямоугольном треугольнике
Пусть `ABC` прямоугольный треугольник с прямым углом `C` и острым углом при вершине `A`, равным `alpha` (рис. 1).
Используем обычные обозначения:
`a_c` и `b_c` – проекции `BD` и `AD` катетов на гипотенузу;
`h` – высота `CD`, опущенная на гипотенузу;
`m_c` – медиана `CM`, проведённая к гипотенузе;
`R` – радиус описанной окружности;
`r` – радиус вписанной окружности.
`sin alpha = a/c`, `cos alpha = b/c` и `»tg»alpha = a/b`.
Значения синуса, косинуса и тангенса острого угла прямоугольного треугольника зависят только от меры угла и не зависят от размеров и расположения треугольника.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
`c^2 = a^2 + b^2`
Доказательство теоремы повторите по учебнику.
Выведем ряд соотношений между элементами прямоугольного треугольника.
Квадрат катета равен произведению гипотенузы и его проекции на гипотенузу
Квадрат высоты, опущенной на гипотенузу, равен произведению проекции катетов на гипотенузу
Из треугольника `ACD` (рис. 1) имеем `»tg»alpha = (CD)/(AD)`, а из треугольника `BCD` `»tg»alpha = (BD)/(CD)`.
Значит `(BD)/(CD) = (CD)/(AD)`, откуда `CD^2 = AD * BD`, т. е. `h^2 = a_c * b_c`.
Произведение катетов равно произведению гипотенузы и высоты, опущенной на гипотенузу
Из треугольника `ABC` имеем `sin alpha = (BC)/(AB)`, а из треуольника `ACD` `sin alpha = (CD)/(AC)`.
Таким образом, `(BC)/(AB) = (CD)/(AC)`, откуда `BC * AC = AB * CD`, т. е. `a * b = c * h`.
Медиана, проведённая к гипотенузе, равна половине гипотенузы, т. е.
.
Полезно также запомнить, что медиана к гипотенузе разбивает треугольник на два равнобедренных треугольника.
Радиус окружности, описанной около прямоугольного треугольника, равен половине гипотенузы
Это следует из Свойства 4, действительно, `MA = MB = MC`, следовательно, окружность с центром в точке `M` и радиуса `c/2` проходит через три вершины.
Сумма катетов равна удвоенной сумме радиусов описанной и вписанной окружностей
`a + b = 2(R + r)` или `a + b = c + 2r`
Равенства, доказанные в Свойствах 1 и 2, записываются также как:
Как найти проекцию катета на гипотенузу
Если в исходных условиях задачи приведены длины гипотенузы (С) и того катета (А), проекцию которого (Ас) требуется вычислить, то используйте одно из свойств треугольника. Воспользуйтесь тем, что среднее геометрическое длин гипотенузы и искомой проекции равно длине катета: А = √(С*Ас). Так как понятие «среднее геометрическое» эквивалентно «корню из произведения», то для нахождения проекции катета возводите в квадрат длину катета и делите полученное значение на длину гипотенузы: Ас = (А/√С)² = А²/С.
Если длина гипотенузы неизвестна, а даны лишь длины обоих катетов (А и В), то в вычислении длины нужной проекции (Ас) можно задействовать теорему Пифагора. Выразите в соответствии с ней длину гипотенузы через длины катетов √(А²+В²) и подставьте полученное выражение в формулу из предыдущего шага: Ас = А²/√(А²+В²).
Если длины катетов неизвестны, но дано их соотношение (x/y), а также длина гипотенузы (C), то воспользуйтесь парой формул из первого и третьего шагов. Согласно выражению из первого шага, соотношение проекций катетов (Ас и Вс) будет равно соотношению квадратов их длин: Ас/Вс = x²/y². С другой стороны, согласно формуле из предыдущего шага, Ас+Вс = С. В первом равенстве выразите длину ненужной проекции через нужную и подставьте полученное значение во вторую формулу: Ас + Ас*x²/y² = Ас*(1 + x²/y²) = С. Из этого равенства выведите формулу нахождения нужной проекции катета: Ас = С/(1 + x²/y²).
Если известна длина проекции на гипотенузу одного катета (Вс), а длина самой гипотенузы не приведена в условиях, но дана высота (Н), проведенная из прямого угла треугольника, то этого тоже будет достаточно для вычисления длины проекции другого катета (Ас). Возведите высоту в квадрат и разделите на длину известной проекции: Ас = Н²/Вс.
Как найти проекцию катета на гипотенузу
Две короткие стороны прямоугольного треугольника называют катетами, а длинную – гипотенузой. Проекции коротких сторон на длинную делят гипотенузу на два отрезка различной длины. Если появляется надобность в вычислении величины одного из этих отрезков, то методы решения задачи целиком зависят от предлагаемого в условиях комплекта начальных данных.
Инструкция
3. Если вестима длина проекции одного из катетов (Вс) и длина гипотенузы (С), то метод нахождения длины проекции иного катета (Ас) явствен – примитивно отнимите от 2-й вестимой величины первую: Ас = С-Вс.
4. Если длины катетов неведомы, но дано их соотношение (x/y), а также длина гипотенузы (C), то воспользуйтесь парой формул из первого и третьего шагов. Согласно выражению из первого шага, соотношение проекций катетов (Ас и Вс) будет равно соотношению квадратов их длин: Ас/Вс = x?/y?. С иной стороны, согласно формуле из предыдущего шага, Ас+Вс = С. В первом равенстве выразите длину непотребной проекции через необходимую и подставьте полученное значение во вторую формулу: Ас + Ас*x?/y? = Ас*(1 + x?/y?) = С. Из этого равенства выведите формулу нахождения требуемой проекции катета: Ас = С/(1 + x?/y?).
5. Если вестима длина проекции на гипотенузу одного катета (Вс), а длина самой гипотенузы не приведена в условиях, но дана высота (Н), проведенная из прямого угла треугольника, то этого тоже будет довольно для вычисления длины проекции иного катета (Ас). Возведите высоту в квадрат и поделите на длину знаменитой проекции: Ас = Н?/Вс.
Совет 2: Как обнаружить гипотенузу треугольника
Инструкция
2. Если знаменит один из катетов и острый угол, то формула для нахождения гипотенузы будет зависеть от того, какой данный угол по отношению к знаменитому катету – прилежащий (расположенный вблизи катета) либо противолежащий (расположенный наоборот него.В случае прилежащего угла, гипотенуза равна отношению катета на косинус этого угла: с = a/cos?;E угол противолежащий, гипотенуза равна отношению катета на синус угла: с = a/sin?.
Видео по теме
Совет 3: Как обнаружить среднее геометрическое
Среднее геометрическое в совокупности применяется реже, чем арифметическое среднее, впрочем оно может быть благотворно при вычислении среднего значения показателей, изменяющихся с течением времени (заработная плата отдельного работника, динамика показателей успеваемости и т.п.).
Вам понадобится
Инструкция
1. Для того дабы обнаружить среднее геометрическое ряда чисел, для начала надобно перемножить все эти числа. Скажем, вам дан комплект из пяти показателей: 12, 3, 6, 9 и 4. Перемножим все эти числа: 12х3х6х9х4=7776.
2. Сейчас из полученного числа надобно извлечь корень степени, равной числу элементов ряда. В нашем случае из числа 7776 необходимо будет извлечь корень пятой степени при помощи инженерного калькулятора. Полученное позже этой операции число – в данном случае число 6 – будет являться средним геометрическим для начальной группы чисел.
3. Если у вас под рукой нет инженерного калькулятора, то вычислить среднее геометрическое ряда чисел дозволено с подмогой функции СРГЕОМ в программе Excel либо при помощи одного из онлайн-калькуляторов, намеренно предуготовленных для вычисления средних геометрических значений.
Обратите внимание!
Если понадобится обнаружить среднее геометрическое каждого для 2-х чисел, то инженерный калькулятор вам не потребуется: извлечь корень 2-й степени (квадратный корень) из всякого числа дозволено при помощи самого обыкновенного калькулятора.
Полезный совет
В различие от среднего арифметического, на геометрическое среднее не так крепко влияют крупные отклонения и колебания между отдельными значениями в исследуемом комплекте показателей.
Совет 4: Как обнаружить проекцию
В прямоугольном треугольнике существует два вида сторон – короткая сторона «катет» и длинная сторона «гипотенуза». Если провести проекцию катета на гипотенузу, та разделится на два отрезка. Дабы определить величину одного из них, надобно прописать комплект начальных данных.
Инструкция
2. Рассматривая, что корень из произведения обозначает то же самое, что и среднее геометрическое, возведите в квадрат значение N (длину желанного катета), и поделите на длину гипотенузы. То есть Nd = (N/?D)? = N?/D.В начальных данных задачи длина могут быть даны значения только катетов N и T. В этом случае длину проекции Nd находите с поддержкой теоремы Пифагора.
4. Если в начальных данных содержится информация о длине проекции катета Rd и величине гипотенузы D, то длину проекции второго катета Nd вычислите с подмогой примитивной формулы вычитания – Nd = D – Rd.
5. В обстановки, когда знаменито лишь значение длины гипотенузы D и дано примитивное соотношение длин катетов (m/h) обратитесь за поддержкой к формулам из первого шага и третьего шага.
6. Согласно формуле из первого шага примите как факт, что соотношение проекций Nd и Rd приравнивается к соотношению квадратных значений их длин. То есть Nd/Rd = m?/h?. Также сумма проекций катетов Nd и Rd равняется длине гипотенузы.
7. Выразите значение проекции катета Rd через желанный катет Nd и подставьте в формулу суммирования. В итоге вы получите Nd + Nd*m?/h? = Nd*(1 + m?/h?) = D, позже чего выведите формулу нахождения Nd = D/(1 + m?/h?). Значение Nd и укажет величину желанного катета.
Совет 5: Как вычислить длину катета прямоугольного треугольника
Треугольник именуется прямоугольным, если угол одной из его вершин равен 90°. Сторона, которая лежит наоборот этой вершины, именуется гипотенузой, а две другие – катетами. Длины сторон и величины углов в такой фигуре связаны между собой теми же соотношениями, что и в любом ином треугольнике, но потому что синус и косинус прямого угла равны единице и нулю, формулы гораздо упрощаются.
Инструкция
2. Зная величину угла (?) при вершине треугольника, лежащей наоборот катета знаменитой длины (a), тоже дозволено рассчитать неведомую длину второго катета (b). Для этого примените определение одной из тригонометрических функций – тангенса – для острого угла. Из него вытекает, что желанная длина катета должна быть равна размеру знаменитой стороны, поделенному на тангенс противолежащего угла: b = a/tg(?).
3. Определение котангенса для острого угла используйте для нахождения длины катета (b) в том случае, если в условиях приведена величина угла (?), примыкающего к иному катету вестимой длины (a). Формула в всеобщем виде будет выглядеть примерно так же, как и в предыдущем шаге, замените в ней лишь наименование функции и обозначение угла: b = a/ctg(?).
4. При вестимой длине гипотенузы (c) в вычислениях размеров катета (b) дозволено применять определения основных тригонометрических функций – синуса и косинуса – для острых углов. Если в условиях дана величина угла (?) между этими двумя сторонами, из 2-х функций следует предпочесть косинус. Умножьте длину гипотенузы на косинус знаменитого угла: b = c*cos(?).
5. Определение синуса для острых углов используйте в тех случаях, когда помимо длины гипотенузы (c) дана величина угла (?) в вершине, лежащей наоборот желанного катета (b). Формула расчета в всеобщем виде будет схожа с предыдущей – она должна содержать произведение длины гипотенузы на синус угла заданной величины: b = c*sin(?).