Что значит прочесть функцию
Построение графиков функций
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные курсы по математике для учеников с 1 по 11 классы!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:
Урок «Изучение графика числовых функций»
Краткое описание документа:
Каждый старший школьник должен уметь читать графики числовых функций. Такие навыки начинают отрабатываться с момента знакомства с графиками в курсе математики. К 10 классу эти умения должны получить достаточно устойчивый уровень. Хотя с самим понятием чтения графиков, в более глубоком смысле, обучающиеся знакомятся именно в 10 классе. И в помощь учителю, который собирается объяснять материал по данной теме, разработан данный видеоурок.
Здесь содержится полезная, полная и качественная информация, усвоение которой не затруднено ничем. Обучающиеся легко освоят материал по теме, так как он подобран в соответствии со рядом требований, в том числе по возрасту обучающихся.
Урок длится 5:32 минут. Практически столько же времени, если не отвлекаться на какие-то посторонние моменты, понадобится учителю, чтобы объяснить новый материал на уроке. Здесь же время строго регламентировано. Поэтому пока обучающиеся будут просматривать видеоурок, у них не будет времени отвлекаться, иначе они не поймут суть происходящего. Так с помощью данного урока можно сформировать у обучающихся такие качества, как внимательность, дисциплинированность и самостоятельность.
Автор урока обращает внимание слушателей на то, что чтение графиков числовых функций имеет широкое применение в нашей жизни. Особенно часто чтение графиков используется в экономике. При этом на экране изображен график некоторой функции.
Здесь же автор предлагает вспомнить, какая функция называется числовой. Пока обучающиеся начинают вспоминать, он напоминает им данное понятие. При этом объяснение сопровождается иллюстрацией. При этом, получается, что необходимо также вспомнить, что называется областью определения и областью значений функции. Автор напоминает и то, как выглядит уравнение функции в общем виде.
Чтобы обучающимся было проще понять принцип чтения графиков функций, необходимо вспомнить, что называется аргументом, то есть зависимой переменной, и независимой переменной. После этого предлагается рассмотреть некоторую произвольную функцию и построить ее график, подобрав пары чисел, которые являются координатами точек в системе координат. Когда график построен, вводится определение графика функции.
Далее автор говорит, что означает прочитать график функции. Получается, что для этого необходимо перечислить ее свойства, которые видны по графику. При этом перечисляются те свойства, которыми обладают все функции, и те, которыми обладают только некоторые функции.
Затем предлагается рассмотреть в качестве примеров, известные функции, которые были изучены в курсе алгебры ранее. Таких функций рассматривается две, последовательно. Сначала на экране изображается график функции, а затем подробно описывается каждое свойство, которым обладает функция. На каждом пункте автор останавливается и поясняет, что и как получается.
На этом видеоурок завершается, но не заканчивается занятие в школе. Поэтому оставшееся время желательно посвятить закреплению материала, подобрав для этого необходимые задания.
Урок будет полезен как для учителей, так и для обучающихся.
Чтение графика числовой функции.
Чтение графиков функций имеет большое практическое значение. В частности, использование функциональных зависимостей и построение графиков широко применяется в экономике.
Для изучения сегодняшней темы нам необходимо вспомнить: какая функция называется числовой?
Числовой функцией называется правило, с помощью которого каждому элементу из множества икс большое мы ставим в соответствие единственный элемент из множества игрек большое.
Множество Х называется областью определения функции.
Множество У называется множеством значений функции.
Равенство игрек равен эф от икс называется уравнением функции.
А что называется графиком функции?
Если дана функция игрек равно эф от х, где икс принадлежит икс большому и возьмем все пары икс, игрек и поставим им в соответствие соответствующие точки координатной плоскости, то получим график функции. График функции – это графической изображение зависимости между множествами икс большое и игрек большое.
1)область определения функции;
2)область значений функции;
3)нули функции – значения аргумента, при которых функция равна нулю;
4)промежутки знакопостоянства функции, т.е.промежутки,
где значения функции имеют один и тот же знак;
5)промежутки монотонности функции, т.е. промежутки, где функция возрастает или убывает;
6)наибольшееи наименьшее значения функции, т.е. самое большое и самое маленькое значение зависимого переменного;
Свойства, которые имеют не все функции:
9) четность, нечетность;
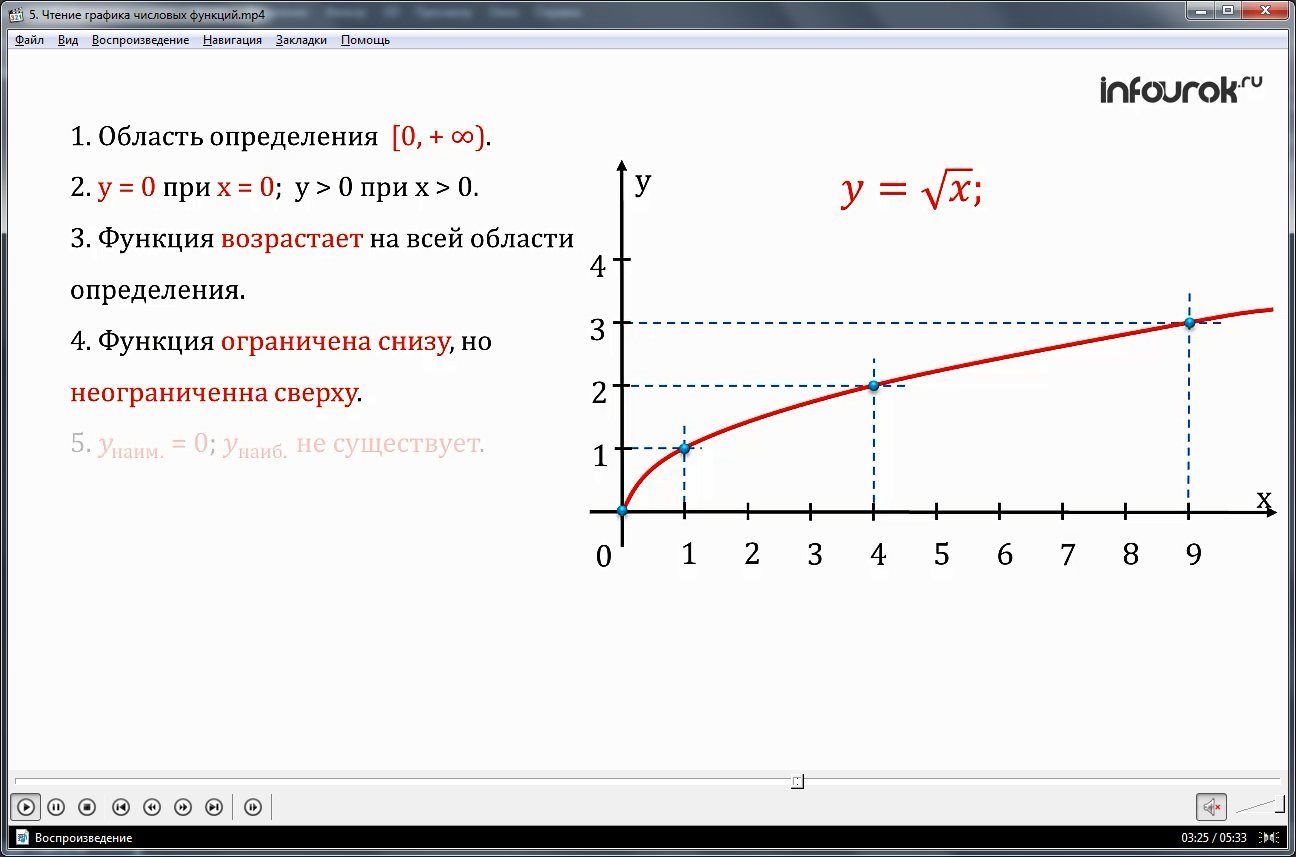
Прочитаем графики известных нам функций, например,игрек равен квадратный корень из икс.
1. Область определения функции —
луч от нуля до плюс бесконечности
2. Игрек равен нулю при икс равному нулю; игрек больше нуля при икс больше нуля.
3. Функция возрастает на всей области определения.
6.Функция непрерывна в заданной области определения.
7. Область значений функции — луч от нуля до плюс бесконечности
8.График обращен выпуклостью вверх.
у=кх+в
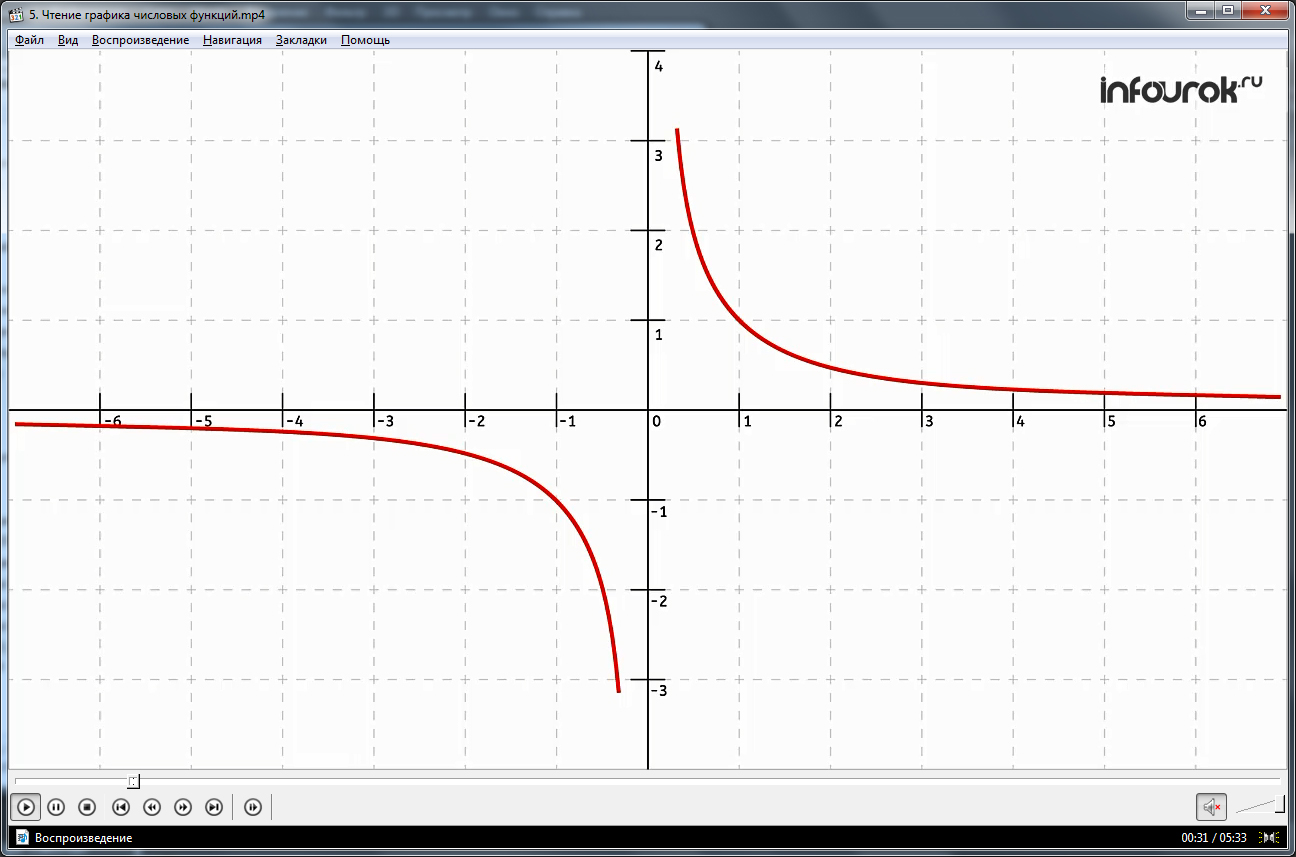
Прочитаем график ограниченной функции, график которой изображен
1.Область определения функции – отрезок от минус трех до трех.
7.Функция ограничена и сверху и снизу.
8.На отрезке минус трех до нуля функция выпукла вниз, а
на отрезке нуля до трех выпукла вверх.
9.Непрерывна на всей области определения.
Сегодня, мы научились читать графики элементарных функций. На следующем уроке мы продолжим чтение графиков тригонометрических функций, показательной, логарифмической.
Как читать графики на бирже
Графики — основа технического анализа при торговле на бирже. Они служат для визуальной оценки тенденций котировок конкретного инструмента, прогноза движения цены и анализа, чьи позиции сильнее — спроса или предложения. О том, как научиться читать графики на бирже, читайте в статье.
Возможности графиков и их комбинаций широко используются во время торговли как уже практикующими инвесторами, так и новичками. Естественно, среди доступных инструментов много тех, которые эффективны только для трейдеров с богатым опытом. Но существуют базовые виды, способные раскрыть информацию об активе без лишних сложностей.
Один из самых востребованных визуальных помощников на биржевом рынке — график движения цен. Выделяют несколько его видов.
Линейные графики. Наиболее простое изображение движения цены, но при этом отражающее только один компонент, которого недостаточно для принятия решений. Бары. Иногда их ещё называют столбиковыми графиками. Информативный визуальный вариант, в котором обозначены главные интересующие показатели — минимальный и максимальный уровень цен за выбранный период времени, цены закрытия и открытия. Японские свечи. Востребованный инструмент, отражающий те же параметры, что и бары, но визуализация у них удобнее. Пункто-цифровой. Другое название — крестики-нолики. Это столбики изменения цены, при этом нолик — падение уровня на заданное количество пунктов, крестик — рост на аналогичное значение. Отчётливо прослеживается направление движения котировки и величина скачка, но при этом нет привязки ко времени. Гистограммы. Не используются отдельно, а дополняют другие графики, показывая объём совершённых торгов. Чем больше высота линий, тем активнее оборот актива на рынке.
Навык чтения графиков — база, необходимая для успешного трейдинга. В техническом анализе наиболее востребованы среди трейдеров линейные, бары и свечные графики. Рассмотрим каждый из них подробнее.
Этот вид графика наиболее простой — по осям времени и цены строится линия, которая отражает величину котировки, закрывающей торговый период. По нему отслеживают общий тренд — растут активы в цене или падают, но принять решение без изучения дополнительной информации нельзя. Оптимальные таймфреймы — от одного дня до квартала.
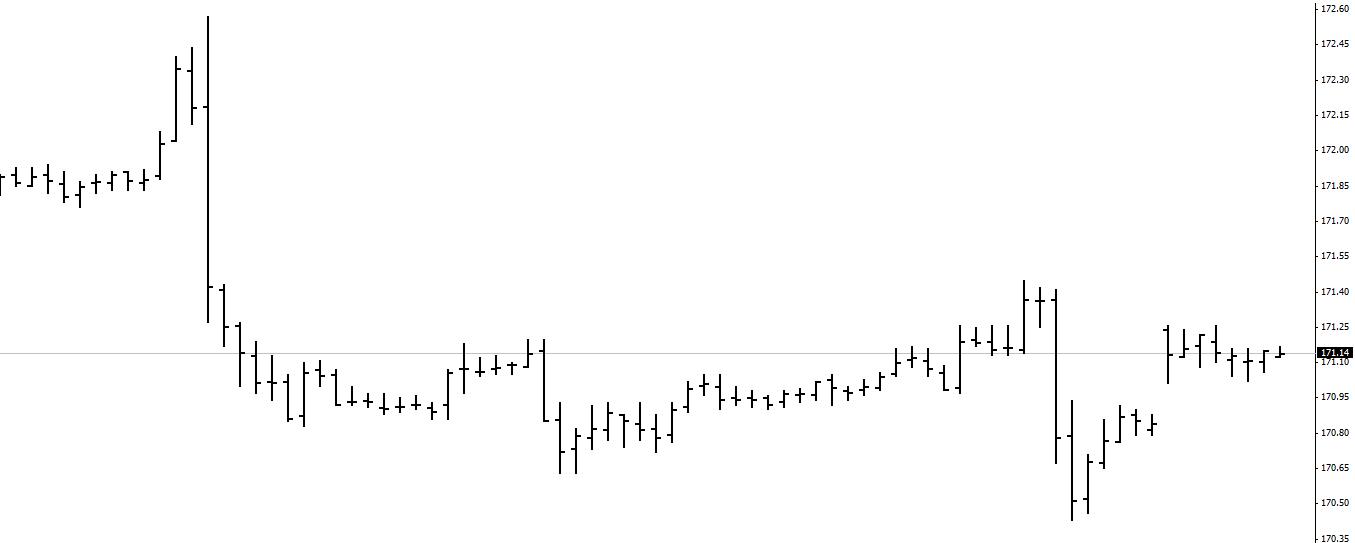
Бары популярны у западных трейдеров. Намного информативнее линейных графиков — посмотреть можно не только цену закрытия, но и открытия, максимальную и минимальную за период торгов.
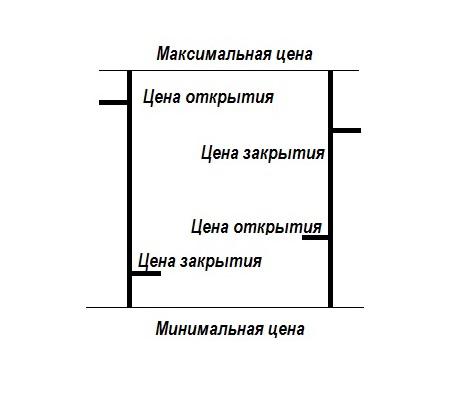
Внешний вид графика — вертикальные столбики с засечками. Границы — это значения минимума и максимума котировки. Засечка слева — цена открытия, засечка справа — цена закрытия. Просмотреть точные цифры можно, наведя курсор мыши на интересующую часть графика.
Каждый столбик — колебания котировки за выбранный таймфрейм. Это может быть пять минут, один час, один день. По окончании очередного периода формируется новая линия. Расположение засечек говорит о направлении движения цены: если левая выше правой, идёт падение, если наоборот — рост.
Такие графики также позволяют понять общую тенденцию и спрогнозировать разворот цены. Например, в ожидании экономических или политических новостей диапазон колебаний котировки уменьшается — столбики становятся короче, рынок замирает. Значимое увеличение длины столбца в сторону минимума или максимума от засечки сигнализирует о возможном развороте движения стоимости в противоположную сторону.
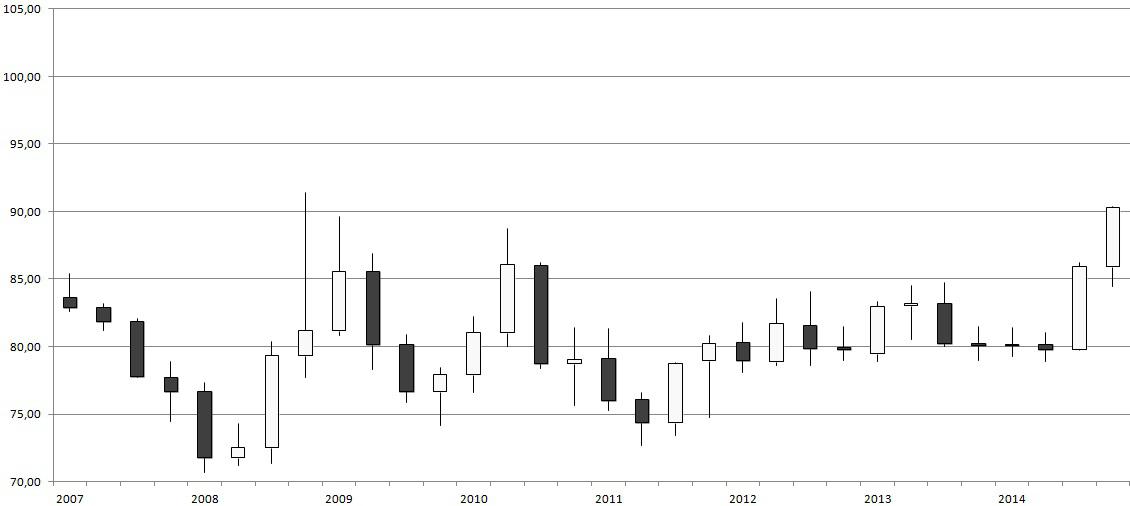
Большинство трейдеров на бирже использует график японские свечи. Он проверен временем — впервые свечные графики стали использовать торговцы при продаже риса ещё в XVII веке. За три сотни лет поклонники появились во всём мире, и их число только растёт.
График состоит из прямоугольников с хвостиками — тела свечи и её тени. Каждый отдельный элемент — это колебания котировки за определённый период времени. Таймфрейм устанавливает пользователь в настройках. Как и в случае с барами, с началом нового промежутка формируется очередная свеча.
Для анализа доступны данные аналогичные барам. Но визуально свечи воспринимаются легче из-за контрастного окрашивания их тел в случае роста и падения цены. В базовом варианте чёрный цвет — стоимость котировки убывает, белый — растёт. Трейдер может выбрать другие оттенки, перейдя в настройки торгового терминала.
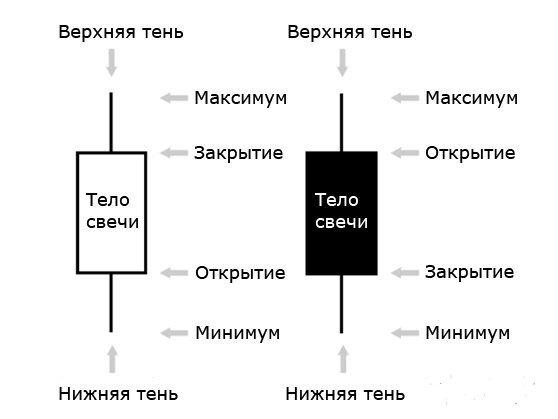
Чтобы разобраться, как читать свечной график на бирже, необходимо познакомиться с каждым элементом. Доступные для анализа параметры имеют собственные обозначения:
open (О) — цена открытия; close © — цена закрытия; low (L) — минимальное значение котировки; high (H) — максимальное значение котировки.
В зависимости от уровня колебаний тело свечи и её тени могут быть разными. Каждая модель носит своё название, например, «молот», «надгробие», «утренняя звезда», и несёт в себе определённый сигнал о ситуации на рынке. Их используют для прогнозирования двух важных состояний торгов:
Чаще всего удлинение тени свечи в сторону минимума характерно для поворота цены в направлении роста, соответственно, увеличение тени в сторону максимума говорит об обратной ситуации.
В любом инструменте есть свои положительные и отрицательные моменты. Предлагаем сравнить основные характеристики базовых графиков в таблице.