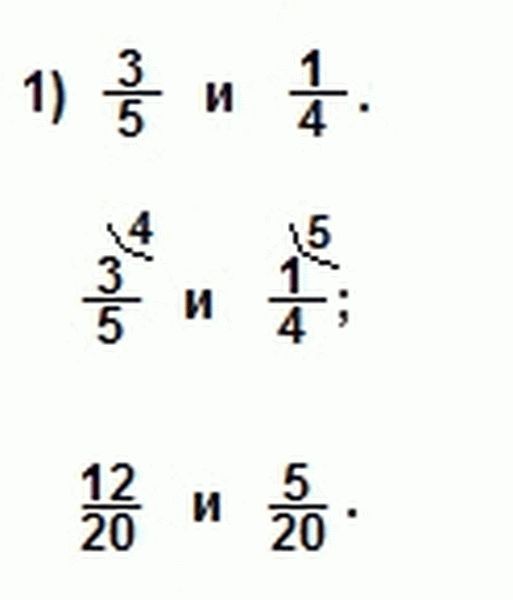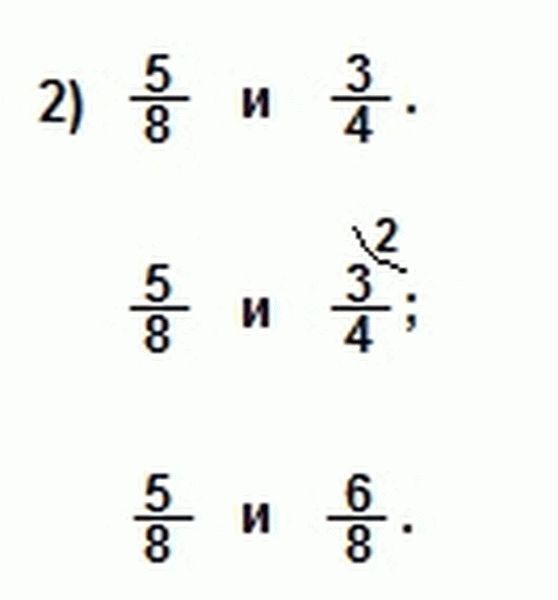Что значит привести дроби к наименьшему общему знаменателю
Как привести дроби к наименьшему общему знаменателю
Чтобы привести несколько дробей к наименьшему общему знаменателю, надо:
1) найти наименьшее общее кратное знаменателей этих дробей, оно и будет их наименьшим общим знаменателем;
2) разделить наименьший общий знаменатель на знаменатели данных дробей, т.е. найти для каждой дроби дополнительный множитель;
3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Пример: приведем к наименьшему общему знаменателю дроби 3/4 и 5/6.
1) Находим наименьшее общее кратное (НОК) чисел 4 и 6. Это 12. То есть 12 – минимальное число, на которое делятся без остатка и 4, и 6.
2) Делим 12 на знаменатель каждой из двух дробей, чтобы найти их дополнительные множители:
Таким образом, дополнительным множителем дроби 3/4 является 3, дроби 5/6 – 2.
3) Чтобы в знаменателе обеих дробей было число 12, надо умножить их числители и знаменатели на их дополнительные множители.
Нашли общий знаменатель двух дробей – число 12.
В дроби 3/4 делим 12 на знаменатель 4 и полученный результат умножаем на числитель 3:
Мы получили числитель. Итак, в числителе у нас 9, в знаменателе 12:
В дроби 5/6 делим 12 на 6 и полученный результат умножаем на 5:
Как привести дроби к наименьшему общему знаменателю
Наименьшим общим знаменателем (НОЗ) данных несократимых дробей является наименьшее общее кратное (НОК) знаменателей этих дробей. (см. тему «Нахождение наименьшего общего кратного»: 5.3.5. Нахождение наименьшего общего кратного (НОК) данных чисел ).
Чтобы привести дроби к наименьшему общему знаменателю, надо: 1) найти наименьшее общее кратное знаменателей данных дробей, оно и будет наименьшим общим знаменателем. 2) найти для каждой из дробей дополнительный множитель, для чего делить новый знаменатель на знаменатель каждой дроби. 3) умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Примеры. Привести следующие дроби к наименьшему общему знаменателю.
Находим наименьшее общее кратное знаменателей: НОК(5; 4)=20, так как 20 — самое меньшее число, которое делится и на 5 и на 4. Находим для 1-й дроби дополнительный множитель 4 (20:5=4). Для 2-й дроби дополнительный множитель равен 5 (20:4=5). Умножаем числитель и знаменатель 1-й дроби на 4, а числитель и знаменатель 2-й дроби на 5. Мы привели данные дроби к наименьшему общему знаменателю (20).
Наименьший общий знаменатель этих дробей — число 8, так как 8 делится на 4 и на само себя. Дополнительного множителя к 1-й дроби не будет (или можно сказать, что он равен единице), ко 2-й дроби дополнительный множитель равен 2 (8:4=2). Умножаем числитель и знаменатель 2-й дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (8).
Данные дроби не являются несократимыми.
Сократим 1-ю дробь на 4, а 2-ю дробь сократим на 2. (см. примеры на сокращение обыкновенных дробей: Карта сайта → 5.4.2. Примеры сокращения обыкновенных дробей ). Находим НОК(16; 20)=2 4 ·5=16·5=80. Дополнительный множитель для 1-й дроби равен 5 (80:16=5). Дополнительный множитель для 2-й дроби равен 4 (80:20=4). Умножаем числитель и знаменатель 1-й дроби на 5, а числитель и знаменатель 2-й дроби на 4. Мы привели данные дроби к наименьшему общему знаменателю (80).
Находим наименьший общий знаменатель НОЗ(5; 6 и 15)=НОК(5; 6 и 15)=30. Дополнительный множитель к 1-й дроби равен 6 (30:5=6), дополнительный множитель ко 2-й дроби равен 5 (30:6=5), дополнительный множитель к 3-ей дроби равен 2 (30:15=2). Умножаем числитель и знаменатель 1-й дроби на 6, числитель и знаменатель 2-й дроби на 5, числитель и знаменатель 3-ей дроби на 2. Мы привели данные дроби к наименьшему общему знаменателю (30).
Приведение дробей к наименьшему общему знаменателю
Дроби могут иметь множество общих знаменателей.
Могут иметь общие знаменатели: 4, 8, 12, 16 и т.д.:
В множестве чисел, являющихся общим знаменателем данных дробей существует наименьшее натуральное число, которое называют наименьшим общим знаменателем.
Таким образом, из всех общих знаменателей 4, 8, 12, 16 дробей:
наименьшим общим знаменателем будет знаменатель 4, так как число 4 – наименьшее натуральное число из чисел 4, 8, 12, 16.
Определение наименьшего общего знаменателя
Наименьший общий знаменатель – это наименьшее число из всех общих знаменателей данных дробей.
Наименьший общий знаменатель будет равен 36.
Чтобы найти наименьший общий знаменатель дробей, нужно найти наименьшее общее кратное (НОК) этих знаменателей.
Как привести дроби к наименьшему общему знаменателю
Шаг 1
Найти наименьший общий знаменатель.
Шаг 2
Найти дополнительный множитель.
Шаг 3
Умножить числитель и знаменатель каждой дроби на ее дополнительный множитель.
Шаг 4
Записать полученные дроби с новым знаменателем.
Пример 1
Привести дроби к общему знаменателю и наименьшему общему знаменателю::
Действие 1
Найдем общий знаменатель для рассматриваемых дробей.
Чтобы найти общий знаменатель, перемножим знаменатели:
Дополнительный множитель к первой дроби:
Дополнительный множитель ко второй дроби:
Дополнительный множитель к третьей дроби:
Запишем полученные дроби с общим знаменателем:
Действие 2
Приведем дроби к наименьшему общему знаменателю:
Чтобы привести дроби к наименьшему общему знаменателю нужно:
Шаг 1
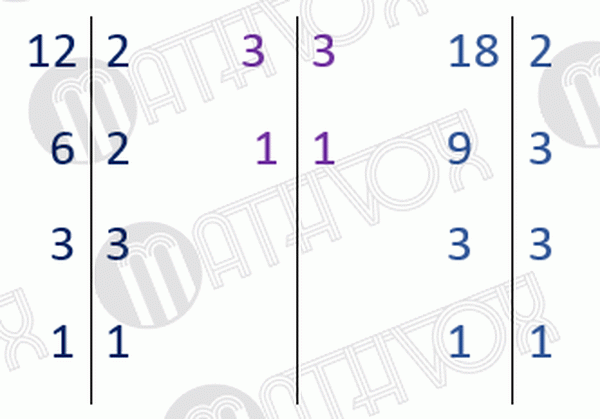
Чтобы найти наименьшее общее кратное (НОК) нужно знаменатели дробей разложить на множители.
Разложим их знаменатели на множители:
Запишем знаменатели как произведение множителей:
Из одинаковых простых множителей выберем тот множитель, который стоит в наибольшей степени, т. е.:
Наименьший общий знаменатель у этих дробей: 36.
Шаг 2
Находим дополнительные множители для этих дробей. Для этого 36 делим на 12, 3, 18 (знаменатели этих дробей):
Шаг 3
Умножим числители и знаменатели этих дробей на дополнительные множители:
Таким образом эти дроби привели к наименьшему общему знаменателю.
Ответ
приведенные к общему знаменателю:
приведенные к наименьшему общему знаменателю:
Пример 2
Привести к наименьшему общему знаменателю дроби:
Решение
Шаг 1
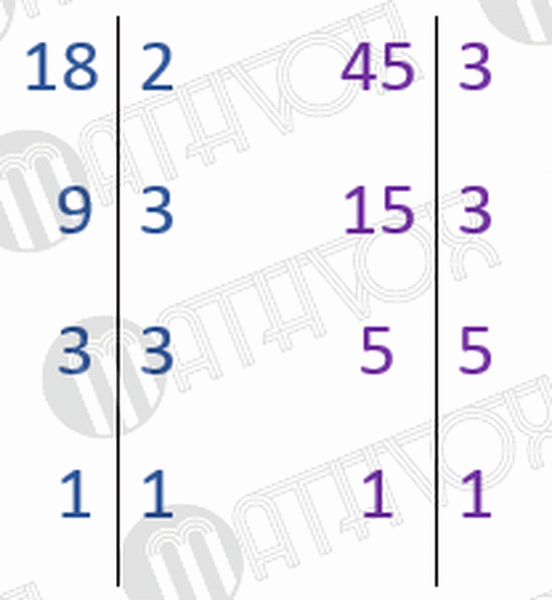
Найдем наименьший общий знаменатель. Для этого определим НОК. Чтобы найти НОК, разложим знаменатели на простые множители.
Представим знаменатели в виде произведения множителей:
Из одинаковых простых множителей выберем тот множитель, который стоит в наибольшей степени, т. е.:
Наименьший общий знаменатель 90.
Шаг 2
Найдем дополнительные множители для этих дробей. Для этого 90 делим на 18, 45 (знаменатели этих дробей):
Шаг 3
Умножим числители и знаменатели этих дробей на дополнительные множители:
Таким образом эти дроби привели к наименьшему общему знаменателю.
Ответ
приведенные к наименьшему общему знаменателю имеют вид:
Как привести дробь к НОЗ
Чтобы можно было выполнять операции сложения, вычитания и сравнения между простыми дробями, у них должны быть одинаковые знаменатели.
Если знаменатели дробей различны (именно так чаще и бывает), дроби следует привести к общему знаменателю.
Общим знаменателем называют число, кратное каждому из первоначальных знаменателей исходных дробей.
Наименьшим общим знаменателем (НОЗ) называют наименьший из всех возможных знаменателей или наименьшее общее кратное знаменателей исходных дробей.
Правило приведения двух дробей к НОЗ:
ПРИМЕР: Найти НОЗ дробей 18/81 и 13/45.
Дополнительный множитель для дроби 18/81 будет равен 5; для дроби 13/45 равен 9.
Умножаем числитель и знаменатель первой дроби на 5, а второй — на 9, после чего получаем две дроби с одинаковыми знаменателями: 90/405 и 117/405.
Задача 1: Что больше 14/19 или 27/33.
Приведение дробей к общему знаменателю.
Общий знаменатель и дополнительный множитель.
У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:
Пример разных знаменателей у дробей:
Как привести к общему знаменателю дроби?
У первой дроби знаменатель равен 3, у второй равен 13. Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.
Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.
Вторую дробь умножаем на дополнительный множитель 3.
Мы привели к общему знаменателю дроби:
Наименьший общий знаменатель.
Рассмотрим еще пример:
Приведем дроби \(\frac<5><8>\) и \(\frac<7><12>\) к общему знаменателю.
Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.
Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.
Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.
Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.
Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ сократить.
Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.
Например:
Приведите дроби \(\frac<1><4>\) и \(\frac<9><16>\) к наименьшему общему знаменателю.
Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:
Вопросы по теме:
Любые ли две дроби можно привести к одному общему знаменателю?
Ответ: да.
К какому знаменателю принято приводить дроби?
Ответ: к наименьшему общему знаменателю.
Пример №1:
Для дроби \(\frac<1><2>\) запишите равную дробь со знаменателем: а) 12 б) 18 в) 50?
Решение:
а) Число 2 нужно умножить на 6, чтобы получить 12. Следовательно, мы всю дробь умножаем на дополнительный множитель 6.
б) Число 2 нужно умножить на 9, чтобы получить 18. Следовательно, мы всю дробь умножаем на дополнительный множитель 9.
в) Число 2 нужно умножить на 25, чтобы получить 50. Следовательно мы всю дробь умножаем на дополнительный множитель 25.
Общий знаменатель, понятие и определение.
Так для чего нужен общий знаменатель, или когда нужен общий знаменатель?
Ответ довольно прост, мы имеем право дроби складывать и вычитать только когда у данных дробей есть общий знаменатель. Поэтому важно понять, как находить общий знаменатель.
Определение:
Общий знаменатель – это число всегда положительное на которое делятся знаменатели данных дробей.
Формула основного свойства рациональных чисел.
Такое решение называется приведением к общему знаменателю. Мы имеем право умножать одновременно на одно и тоже число и числитель и знаменатель.
Наименьший общий знаменатель.
Что такое наименьший общий знаменатель?
Определение:
Наименьший общий знаменатель – это наименьшее положительное число кратное знаменателям данных дробей.
Как привести к наименьшему общему знаменателю? Чтобы ответить на этот вопрос рассмотрим пример:
Решение:
Чтобы найти наименьший общий знаменатель нужно найти наименьшее общее кратное (НОК) знаменателей этих дробей.
У первой дроби знаменатель равен 20 разложим его на простые множители.
20=2⋅5⋅2
Так же разложим и второй знаменатель дроби 14 на простые множители.
14=7⋅2
Ответ: наименьший общий знаменатель будет равен 140.
Как привести дробь к общему знаменателю?
Нужно первую дробь \(\frac<1><20>\) домножить на 7, чтобы получить знаменатель 140.
Правила или алгоритм приведения дробей к общему знаменателю.
Алгоритм приведения дробей к наименьшему общему знаменателю:
Общий знаменатель для нескольких дробей.
Как найти общий знаменатель для нескольких дробей?
Рассмотрим пример:
Найдите наименьший общий знаменатель для дробей \(\frac<2><11>, \frac<1><15>, \frac<3><22>\)
Решение:
Разложим знаменатели 11, 15 и 22 на простые множители.
Число 11 оно само по себе уже простое число, поэтому его расписывать не нужно.
Разложим число 15=5⋅3
Разложим число 22=11⋅2
Найдем наименьшее общее кратное (НОК) знаменателей 11, 15, и 22.
НОК(11, 15, 22)=11⋅2⋅5⋅3=330
Мы нашли наименьший общий знаменатель для данных дробей. Теперь приведем данные дроби \(\frac<2><11>, \frac<1><15>, \frac<3><22>\) к общему знаменатели равному 330.
Вопросы по теме:
Какой общий знаменатель у дробей \(\bf \frac<2><25>\) и \(\bf \frac<1><14>\)?
Ответ:
Какой наименьший общий знаменатель у дробей 14 и 25? Воспользуемся алгоритмом приведения дробей к общему знаменателю алгебраических дробей.
Сначала разложим на простые множители знаменатели 14 и 25.
14=2⋅7
25=5⋅5
Теперь найдем НОК(14,25)=2⋅7⋅5⋅5=350.
Это мы нашли наименьший общий знаменатель:
Но не всегда нужно находит наименьший общий знаменатель иногда, можно найти любой знаменатель, а потом можно конечную дробь сократить. Например, для дробей \(\frac<2><25>\) и \(\frac<1><14>\) знаменателем может быть число 700, 1400 и т.д.
Приведение дробей к общему знаменателю
Общий знаменатель обыкновенных дробей
Если обыкновенные дроби имеют одинаковые знаменатели, то про эти дроби говорят, что они имеют общий знаменатель. Например, дроби

имеют общий знаменатель 7.
Общий знаменатель — это число, которое является знаменателем для двух и более обыкновенных дробей.
Дроби, имеющие разные знаменатели, можно привести к общему знаменателю.
Приведение дробей к общему знаменателю
Приведение дробей к общему знаменателю — это замена данных дробей, имеющих разные знаменатели, на равные им дроби, у которых одинаковые знаменатели.
Дроби можно привести либо просто к общему знаменателю, либо к наименьшему общему знаменателю.
Наименьший общий знаменатель — это наименьшее общее кратное знаменателей данных дробей. Чтобы привести дроби к наименьшему общему знаменателю нужно:
Пример. Привести к общему знаменателю дроби 

24 : 8 = 3 (для 
24 : 12 = 2 (для 
Приведение к общему знаменателю можно записывать в более краткой форме, указывая дополнительный множитель рядом с числителем каждой дроби (сверху справа или сверху слева) и не записывая промежуточные вычисления:
К общему знаменателю можно привести и более простым способом, умножив члены первой дроби на знаменатель второй дроби, а члены второй дроби — на знаменатель первой.
Пример. Привести к общему знаменателю дроби 

В качестве общего знаменателя дробей можно взять произведение их знаменателей.
Приведение дробей к общему знаменателю используется при сложении, вычитании и сравнении дробей, у которых разные знаменатели.
Калькулятор приведения к общему знаменателю
Дроби. Приведение дробей к общему знаменателю.
Любые 2 дроби возможно привести к одинаковому знаменателю, либо, говоря другими словами, к общему знаменателю. Приведение дробей к общему знаменателю значит выразить дроби в одинаковых частях единицы с сохранением величины дроби.
Общим знаменателем дробей может стать каждое общее кратное знаменателей этих дробей (пример: произведение знаменателей). Он равен наименьшему общему кратному (НОК) знаменателей этих дробей. Дробь не изменится, если ее числитель и знаменатель умножать на одинаковое число, не равное нулю.
Зачем приводят дроби к общему знаменателю? Ниже приведены некоторые причины:
Чтобы привести дроби к общему знаменателю, необходимо:
Привести дроби 

1. Определим наименьшее общее кратное (НОК) знаменателей заданных дробей – это будет искомым наименьшим общим знаменателем:
НОЗ (наименьший общий знаменатель) = 12;
2. Разделим наименьший общий знаменатель на знаменатели заданных дробей, то есть найдем для каждой дроби дополнительный множитель:
дополнительный множитель для дроби 
дополнительный множитель для дроби 
3. Умножим числитель и знаменатель каждой дроби на дополнительный множитель:

Дроби приведены к общему знаменателю.