Что значит правильная четырехугольная призма

Призма и ее элементы. Свойства правильной четырехугольной призмы

Призма является достаточно простой геометрической объемной фигурой. Тем не менее у некоторых школьников при определении ее основных свойств возникают проблемы, причина которых, как правило, связана с неправильно используемой терминологией. В данной статье рассмотрим, какие призмы бывают, как они называются, а также подробно охарактеризуем правильную четырехугольную призму.

Призма в геометрии

Вам будет интересно: Холю и лелею. Что значит лелеять и холить?

Элементы призмы и теорема Эйлера

Поскольку рассматриваемая объемная фигура представляет собой полиэдр, то есть образована набором пересекающихся плоскостей, то она характеризуется некоторым количеством вершин, ребер и граней. Все они являются элементами призмы.

В середине XVIII века швейцарский математик Леонард Эйлер установил связь между количеством основных элементов полиэдра. Эта связь записывается следующей простой формулой:

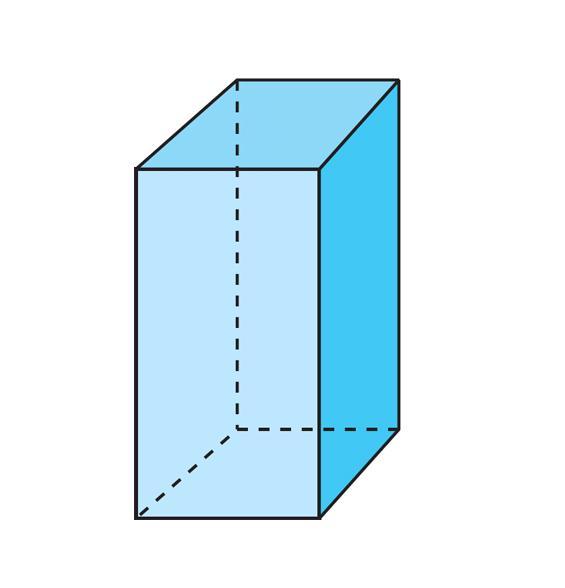
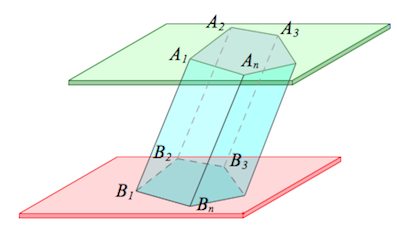
Для любой призмы справедливо это равенство. Приведем пример его использования. Предположим, имеется правильная четырехугольная призма. Она изображена на рисунке ниже.

Видно, что число вершин для нее равно 8 (по 4 для каждого четырехугольного основания). Число сторон, или граней составляет 6 (2 основания и 4 боковых прямоугольника). Тогда количество ребер для нее будет равно:

Все их можно посчитать, если обратится к тому же рисунку. Восемь ребер лежат в основаниях, а четыре ребра перпендикулярны этим основаниям.

Полная классификация призм

С этой классификацией важно разобраться, чтобы впоследствии не путаться в терминологии и использовать правильные формулы для вычисления, например, площади поверхности или объема фигур.

Для любой призмы произвольной формы можно выделить 4 признака, которые ее будут характеризовать. Перечислим их:

Из всех этих пунктов хотелось бы остановиться подробнее на последнем. Прямая призма также называется прямоугольной. Связано это с тем, что для нее параллелограммы являются прямоугольниками в общем случае (в некоторых случаях они могут быть квадратами).

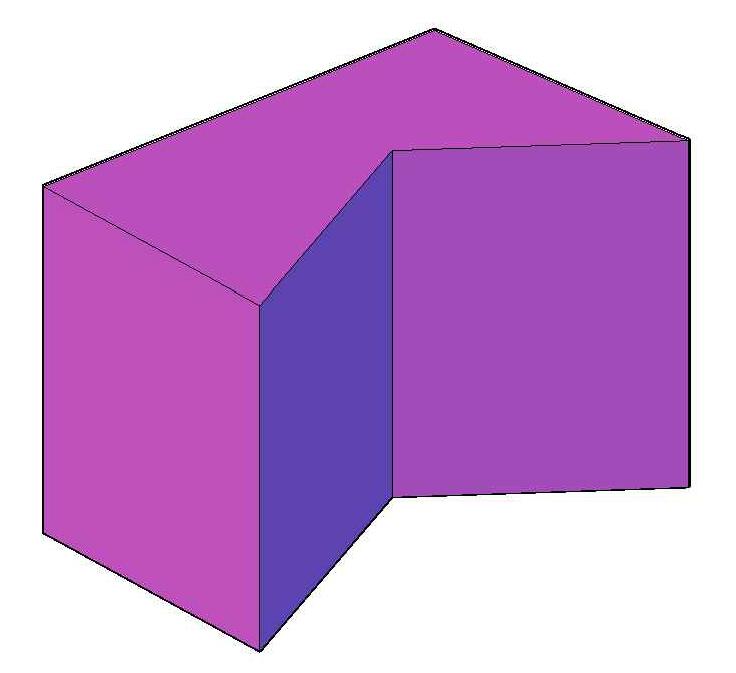
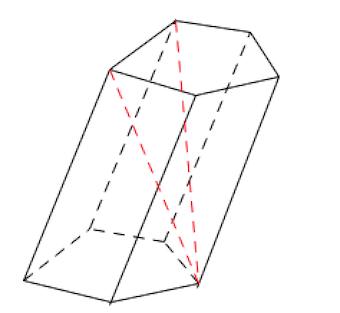
Для примера на рисунке выше изображена пятиугольная вогнутая прямоугольная, или прямая фигура.

Правильная четырехугольная призма

Основание этой призмы представляет собой правильный четырехугольник, то есть квадрат. Выше на рисунке уже было показано, как выглядит эта призма. Помимо двух квадратов, которые ее ограничивают сверху и снизу, она также включает 4 прямоугольника.

Обозначим сторону основания правильной четырехугольной призмы буквой a, длину ее бокового ребра обозначим буквой c. Эта длина также является высотой фигуры. Тогда площадь всей поверхности этой призмы выразится формулой:

S = 2*a2 + 4*a*c = 2*a*(a + 2*c)

Учитывая введенные обозначения для длин сторон, запишем формулу для объема рассматриваемой фигуры:

То есть объем вычисляется как произведение площади квадратного основания на длину бокового ребра.

Фигура куб

Все знают эту идеальную объемную фигуру, но мало кто задумывался, что она представляет собой правильную четырехугольную призму, сторона которой равна длине стороны квадратного основания, то есть c = a.

Для куба формулы полной площади поверхности и объема примут вид:

Источник

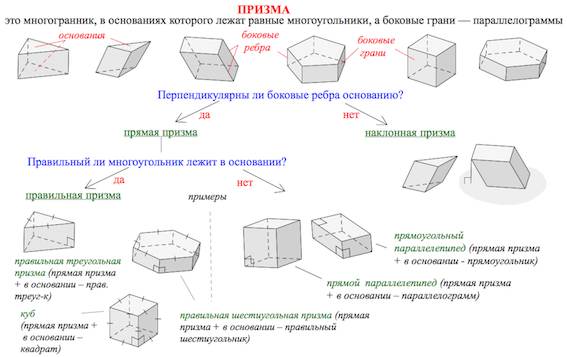
Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем подробный разговор.

Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и параллелограммов .

Боковые грани – все грани, кроме оснований ( являются параллелограммами ).

Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике.

Смотрите также «Объем призмы. Площадь поверхности призмы».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Источник

Правильная четырехугольная призма

Элементы правильной четырехугольной призмы

Свойства правильной четырехугольной призмы

Формулы для правильной четырехугольной призмы

Указания к решению задач

При решении задач на тему «правильная четырехугольная призма» подразумевается, что:

Правильная призма — призма в основании которой лежит правильный многоугольник, а боковые ребра перпендикулярны плоскостям основания. То есть правильная четырехугольная призма содержит в своем основании квадрат. (см. выше свойства правильной четырехугольной призмы)

Задача.

Диагональ правильной призмы образует с диагональю основания и высотой призмы прямоугольный треугольник. Соответственно, по теореме Пифагора диагональ заданной правильной четырехугольной призмы будет равна:
√( ( 12√2 ) 2 + 14 2 ) = 22 см

Задача

Определите полную поверхность правильной четырехугольной призмы, если ее диагональ равна 5 см, а диагональ боковой грани равна 4 см.

Решение.
Поскольку в основании правильной четырехугольной призмы лежит квадрат, то сторону основания (обозначим как a) найдем по теореме Пифагора:

a 2 + a 2 = 5 2
2a 2 = 25
a = √12,5

Высота боковой грани (обозначим как h) тогда будет равна:

h 2 + 12,5 = 4 2
h 2 + 12,5 = 16
h 2 = 3,5
h = √3,5

Площадь полной поверхности будет равна сумме площади боковой поверхности и удвоенной площади основания

Источник

Правильная четырехугольная призма

Четырехугольная призма — это многогранник, две грани которого являются равными квадратами, лежащими в параллельных плоскостях, а остальные грани (боковые грани) — параллелограммами, имеющими общие стороны с этими квадратами.

Основания призмы являются равными квадратами.

Боковые грани призмы являются прямоугольниками.

Боковые рёбра призмы параллельны и равны.

Размеры призмы можно выразить через длину стороны a и высоту h.

Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания.

Формула площади поверхности четырехугольной призмы:

Источник

Объём и площадь поверхности правильной четырёхугольной призмы

В школьной программе по курсу стереометрии изучение объёмных фигур обычно начинается с простого геометрического тела — многогранника призмы. Роль её оснований выполняют 2 равных многоугольника, лежащих в параллельных плоскостях. Частным случаем является правильная четырёхугольная призма. Её основами являются 2 одинаковых правильных четырёхугольника, к которым перпендикулярны боковые стороны, имеющие форму параллелограммов (или прямоугольников, если призма не наклонная).

Как выглядит призма

Правильной четырёхугольной призмой называется шестигранник, в основаниях которого находятся 2 квадрата, а боковые грани представлены прямоугольниками. Иное название для этой геометрической фигуры — прямой параллелепипед.

Рисунок, на котором изображена четырёхугольная призма, показан ниже.

На картинке также можно увидеть важнейшие элементы, из которых состоит геометрическое тело. К ним принято относить:

Иногда в задачах по геометрии можно встретить понятие сечения. Определение будет звучать так: сечение — это все точки объёмного тела, принадлежащие секущей плоскости. Сечение бывает перпендикулярным (пересекает рёбра фигуры под углом 90 градусов). Для прямоугольной призмы также рассматривается диагональное сечение (максимальное количество сечений, которых можно построить — 2), проходящее через 2 ребра и диагонали основания.

Если же сечение нарисовано так, что секущая плоскость не параллельна ни основам, ни боковым граням, в результате получается усечённая призма.

Для нахождения приведённых призматических элементов используются различные отношения и формулы. Часть из них известна из курса планиметрии (например, для нахождения площади основания призмы достаточно вспомнить формулу площади квадрата).

Площадь поверхности и объём

Чтобы определить объём призмы по формуле, необходимо знать площадь её основания и высоту:

Так как основанием правильной четырёхгранной призмы является квадрат со стороной a, можно записать формулу в более подробном виде:

Если речь идёт о кубе — правильной призме с равной длиной, шириной и высотой, объём вычисляется так:

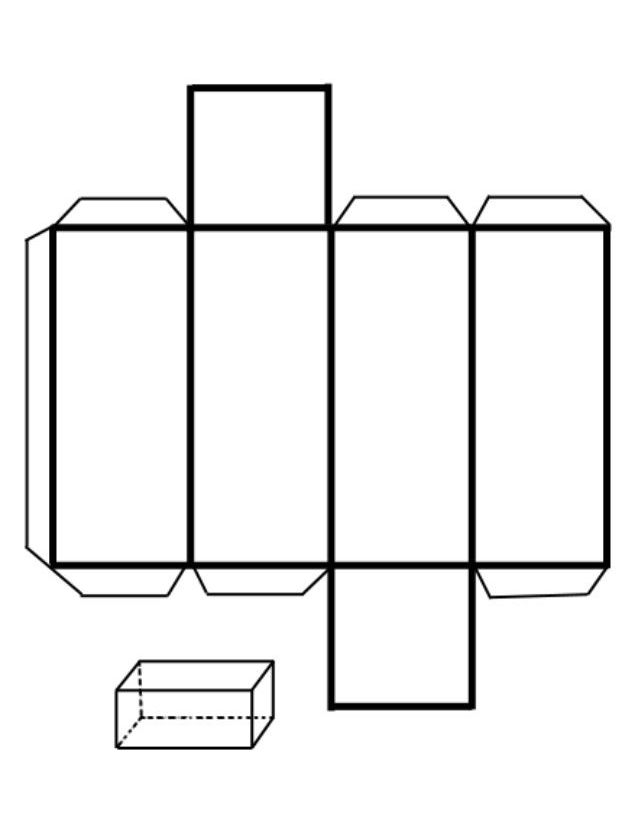
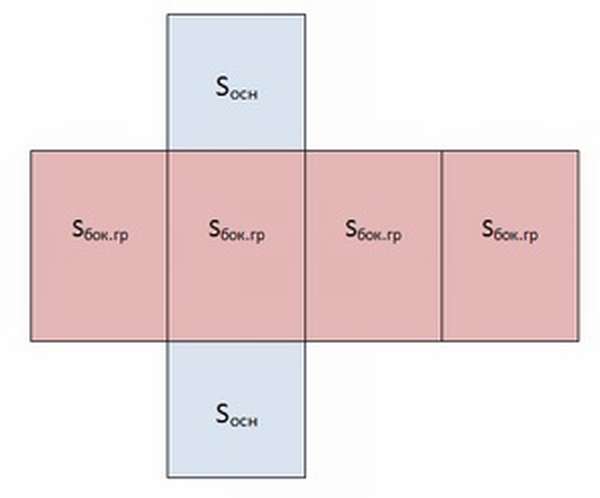
Чтобы понять, как найти площадь боковой поверхности призмы, необходимо представить себе её развёртку.

Из чертежа видно, что боковая поверхность составлена из 4 равных прямоугольников. Её площадь вычисляется как произведение периметра основания на высоту фигуры:

С учётом того, что периметр квадрата равен P = 4a, формула принимает вид:

Для вычисления площади полной поверхности призмы нужно к боковой площади прибавить 2 площади оснований:

Sполн = Sбок + 2Sосн

Применительно к четырёхугольной правильной призме формула имеет вид:

Для площади поверхности куба:

Зная объём или площадь поверхности, можно вычислить отдельные элементы геометрического тела.

Нахождение элементов призмы

Часто встречаются задачи, в которых дан объём или известна величина боковой площади поверхности, где необходимо определить длину стороны основания или высоту. В таких случаях формулы можно вывести:

Чтобы определить, какую площадь имеет диагональное сечение, необходимо знать длину диагонали и высоту фигуры. Для квадрата d = a√2. Из этого следует:

Для вычисления диагонали призмы используется формула:

Чтобы понять, как применять приведённые соотношения, можно попрактиковаться и решить несколько несложных заданий.

Примеры задач с решениями

Вот несколько заданий, встречающихся в государственных итоговых экзаменах по математике.

В коробку, имеющую форму правильной четырёхугольной призмы, насыпан песок. Высота его уровня составляет 10 см. Каким станет уровень песка, если переместить его в ёмкость такой же формы, но с длиной основания в 2 раза больше?

Следует рассуждать следующим образом. Количество песка в первой и второй ёмкости не изменялось, т. е. его объём в них совпадает. Можно обозначить длину основания за a. В таком случае для первой коробки объём вещества составит:

Для второй коробки длина основания составляет 2a, но неизвестна высота уровня песка:

Поскольку V₁ = V₂, можно приравнять выражения:

После сокращения обеих частей уравнения на a² получается:

В результате новый уровень песка составит h = 10 / 4 = 2,5 см.

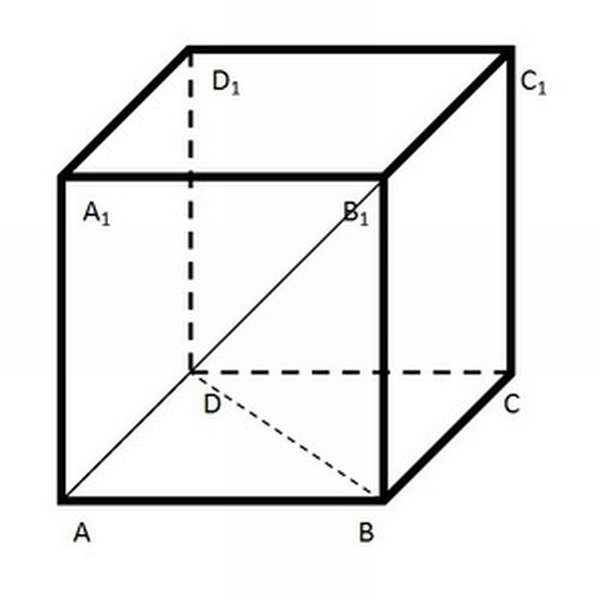
ABCDA₁B₁C₁D₁ правильная призма. Известно, что BD = AB₁ = 6√2. Найти площадь полной поверхности тела.

Чтобы было проще понять, какие именно элементы известны, можно изобразить фигуру.

Поскольку речь идёт о правильной призме, можно сделать вывод, что в основании находится квадрат с диагональю 6√2. Диагональ боковой грани имеет такую же величину, следовательно, боковая грань тоже имеет форму квадрата, равного основанию. Получается, что все три измерения — длина, ширина и высота — равны. Можно сделать вывод, что ABCDA₁B₁C₁D₁ является кубом.

Длина любого ребра определяется через известную диагональ:

Площадь полной поверхности находится по формуле для куба:

Sполн = 6a² = 6·6² = 216

В комнате производится ремонт. Известно, что её пол имеет форму квадрата с площадью 9 м². Высота помещения составляет 2,5 м. Какова наименьшая стоимость оклейки комнаты обоями, если 1 м² стоит 50 рублей?

Поскольку пол и потолок являются квадратами, т. е. правильными четырёхугольниками, и стены её перпендикулярны горизонтальным поверхностям, можно сделать вывод, что она является правильной призмой. Необходимо определить площадь её боковой поверхности.

Длина комнаты составляет a = √9 = 3 м.

Обоями будет оклеена площадь Sбок = 4·3·2,5 = 30 м².

Наименьшая стоимость обоев для этой комнаты составит 50·30 = 1500 рублей.

Таким образом, для решения задач на прямоугольную призму достаточно уметь вычислять площадь и периметр квадрата и прямоугольника, а также владеть формулами для нахождения объёма и площади поверхности.

Источник