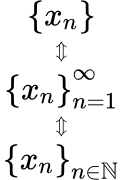Что значит последовательность сходится и последовательность расходится

Числовая последовательность

Определение 1. Числовой последовательностью называется функция, аргументом которой является множество всех натуральных чисел, или множество первых n натуральных чисел.

Обозначается числовая последовательность так:

где −i-ый член последовательности.

При словестном задании последовательности, описывается из каких элементов она состоит.

Последовательность нечетных чисел:

Последовательность простых чисел :

Последовательности (1) и (2) мы задали словестно.

Последовательность нечетных чисел аналитически задается формулой

Отметим, что последовательность простых чисел невозможно задать аналитически.

Пример задания рекуррентной последовательности:

В этой последовательности

Пример стационарной последовательности:

Возрастающие и убывающие последовательности

Определение 3. Последовательность, в которой каждый последующий член (кроме первого) больше предыдующего, называется возрастающей :

Определение 4. Последовательность, в которой каждый последующий член (кроме первого) меньше предыдующего, называется убывающей :

Пример 1. Выяснить, монотонна ли последовательность

Решение. Запишем n+1 член последовательности (подставим вместо n, n+1):

Найдем разность членов и :

.

(3)

Так как n=1,2,3. то правая часть уравнения (3) положительна. Тогда:

Таким образом, каждый последующий член последовательности больше предыдующего. Следовательно последовательность является возрастающим (и монотонным).

Пример 2. Выяснить, при каких значениях a последовательность (b_n) является возрастающей и при каких, убывающей:

Решение. Запишем n+1 член последовательности (вместо n подставим n+1):

Найдем разность членов и :

(4)

Посмотрим на правую часть выражения (4). Если a 10, то . Тогда последовательность является убывающей. При a=10 . Последовательность имеет одинаковые члены:

т.е. имеем дело с последовательностью

Очевидно, что последовательность (5) не является монотонной. Она является стационарной последовательностью.

Ограниченные и неограниченные последовательности

Определение 5. Последовательность (y_n) называется ограниченной сверху, если существует такое число k, что y_n Определение 6. Последовательность (y_n) называется ограниченной снизу, если существует такое число k, что y_n>k при любом n.

Определение 7. Последовательность (y_n) называется ограниченной, если она ограничена и сверху, и снизу.

Пример 3. Показать, что последовательность (a_n) является монотоннной и ограниченной:

Решение. Запишем n+1 член последовательности (вместо n подставим n+1):

Найдем разность членов и :

(6)

Правая часть равенства (6) положительна при любых натуральных чисел n. Следовательно последовательно (a_n) возрастающая (и монотонная).

Далее, сделаем эквивалентное преобразование для проследовательности (5):

Из выражения (7) видно, что при любых n a_n≤1. Т.е. хотя последовательность возрастает, то остается меньше числа 1 (ограничена сверху). Запишем несколько членов данной последовательности, задав n=1,2,3.

Так как последовательность возрастающая, то все члены последовательности не меньше . Тогда последовательность ограничена также и снизу. Таким образом последовательность ограничена и всерху, и снизу, т.е. является ограниченной последовательностью.

Сходящиеся и расходящиеся последовательности

Рассмотрим две числовые последовательности:

На координатной прямой изобразим члены этих последовательностей:

Предел числовой последовательности

Точка, к которой приближаются члены последовательности при увеличении n, называется пределом последовательности. Для последовательности (10) пределом является число 0. Более строго предел последовательности определяется так:

Определение 8. Число k называют пределом последовательности (y_n), если для любой заранее выбранной окресности точки k, можно выбрать такой номер n₀, чтобы все члены последовательности, начиная с номера n₀ содержались в указанной окрестности.

Если k является пределом последовательности (y_n), то пишут ( стремится к k или сходится к k).

Обозначают это так:

Выраженние (11) читается так: предел проследовательности , при стремлении n к бесконечности равен k.

Изложим некоторые пояснения к определению 8.

Пусть выполнено (11). Возьмем окрестность точки k, т.е. интервал , где радиус этой окрестности ( >0). По определению, существует номер n₀, начиная с которого вся последовательность содержится в указанной окресности, т.е.

.

Если же взять другую окресность (пусть ), то найдется другой номер n₁, начиная с которого, вся последовательность содержится в указанной окрестности, но этот номер будет больше n₁ > n₀.

Пример 4. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 0. Пусть ее радиус равен r. Тогда всегда можно выбирать n₀ так, чтобы .

Пусть, например, r=0.001. Вычислим n‘ из уравнения

.

В качестве n₀ берем 501. Имеем:

.

Запишем члены последовательности (12) начиная с номера 501:

.

Далее, учитывая (13), имеем:

.

Следовательно, все члены последовательности (12) начиная с номера 501 попадают в окресность . А по определению 8, это означает:

Пример 5. Дана полследовательность (y_n):

Доказать, что .

Решение. Найдем любую окрестность точки 2. Пусть ее радиус равен r. Тогда всегда можно выбирать n₀ так, чтобы

.

.

Неравенство в (17) всегда выполняется так как n₀ натуральное число, а правая часть неравенства отрицательно (это означает, что для любого n₀). Из неравенства (16) можно найти номер n₀, начиная с которого члены последовательности попадают в окресность (2−r; 2+r). Например, пусть r=0.001, тогда . Тогда нужно брать n₀=2000. И тогда все члены последовательности, начиная с номера 2000 попадают в окрестность (2−r; 2+r).

Запишем члены последовательности, начиная с номера 2000:

.

Легко проверить, что . Тогда, учитывая, что данная последовательность возрастающая (см. пример 1), получим:

.

Пример 6. Найти предел последовательности

Решение. Выполним некоторые преобразования выражения (18):

Тогда последовательность (18) можно переписать так:

(19)

Как видно из (19), пройдя по членам последовательности слева направо, из числа 1 вычитается все меньшее и меньшее положительное число. Т.е. последовательность приближается к числу 1. Тогда 1 является пределом последовательности (19) и (18):

Свойства сходящихся последовательностей

Сходящиеся последовательности обладают рядом свойств.

Свойство 1. Если последовательность сходится, то только к одному пределу.

Свойство 2. Если последовательность сходится, то она ограничена.

Свойство 3. Если последовательность монотонна и ограничена, то она сходится (теорема Вейерштрасса).

Предел стационарной последовательности равен значению любого члена последовательности:.

Теорема. Если , то

1. Предел суммы равен сумме пределов:

2. Предел произведения равен произведению пределов:

3. Предел частного равен частному пределов:

4. Постоянный множитель можно вывести за знак предела:

Пример 7. Найти предел последовательности:

Решение. Так как , то

.

Пример 8. Найти предел последовательности:

Решение. Применив правило «предел суммы» теоремы, получим

.

Пример 9. Вычислить:

Решение. Делим числитель и знаменатель дроби на наивысшую из имеющихся степень переменного n. Далее используем правило «предел суммы» для числителя и знаменателя и правило «предел частного»:

Источник

Определение числовой последовательности

Определение

Далее мы будем считать, что элементами последовательности являются действительные числа.

Другими словами числовая последовательность – это функция, областью определения которой является множество натуральных чисел. Число элементов последовательности бесконечно. Среди элементов могут встречаться и члены, имеющие одинаковые значения. Также последовательность можно рассматривать как нумерованное множество чисел, состоящее из бесконечного числа членов.

Примеры последовательностей

Примеры неограниченно возрастающих последовательностей

Примеры последовательностей, сходящихся к конечному числу

Примеры расходящихся последовательностей

Последовательность с членами, распределенными в интервале (0;1)

Теперь рассмотрим более интересную последовательность. На числовой прямой возьмем отрезок [0;1]. Поделим его пополам. Получим два отрезка. Пусть
.
Каждый из отрезков снова поделим пополам. Получим четыре отрезка. Пусть
.
Каждый отрезок снова поделим пополам. Возьмем

.
И так далее.

Поскольку существуют подпоследовательности, сходящиеся к различным значениям, то сама исходная последовательность не сходится ни к какому числу.

Последовательность, содержащая все рациональные числа

Теперь построим последовательность, которая содержит все рациональные числа. Причем каждое рациональное число будет входить в такую последовательность бесконечное число раз.

Рациональное число r можно представить в следующем виде:
,
где – целое; – натуральное.
Нам нужно каждому натуральному числу n поставить в соответствие пару чисел p и q так, чтобы любая пара p и q входила в нашу последовательность.

Способ нумерации рациональных чисел

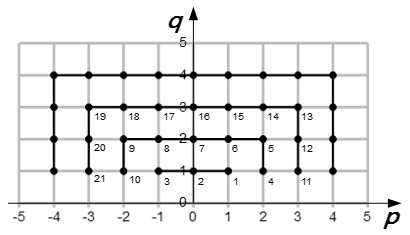
Итак, для верхней стороны первого квадрата имеем:
.
Далее нумеруем верхнюю часть следующего квадрата:

.
Нумеруем верхнюю часть следующего квадрата:

.
И так далее.

Тогда из построенной нами последовательности, мы можем выделить подпоследовательность (имеющую бесконечное число элементов), все элементы которой равны наперед заданному рациональному числу. Поскольку построенная нами последовательность имеет подпоследовательности, сходящиеся к различным числам, то последовательность не сходится ни к какому числу.

Заключение

Здесь мы дали точное определение числовой последовательности. Также мы затронули вопрос о ее сходимости, основываясь на интуитивных представлениях. Точное определение сходимости рассматривается на странице Определение предела последовательности. Связанные с этим свойства и теоремы изложены на странице Предел последовательности – основные теоремы и свойства.

Источник

11. Сходящиеся и расходящиеся последовательности. Предел последовательности

Последовательность <а_n> называется сходящейся, если существует такое вещественное число А, что последовательность <а_n – А> является бесконечно малой. Число А будет пределом последовательности: .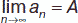

Бесконечно малые последовательности являются сходящимися с пределом, равным нулю, бесконечно большие – расходящимися (сходящимися к бесконечности).

Точка бесконечной прямой называется предельной точкой последовательности, если в любой ее ?–окрестности содержится бесконечно много элементов данной последовательности.

Лемма. Каждая сходящаяся последовательность имеет только одну предельную точку, совпадающую с ее пределом.

Основные свойства сходящихся последовательностей:

1) всякая сходящаяся последовательность имеет один предел;

2) сходящаяся последовательность <a_n> ограниченна;

Следствия:

1) если все члены сходящейся последовательности <a_n> не отрицательны (не положительны), то предел последовательности есть число неотрицательное (неположительное), ;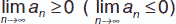

2) если все элементы сходящейся последовательности <a_n> находятся на отрезке [a, b], то и предел этой последовательности <a_n> лежит на данном отрезке, ;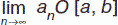

Теорема о сходимости монотонной ограниченной последовательности. Всякая неубывающая (невозрастающая) последовательность <a_n>, ограниченная сверху (снизу) сходится. Иначе для того чтобы монотонная последовательность сходилась необходимо и достаточно, чтобы она была ограниченна.

Данный текст является ознакомительным фрагментом.

Источник