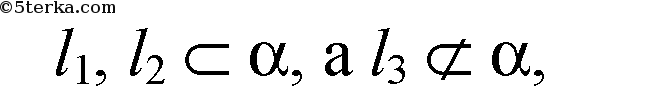Что значит попарное пересечение прямых

Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые?

Сразу говорю, что задачу решать НЕ НАДО. Оставьте это мне. Я просто хочу разобраться, что означает «попарное пересекающиеся прямые».

У меня есть такая интерпретация: Имеется в виду, что все прямые «собраны» в пары. И каждая такая «сладкая парочка» пересекается другой такой же парой или «одиночной» прямой. Правда в этом конкретном случае «одиночек» нет, ибо количество прямых четное.

Я правильно все понимаю, или моя интерпретация неверна? Если неверна, то что тогда имеется в виду?

задан 23 Май ’13 13:26

I_Robot
183 ● 4 ● 17 ● 38
92&#037 принятых

Здесь имеется в виду, что какие бы две прямые из четырёх мы ни взяли, они будут пересекаться.

«они будут пересекаться.» Может быть, более точным будет сказать «они ДОЛЖНЫ пересекаться»?

Кстати, преобразуйте пожалуйста свой комментарий в ответ, дабы я мог закрыть вопрос.

3 ответа

Можно сказать «они пересекаются», «они должны пересекаться», «они будут пересекаться». Это всё одна и та же мысль. Суть в том, что любые две прямые из четырёх имеют точку пересечения. Фактически, это означает, что среди прямых нет параллельных (хотя в принципе такие прямые могли бы быть в какой-то другой ситуации, и тогда ответ был бы другим). Слово «попарно» вообще очень часто используется в математике. Например, «даны три попарно различных числа». Это значит, что первое число не равно второму, а также не равно третьему, а второе число не равно третьему.

отвечен 23 Май ’13 13:57

Если речь идет об одной паре прямых, то в одной точке, а ежели о двух парах и более, то рассматриваютя разные варианты расположения уже самих пересекающихся пар прямых.

отвечен 13 Сен ’15 13:02

Можете ли дать ссылку на определение «попарно пересекающиеся прямые» из учебника? Например как построить 5 попарно пересекающихся прямых? Можно-ли из этого сделать вывод, что одна прямая может пересекать лишь 2 других?

отвечен 22 Сен ’17 19:18

Здравствуйте

Источник

Пересечение прямых, угол и координаты пересечения

IP76 > Пересечение прямых, угол и координаты пересечения

Не такая тривиальная задача, скажу я вам. Всякий раз, когда возникает необходимость посчитать координату пересечения пары прямых, каждая из которых задана парой точек, снова беру блокнот и вывожу пару формул. И всякий раз – блин, ну это уже когда-то было, опять надо что-то делать с параллельными прямыми, опять появляется пакостная строго вертикальна линия, когда на (x₁-x₂) никак не разделить и т.д.

Поэтому – в подборку теории и практики, пригодится, сэкономим блокнот, спасем дерево.

Коэффициенты А, B, C

Все помним со школы формулу:

Тоже самое, но с претензией на образование (некоторые индивидуумы утверждают, что существует такая, и только такая, и никакая другая, формулировка):

Те же фаберже, только сбоку.

В теории надо составить и решить систему уравнений для первой и второй линии, где переменными будут X и Y точки пересечения.

Загвоздка в том, что мы не знаем коэффициенты для обеих линий.

В нашем случае известны координаты двух точек, по которым проходит линия. Поэтому мне, как последователю геометрического агностицизма, более привлекательная следующая формула:

Путем несложных операций приходим к следующей записи:

Глядя на вариант в исполнении высшего образования, получаем следующие формулы для нахождения коэффициентов:

Пока все идет отлично, нигде вероятного деления на ноль не встретилось.

Итак, мы можем легко найти два набора коэффициентов для первой и второй прямых. Переходим к системе уравнений.

Система уравнений

Как правило, подобная система уравнений решается путем выражения одной переменной через другую, подстановкой во второе уравнение, получая таким образом уравнение одной переменной. Далее переменная находится, подставляется, решается. Или определяется, что система решения не имеет.

Но нас интересует метод Крамера. Потому что с помощью этого метода можно получить сразу значения для обеих переменных, без дополнительных телодвижений.

Сразу же запишем метод под нашу систему.

Имеем следующую систему:

Исходя из метода, решение выглядит так:

Ага! Вот и возможное деление на ноль, скажете вы. И правильно! В этой, в высшей степени непозволительной ситуации, когда знаменатель равен нулю, решения нет, прямые либо параллельны, либо совпадают (что, впрочем, частный случай параллельности). В коде, естественно, этот момент надо учитывать.

Практика 1

Частные случаи

Принадлежность точки отрезку

В общем случае, чтобы определить принадлежность точки отрезку, надо установить две вещи:

Займемся пунктом 2. Данный факт можно установить двумя способами:

Практика показывает, что арифметический способ быстрее примерно в 3 раза. Когда-то я считал, что операции сравнения самые быстрые. Это давно уже не так.

Угол пересечения прямых

Угол пересечения прямых — это угол пересечения направляющих векторов. Т.е., взяв уже знакомые ранее точки p₁ и p₂, получим направляющий вектор V(p₁,p₂), и аналогично второй вектор M(p₃,p₄). В теории мы должны вычислить достаточно «затратную» функцию, с корнями, квадратами, дробями и арккосинусом.

Давайте не будем останавливаться на ней, она долгая, нудная и в нашем случае ненужная. Рассмотрим вектор:

Рис.4. Вектор V(p₁,p₂)

α — угол наклона вектора к оси X, который можно найти, как:

Что-то знакомое? Да это ни что иное, как коэффициенты в уравнении прямой от образованных фанатов. Может они и правы в своем испепеляющем фанатизме…

Одним словом, коэффициенты (расстояния) у нас уже есть по обеим прямым.

Рис.5. Пересекающиеся вектор V(p₁,p₂) и вектор M(p₃,p₄)

Судя по рисунку, угол между векторами, это сумма углов наклона векторов к оси X. Ммм… не совсем так, на самом деле это разность.

Рис.6. Пересекающиеся векторы в положительной Y

По рисунку явно видно, что угол между векторам это γ = (β — α).

В предыдущем примере все правильно, просто знаки углов разные, т.к. находятся по разные стороны от оси X, а формула работает та же.

От теории к практике

Теперь в плане практического применения. Мне нужно точно знать, откуда, куда и в каком направлении этот угол. В теории, углом между прямыми считается наименьший из пары γ и (180-γ). Так вот, нам это не надо. Какой угол получится – такой нам и нужен.

Поэтому, под углом между векторами понимаем угол от вектора V(p1,p2) к вектору M(p3,p4). Если знак угла – отрицательный, понимаем, что он против часовой стрелки, иначе – по часовой стрелке.

Следует заметить, что, зная коэффициенты, для нахождения угла пересечения, координаты уже не нужны. Листинг таков:

Источник

Про смартфон — цены, обзоры и реальные отзывы покупателей

На сайте Pro-Smartfon найдёте отзывы и обзоры топовых смартфонов 2017 года. Всё о плюсах и минусах мобильных телефонов. Свежие фотографии, цены и реальные отзывы покупателей о лучших смартфонах

Что значит попарно пересекаются

Решебник по геометрии за 10 класс (Л.С.Атанасян, 2001 год),
задача №15
к главе «Введение».

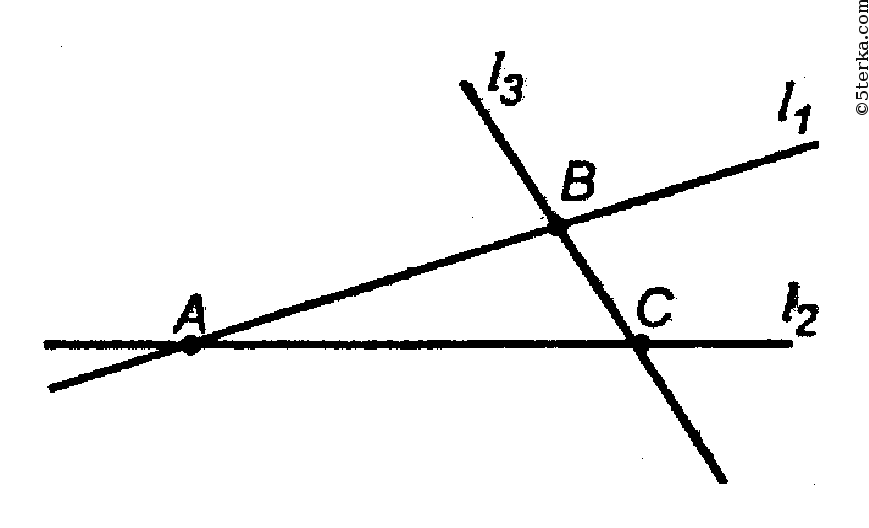
Каждая из трех точек принадлежит одновременно прямым.

Через три точки по аксиоме А₁ можно провести единственную плоскость α. Поэтому отрезки АВ,

ВС и АС лежат в плоскость α

(по аксиоме А₂), значит, прямые, которым принадлежат эти отрезки, тоже лежат в α.

Рассмотрим второй случай:

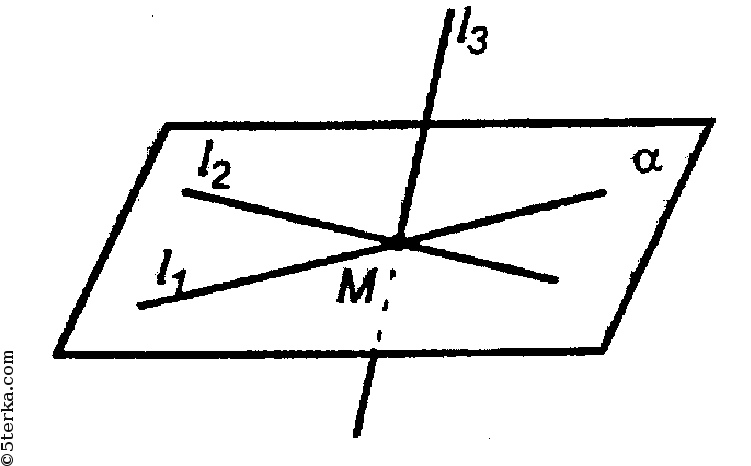
но и пересекается с l₂ и l₁ в точке М.

То есть прямые имеют общую точку, но не лежат в одной плоскости.

ПОПА́РНО, нареч. По двое, парами. Лебеди прилетают почти всегда попарно. С. Аксаков, Записки ружейного охотника. [Солдаты] стояли попарно, в полной караульной форме. Катаев, Белеет парус одинокий.

Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека

ПОПА’РНО, нареч. По-двое, парами. Ученики шли п.

Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека

попарно

Делаем Карту слов лучше вместе

Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.

Насколько понятно значение слова сонливый (прилагательное):

Синонимы к слову «попарно»

Предложения со словом «попарно»

Цитаты из русской классики со словом «попарно»

Понятия, связанные со словом «попарно»

Отправить комментарий

Дополнительно

Предложения со словом «попарно»:

Мы проследим эту фазу до следующей ступени развития, когда, под влиянием крепостного права, община примет ещё новую форму: это уже будет самоуправление каторги, коллективизм цепи, сковывающий людей попарно.

После этого стойки попарно перекрещивают между собой, а чтобы удержать их в таком состоянии, скрепляют места пересечения скрепкой.

Тотчас за телом шли двенадцать пар лилипутов, держась попарно за руки, одетые в чёрные кафтаны, с длинными, волочившимися по земле мантиями, обшитыми флёром.

Можете ли дать ссылку на определение «попарно пересекающиеся прямые» из учебника? Например как построить 5 попарно пересекающихся прямых, сколько точек пересечения у них может быть? Можно-ли из этого сделать вывод, что одна прямая может пересекать лишь 2 других?

задан 22 Сен ’17 19:30

2 ответа

Каждая из 5-ти прямых должна пересечь остальные 4 прямые. Нужную конфигурацию образуют, например, продолжения сторон правильного 5-угольника.

отвечен 22 Сен ’17 19:35

@Анатолий75: это чисто языковой оборот. Имеется в виду, что любая пара прямых пересекается (то есть среди них нет параллельных). Вопрос о том, сколько точек пересечения при этом может образоваться, требует разбора случаев.

Если все 5 прямых проходят через одну точку, то точка пересечения одна. Если нет тройных и более точек пересечения, то ответом будет 5*4/2=10 точек пересечения. Если 4 прямые проходят через одну точку, а пятая их отдельно пересекает, то точек получается 5. Если есть ровно одна тройная точка пересечения, то всего точек получится 8. Наконец, могут быть две тройные точки пересечения, и тогда точек 6.

Итого имеем 1, 5, 6, 8 или 10 точек пересечения.

Источник

Пересекающиеся прямые

Пересекающиеся прямые — это в евклидовой геометрии пересечение двух прямых может быть пустым множеством, точкой или прямой. Различение этих случаев и поиск точки пересечения используется, например, в компьютерной графике, при планировании движения и для обнаружения столкновений.

Содержание:

Понятие пересекающихся прямых

Определение. Если две прямые имеют только одну общую точку, то такие прямые называют пересекающимися.

На рисунке 2.291 прямые пересекаются в точке О.

Можно доказать такую теорему.

Теорема 1. Через две пересекающиеся прямые можно провести плоскость, и только одну.

Несколько прямых могут пересекаться не в одной точке, а, например, попарно. На рисунке 2.292 изображено пересечение трех прямых, каждые две из которых пересекаются только в одной точке. При этом образуется треугольник и вся эта фигура всегда лежит в одной плоскости.

Четыре прямые, каждые две из которых имеют только одну общую точку, образуют четырехугольник (рис. 2.293).

На рисунках 2.294, 2.295 изображены куб и тетраэдр, у которых продолжены их ребра. Мы видим, что в каждой вершине куба и тетраэдра пересекаются три прямые.

Эта лекция взята со страницы полного курса лекций по изучению предмета «Математика»:

Смотрите также дополнительные лекции по предмету «Математика»:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник

Пересечение прямых. Точка пересечения двух прямых

Если точка M, является точкой пересечения двух прямых, то она должна принадлежать этим прямым, а ее координаты удовлетворять уравнения этих прямых.

Точка пересечения двух прямых на плоскости

Если система уравнений:

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Вычтем из первого уравнения второе

Из первого уравнения найдем значение x

Подставим значение x во второе уравнение и найдем значение y

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

В первое уравнение подставим значения x и y из второго и третьего уравнений.

Подставим значение t во второе и третье уравнение

Решение: Для вычисления координат точки пересечения прямых, решим систему уравнений:

Из второго уравнения выразим y через x

Подставим y в первое уравнение

Решение: Обе прямые заданы уравнениями с угловым коэффициентом. Так как k ₁ = k ₂ = 2, то прямые параллельны. Так как эти прямые не совпадают то точек пересечения нет.

Решим также эту задачу используя систему уравнений:

Вычтем из первого уравнения второе

Ответ. Прямые не пересекаются (прямые параллельны).

Решение: Подставим координаты точки N в уравнения прямых.

Точка пересечения двух прямых в пространстве

Если система уравнений:

Решение: Составим систему уравнений

К шестому уравнению добавим пятое уравнение

Подставим значение b в четвертое и пятое уравнения

x = a + 1 y = a + 1 z = a + 1 a = 0 a = 0 b = 1 => x = 0 + 1 = 1 y = 0 + 1 = 1 z = 0 + 1 = 1 a = 0 a = 0 b = 1

Ответ. Прямые пересекаются в точке с координатами (1, 1, 1).

Решение: Составим систему уравнений заменив во втором уравнении параметр t на a

Подставим значение t из шестого уравнения в остальные уравнения

Источник