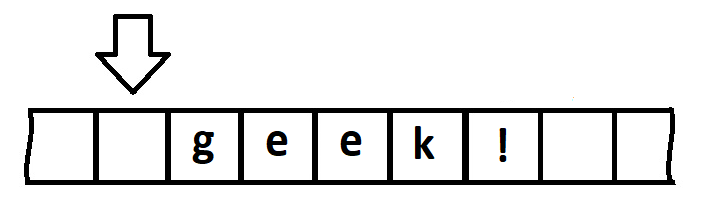Что значит полный по тьюрингу
Наследие Тьюринга: машина, тест и полнота
Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
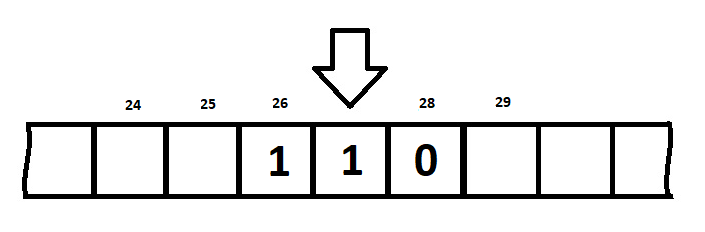
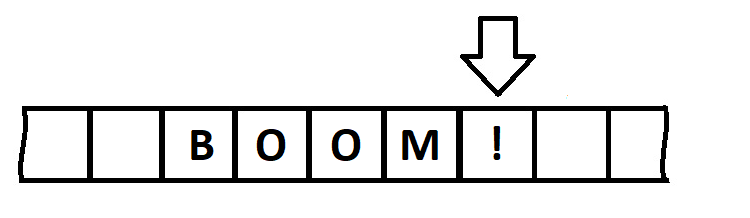
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полный\не полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
Если вы не учились профессии программиста в вузе или не ходили в специальную школу, то, возможно «Машина Тьюринга» для вас просто дешифратор из курса истории или фильма «Игра в имитацию». В действительности всё немного сложнее, любому уважающему себя программисту необходимо знать и понимать, что это такое.
Что такое машина Тьюринга
Для того, чтобы представить простейшую машину Тьюринга, взглянем на её художественную реализацию:
Это бесконечная лента, не имеющая ни начала, ни конца, поделённая на ячейки. Для работы с ней мы используем некое управляющее устройство (автомат), для визуализации выбрана каретка. В каждый момент времени она имеет состояние qj и считывает содержимое ячейки ai. О том, что происходит в остальной части ленты, каретка не знает, соответственно оперировать она может только текущими данными. Всего возможно три типа действий, зависящий от этой композиции:
Что-то похожее реализовано в электронных таблицах: там тоже условно неограниченное поле, вы можете изменить значение ячейки, изменить действие или перейти на другую ячейку.
Создадим таблицу для реализации алгоритма Тьюринга:
Символами _Л, _П, _Н обозначим направление движения автомата – соответственно сдвиг «влево», «вправо» или неподвижное положение.
Пусть наша лента выглядит так:
Начальное положение – крайняя правая ячейка, остановка – в пустой клетке. Догадались как она будет выглядеть после завершения алгоритма?
На указанном примере всё выглядит довольно просто. Можете поиграть с увеличением алфавита, преобразованием состояний, помещением начальной позиции не в крайнюю позиции, условиями выхода из цикла и т.д. Фактически, практически любую задачу преобразования можно решить с помощью машины Тьюринга.
Зачем это программисту
Машина Тьюринга позволяет размять мозги и взглянуть на решение задачи иначе. В конечном счёте, с той же целью следует познакомиться с:
Но машина Тьюринга – базовая теория алгоритмов, которая помогает думать не столько о средствах языка, сколько о различных путях решения задачи. Для профессионального роста – это необходимый навык.
Полнота по Тьюрингу
Ещё один важный вопрос, связанный с именем известного математика. На форумах и в статьях вы неоднократно могли видеть выражение «полный\не полный язык программирования по Тьюрингу». Ответ на вопрос «что это означает?» возвращает нас к описанной выше теории. Как уже было сказано, машина Тьюринга позволяет выполнить любое преобразование, соответственно, вы можете реализовать на ней абсолютно любой алгоритм или функцию. То же самое относится и к языкам. Если с его помощью вы можете реализовать любой заданный алгоритм – он тьюринг-полный. Если в дело вступают ограничения синтаксиса или любые физические – не полный.
Тест по Тьюрингу
Последний раздел никак не связан с машиной. Тест Тьюринга – игра, в ходе которой человек с помощью текстовых сообщений взаимодействует одновременно с машиной и другим человеком, не видя их. Задача машины – ввести участника в заблуждение.
Такой тест на долгие годы предопределил развитие ИИ – программы вроде Элизы или PARRY строились именно на копировании человеческого поведения машиной. Уже позднее, когда стало понятно, что путь тупиковый, вектор развития был сдвинут в сторону изучения механизмов интеллекта. Однако до сих пор тема «способна ли мыслить машина» лежит в основе многих тестов, романов и кинофильмов.
Алан Тьюринг остался в истории не только человеком, совершившим важное открытие во время Второй мировой войны, но и подаривший миру несколько фундаментальных теорий, которыми пользуется человечество до сих пор.
Неожиданная полнота по Тьюрингу повсюду
Каталог программных конструкций, языков и API, которые неожиданно являются полными по Тьюрингу; последствия этого для безопасности и надёжности. Приложение: сколько компьютеров в вашем компьютере?
Любая достаточно сложная программа на Си или Фортране содержит заново написанную, неспецифицированную, глючную и медленную реализацию половины языка Common Lisp. — Десятое правило Гринспена
Полнота по Тьюрингу (Turing-completeness, TC) — это свойство системы при некотором простом представлении ввода и вывода реализовать любую вычислимую функцию.
Тьюринг-полнота — фундаментальное понятие в информатике. Она помогает ответить на многие ключевые вопросы, например, почему невозможно создание идеальной антивирусной программы. Но в то же время она является поразительно распространённым явлением. Казалось бы, компьютерной системе трудно достичь такой универсальности, чтобы выполнять любую программу, но получается наоборот: трудно написать полезную систему, которая немедленно не обратится в полную по Тьюрингу. Оказывается, что даже небольшой контроль над входными данными и преобразованием их в результат, как правило, позволяет создать тьюринг-полную систему. Это может быть забавным, полезным (хотя обычно нет), вредным или чрезвычайно небезопасным и настоящим подарком для хакера (см. о «теоретико-языковой безопасности», которая изучает методы взлома «странных машин» 1 ). Удивительные примеры такого поведения напоминают нам о том, что полнота по Тьюрингу таится повсюду, а защитить систему чрезвычайно сложно.
«Слишком мощные» языки программирования тоже могут спровоцировать неприятные DoS-атаки. Фаззер afl нашёл в OpenBSD такой roff, что способен на генерацию бесконечного цикла, злоупотребляя некоторыми правилами подстановки строк.
Многие конфигурации, специальные языки, инструменты или сложные игры, как выясняется, нарушают правило наименьшей власти и «случайно становятся полными по Тьюрингу», как шаблоны MediaWiki, sed или многократное повторение команд regexp/find-replace в редакторе. Вообще, любая форма замены строк или шаблонирования, или компиляции на лету с высокой вероятностью является тьюринг-полной системой сама или при повторении, так как они часто поддерживают лямбда-исчисление или переписывание термов языка или метки, например, эзотерические языки «///» или Thue.
С другой стороны, направление исследований компьютерной безопасности под названием «странные машины» (weird machines) часто выявляет поистине поразительные тьюринг-полные системы. Причём у разных людей они вызывают удивление в разной степени: одним кажется необычным то, что других не удивляет.
См. также
Ссылки
Приложение
Сколько компьютеров в вашем компьютере?
Некоторые увязают в спорах о странных машинах или о том, насколько «большим» станет агент ИИ: будет создан один такой, два, десять или миллионы. Неважно, поскольку это просто организационный вопрос. На самом деле важны входы и выходы системы: насколько работоспособна система в целом и какие ресурсы потребляет? Никого не волнует, если Google работает на 50 суперкомпьютерах, 50 000 мейнфреймах, 5 миллионах серверов, 50 млн встроенных/мобильных процессоров или на сочетании всего перечисленного. Неважно, что Google использует разнообразные чипы: от самодельных «тензорных процессоров» до уникальных кремниевых процессоров (Intel реализует их на чипах на процессоры Xeon для ряда крупнейших клиентов), FPGA, GPU, CPU до ещё более экзотического оборудования вроде квантовых компьютеров D-Wave. Важно только, чтобы она сохраняла конкурентоспособность и могла предоставлять услуги за умеренную плату. В конце концов, сегодня суперкомпьютер выглядит обычно как большое количество серверов в стойках с огромным количеством GPU и необычно высокоскоростными соединениями InfiniBand. То есть суперкомпьютер не так уж сильно отличается от дата-центра, как можно подумать. Любое из перечисленного оборудования может поддерживать многочисленные странные машины в зависимости от своей внутренней динамики и связности.
Аналогично, любую систему ИИ можно реализовать в виде одной гигантской нейронной сети или множества отдельных нейросетей, работающих асинхронно, или как гетерогенный набор микросервисов, или как «общество разума» и так далее. Всё это не особенно важно. С точки зрения сложности или рисков, не так важно, как именно организована система, пока она работает. Систему можно увидеть на многих уровнях, каждый из которых одинаково недействителен сам по себе, но полезен для разных целей в общей системе.
Вот пример плохо определённого вопроса: сколько компьютеров сейчас у вас в карманах и на столе? Сколько компьютеров в вашем «компьютере»? Думаете, только один? Давайте посмотрим внимательнее.
Речь идёт не только о CPU: в наше время транзисторы и процессорные ядра настолько дёшевы, что теперь часто имеет смысл выделять отдельные ядра на задачи реального времени, для повышения производительности, для безопасности, чтобы избежать нагрузки на основную ОС, для совместимости со старой архитектурой или существующего программным пакетом. Просто потому что DSP или ядро быстрее запрограммировать, чем создать специализированный ASIC, или потому что это самое простое из возможных решений. Кроме того, многие из этих компонентов могут использоваться в качестве вычислительных элементов, даже если они не предназначены или вообще скрывают эту функциональность.
«Удивительно, как много разнородных ядер процессора интегрированы в Intel Silvermont Moorefield SoC (ANN): x86, ARC, LMT, 8051, Audio DSP, каждый на своей прошивке и с поддержкой интерфейса JTAG
Здесь нет ничего необычного в историческом контексте, ведь даже самые первые мейнфреймы обычно включали в себя несколько компьютеров, где основной компьютер выполняет пакетную обработку, о вспомогательные компьютеры обеспечивают высокоскоростные операции ввода/вывода, которые в противном случае помешают основной машине своими прерываниями.
На практике же, кроме сообщества информационой безопасности (поскольку все эти компьютеры небезопасны и, следовательно, полезны для АНБ и вирусописателей), всем остальным пользователям всё равно, что под капотом наших компьютеров скрываются безумно сложные системы, которые более точно рассматривать как пёстрый зверинец из сотен компьютеров, неловко связанных друг с другом (непонятно, «сеть — это компьютер» или «компьютер — это сеть». ). Пользователь воспринимает и использует это как один компьютер.
1. Активная область исследований — создание языков и систем, которые тщательно спроектированы и гарантированно не являются тьюринг-полными (например. тотально функциональное программирование). Зачем прилагать столько усилий для создания языка, на котором невозможно написать многие программы? Дело в том, что полнота по Тьюрингу тесно связана с теоремой Гёделя о неполноте и теоремой Райса. Поэтому если разрешить TC, то мы теряем всевозможные свойства доказуемости. Наоборот, в не полном по Тьюрингу языке легко доказываются разные полезные вещи: например, что программа завершена, типобезопасная она или нет, что её легко преобразовать в логическую теорему, что она потребляет ограниченное количество ресурсов, что реализация протокола верна или эквивалентна другой реализации. Легко доказывается отсутствие побочных эффектов и что программу можно преобразовать в логически эквивалентный, но более быстрый вариант (это особенно важно для декларативных языков вроде SQL, где способность оптимизатора преобразовать запросы — ключ к приемлемой производительности. Хотя, конечно, на SQL можно делать удивительные вещи, такие как градиентный спуск для моделей машинного обучения, а некоторые расширения SQL делают его тьюринг-полным в любом случае, позволяя либо закодировать циклическую систему тегов, либо model DSL, либо вызвать PL/SQL и т.д.
Вот некоторая литература о странных машинах:
2. Хотя линейные нейросети эксплуатируют режим плавающей точкой с округлением до нуля для кодирования потенциально тьюринг-полного поведения (для RNN), но это незаметно в нормальной работе, что одновременно является случайным тьюринг-полным поведением и наглядным примером безопасного языка. ↑
3. Dwarf Fortress даёт часовые механизмы, поэтому полнота по Тьюрингу неудивительна. Но и вода реализована как простой клеточный автомат, поэтому есть даже больше способов получить тьюринг-полноту! Сейчас игровая вики называет четыре потенциальных способа создания логических вентилей: жидкости, механизмы часового механизма, минные тележки и логические вентили существ/животных с участием дверей и датчиков давления. ↑
4. Полная спецификация PDF исключительно раздута. Например, в простой программе просмотра PDF с поддержкой достаточного количества спецификации PDF, как браузер Google Chrome, можно играть в Breakout (потому что PDF включает собственное странное подмножество JavaScript). Официальная программа просмотра Adobe PDF поддерживает функциональность вплоть до трёхмерного САПР. ↑
Чтобы показать, что что-то является полным по Тьюрингу, достаточно показать, что это может быть использовано для моделирования некоторой полной системы по Тьюрингу. Например, императивный язык является полным по Тьюрингу, если у него есть условное ветвление (например, операторы «if» и «goto» или инструкция « переход при нулевом значении»; см. Компьютер с одним набором инструкций ) и возможность изменять произвольные объем памяти (например, возможность поддерживать произвольное количество элементов данных). Конечно, никакая физическая система не может иметь бесконечную память; но если игнорировать ограничение конечной памяти, большинство языков программирования в остальном являются полными по Тьюрингу.
СОДЕРЖАНИЕ
Нематематическое использование
В разговорной речи термины «полный по Тьюрингу» и «эквивалент по Тьюрингу» используются для обозначения того, что любой реальный компьютер общего назначения или компьютерный язык может приблизительно имитировать вычислительные аспекты любого другого реального компьютера общего назначения или компьютерный язык.
Формальные определения
В теории вычислимости для описания вычислительной мощности вычислительной системы (например, абстрактной машины или языка программирования ) используются несколько тесно связанных терминов :
История
Теория вычислимости
Теория вычислимости использует модели вычислений для анализа проблем и определения их вычислимости и при каких обстоятельствах. Первый результат теории вычислимости состоит в том, что существуют задачи, для которых невозможно предсказать, что (полная по Тьюрингу) система будет делать в течение сколь угодно длительного времени.
Эта невозможность создает проблемы при анализе реальных компьютерных программ. Например, невозможно написать инструмент, который полностью защищает программистов от написания бесконечных циклов или защищает пользователей от ввода данных, которые могут вызвать бесконечные циклы.
Вместо этого можно ограничить выполнение программы только в течение фиксированного периода времени ( тайм-аут ) или ограничить мощность инструкций управления потоком (например, предоставив только циклы, которые повторяются по элементам существующего массива). Однако другая теорема показывает, что существуют проблемы, решаемые с помощью полных по Тьюрингу языков, которые не могут быть решены никаким языком с ограниченными возможностями цикла (т. Е. Любым языком, гарантирующим, что каждая программа в конечном итоге остановится). Таким образом, любой такой язык не является полным по Тьюрингу. Например, язык, на котором программы гарантированно завершаются и останавливаются, не может вычислить вычислимую функцию, созданную диагональным аргументом Кантора для всех вычислимых функций на этом языке.
Оракулы Тьюринга
Цифровая физика
Все известные законы физики имеют последствия, которые можно вычислить с помощью серии приближений на цифровом компьютере. Гипотеза, называемая цифровой физикой, утверждает, что это не случайно, потому что сама Вселенная вычислима на универсальной машине Тьюринга. Это означало бы, что физически невозможно построить компьютер более мощный, чем универсальная машина Тьюринга.
Примеры
Большинство языков программирования (их абстрактные модели, возможно, с некоторыми конкретными конструкциями, предполагающими исключение конечной памяти), традиционные и нетрадиционные, являются полными по Тьюрингу. Это включает:
Некоторые системы перезаписи являются полными по Тьюрингу.
Непреднамеренная полнота по Тьюрингу
Некоторые игры и другое программное обеспечение являются полными по Тьюрингу случайно, то есть не намеренно.
Тьюринг-полнота Generic типов Java
Периодически на хабре можно встретить статьи о том, какие невероятные вещи можно сделать на шаблонах C++: конечные автоматы, лямбда-исчисление, машина Тьюринга и многое другое.
Параметризованные типы в Java традиционно считаются лишь пародией на шаблоны C++ (несмотря на то, что их даже сравнивать как-то некорректно), и причины этого несложно понять. Тем не менее не всё так плохо, и компилятор Java можно заставить производить во время проверки типов любые вычисления, лишь бы хватило оперативной памяти. Конкретный способ это сделать был описан в ноябре 2016-го года в этой прекрасной публикации. Его я и хотел бы объяснить.
Для затравки приведу следующий код. Корректен ли он? Предлагаю скомпилировать и проверить, угадали ли вы результат.
Компилятор выбросит java.lang.StackOverflowError независимо от размера стэка.
Разберёмся, почему компилятор ведёт себя именно так (я бы не назвал это багом), как понимание данных причин может быть полезно и причём тут машина Тьюринга.
1. О ковариантности и контравариантности
В первую очередь поговорим об основах. Самый простой способ использования параметризованных типов выглядит примерно так:
Сосредоточимся на контравариантных типах.
2. Формализация подмножества контравариантных типов
Итак, определим, какие именно типы в Java нас интересуют. Введём понятие индуктивно:
Теперь можно наконец ввести отношение является подтипом ««.
В этом месте появляется существенное ограничение. Чтобы отношение совпадало со стандартным способом определения подтипов в Java, необходимо, чтобы в пункте 2 значение n было нечётным.
Полного формального доказательства я приводить не буду, оно было бы неуместно длинным. Правильнее будет рассмотреть ситуацию на примерах.
n=3:
interface S extends C1 >> <>
Докажем, что верно :
Given a generic type declaration
$» data-tex=»inline»/> (n > 0), the direct supertypes of the parameterized type
$» data-tex=»inline»/> where at least one of the
is a wildcard type argument, are the direct supertypes of the parameterized type
$» data-tex=»inline»/> which is the result of applying capture conversion to
$» data-tex=»inline»/> (§5.1.10)
n=2:
interface S extends C1 > <>
Предположим, что :
Случаи n>2 рассматриваются аналогичным образом.
Теперь можно сформулировать следующую теорему, которая позже будет доказана:
Теорема 1
Не существует алгоритма, который для любых двух заданных типови
смог бы определить, является ли верным высказывание
.
Другими словами, в общем случае в Java невозможно определить, является ли один тип подтипом другого.
3. Что будем понимать под машиной Тьюринга
Машина Тьюринга — это пятёрка
, где
— это конечное множество состояний,
— это начальное состояние,
— это конечное состояние,
— это конечный алфавит и
— это функция перехода.
— это дополнительный символ, не содержащийся в
.
Конфигурация машины Тьюринга — это четвёрка , в которой
— это текущее состояние,
— это левая часть ленты,
— это текущий символ и
— это правая часть ленты.
Шаг выполнения машины отображает множество конфигураций само в себя следующим образом:
Так же учитываются граничные случаи (символ здесь означает пустую строку). Они показывают, что по достижении конца строки (слева или справа) к ней автоматически дописывается символ
:
Запуск машины на входе — это последовательность шагов выполнения, начинающаяся с конфигурации
. Если
достигает
, то мы говорим, что машина
завершается (halts) на входе
. Если же функция перехода не позволяет сделать следующий шаг выполнения, будем считать, что машина
ломается на входе
.
4. Subtyping Machines
Начнём связывать воедино имеющиеся у нас понятия. Цель — сопоставить шаги выполнения машины Тьюринга с процессом проверки типов в Java. Положим, что у нас есть такой запрос:
Это утверждение, истинность или ложность которого предлагается доказать. Для удобства введём две альтернативные формы записи:
— это специальная конфигурация, называемая завершающей (halting).
Отметим, что имея правило наследования и подставляя тип
, мы получаем следующее правило выполнения:
Так же в силу контравариантности используемых типов справедливо такое правило:
Используя введённые правила, можно понять, что происходит при проверке типов в примере из начала статьи (они полностью соответствуют алгоритму проверки типов Java на выделенном нами подмножестве контравариантных типов). В нём задано отношение наследования и запрос
.
Цепочка правил выполнения будет следующей:
Как видно, проверка типов зацикливается, этим и обусловлено переполнение стэка во время компиляции. В общем виде описанный процесс можно выразить таким образом:
Выражение
истинно тогда и только тогда, когда существует завершающийся процесс выполнения
.
Пример посложнее
Рассмотрим следующую таблицу классов:
Данный запрос тоже приводит к зацикливанию проверки типов, но теперь это уже нетривиальный цикл. Мы реализовали полноценное блуждание «треугольника» в обе стороны по нашей импровизированной ленте. Убедиться, что проверка типов зацикливается, можно на следующем коде:
5. Построение машины Тьюринга
Имея машину Тьюринга и входную ленту
, построим типы
и
таким образом, что
тогда и только тогда, когда
останавливается на входе
.
Для каждого состояния введём 6 классов:
,
,
,
,
и
; для каждого символа
построим класс
. Символ
из определения машины Тьюринга для удобства будем записывать как
, ему будет соответствовать класс
. Так же дополнительно введём 4 класса:
,
,
и
.
Выглядит немного похоже на последний пример. Дальше будет примерное описание их смысла и конкретный способ эмуляции функции перехода соответствующей машины Тьюринга.
и
— это по сути типы
и
из последнего примера. Большую часть времени они блуждают (wander) вдоль ленты. Смысл типов
и
тоже сохраняется: они нужны для разворота на конце ленты. Единственное исключение — момент, когда
(
это
или
) встречается с соответствующим ему
: он при этом «превращается» в
.
— класс для завершающего состояния, обрабатываемый особым образом.
Полное описание выглядит так:
и
указывают машине, что пришло время для очередного шага выполнения. Соответственно, для каждого правила
в машине Тьюринга
мы строим специальное отношение наследования. При этом не забываем об особых правилах работы с классом
:
Данные отношения выглядят довольно-таки хитро, тем не менее в них можно проследить ряд закономерностей. Механику работы каждого я разбирать не буду, рассмотрим лишь часть. :
:
:
Остальные 9 случаев расписываются аналогичным образом.
6. Fluent interface
Вернёмся в реальный мир. Мы же про Java говорим, а значит наши рассуждения должны в итоге привести к написанию какого-либо кода, желательно полезного.
В мире ООП есть такое понятие, как текучий интерфейс. Вы, возможно, никогда не встречали этого названия, но наверняка видели его реализацию в коде. По сути это просто каскадный вызов методов, использование которого нацелено на повышение читаемости, ну или ещё чего нибудь. Выглядит вот так:
Для этого напишем следующий класс:
Стоит понимать, что тут я описываю только сигнатуру, а не реализации соответствующих методов. О реализации будет позже.
полностью повторяет левую часть требуемого запроса. То есть, следующая строка кода на самом деле запустит требуемую машину Тьюринга во время работы алгоритма проверки типов:
7. Безопасный Builder
Итак, я хочу иметь следующий код, который мог бы валидироваться компилятором:
Требования будут самыми простыми — чтобы оба поля были инициализированы, причём именно в таком порядке и не больше одного раза (я прекрасно понимаю, что такую простую задачу можно решить более подходящими методами; пример с грамматикой посложнее будет позже).
Довольно-таки прямолинейно. Машина остановится только на входе .
Классы User и UserBuilder реализованы следующим образом (осталось только заполнить многоточия):
Осталось только обеспечить требуемое предположение;
Целиком пример можно найти на гитхабе.
Чтобы не быть голословным, далее я привожу пример машины Тьюринга посложнее. Такая машина, грубо говоря, проверяет парность скобок, т.е. выражение ()(()()) является валидным, а выражение ()())(() — невалидным. Только открывающая и закрывающая скобки заменены символами A и B ( x — дополнительный символ, означающий, что скобка на этом месте уже проверена).
Функция перехода будет следующей:
Поиграться с данной машиной, или погенерировать свои, можно всё там же на гитхабе.
Да, генератор кода по описанию машины Тьюринга присутствует.
Для данной грамматики следующий код спокойно скомпилируется:
а вот этот уже нет:
8. Заключение
Содержательная часть на этом закончена. Мы узнали, как можно заставить компилятор валидировать цепочки вызовов согласно произвольному заранее заданному алгоритму.
Но можно — не значит нужно.
Во-первых, слишком много дополнительно объявленных классов, да и сигнатуры методов класса Builder выглядят очень сложно.
Во-вторых, компилятору понадобится гораздо больше памяти, чтобы не падать на сложных выражениях. В первую очередь — гораздо более глубокий стэк.
В-третьих, сложная диагностика ошибок. Типичный вывод компилятора выглядит как-то так (для краткости стёр названия пакетов):
Уровень информативности нулевой. Если хочется найти ошибку, то остаётся только два варианта:
Тогда зачем это всё? Ответов, опять же, несколько:
Разработчики Kotlin, к примеру, знали, что в Java легко составить типы, проверка которых приведёт к экспоненциально долгому времени компиляции, и ввели т.н. Non-Expansive Inheritance Restriction. Поясню на минимальном примере:
Цель проста — избежать «слишком сложных» типов, тем самым гарантируя высокую скорость компиляции. Из-за данного ограничения описанный способ запуска машин Тьюринга на Kotlin реализовать невозможно. В таком случае есть шанс, что проверка типов в Kotlin гарантированно завершается за конечное время.
С другой стороны, если все интерфейсы для машины Тьюринга объявить в Java-файлах, то компилятор Kotlin сделает ровно то же, что и компилятор Java — запустит соответствующую машину. Так что если учесть, что Kotlin используется не в изоляции от Java, то можно заключить, что и его система типов полна по Тьюрингу.