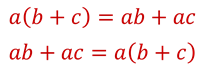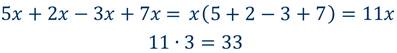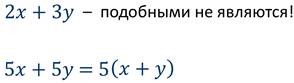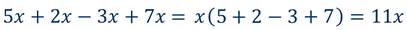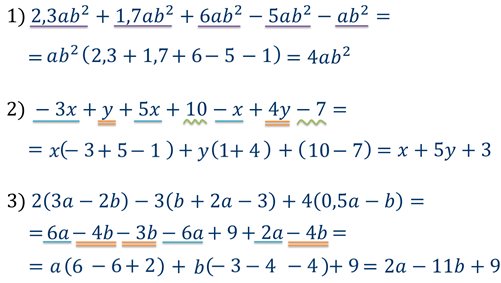Что значит подобные слагаемые 7 класс
Урок по теме «Подобные слагаемые»
Разделы: Математика
Класс: 6
Ключевые слова: подобные слагаемые
Конспект урока математики (урок с использованием case-технологии)
УМК: Математика. 6 класс: учебник для общеобразовательных организаций /Н.Я.Виленкин, В.И.Жохов, А.С.Чесноков, С.И.Шварцбург. 23-е изд.: Просвещение, 2020 год.
Класс: 6
Предмет: математика.
Педагогические технологии: case-технологии, мультимедийные технологии.
Тип урока: урок получения новых знаний.
Цель урока: ввести понятие подобных слагаемых.
Задачи урока:
Планируемые результаты:
Предметные УУД:
Оборудование: мультимедиа, учебник, кейсы с материалом по теме «Подобные слагаемые», сигнальные карточки.
Форма организации деятельности: фронтальная, парная, индивидуальная
Ход урока
1. Мотивация
— На протяжении уже достаточного времени мы с вами работаем с дробями и числами, научились их сравнивать, выполнять. Но мы еще не все знаем про действия с буквенными выражениями. Знания наши пока еще не совсем полные, сегодня узнаем кое-что новое.
2. Актуализация опорных знаний
Урок 42 Бесплатно Подобные слагаемые
В одном из прошлых уроков мы узнали и разобрали одно важное свойство распределительных чисел: распределительное свойство умножения относительно сложения.
Сегодня мы подробно посмотрим, как оно позволяет нам раскрывать скобки и приводить подобные слагаемые, а также в целом упрощать выражение.
Раскрытие скобок
Распределительное свойство умножения справедливо для любых чисел a, b и c.
Также мы уже упоминали, что это свойство можно обобщить, во-первых, для большего числа слагаемых, во-вторых, в роли общего множителей могут выступать не только числа, но и выражения.
Сейчас подробно посмотрим на примерах.
Пример:
Посмотрим на выражение \(\mathbf<(\frac<15><37>+\frac<19><74>)\cdot74>\)
Мы можем сначала посчитать выражение в скобках, а можем сначала раскрыть скобки, избавившись от дробей, а затем выполнить сложение.
Воспользуемся вторым способом:
В данном случае мы имели выражение, максимально близкое к тому, что мы видим в формулировке распределительного свойства.
Теперь рассмотрим такое выражение: \(\mathbf<(1001-65):13>\)
Тут мы видим вычитание вместо сложения и деление вместо умножения.
Но мы уже умеем заменять вычитание на сложение, заменяя вычитаемое на слагаемое, противоположное вычитаемому:
Также и деление мы умеем заменять на умножение, заменяя делитель на множитель, обратный делителю:
Теперь мы получили выражение, соответствующее формулировке распределительного свойства.
Применим же свойство и найдем значение выражения.
Заметим, что хоть мы и заменяли вычитание на сложение, в конце мы все равно вычитали.
Также несмотря на то, что мы заменяли деление на умножение, в конце мы все равно делили.
Распределительное свойство также работает и в таком виде:
Также важно понимать, что распределительное свойство может работать не только с двумя числами, но и с любым другим их количеством.
Три точки обозначают любое количество слагаемых от нуля до бесконечности.
Аналогично предыдущему примеру, слагаемые в скобках могут быть с разными знаками. В таком случае они будут с такими же знаками и в правой части равенства.
Пример:
Раскроем скобки в выражении \(\mathbf<(a+b+c+d)\cdot x>\) :
Также важно понимать, что на месте a, b и других букв в скобках могут стоять любые другие выражения.
Пример:
Также и множитель снаружи скобок может быть не только числом или скобкой, а любым другим выражением, например, как в этом примере ax и bx являются произведениями двух множителей.
Как мы сказали, множитель может быть любым выражением, например, выражением в скобках. Рассмотрим еще такой пример.
Пример:
Раскроем скобки в выражении \(\mathbf<(a+b)(c+d)>\) :
Тут можно действовать в любом порядке: можно считать первую скобку общим множителем, раскрывая вторую, а можно и наоборот.
Мы будем сейчас раскрывать вторую скобку, то есть (\(\mathbf
Теперь общими множителями для первой и второй скобок будут с и d соответственно:
Промежуточный шаг можно было пропустить, так как скобки не несли в нем смысла, но оставим его здесь для наглядности.
Пройти тест и получить оценку можно после входа или регистрации
Вынесение общего множителя
Распределительное свойство умножения относительно сложения помогает нам выносить общий множитель, то есть, смотря на формулировку, мы из правой части переходим в левую.
Сразу скажем, что по аналогии с раскрытием скобок, мы не должны пугаться вычитания и деления, а должны, если сомневаемся, заменять их на сложение и умножение соответственно.
Пример:
Вынесем общий множитель в выражении \(\mathbf
Мы видим, что выражение состоит из трех слагаемых, каждое из которых является произведением.
В каждом из этих произведений есть множитель а.
Его мы и будем выносить.
В данном случае не стояла задача раскрывать скобки. Мы это сделали, чтобы ответ выглядел более законченным
Также можно выносить несколько множителей одновременно.
Пример:
Вынесем общие множители в выражении \(\mathbf
В данном случае в выражении три произведения, в каждом из которых есть множитель а и с, вынесем их:
Кстати, всегда можно проверить себя, раскрыв скобки и убедившись в равенстве полученного выражения и исходного.
Как мы уже сказали, в роли множителей могут выступать всевозможные выражения, а не только числа или произведения. Покажем на примере.
Пример:
Вынесем общие множители в выражении \(\mathbf
Мы видим, что общий множитель есть у первых двух слагаемых и у вторых двух соответственно, вынесем их.
Получается, что выражение состоит из двух слагаемых, каждое из которых является произведением, и в каждом из этих произведений есть множитель \(\mathbf<(a+b>\), вынесем его:
Так мы получили ответ.
Пройти тест и получить оценку можно после входа или регистрации
Приведение подобных слагаемых
В заголовке мы упомянули два новых термина, поэтому сначала дадим им определения.
Подобными слагаемыми называют такие слагаемые, которые имеют одинаковую буквенную часть.
Пример:
Посмотрим, какие есть подобные слагаемые в выражении \(\mathbf<12ab+2b+3ab+5\frac<1><2>b+0.2b>\)
У первого и третьего слагаемого буквенная часть равна \(\mathbf
У второго, четвертого и пятого слагаемого буквенная часть равна \(\mathbf\), эти три слагаемых являются подобными.
Если же мы зададимся вопросом, являются ли подобными первые два слагаемых, то ответ будет отрицательным.
В самом деле, их буквенные части отличаются: \(\mathbf
Внимательный читатель заметит, иногда \(\mathbf
Нередко для удобства подобные слагаемые подчеркивают, причем каждую группу подобных слагаемых подчеркивают разным типом подчеркиваний:
Теперь зная, что такое подобные слагаемые, приступим к их сложению (приведению).
Чтобы привести (сложить) подобные слагаемые, надо сложить их коэффициенты и результат умножить на общую буквенную часть.
Пример:
Возьмем то же выражение и приведем в нем подобные слагаемые.
Как вы видите, процесс очень похож на вынесение общего множителя. В данном случае общим множителем для подобных слагаемых является их одинаковая буквенная часть.
Если мы видим в сумме слагаемое со знаком «минус» перед ним, то и коэффициенты мы будем складывать с этим же знаком.
Пример:
Приведем подобные слагаемые в выражении \(\mathbf<5c+4a-2c+3a>\)
Также достаточно часто встречаются задания вида «раскройте скобки и приведите подобные слагаемые».
Пример:
Раскроем скобки и приведем подобные слагаемые в выражении \(\mathbf<5a(c+3d)-4c(a-d)>\)
В целом, ничего нового в этом задании нет, надо просто аккуратно применить те приемы, которые мы уже освоили.
Пройти тест и получить оценку можно после входа или регистрации
Дополнительная информация
Мы уже говорили про математику в литературе, но речь была про малоизвестные случаи.
Наш урок имеет порядковый номер 42, а это число является крайне популярным в культуре!
Известно оно стало из-за книги Дугласа Адамса «Автостопом по галактике».
В ней сверхразумная раса существ создала мощный компьютер с названием «Думатель» (Deep Thought) с одной лишь целью: найти «Окончательный Ответ на величайший вопрос Жизни, Вселенной и Всего Такого».
После семи с половиной миллионов лет работы компьютер выдал один ответ: число 42.
Дальше отрывок из книги, как отреагировали существа:
“— Сорок два! — взвизгнул Лунккуоол. — И это всё, что ты можешь сказать после семи с половиной миллионов лет работы?
— Я всё очень тщательно проверил, — сказал компьютер, — и со всей определённостью заявляю, что это и есть ответ. Мне кажется, если уж быть с вами абсолютно честным, то всё дело в том, что вы сами не знали, в чём вопрос.
— Но это же великий вопрос! Окончательный вопрос жизни, Вселенной и всего такого! — почти завыл Лунккуоол.
— Да, — сказал компьютер голосом страдальца, просвещающего круглого дурака. — И что же это за вопрос? “
Книга оказалась крайне популярной и читающее сообщество начало гадать, что могло означать это число, какой смысл вкладывал автор.
Но само число стало частью культуры, и, например, в сообществе программистов, часто можно встретить примеры с именно этим числом.
Заключительный тест
Пройти тест и получить оценку можно после входа или регистрации
Повторение: приведение подобных слагаемых
Летняя онлайн-школа по математике задание 17 июля для 6 класса.
Повтори правило приведение подобных слагаемых.
Чтобы привести подобные слагаемые, нужно сложить коэффициенты и результат сложения умножить на буквенную часть.
Реши задание, ответы впиши в форму и отправь на проверку.
Задание: приведи подобные слагаемые
Примеры на приведение подобных слагаемых
Рассмотрим где применяется сложение подобных слагаемых.
Пример 1
Приведите подобные слагаемые: 3х + 15у – 2х – 20у + 7х.
В примере два вида подобных слагаемых, с x и y. Собираем их в разные скобки. Между скобки ставим знак «+».
Пример 2
Приведите подобные слагаемые 3(2k — 4c) — (-6k + c).
Сначала упрощаем выражение: раскрываем скобки, применяя распределительное свойство умножения относительно сложения, и правило раскрытия скобок, перед которыми стоит знак «-» (скобки опускаются, а знаки перед слагаемыми меняются).
3(2k — 4c) — (-6k + c) = 6k — 12c + 6k — c = (6k + 6k) + (- 12c — c) = 12k + (- 13c) = 12k — 13c.
Пример 3
Раскроем скобки и сложим подобные слагаемые.
Пример 4
Решите уравнение 5,4(3y — 2) — 7,2(2y — 3) = 1,2.
Чтобы решить данное уравнение, нужно преобразовать левую часть: раскрыть скобки и привести подобные слагаемые.
5,4(3y — 2) — 7,2(2y — 3) = 1,2;
16,2y — 10,8 — 14,4y + 21,6 = 1,2;
(16,2y — 14,4y) + (21,6 — 10,8) = 1,2;
Переносим 10,8 в правую часть уравнения, изменив знак на противоположный.
y = — 9,6/1,8 = — 96/18 = — 5 6/18 = — 5 1/3.
Приведение подобных слагаемых используется так же и при решении текстовых задач на составление уравнения.
Подобные слагаемые
Урок 42. Математика 6 класс
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Подобные слагаемые»
Сегодня на уроке мы узнаем, какие слагаемые называют подобными, а также научимся приводить подобные слагаемые или, проще говоря, упрощать выражения.
Для изучения нового материала нам понадобятся понятие «коэффициента» и знание распределительного свойства умножения. Вспомним их.
Коэффициентом называют числовой множитель, который записан перед буквенным (одним или несколькими) множителем.
Распределительное свойство умножения справедливо для любых чисел a, b и c.
Оно позволяет, как раскрывать скобки, так и выносить общий множитель за скобки.
Часто при работе с выражениями сначала их обычно упрощают, т.е. преобразуют в более компактную и удобную для вычислений форму.
Найти значение выражения 5х + 2х – 3х + 7х при х = 3.
Конечно, можно просто подставить вместо х указанное значение и посчитать сумму полученных произведений.
Но такой процесс вычислений займёт немало времени. Вычисления значительно упростятся, если обратить внимание, на то, что все слагаемые имеют один и тот же буквенный множитель х. И вот тут к нам на помощь приходит распределительное свойство умножения. Мы знаем, что на основании распределительного свойства можно выносить общий множитель за скобки. Вынесем в нашем выражении общий буквенный множитель х за скобки.
Смотрите, как мы себе упростили вычисления. Такие преобразования можно выполнять только в тех случаях, когда слагаемые имеют одинаковую буквенную часть.
Такие слагаемые называют подобными, а сами преобразования называют приведением подобных слагаемых.
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Замену суммы подобных слагаемых одним слагаемым называют приведением подобных слагаемых.
Подобные слагаемые могут отличаться только коэффициентами. Кроме того, подобными считают и равные слагаемые, а также числа.
Заметим, что слагаемые, у которых равны коэффициенты, а буквенные множители различны, подобными не являются, хотя и к ним иногда полезно применять распределительное свойство умножения.
Ответим на вопрос: зачем же нужно приводить подобные слагаемые?
Ответ на этот вопрос прост. Приводят подобные слагаемые для того, чтобы сделать суммы более короткими, т.е. преобразовывают их в суммы с меньшим числом слагаемых.
Посмотрите, в нашей начальной сумме было 4 слагаемых, а мы её преобразовали в выражение, состоящее из двух множителей. С более короткими суммами легче выполнять вычисления.
Запишем правило, по которому приводят подобные слагаемые:
Для того чтобы привести подобные слагаемые, надо:
1) сложить коэффициенты подобных слагаемых;
2) результат умножить на общую буквенную часть.
Слагаемые, имеющие одинаковую буквенную часть, называют подобными слагаемыми.
Замену суммы подобных слагаемых одним слагаемым называют приведением подобных слагаемых.
Для того чтобы привести подобные слагаемые, надо:
1) сложить коэффициенты подобных слагаемых;
2) результат умножить на общую буквенную часть.
Урок по алгебре в 7 классе «Подобные слагаемые»
Онлайн-конференция
«Современная профориентация педагогов
и родителей, перспективы рынка труда
и особенности личности подростка»
Свидетельство и скидка на обучение каждому участнику
Выбранный для просмотра документ Модель урока в 7классе.docx
Чойна Анна Игоревна, МОУ Лицей №33, учитель математики
Модель урока в 7классе.
Учитель: Чойна Анна Игоревна.
Тема: «Приведение подобных слагаемых».
создать условия для развития у учащихся ключевых компетентностей (социальной, коммуникативной, предметной);
образовательный аспект – создание условий для продолжения формирования умений и навыков составления выражений по условию задачи, а также их преобразование (раскрытие скобок, приведение подобных слагаемых);
личностные: умение понимать смысл поставленной задачи, ясно и четко излагать свои мысли в устной речи; умение работать парами;
предметные: владение навыками преобразования выражений, содержащих подобные слагаемые.
— проектор и доска (экран);
— фотография Краеведческого музея для физкультминутки;
— раздаточный материал для рефлексии;
— жетоны с изображением города;
— интерактивная система голосования Votum ;
Организационный момент (1мин.)
проверка присутствующих на уроке;
настрой учащихся на учебу.
Постановка проблемы (2мин.)
Учитель: А наш урок мы начнем с разгадывания следующего ребуса, который подскажет нам тему урока. Кто догадался, какое словосочетание здесь зашифровано?
Предположительный ответ: Подобные слагаемые.
Учитель: Давайте проверим, правильно ли Вы разгадали ребус.
Учитель: Итак, тема нашего урока: Подобные слагаемые (записываем в тетрадях). А вы знаете определение подобных слагаемых?
Предположительный ответ: Да.
Учитель: Сформулируйте его.
Предположительный ответ: Подобные слагаемые – это слагаемые, у которых буквенная часть одинаковая.
Учитель: Сегодня у нас будет завершающий урок по данной теме. Как Вы думаете, ребята, какую цель мы в связи с этим должны поставить перед собой на этом уроке?
Предположительный ответ: Повторить правила приведения подобных слагаемых в выражениях.
Учитель: С помощью чего мы сможем достигнуть поставленной цели?
Предположительный ответ: Через решение задач.
Учитель: Сегодня у нас будет урок-путешествие, а путешествие мы совершим по знакомым для каждого из Вас местам нашего города. За активную работу, Вы будете получать жетоны с изображением тех мест, о которых мы будем говорить. Тем, у кого в конце урока окажется в руках три жетона получат пятерки, а у кого будет в руках два жетона, получат четверки.
Актуализация знаний (4мин.)
Учитель: Первая остановка под названием «Разминка» у нас будет в киноцентрах нашего города. Администрация попросила помочь нас и посчитать количество кресел во всех киноцентрах вместе, если известно, что КЦ Красном 7х кресел, в КЦ Факеле на 3 кресла меньше, чем в КЦ Красном, в Ю-сити 2х кресла. Давайте составим выражения по условию данной задачи и упростим его. По какому правилу раскрываем скобки, перед которыми стоит знак «+»?
Предположительный ответ: 7х + (7х – 3) + (2х) = 16х – 3.
Учитель: Каков же будет наш ответ администрации города?
Предположительный ответ: В киноцентрах города Комсомольск-на-Амуре всего 16х – 3 кресла. (награждение жетонами)
Закрепление знаний, умений и навыков (22минуты)
Учитель: Далее мы отправляемся в Драматический театр. Чтобы добраться до него, необходимо 40минут ехать на трамвае со скоростью а м/мин, а затем 30минут на автобусе, со скоростью в два раза больше, чем скорость трамвая. Какой путь мы преодолеем? (составление краткой записи по условию задачи)
Предположительный ответ: 40а + 30*2а = 40а + 60а = 100а. (награждение жетонами)
Слайд 5 (работа в парах)
Учитель: Вот мы и прибыли в Драматический театр. Известно, что на представление в пятницу пришло 4 k жителей, в субботу – на 53 человека больше, а в воскресенье – в два раза меньше, чем в пятницу. Сколько человек было на представлениях в Драматическом театре в течение этих трех дней?
Это задание Вам необходимо будет решить вместе со своим соседом. (составление краткой записи по условию задачи)
Правильное решение демонстрируется на экране. Ребята, поднимите руки те, кто правильно справился с этим заданием.
Предположительный ответ: 4 k + (4 k + 53) + (4 k : 2) = 10 k + 53. (награждение жетонами)
Учитель: А чтобы узнать, где будет наша следующая остановка, Вам необходимо найти спрятанные в кабинете части картинки с изображением этого места и составить саму картинку.
Так куда мы отправляемся, ребята?
Предположительный ответ: В краеведческий музей.
Учитель: И следующую остановку мы сделаем в Краеведческом музее. В фондах музея хранится большое количество музейных предметов, из них у археологических коллекций, фотодокументальных коллекций на 46 меньше, а естественнонаучных коллекций в 2 раза больше, чем фотодокументальных. Сколько всего предметов находится в фонде музея?
Предположительный ответ: у + (у – 46) + 2(у – 46) = 4у – 138. (награждение жетонами)
Учитель: Следующую остановку мы с Вами сделаем возле Центральной библиотеки нашего города имени Николая Островского. Здесь Вы можете найти не только интересующую вас книгу, но и посетить различные мероприятия. В библиотеке на данный момент было проведено р литературных вечеров, в 3,5 раза больше творческих встреч, и на 15 презентаций новых книг меньше, чем творческих встреч. На сколько, было больше проведено литературных встреч и творческих встреч, чем презентаций новых книг? (составление краткой записи по условию задачи)
Предположительный ответ: р + (3,5р) – (3,5р – 15) = р + 15. (награждение жетонами)
При хорошей подготовке учащихся и быстром темпе урока возможна дополнительное задание (еще одна остановка).
Учитель: Последнюю остановку мы с Вами сделаем возле еще одного музея нашего города. Как он называется?
Предположительный ответ: Музей изобразительных искусств.
Учитель: Музей изобразительных искусств оказывает разнообразные услуги. В этом месяце было проведено k экскурсий, в 2 раза больше мастер-классов, и на 12 меньше праздников для детей. Сколько всего услуг оказали работники музея в этом месяце?
Предположительный ответ: k + (2 k ) + ( k – 12)=4 k – 12. (награждение жетонами)
Подведение итогов (2мин)
Учитель: Какой теме был посвящен наш урок сегодня?
Предположительный ответ: Приведению подобных слагаемых.
Учитель: Ребята, вспомните цель, которую мы ставили перед собой в начале урока. Смогли ли мы ее достичь с Вами?
Предположительный ответ: Да, мы закрепили навык приведения подобных слагаемых в выражениях.
Учитель: Как Вы думаете, пригодится ли нам умение приводить подобные слагаемые где-то в жизни? Если да, то где?
Предположительный ответ: В строительстве, в кулинарии, в медицине.
Самостоятельная работа (5мин)
Учитель: А теперь настало проверить, насколько каждый из Вас усвоил данную тему. В каждом выражении необходимо привести подобные слагаемые и выбрать правильный вариант ответа.
а ) d + 4a б ) –d + 6a в ) –d – 6a г ) d – 4a
а) 2х – 4 б) 6 в) 2х г) 2х + 4
а) 0 б) 12а + b в) 11а – b г) а – b
а) 4у – 35 б) –4у – 14 в) 14 г) –4у + 14
а) 3 m – 6 k б) m – 2 k в) 3 m – 2 k г) k
Результаты Вы узнаете на следующем уроке.
Учитель: Сейчас каждому из Вас необходимо будет заполнить таблицу под названием «Оцени себя сам».
Понравился ли тебе урок?
Все ли было на уроке тебе понятно?
Научился ли ты составлять выражения по условию задачи?
Можешь ты самостоятельно приводить подобные слагаемые в выражениях?
Активно ли ты работал на уроке?
Как ты считаешь, какую оценку ты заработал на уроке?
Домашнее задание (2мин)
А теперь каждый из Вас должен подсчитать количество завоеванных им жетонов за урок. (выставление оценок за урок)