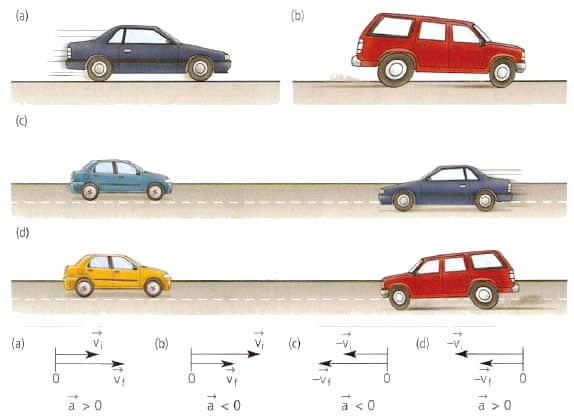
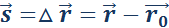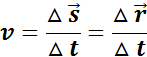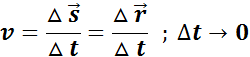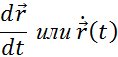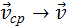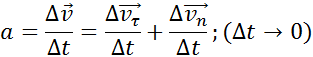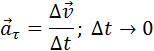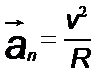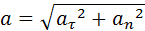Что значит по касательной к траектории

Физика

А Вы уже инвестируете?
Слышали про акцию в подарок?

Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб

План урока:

Закон сложения скоростей

Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена (см. рисунок 1).

Рисунок 1 – Первоначальная скорость пчелы и ветра

Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):

Рисунок 2 – Изменившаяся скорость пчелы

Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v₂ системе отсчета.

Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре

Мгновенная скорость, направление мгновенной скорости

Средняя скорость. Средняя путевая скорость

Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.

Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.

Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:

Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.

То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.

Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt₁, Δt₂,…Δt_n, и найти средние скорости за эти отрезки времени:

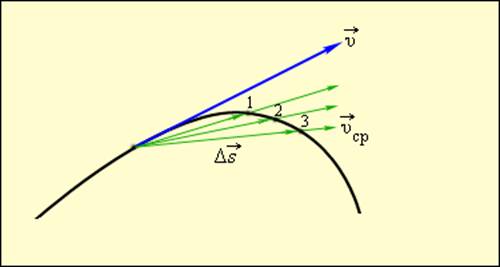
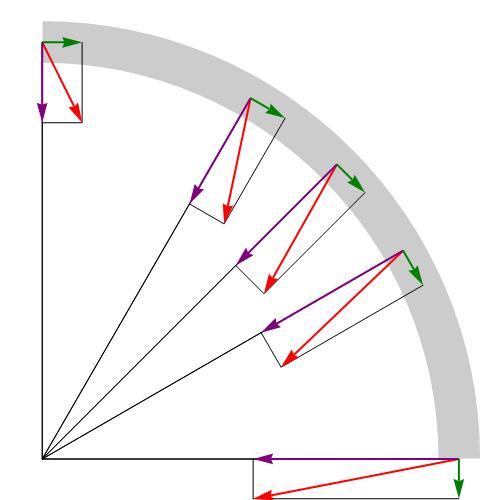
А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δt_b направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.

Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:

Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.

Ускорение. Касательное ускорение. Центростремительное ускорение

Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.

Единицы измерения ускорения:

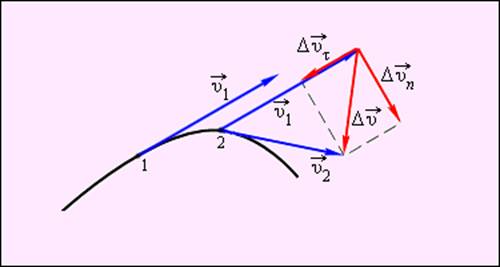
Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)

Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.

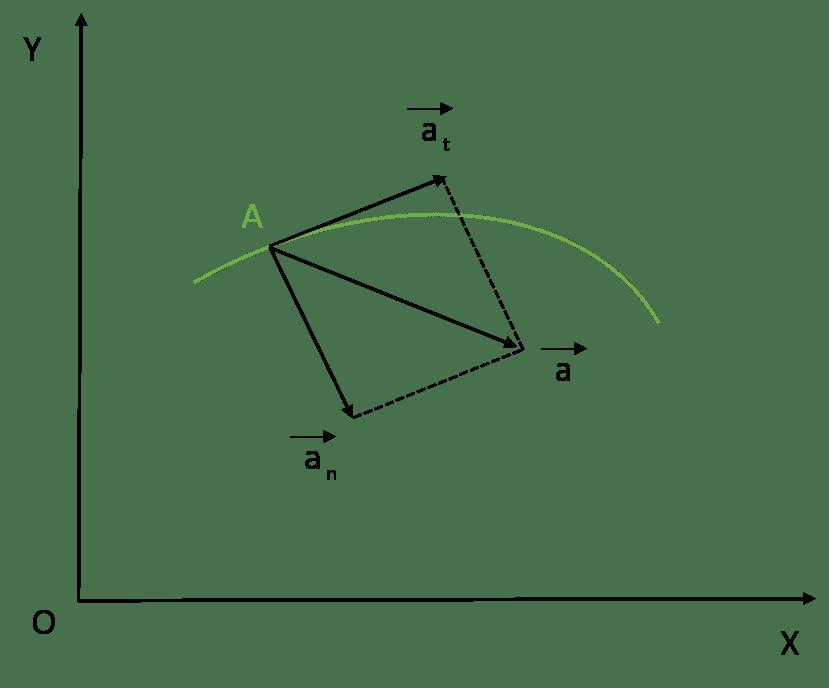
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2

Равноускоренное движение

Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении

Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:

Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.

При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:

Если же ускорение противонаправлено начальной скорости, это выражение станет таким:

Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении

Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.

Свободное падение

Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение

Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.

Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).

Рисунок 9 – Свободное падение тела

Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:

Представим, что тело подкинули вертикально наверх с начальной скоростью v₀ (см. рисунок 10).

Рисунок 10 – Тело бросили вертикально вверх

Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v₀ (вообще нужно было бы писать v_oy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).

Отсюда можно найти полное время полета:

Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.

Рисунок 11 – Тело брошено под углом к горизонту

Уравнения движения в общем виде по двум осям выглядят так:

Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:

Равномерное движение точки по окружности

Центростремительное ускорение

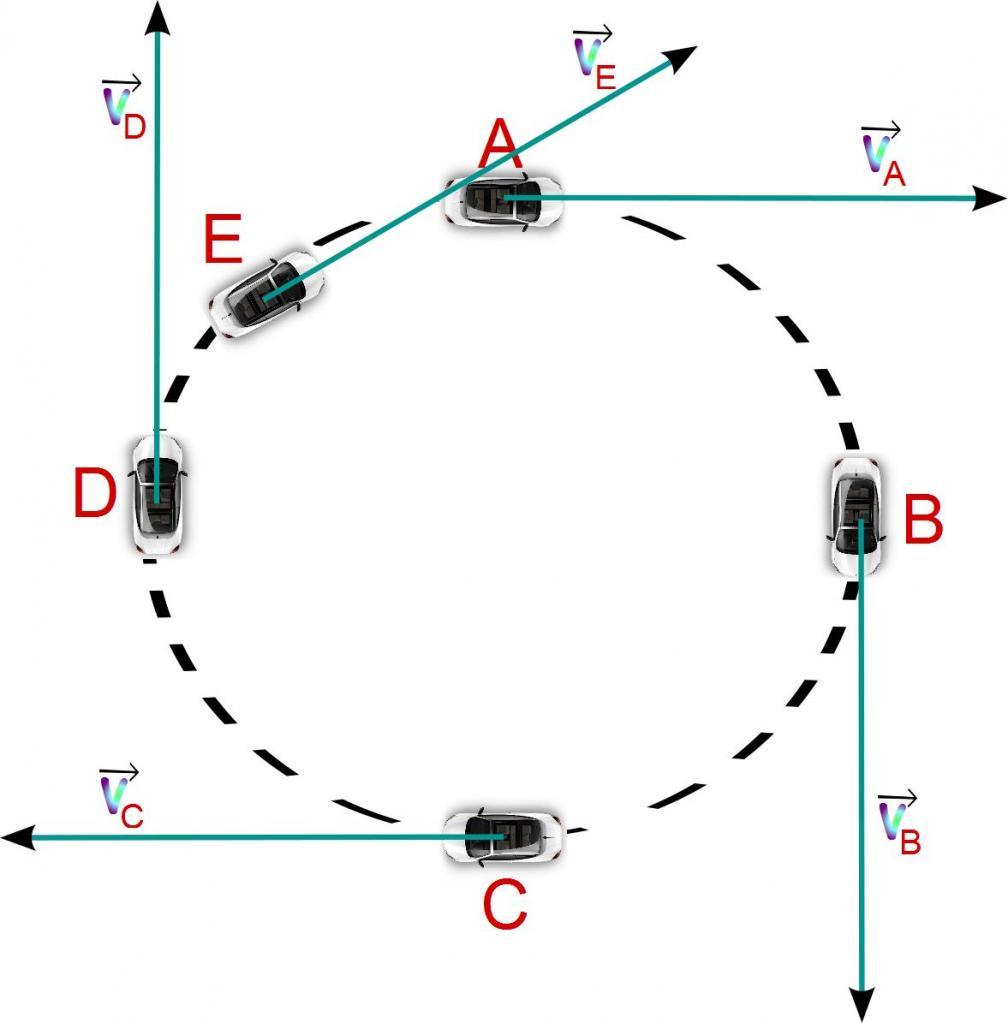
Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).

Рисунок 12 – Изменение направления скорости при равномерном движении по окружности

За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:

где R – радиус окружности, по которой циклически движется тело.

Источник

Основные понятия кинематики

Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин, его вызывающих.

Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.

Механическое движение относительно (см 1.2) Движение одного и того же тела относительно разных тел оказывается различным. Для описания движения тела нужно указать, по отношению к какому телу рассматривается движение. Это тело называют телом отсчета.

Система координат, связанная с телом отсчета, и часы для отсчета времени образуют систему отсчета, позволяющую определять положение движущегося тела в любой момент времени.

В Международной системе единиц (СИ) за единицу длины принят метр, а за единицу времени – секунда.

В системе СГС (Сантиметр, грамм, секунда) приняты соответственно сантиметр и секунда.

Всякое тело имеет определенные размеры. Различные части тела находятся в разных местах пространства. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела.

Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать его материальной точкой. Так можно поступать, например, при изучении движения планет вокруг Солнца.

Если все части тела движутся одинаково, то такое движение называется поступательным. Поступательно движутся, например, кабины в аттракционе «Колесо обозрения», автомобиль на прямолинейном участке пути и т. д. При поступательном движении тела его также можно рассматривать как материальную точку.

Тело, размерами которого в данных условиях можно пренебречь, называется материальной точкой.

Понятие материальной точки играет важную роль в механике.

Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает некоторую линию, которую называют траекторией движения тела.

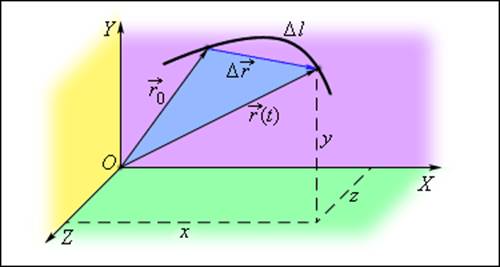
Положение материальной точки в пространстве в любой момент времени (закон движения) можно определять либо с помощью зависимости координат от времени x = x (t), y = 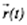y (t), z = z (t) (координатный способ), либо при помощи зависимости от времени

радиус-вектора 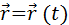(векторный способ), проведенного из

начала координат до данной точки (рис. 1.1.1).

и радиус-вектора

– радиус-вектор положения точки в начальный момент времени

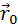
Перемещением тела

называют направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением. Перемещение есть векторная величина.

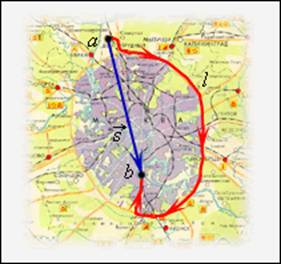
Пройденный путь l равен длине дуги траектории, пройденной телом за некоторое время t. Путь – скалярная величина.

Если движение тела рассматривать в течение достаточно короткого промежутка времени, то вектор перемещения окажется направленным по касательной к траектории в данной точке, а его длина будет равна пройденному пути.

В случае достаточно малого промежутка времени Δt пройденный телом путь Δl почти совпадает с модулем вектора перемещения 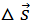При движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути (рис. 1.1.2).

Пройденный путь l и вектор перемещения 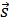при криволинейном движении тела. a и b – начальная и конечная точки пути

Для характеристики движения вводится понятие средней скорости:

В физике наибольший интерес представляет не средняя, а мгновенная скорость, которая определяется как предел, к которому стремится средняя скорость на бесконечно малом промежутке времени Δt,

В математике такой предел называют производной и обозначают

Мгновенная скорость 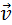тела в любой точке криволинейной траектории направлена по касательной к траектории в этой точке. Различие между средней и мгновенной скоростями показано на рис. 1.1.3.

Средняя и мгновенная скорости.

– перемещения за времена соответственно.

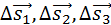
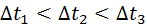
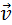
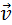
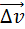
При движении тела по криволинейной траектории его скорость изменяется по модулю и направлению. Изменение вектора скорости за некоторый малый промежуток времени Δt можно задать с помощью вектора (рис. 1.1.4).

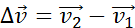
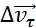
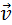
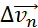
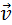
Вектор изменения скорости за малое время Δt можно разложить на две составляющие: направленную вдоль вектора (касательная составляющая), и направленную перпендикулярно вектору (нормальная составляющая).

Изменение вектора скорости по величине и направлению. 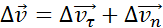– изменение вектора скорости за время Δt

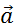
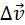
Мгновенным ускорением (или просто ускорением) тела называют предел отношения малого изменения скорости к малому промежутку времени Δt, в течение которого происходило изменение скорости:

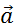
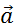
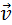
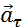
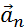
Направление вектора ускорения в случае криволинейного движения не совпадает с направле нием вектора скорости Составляющие вектора ускорения называют касательным (тангенциальным) и нормальным ускорениями (рис. 1.1.5).

Касательное и нормальное ускорения

Касательное ускорение указывает, насколько быстро изменяется скорость тела по модулю:

Вектор 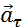направлен по касательной к траектории.

Нормальное ускорение указывает, насколько быстро скорость тела изменяется по направлению.

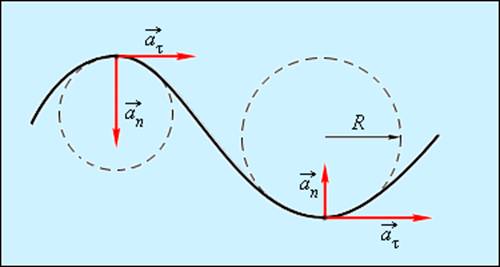
Криволинейное движение можно представить как движение по дугам окружностей (рис. 1.1.6).

Движение по дугам окружностей

Нормальное ускорение зависит от модуля скорости υ и от радиуса R окружности, по дуге которой тело движется в данный момент:

Вектор 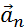всегда направлен к центру окружности.

Из рис. 1.1.5 видно, что модуль полного ускорения равен

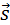
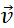
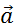
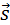
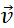
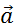
Таким образом, основными физическими величинами в кинематике материальной точки являются пройденный путь l, перемещение , скорость и ускорение . Путь l является скалярной величиной. Перемещение , скорость и ускорение – величины векторные. Чтобы задать векторную величину, нужно задать ее модуль и указать направление. Векторные величины подчиняются определенным математическим правилам. Вектора можно проектировать на координатные оси, их можно складывать, вычитать и т. д.

Источник

Тангенциальное, или касательное ускорение

Все тела, которые окружают нас, находятся в постоянном движении. Перемещение в пространстве тел наблюдается на всех масштабных уровнях, начиная с движения элементарных частиц в атомах вещества и заканчивая ускоренным движением галактик во Вселенной. В любом случае процесс движения происходит с ускорением. В данной статье рассмотрим подробно понятие касательного ускорения и приведем формулу, по которой его можно рассчитать.

Кинематические величины

Прежде чем вести разговор о касательном ускорении, рассмотрим, какими величинами принято характеризовать произвольное механическое перемещение тел в пространстве.

Вам будет интересно: Как научить ребенка делению: основные принципы, простые способы решения и советы учителей

В первую очередь — это путь L. Он показывает, какое расстояние в метрах, сантиметрах, километрах и так далее прошло тело за некоторый промежуток времени.

Вторая важная характеристика в кинематике — это скорость тела. В отличие от пути, она является величиной векторной и направлена вдоль траектории движения тела. Скорость определяет быстроту изменения пространственных координат во времени. Формула для ее вычисления имеет вид:

Вам будет интересно: Как сдать досрочный ЕГЭ?

Наконец, третьей важной характеристикой движения тел является ускорение. Согласно определению в физике, ускорение — это величина, которая определяет изменение скорости от времени. Формулу для него можно записать в виде:

Ускорение, как и скорость, тоже является величиной векторной, однако в отличие от нее оно направлено в сторону изменения скорости. Направление ускорения также совпадает с вектором результирующей силы, оказывающей действие на тело.

Траектория движения и ускорение

Многие задачи в физике рассматривают в рамках прямолинейного движения. В этом случае, как правило, не говорят о касательном ускорении точки, а работают с линейным ускорением. Однако если перемещение тела не является линейным, то полное его ускорение может быть разложено на две составляющие:

В случае линейного движения нормальная составляющая равна нулю, поэтому о векторном разложении ускорения не говорят.

Вам будет интересно: Малоизвестные и интересные факты о золоте

Таким образом, траектория движения во многом определяет характер и составные части полного ускорения. Под траекторией движения понимают воображаемую линию в пространстве, вдоль которой тело перемещается. Любая криволинейная траектория приводит к появлению ненулевых компонент ускорения, отмеченных выше.

Определение тангенциального ускорения

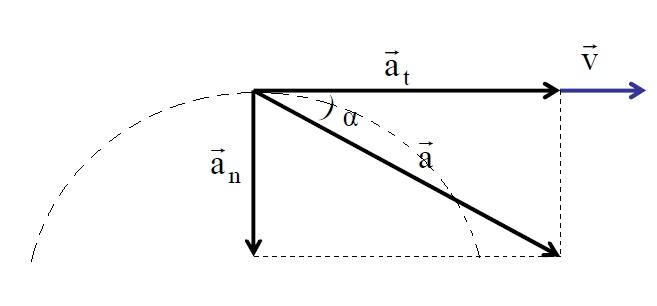
Тангенциальное или, как его еще называют, касательное ускорение — это компонента полного ускорения, которая направлена по касательной к траектории движения. Поскольку вдоль траектории направлена также скорость, то вектор тангенциального ускорения совпадает с вектором скорости.

Получение уравнения касательного ускорения

Предположим, что тело движется по некоторой кривой траектории. Тогда его скорость v¯ в выбранной точке можно представить в следующем виде:

Здесь v — модуль вектора v¯, ut¯ — единичный вектор скорости, направленный по касательной к траектории.

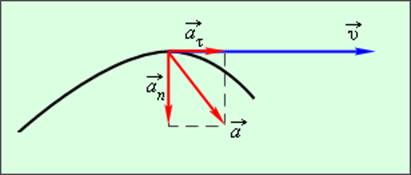
Используя математическое определение ускорения, получаем:

a¯ = dv¯/dt = d(v*ut¯)/dt = dv/dt*ut¯ + v*d(ut¯)/dt

При нахождении производной здесь использовалось свойство произведения двух функций. Мы видим, что полное ускорение a¯ в рассматриваемой точке соответствует сумме двух слагаемых. Они являются касательным и нормальным ускорением точки соответственно.

Скажем пару слов о нормальном ускорении. Оно ответственно за изменение вектора скорости, то есть за изменение направления движения тела вдоль кривой. Если явно вычислить значение второго слагаемого, то получится формула для нормального ускорения:

Нормальное ускорение направлено вдоль нормали, восстановленной в данную точку кривой. В случае движения по окружности нормальное ускорение является центростремительным.

Уравнение касательного ускорения at¯ имеет вид:

Это выражение говорит о том, что тангенциальное ускорение соответствует изменению не направления, а модуля скорости v¯ за момент времени. Поскольку тангенциальное ускорение направлено по касательной к рассматриваемой точки траектории, то оно всегда перпендикулярно нормальной компоненте.

Тангенциальное ускорение и модуль полного ускорения

Выше была представлена вся информация, которая позволяет вычислить полное ускорение через касательное и нормальное. Действительно, так как обе компоненты являются взаимно перпендикулярными, то их вектора образуют катеты прямоугольного треугольника, гипотенузой которого является вектор полного ускорения. Этот факт позволяет записать формулу для модуля полного ускорения в следующем виде:

Угол θ между полным ускорением и тангенциальным можно определить так:

Чем больше тангенциальное ускорение, тем ближе оказываются направления касательного и полного ускорения.

Связь касательного и углового ускорения

Типичной криволинейной траекторией, по которой движутся тела в технике и природе, является окружность. Действительно, перемещение шестерен, лопастей и планет вокруг собственной оси или вокруг своих светил происходит именно по окружности. Движение, соответствующее этой траектории, называется вращением.

Кинематика вращения характеризуется теми же величинами, что кинематика движения по прямой, однако, они имеют угловой характер. Так, для описания вращения используют центральный угол поворота θ, угловые скорость ω и ускорение α. Для этих величин справедливы следующие формулы:

Предположим, что тело совершило один оборот вокруг оси вращения за время t, тогда для скорости угловой можно записать:

Линейная скорость в этом случае будет равна:

Теперь вычислим производную по времени от левой и правой частей равенства, получим:

Таким образом, тангенциальное ускорение и аналогичная угловая величина связаны равенством:

Если предположить, что вращается диск, то тангенциальное ускорение точки при постоянной величине α будет возрастать линейно с увеличением расстояния от этой точки до оси вращения r.

Далее, решим две задачи на применение записанных выше формул.

Определение тангенциального ускорения по известной функции скорости

Известно, что скорость тела, которое перемещается по некоторой кривой траектории, описывается следующей функцией от времени:

Необходимо определить формулу касательного ускорения и найти его значение в момент времени t = 5 секунд.

Сначала запишем формулу для модуля тангенциального ускорения:

То есть для вычисления функции at(t) следует определить производную скорости по времени. Имеем:

at = d(2*t2 + 3*t + 5)/dt = 4*t + 3

Подставляя в полученное выражение время t = 5 секунд, приходим к ответу: at = 23 м/с2.

Задача на определение тангенциального ускорения

Известно, что материальная точка начала равноускоренное вращение с нулевого момента времени. Через 10 секунд после начала вращения ее центростремительное ускорение стало равным 20 м/с2. Необходимо определить касательное ускорение точки через 10 секунд, если известно, что радиус вращения равен 1 метр.

Сначала запишем формулу для центростремительного или нормального ускорения ac:

Пользуясь формулой связи между линейной и угловой скоростью, получим:

При равноускоренном движении скорость с угловым ускорением связаны формулой:

Подставляя ω в равенство для ac, получим:

Линейное ускорение через тангенциальное выражается так:

Подставляем последнее равенство в предпоследнее, получаем:

ac = at2/r2*t2*r = at2/r*t2 =>

Последняя формула с учетом данных из условия задачи приводит к ответу: at = 0,447 м/с2.

Источник